300iq Contest 1
链接
F. Free Edges
水题，一定只留下一棵森林对应的边不删
B. Best Subsequence
考虑正难则反，从后往前删。
这样取一个位置 \(i\)，要求 \(a_i+a_{R[i]}\) 最大，然后删掉 \(i\) 和 \(R[i]\) 中较大的那个。
考虑如果不删 \(i,R[i]\) 中的任何一个，显然答案就是 \(a_i+a_{R[i]}\)，删别的没有用。而无论删掉两个之中的哪一个，序列其他位置都不会变化，那么相同条件下，显然越小越好。
用链表维护左右位置，复杂度 \(O(n\log n)\)。
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#define N 200010
using namespace std;
int a[N],L[N],R[N];
struct node{
int u,v,w;
node(int U=0,int V=0,int W=0):u(U),v(V),w(W){}
bool operator <(const node a)const{return w<a.w;}
};
priority_queue<node>q;
void push(int x){q.push(node(x,R[x],a[x]+a[R[x]]));}
bool cut[N];
int get()
{
while(!q.empty())
{
node x=q.top();q.pop();
if(!cut[x.u] && !cut[x.v]) return a[x.u]>a[x.v]?x.u:x.v;
}
throw;
}
void del(int x){cut[x]=true;L[R[x]]=L[x];R[L[x]]=R[x];push(L[x]);}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++) R[i]=i+1,L[i]=i-1;
L[1]=n;R[n]=1;
for(int i=1;i<=n;i++) push(i);
while(m<n) ++m,del(get());
int u=get();
printf("%d\n",max(a[u]+a[R[u]],a[u]+a[L[u]]));
return 0;
}
C. Cool Pairs
构造题。考虑实际上我们可以钦定一个数组 \(a\) 的权值，不妨假设从小到大依次是 \(i-1\)。
这样对于数组 \(b\)，如果选 \(-n\) 那么贡献为 \(n-i\)，如果选 \(0\) 那么贡献为 \(0\)。
可以发现至多只有一个位置不是 \(-n\) 或 \(0\)。假设这个位置是 \(i\)，那么此时要求的值已经小于 \(n-i\) 了，那么大力取出后面的 \(a_i\) 排个序即可。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 300010
#define ll long long
using namespace std;
int n;ll m;
int p[N];int q[N];
int a[N],b[N],c[N],cc;
int main()
{
scanf("%d%lld",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&p[i]);
for(int i=1;i<=n;i++) scanf("%d",&q[i]);
puts("Yes");
for(int i=1;i<=n;i++) b[q[i]]=i-1;
for(int i=1;i<=n;i++)
{
int x=n-p[i];
if(m==0) a[p[i]]=n;
else if(m>=x) m-=x,a[p[i]]=-n;
else
{
for(int j=p[i]+1;j<=n;j++) c[++cc]=b[j];
sort(c+1,c+cc+1);
a[p[i]]=-c[m+1];
m=0;
}
}
for(int i=1;i<=n;i++) printf("%d ",a[i]);puts("");
for(int i=1;i<=n;i++) printf("%d ",b[i]);puts("");
return 0;
}
D. Dates
首先有一个结论，就是不断从大往小加，如果加入后不合法就跳过。考虑简易证明就是如果冲突了，那么删掉较小的那个效果和删掉较大的那个是一样的。
考虑 Hall 定理，可以发现一个区间集合是合法的当且仅当任取其中的一个子集，其包含的点数不小于集合大小。考虑这道题里面选的一定是一个区间，所以题意变成不存在一组区间 \((l,r)\) 使得区间个数 \(r-l+1\) 大于区间长度即 \(r\) 的右端点到 \(l\) 的左端点范围内的 \(a_i\) 和。
考虑这样即找到一组 \((a,b)\)，使得 \(\text{ind}_a-\text{ind}_b\leq r_a-l_b\)。即 \(\text{ind}_a-r_a\leq \text{ind}_b-l_b\)。
而 \(\text{ind}\) 即编号，每次加入一个数字只会导致一个后缀的点发生变化，故直接线段树维护 \(\text{ind}_a-r_a\) 极大值和 \(\text{ind}_a-l_a\) 极小值，插入时查询左右部分是否符合条件即可。复杂度 \(O(n\log n)\)。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<functional>
#define N 300010
#define inf 10000000000000000
#define ll long long
using namespace std;
int l[N],r[N],w[N],id[N];
ll s[N];int a[N],n;
struct seg_tree{
function<ll(ll,ll)> f;
ll val[N<<2],tag[N<<2];
void upd(int x){val[x]=f(val[x<<1],val[x<<1|1]);}
void set(int x,int v){val[x]+=v;tag[x]+=v;}
void push(int x){if(tag[x]) set(x<<1,tag[x]),set(x<<1|1,tag[x]),tag[x]=0;}
void build(int u,int l,int r,int a[])
{
if(l==r){val[u]=-s[a[l]];return;}
int mid=(l+r)>>1;
build(u<<1,l,mid,a);build(u<<1|1,mid+1,r,a);
upd(u);
}
void insert(int u,int l,int r,int L,int R,int v)
{
if(L>R) return;
if(L<=l && r<=R){set(u,v);return;}
int mid=(l+r)>>1;push(u);
if(L<=mid) insert(u<<1,l,mid,L,R,v);
if(R>mid) insert(u<<1|1,mid+1,r,L,R,v);
upd(u);
}
ll qry(int u,int l,int r,int L,int R)
{
if(L<=l && r<=R) return val[u];
int mid=(l+r)>>1;push(u);
if(L>mid) return qry(u<<1|1,mid+1,r,L,R);
if(R<=mid) return qry(u<<1,l,mid,L,R);
return f(qry(u<<1,l,mid,L,R),qry(u<<1|1,mid+1,r,L,R));
}
}t1,t2;
int main()
{
int t;
scanf("%d%d",&n,&t);
for(int i=1;i<=t;i++) scanf("%d",&a[i]),s[i]=s[i-1]+a[i];
for(int i=1;i<=n;i++) scanf("%d%d%d",&l[i],&r[i],&w[i]),id[i]=i,--l[i];
sort(id+1,id+n+1,[&](int x,int y){return w[x]>w[y];});
t1.f=[&](ll x,ll y){return min(x,y);};
t2.f=[&](ll x,ll y){return max(x,y);};
t1.build(1,1,n,l);t2.build(1,1,n,r);
ll ans=0;
for(int _=1;_<=n;_++)
{
int u=id[_];
if(t1.qry(1,1,n,1,u)<t2.qry(1,1,n,u,n)+1) continue;
ans+=w[u];
t2.insert(1,1,n,u,n,1);t1.insert(1,1,n,u+1,n,1);
}
printf("%lld\n",ans);
return 0;
}
K. Knowledge
XJ 搬过的题。
一个合理的猜想是，任何一个串都可以通过若干次操作之后变成一个很短的串。即尝试找到若干等价类，其实这就是群。
可以把 \(a\)，\(b\) 看成两种操作，使得 \(aa,bbb,ababab\) 操作后得到的东西不变，即这是三条轨道。其实这是一个经典的四面体群，可以构造一个有两种不同颜色的四面体：
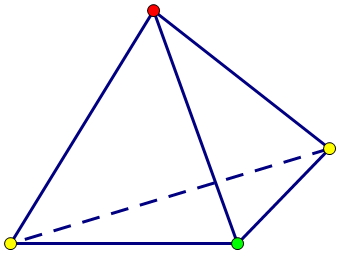
三种操作（\(2a,3b,3ab\)）对应三条轨道。
所以总共只有 12 种状态，且最简的长度均 \(< 6\)，爆搜完打个表即可。
然后考虑处理读入的字符串的对应状态，这个可以直接暴力将所有长度为 \(6\) 的字符串转化为其最简长度。
然后放矩阵快速幂上处理即可。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<bitset>
#include<map>
#define mod 998244353
#define N 200010
using namespace std;
string s;
#define M 12
struct matrix{
int a[M+2][M+2];
int* operator [](int b){return a[b];}
matrix(){memset(a,0,sizeof(a));}
friend matrix operator *(matrix a,matrix b)
{
matrix c;
for(int i=0;i<M;i++)
for(int k=0;k<M;k++)
for(int j=0;j<M;j++) c[i][j]=(c[i][j]+1ll*a[i][k]*b[k][j])%mod;
return c;
}
}a,r;
matrix ksm(matrix a,int k)
{
matrix o;for(int i=0;i<M;i++) o[i][i]=1;
for(;k;k>>=1)
{
if(k&1) o=o*a;
a=a*a;
}
return o;
}
string B[]={"","a","b","ab","ba","bb","aba","bab","abb","bba","babb","bbab"};
string U[]={"aa","abab","abba","baba","babba","bbaba","bbabb","bbb"};
string V[]={"","bba","bab","abb","bbab","babb","aba",""};
map<string,int>id;
map<string,string>nxt;
int base(string s)
{
string u="";
for(int i=0;i<s.size();i++)
{
u+=s[i];
for(int j=u.size()-1;j>=max((int)u.size()-5,0);j--)
if(nxt.count(u.substr(j,u.size())))
{
string v=nxt[u.substr(j,u.size())];
u.erase(j);u+=v;break;
}
}
return id[u];
}
int main()
{
for(int i=0;i<12;i++) id[B[i]]=i;
for(int i=0;i<8;i++) nxt[U[i]]=V[i];
int n,m;
cin>>m>>s>>n;
base(s);
int u=base(s);
for(int i=0;i<12;i++) a[i][base(B[i]+"a")]=a[i][base(B[i]+"b")]=1;
r=ksm(a,n);
printf("%d\n",r[0][u]);
return 0;
}
H. Hall's Theorem
考虑最方便的情况显然是任意两个点的连边之间互相为子集关系。
我们让所有点排个序，那么一个点集的连边集合就是最大标号的连边数。
钦定第 \(i\) 个位置的边，如果它钦定了 \(j\) 条边，那么左边任选 \(j-1\) 个点都合法。
直接贪心取，复杂度 \(O(n^2)\)。
#include<iostream>
#include<cstdio>
#include<cstring>
#define N 30
using namespace std;
int n,k;
int tt,ax[N*N],ay[N*N];
void add(int x,int y){++tt;ax[tt]=x;ay[tt]=y;}
int C[N][N];
int main()
{
scanf("%d%d",&n,&k);
C[0][0]=1;
for(int i=1;i<=n;i++)
for(int j=C[i][0]=1;j<=n;j++) C[i][j]=C[i-1][j]+C[i-1][j-1];
k=(1<<n)-1-k;
int p=n;
for(int i=n;i;i--)
{
for(int j=1;j<=p;j++)
if(C[i-1][j-1]>k) break;
else k-=C[i-1][j-1],add(i,j);
}
printf("%d\n",tt);
for(int i=1;i<=tt;i++) printf("%d %d\n",ax[i],ay[i]);
return 0;
}
E. Expected Value
神仙题。
显然有一个 \(O(n^3)\) 的高斯消元做法。
考虑平面图有什么性质：它的边数是 \(O(n)\) 级别的，所以这是一张稀疏图。事实上这也是这道题平面图唯一要用到的性质。
直接掏出一个 \(O(nm)\) 的行列式，暴力解出 \(x_1\) 即可。具体参考 zzq 论文。
当然这道题也可以不用这么暴力。考虑大胆猜测一下：用 \(f_i\) 表示 \(i\) 步走到 \(n\) 的概率，那么最后的 \(f_i\) 一定构成一个整式递推。事实上根据各种定理，可以证明递推长度也是 \(O(n)\) 的。
大力 BM 求出长度为 \(m\) 的递推式 \(g_i\)，那么有 \(\forall i\geq m\ ,\ f_i=\sum_{j< m} f_{i-j-1}g_j\)，看着很像多项式卷积？事实上构造生成函数，就有 \(F(x)=F(x)G(x)-F_0(x)\)，移项得 \(F(x)=\frac{-F_0(x)}{1-G(x)}\)。
我们要求的是 \(\sum_{i}if_i\)，实际上对应就是 \(F'(1)\)。根据除法求导有 \(F(1)=\frac{A(1)}{B(1)}\)，\(F'(1)=\frac{A'(1)B(1)-A(1)B'(1)}{B^2(1)}\)。
直接暴力求导就好了。复杂度 \(O(n^2)\)。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#define N 3010
#define M N*3
#define S(a) ((int)a.size())
#define R(a,n) (a.resize(n))
#define pb push_back
#define il inline
#define mod 998244353
using namespace std;
typedef vector<int> poly;
int nxt[M<<1],to[M<<1],head[N],cnt;
int deg[N];
void adde(int u,int v)
{
nxt[++cnt]=head[u];
to[cnt]=v;head[u]=cnt;
++deg[u];
}
il int add(int x,int y){return x+y>=mod?x+y-mod:x+y;}
il int dec(int x,int y){return x-y<0?x-y+mod:x-y;}
int ksm(int a,int b=mod-2)
{
int r=1;
for(;b;b>>=1,a=1ll*a*a%mod) if(b&1) r=1ll*r*a%mod;
return r;
}
poly operator +(const poly a,const poly b)
{
poly c=S(a)>S(b)?a:b;
for(int i=0;i<min(S(a),S(b));i++) c[i]=add(a[i],b[i]);
return c;
}
poly operator *(const poly a,const poly b)
{
poly c(S(a)+S(b)-1);
for(int i=0;i<S(a);i++)
for(int j=0;j<S(b);j++) c[i]=add(c[i],1ll*a[i]*b[i]%mod);
return c;
}
namespace BM{
poly g[M];int d[M];
int fail[M];
poly work(int f[],int n)
{
int cnt=0,mn=0;
for(int i=0;i<=n;i++)
{
d[i]=0;
for(int j=1;j<=S(g[cnt]);j++) d[i]=add(d[i],1ll*f[i-j]*g[cnt][j-1]%mod);
d[i]=dec(d[i],f[i]);
if(!d[i]) continue;
fail[cnt]=i;
if(!cnt){g[++cnt]=poly(i+1);continue;}
int t=fail[mn],w=1ll*d[i]*ksm(d[t])%mod;
poly c(i-t-1);
c.pb(w);
for(int v:g[mn]) c.pb(1ll*v*(mod-w)%mod);
g[cnt+1]=g[cnt]+c;
if(i-t+S(g[mn])>=S(g[cnt])) mn=cnt;
++cnt;
}
return g[cnt];
}
}
using BM::work;
int iv[N],f[M],p[M],p0[M];
int main()
{
iv[1]=1;
for(int i=2;i<=N-5;i++) iv[i]=1ll*(mod-mod/i)*iv[mod%i]%mod;
int n,m;
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%*d%*d");
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
adde(u,v),adde(v,u);
}
p[1]=1;f[0]=0;
int T=n*3;
for(int i=1;i<=T;i++)
{
for(int u=1;u<n;u++)
for(int j=head[u];j;j=nxt[j])
p0[to[j]]=add(p0[to[j]],1ll*p[u]*iv[deg[u]]%mod);
for(int j=1;j<=n;j++) p[j]=p0[j],p0[j]=0;
f[i]=p[n];
}
poly g=work(f,T);
poly p(S(g)),q(S(g)+1);
q[0]=1;
// for(int i=0;i<S(g);i++) printf("%d ",f[i]);puts("");
// for(int i=0;i<S(g);i++) printf("%d ",g[i]);puts("");
for(int i=0;i<S(g);i++)
{
p[i]=f[i];
for(int j=1;j<i;j++) p[i]=dec(p[i],1ll*f[i-j]*g[j-1]%mod);
q[i+1]=mod-g[i];
}
int p0=0,p1=0,q0=0,q1=0;
for(int i=0;i<S(p);i++) p0=add(p0,p[i]);
for(int i=0;i<S(q);i++) q0=add(q0,q[i]);
for(int i=0;i<S(p);i++) p1=add(p1,1ll*i*p[i]%mod);
for(int i=0;i<S(q);i++) q1=add(q1,1ll*i*q[i]%mod);
printf("%lld",((1ll*p1*q0-1ll*p0*q1)%mod+mod)*ksm(1ll*q0*q0%mod)%mod);
return 0;
}
A. Angle Beats
看到题面就感觉一脸匹配的样子。
考虑一个 \(\text{+}\) 可以从四周的 \(\text{·}\) 中选两个组成匹配。一个 \(\text{*}\) 可以从上下选一个 \(\text{·}\)，左右选一个 \(\text{·}\) 组成匹配。
考虑一个经典的处理方式，就是将一个 \(\text{+}\) 拆开，然后两点之间连边，每个点再向四周的点连边，这样如果这个点要选择，必然会拆掉之间的点边，然后连两条周围的边。
对于 \(\text{*}\) 同理，不过一个连上下一个连左右。这样处理之后就是一个一般图最大匹配问题，直接带花树 \(O(nm\alpha(n))\) 冲过去就好了。事实上带花树和匈牙利一样，根本跑不满，常数小到离谱。
最后输出方案挺阴间的。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
const int N=110;
int n,m;
vector<int>g[N*N*2];
namespace flower_tree{
const int N=20010;
queue<int>q;
int col[N],f[N];
int find(int x){return f[x]==x?f[x]:(f[x]=find(f[x]));}
int pre[N],lik[N];//pre:增广路 , lik:匹配
int T,vis[N];
int lca(int x,int y)
{
for(x=find(x),y=find(y),++T;vis[x]!=T;)
{
vis[x]=T;
x=find(pre[lik[x]]);
if(y) swap(x,y);
}
return x;
}
void flower(int x,int y,int v)
{
for(;find(x)!=v;x=pre[y])
{
pre[x]=y;y=lik[x];
if(col[y]==2) col[y]=1,q.push(y);
if(f[x]==x) f[x]=v;if(f[y]==y) f[y]=v;
}
}
void clear(int n)
{
while(!q.empty()) q.pop();
for(int i=1;i<=n;i++) f[i]=i,pre[i]=col[i]=0;
}
bool dfs(int s,int n)
{
clear(n);
col[s]=1;q.push(s);
while(!q.empty())
{
int u=q.front();q.pop();
for(int v:g[u])
if(find(u)!=find(v) && col[v]!=2)
{
if(col[v])
{
int w=lca(u,v);
// if(w==0) throw;
flower(u,v,w);flower(v,u,w);
continue;
}
col[v]=2;pre[v]=u;
if(lik[v]) col[lik[v]]=1,q.push(lik[v]);
else
{
for(int x=v,y=lik[pre[x]];x;x=y,y=lik[pre[x]])
lik[x]=pre[x],lik[pre[x]]=x;
return true;
}
}
}
return false;
}
}
using flower_tree::dfs;
using flower_tree::lik;
int id[N][N],cnt;
char s[N][N];
const int ux[]={0,1,0,-1},uy[]={1,0,-1,0};
void add(int x,int y){g[x].push_back(y);g[y].push_back(x);}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%s",s[i]+1);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(s[i][j]=='.')
{
bool hv=false;
for(int t=0;t<4;t++)
if(s[i+ux[t]][j+uy[t]]=='+' || s[i+ux[t]][j+uy[t]]=='*') hv=true;
if(hv) id[i][j]=++cnt;
}
else
{
int hv=0;
for(int t=0;t<4;t++)
if(s[i+ux[t]][j+uy[t]]=='.') hv++;
if(hv>=2) id[i][j]=++cnt,cnt++;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(id[i][j] && s[i][j]!='.')
{
add(id[i][j],id[i][j]+1);
if(s[i][j]=='*')
{
if(s[i-1][j]=='.') add(id[i-1][j],id[i][j]);
if(s[i+1][j]=='.') add(id[i+1][j],id[i][j]);
if(s[i][j-1]=='.') add(id[i][j-1],id[i][j]+1);
if(s[i][j+1]=='.') add(id[i][j+1],id[i][j]+1);
}
else
{
for(int t=0;t<4;t++)
if(s[i+ux[t]][j+uy[t]]=='.')
add(id[i+ux[t]][j+uy[t]],id[i][j]),add(id[i+ux[t]][j+uy[t]],id[i][j]+1);
}
}
for(int i=1;i<=cnt;i++)
if(!lik[i]) dfs(i,cnt);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(id[i][j] && (s[i][j]=='*' || s[i][j]=='+'))
{
if(lik[id[i][j]]==id[i][j]+1) continue;
static bool hv[26];
memset(hv,0,sizeof(hv));
int u1=lik[id[i][j]],u2=lik[id[i][j]+1];
if(!u1 || !u2) continue;
for(int t=0;t<4;t++)
{
int x=i+ux[t],y=j+uy[t];
if(id[x][y]==u1 || id[x][y]==u2)
{
for(int p=0;p<4;p++)
if(s[x+ux[p]][y+uy[p]]>='a' && s[x+ux[p]][y+uy[p]]<='z')
hv[s[x+ux[p]][y+uy[p]]-'a']=true;
}
if(s[x][y]>='a' && s[x][y]<='z') hv[s[x][y]-'a']=true;
}
char c='a';
while(hv[c-'a']) c++;
s[i][j]=c;
for(int t=0;t<4;t++)
{
int x=i+ux[t],y=j+uy[t];
if(id[x][y]==u1 || id[x][y]==u2) s[x][y]=c;
}
}
for(int i=1;i<=n;i++,puts(""))
for(int j=1;j<=m;j++) putchar(s[i][j]);
return 0;
}
J. Jealous Split
首先题目要求的东西实际上就是对于任意两个区间，将他们任意相邻的部分划到另一个区间不会导致他们差的绝对值变小。
我们考虑构造一个函数使得它满足这个性质。由于权值非负，有 \((a+b)^2+c^2< a^2+(b+c)^2 \Leftrightarrow a< c\) 我们不妨用一个区间的平方表示这个区间的权值。
可以发现这样最终答案等价于使得选出的区间权值平方之和尽可能小。
要恰好选 \(k\) 个区间，可以联想到 wqs 二分。而权值平方和又可以想到斜率优化。但是这里要输出方案，wqs 二分不一定能行。
但是考虑每次斜率优化的同时维护一个切点所在的区间，转移时每次转移到上一个可以成为答案的区间即可。复杂度 \(O(n\log^2 n)\)。
除此之外还有一种直接构造的 \(O(n\log n)\) 做法，没看懂。
#include<iostream>
#include<cstdio>
#include<cstring>
#define N 100010
using namespace std;
typedef long long ll;
int n,k,a[N];
ll s[N],f[N];
struct node{
ll x,y;
node(ll X=0,ll Y=0):x(X),y(Y){}
}p[N];
node operator -(node a,node b){return node(a.x-b.x,a.y-b.y);}
long double operator *(node a,node b){return 1.0L*a.x*b.y-1.0L*a.y*b.x;}
bool cmp(int a,int b,int c){return (p[b]-p[a])*(p[b]-p[c])>=0;}
ll sum(int l,int r){return f[l]+(s[r]-s[l])*(s[r]-s[l]);}
int q[N],ql,qr;
int cl[N],cr[N];
int L[N],R[N];
void solve(ll x)
{
#define now q[ql]
#define pre q[ql-1]
#define nxt q[ql+1]
ql=qr=1;q[ql]=0;
for(int i=1;i<=n;i++)
{
while(ql<qr && sum(now,i)>sum(nxt,i)) ql++;
if(ql==1 || sum(now,i)!=sum(pre,i))
cl[now]=L[now],cr[now]=R[now];
for(;ql<qr && sum(now,i)==sum(nxt,i);ql++)
cl[nxt]=min(L[nxt],cl[now]),cr[nxt]=max(R[nxt],cr[now]);
L[i]=cl[now]+1,R[i]=cr[now]+1;
f[i]=sum(now,i)+x;
p[i]=node(s[i],s[i]*s[i]+f[i]);
while(ql<qr && cmp(q[qr-1],q[qr],i)) --qr;
q[++qr]=i;
}
}
int ans[N];
int main()
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),s[i]=s[i-1]+a[i];
ll l=0,r=s[n]*s[n]+1,res=0;
while(l<=r)
{
ll mid=(l+r)>>1;
solve(mid);
if(L[n]<=k && k<=R[n]){res=mid;break;}
if(R[n]>=k) l=mid+1;
else r=mid-1;
}
int u=n;
for(int i=n-1,j=k-1;i;i--)
if(L[i]<=j && j<=R[i] && sum(i,u)+res==f[u]) ans[j]=u=i,j--;
puts("Yes");
for(int i=1;i<k;i++) printf("%d ",ans[i]);
return 0;
}
G. Graph Counting
神仙题。
考虑什么样的图才会成为“好”的图。
\[ {塔特-伯格公式}\\
图 G 的匹配数=\frac 12\min_{U\subseteq V}\{|U|-\text{odd}(G-U)+|V|\}
\]
考虑我们要让图 \(G\) 没有完美匹配，就要让 \(\exists\ U\subseteq V\ ,\ |U|<\text{odd}(G-U)\) 而且任意加一条边都变得合法。首先如果加边在 \(|U|\) 上那么仍然不合法，所以这里的 \(U\) 中点必须向其他点连满。
然后考虑加边在 \(G-U\) 中，如果存在偶大小的联通块那么一定不合法。所以所有 \(G-U\) 的联通块一定为奇数。而如果一个联通子图可以继续连边，那么连边后可以不改变 \(\text{odd}(G-U)\)，所以所有联通子图必须没有边。
那么这样如果 \(|U|=x\)，那么剩下的图就是由 \(x+1\) 或 \(x+2\) 个大小为奇数的团构成。根据点数是偶数显然不存在 \(x+1\) 个奇团，所以只有 \(x+2\) 个奇团。
等同于问 \(2n-x\) 个点分成 \(x+2\) 个奇团的方案数。由于是奇团，考虑 \(-1\) 再 \(/2\)，那么等于问 \(n-x-1\) 分成 \(x+2\) 份的方案数。
考虑等同于 \(\sum_{x=2}^{n+1}S(n-x+1)\)，其中 \(S(x)\) 表示 \(x\) 的拆分数。那么 \(x\) 实际上枚举了拆分的层数，去掉一步拆完的情况，即 \(S(n+1)-1\)。
直接用五边形数多项式求逆。
\[\phi(x)=\prod_{i\geq 1}(1-x^i)
\\
\phi(x)=1+\sum_{i=1}^{+\infty}(-1)^ix^{\frac{i(3i±1)}{2}}
\\
F(x)=\prod_{i\geq 1}\sum_{j\geq 0}x^{ij}=\frac{1}{\prod_{i\geq 1}(1-x^i)}=\frac{1}{\phi(x)}
\]
复杂度 \(O(n\log n)\)。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#define S(a) ((int)a.size())
#define R(a,n) (a.resize(n))
#define P(...) poly({__VA_ARGS__})
#define il inline
using namespace std;
const int N=500010,mod=998244353;
typedef long long ll;
typedef vector<int> poly;
il int mul(int x,int y){return 1ll*x*y%mod;}
il int add(int x,int y){return x+y>=mod?x+y-mod:x+y;}
il int dec(int x,int y){return x-y<0?x-y+mod:x-y;}
int ksm(int a,int b=mod-2)
{
int r=1;
for(;b;b>>=1,a=1ll*a*a%mod) if(b&1) r=1ll*r*a%mod;
return r;
}
poly operator +(poly a,poly b)
{
int m=max(S(a),S(b));R(a,m);R(b,m);
poly c(m);
for(int i=0;i<m;i++) c[i]=add(a[i],b[i]);
return c;
}
poly operator -(poly a,poly b)
{
int m=max(S(a),S(b));R(a,m);R(b,m);
poly c(m);
for(int i=0;i<m;i++) c[i]=dec(a[i],b[i]);
return c;
}
namespace NTT{
const int G=3,Gi=(mod+1)/G;
int rev[N<<2];
int get_rev(int n)
{
int lim=1,l=0;
for(;lim<=n;lim<<=1) l++;
for(int i=1;i<lim;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
return lim;
}
void ntt(poly &f,int lim,int op=1)
{
for(int i=0;i<lim;i++) if(i<rev[i]) swap(f[i],f[rev[i]]);
for(int mid=1;mid<lim;mid<<=1)
{
int r=ksm(op==1?G:Gi,(mod-1)/(mid*2));
for(int i=0;i<lim;i+=mid<<1)
for(int j=0,o=1;j<mid;j++,o=mul(o,r))
{
int x=f[i+j],y=mul(o,f[i+j+mid]);
f[i+j]=add(x,y);f[i+j+mid]=dec(x,y);
}
}
if(op==-1) for(int i=0,r=ksm(lim);i<lim;i++) f[i]=mul(f[i],r);
}
}
using NTT::get_rev;using NTT::ntt;
poly Set(poly a,int n){if(n>S(a)){R(a,n);return a;}else return poly(a.begin(),a.begin()+n);}
poly operator *(poly a,poly b)
{
int n=S(a)+S(b)-1;
if(min(S(a),S(b))<=5)
{
poly c(n);
for(int i=0;i<S(a);i++)
for(int j=0;j<S(b);j++) c[i+j]=add(c[i+j],1ll*a[i]*b[j]%mod);
return c;
}
int lim=get_rev(n);
R(a,lim);R(b,lim);
ntt(a,lim);ntt(b,lim);
for(int i=0;i<lim;i++) a[i]=mul(a[i],b[i]);
ntt(a,lim,-1);
return Set(a,n);
}
poly Inv(poly a)
{
if(S(a)==1) return P(ksm(a[0]));
int m=(S(a)+1)>>1;
poly b=Inv(Set(a,m));
return Set((P(2)-a*b)*b,S(a));
}
int n;
int main()
{
scanf("%d",&n);++n;
poly a(n+1);
a[0]=1;
for(int i=1;i*(3*i-1)/2<=n;i++)
{
if(i*(3*i-1)/2<=n) a[i*(3*i-1)/2]=i&1?mod-1:1;
if(i*(3*i+1)/2<=n) a[i*(3*i+1)/2]=i&1?mod-1:1;
}
a=Inv(a);
printf("%d\n",dec(a[n],1));
return 0;
}
I. Interesting Graph
考虑题目给的条件等同于每个联通块大小不超过 \(6\)（否则任意取相邻的七个点就不合法）可以直接状压求出联通块的色多项式。事实上根据各种递推公式，色多项式的系数应该是 \(O(n)\) 的。
而不同联通块之间显然没有联系，直接卷积即可。事实上由于 \(6\) 个点的不同构的图实际上是极少的，大概不到 \(100\) 个，直接拎出来跑一遍背包即可。
复杂度 \(O(n\times\text{玄学})\)。
代码咕咕咕了
本文来自博客园，作者：Flying2018，转载请注明原文链接：https://www.cnblogs.com/Flying2018/p/14725252.html
