wqs二分&闵可夫斯基和学习笔记

关于 wqs 二分部分可以参考跳蛙的博客或者原论文，基础部分这里略过。

wqs 二分的构造解

wqs 二分的本质是二分斜率，寻找切点。假设希望求出值的横坐标为 \(X\)。但是事实上由于三点共线情况的存在，切点横坐标不一定恰好等于 \(X\)。

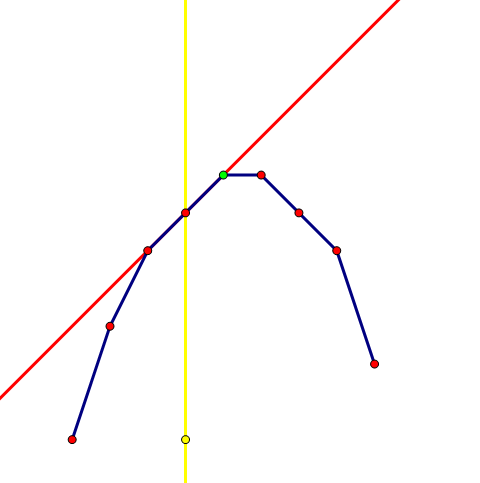
红线是切线，黄线是 \(x=X\)，而 wqs 二分求出的切点可能是绿点。

不过对于一般的 wqs 二分问题，只要知道切线的截距和斜率，可以很容易求出任何切线上的点的坐标。但是有些情况下需要进行构造，上述做法就不太行了。

一种方法是随机扰动，这种方法在出题人精心构造的情况下复杂度会退化为指数级。

我们需要一种不导致复杂度退化的方法。显然的一点是，任意一条切线切在凸包上的点，其横坐标一定构成一个区间。而我们知道，只要最终 \(X\) 落在这个区间内，那么一定存在至少一组解。

显然对于 wqs 二分能处理的大部分问题，其 dp 过程中的答案仍然是凸的。实际上对于序列问题，我们 dp 的就是每一个前缀的切点，每个切点的坐标是由前面的切点转移过来的。

那么现在所以对于每一个 dp 的子问题，我们都记录切线所切的区间。这样我们可以从最后开始，每次尝试找到上一个可行的转移点（可行指的是 \(X\) 要落在其切点的区间内）。

当然，我们大可以不必转移整个区间。既然我们已经知道了它是一个区间，那么我们直接转移其最大值与最小值即可：

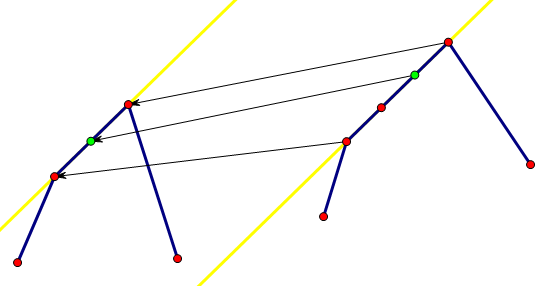
如上图，红点对应的转移可以直接求出，由此可以推出绿点（要求的解）的转移。

不妨用 \(L_i,R_i\) 记录第 \(i\) 个凸包的切线区间，那么我们只需要找到 \(X\in[L_j,R_j]\) 并且可以转移当前位置的 \(j\) 即可。

Gym102268J Jealous Split

转化后题意：构造一组方案，将长度为 \(n\) 的序列 \(a_i\) 分割为恰好 \(k\) 段非空的子区间，最小化 \(\displaystyle\sum_{i\leq k}\left(\sum_{j=l_i}^{r_i}a_j\right)^2\)。

使用上述做法就可以构造出一组可行解。

当然这道题还有另一种构造的方法，但是与本文无关。

wqs 二分与费用流

事实上要严格证明一个函数是凸的需要不少时间，比如经典的 wqs 二分问题：

给定长度为 \(n\) 序列 \(a_i\)，要求选择恰好 \(k\) 个不相交的非空子区间，使得选中元素的价值和最大。

其实直接证明它的凸性并不容易，或者说并没有那么显然。

但是我们知道的一点是，费用流模型的函数一定是凸的。这里费用流函数 \(F(x)\) 指的是钦定源点 \(S\) 向汇点 \(T\) 流恰好 \(x\) 的流量下的最小费用。

也就是说，如果我们能够将上述问题建出流量为 \(k\) 费用流模型，那么自然证明了答案关于 \(k\) 是凸的。

而上述问题很容易建出费用流模型：

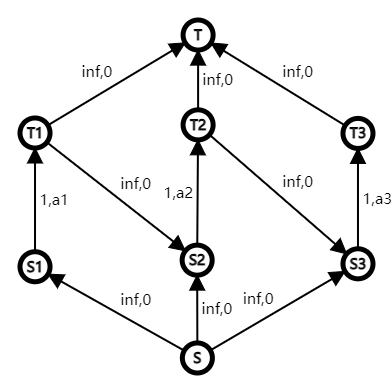
自然就证明了答案是一个凸性的函数。

事实上，大部分 wqs 二分的问题都可以建出费用流模型（当然复杂度不一定正确）。

举个例子：

[八省联考2018]林克卡特树

事实上这题相当于点有限流，每次可以流任意一条简单路径。

那费用流模型也很显然，直接将每个点拆成入点和出点，一条树边对应出点向入点连边。类似于上图的形式（不过扩展到了树上而已）

然后源点向每个点，每个点向汇点分别连 \((\inf,0)\) 表示可以任选两个点作为起点终点。

然后就可以套上 wqs 二分了，之后 dp 内容不是本文重点。

闵可夫斯基和

标准定义：

\[C=\{a+b|a\in A,b\in B\} \]

似乎有 \(|C|=|A||B|\) ？但是实际上我们需要的只是 \(C\) 点集的外层凸包，可以证明一定有 \(|C|\leq |A|+|B|\)。

举个例子：

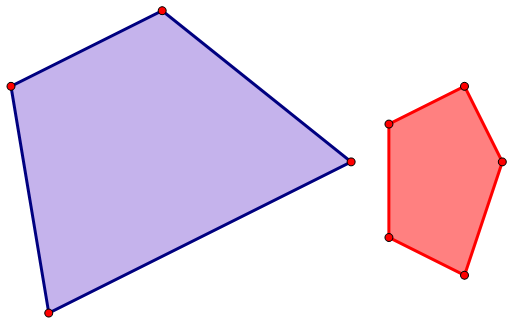
需要将上述两个凸包做闵可夫斯基和。可以直接将其中一个凸包的每个顶点换成另一个凸包，然后保留外层凸包：

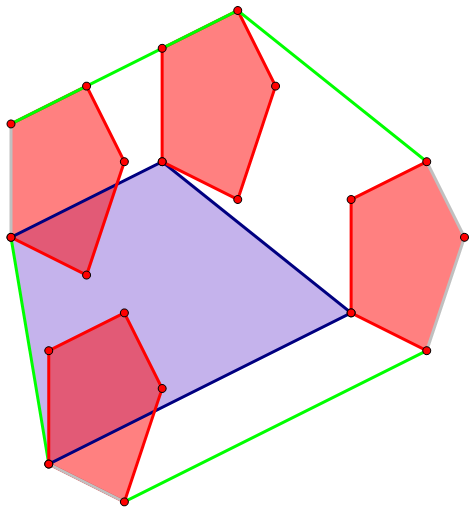
可以发现凸包上只有 \(8\) 个点（不算共线的情况）。

事实上可以证明的是，从一个凸包跳到另一个凸包的线（即绿色部分）至多只有 \(|A|\) 条，凸包内部转移的线（灰色部分）至多只有 \(|B|\) 条。

下凸壳闵可夫斯基和

下凸壳就是凸包留下下半部分的点集，可以看成被下方平行光照射到的部分。

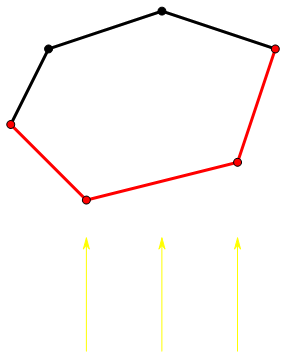
下凸壳闵可夫斯基和当然可以仿照凸包的写法。但是这里有一个更方便的写法：

考虑下凸壳的一个性质：即任意 \(x\) 坐标至多对应一个点。

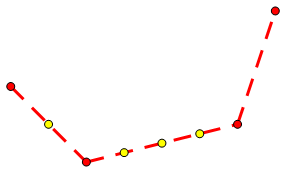
把这些点全部描述出来，我们完全可以用一个 \(O(\text{值域})\) 的数组记录这些点值，这样就不必描述边的信息。比如上述的凸包可以用 \(\{2,1,0,\frac 14,\frac 12,\frac 34,1,3\}\) 表示。

如果我们求出它的差分数组，由于原数组是一个凸包，所以是单调不降的。

考虑求闵可夫斯基和的过程，本质上就是将两个差分数组归并排序一下。

演示：

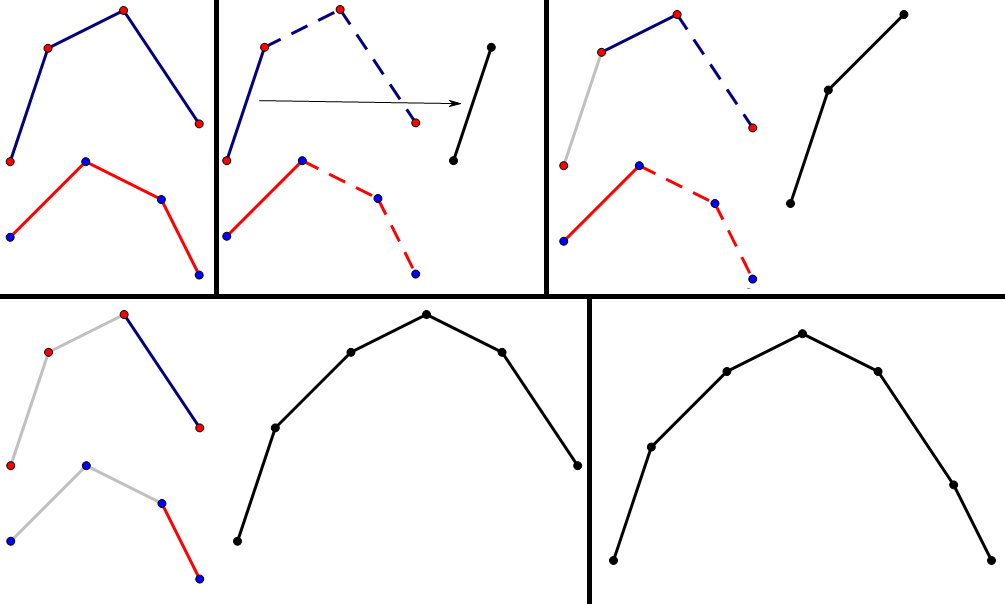
当然我们并不需要真的求出差分数组，可以直接用两个指针指向需要合并的凸包，每次将斜率较大的点加入新的凸包即可。复杂度 \(O(|A|+|B|)\)。

代码十分简洁：

#define S(a) ((int)a.size())
typedef long long ll;
typedef vector<ll> vec;
vec operator +(const vec &a,const vec &b)
{
    if(!S(a) || !S(b)) return vec();
    vec c;c.reserve(S(a)+S(b));
    c.push_back(a[0]+b[0]);
    int p=1,q=1;ll w=a[0]+b[0];
    while(p<S(a) || q<S(b))
    {
        if(q>=S(b) || (p<S(a) && a[p-1]-a[p]>b[q-1]-b[q])) c.push_back(w+=a[p]-a[p-1]),p++;
        else c.push_back(w+=b[q]-b[q-1]),q++;
    }
    return c;
}

同样，通过这种记录的方式也可以很容易处理下凸壳的和（即两个下凸壳的并）。由于我们已经证明了取并后结果一定是一个下凸壳，故直接将每个 \(x\) 轴对应的位置取 \(\min\) 即可。

闵可夫斯基和与 wqs 二分

可以观察到，wqs 二分的函数图像一定是一个上凸壳/下凸壳，而横坐标的值域 \(k\) 通常等于点数，故可以用上述记录每个 \(x\) 对应点值的方式记录。

观察朴素的 dp 转移方程，其中 \(j\)（即记录选了多少条边）一维必然直接相加，即有 \(H(i+j)=\max(F(i)+G(j))\)，可以发现这恰好对应上述的闵可夫斯基和与上/下凸包求并。与 wqs 二分不同的是，这样维护出来的凸包实际上对于每一个 \(x\in[0,n]\) 都求出了答案。

处理多次询问

如果将上面那道 wqs 二分的题目改成多组询问，即：

给定长度为 \(n\) 序列 \(a_i\)，要求对于每个 \(k\in[1,n]\) ，求出恰好选 \(k\) 个不相交的非空子区间，最大化选中元素的价值和。

这样 wqs 二分就不太可做了，考虑用闵可夫斯基和处理。

具体来说，先考虑一种 naive 的 dp：令 \(f _ {l,r,k,0/1,0/1}\) 表示区间 \(l,r\) 选 \(k\) 个，其中左端点有/无区间覆盖，右端点有/无区间覆盖。

为什么要加上后两维呢？因为我们处理区间合并的时候其实是可以合并中间的区间的，即：

\[f _ {l,r,i+j-1,x,y}\leftarrow f _ {l,p,i,x,1}+ f _ {p+1,r,j,1,y} \]

直接这样做当然是 \(O(n^3)\) 的。但是如果我们把上述 dp 写成 \(f _ {l,r,0/1,0/1}(k)\) 的函数形式，可以发现这一定是一个凸函数。

所以我们任取一个 \(p\in[l,r)\)，都可以在 \(O(r-l)\) 的时间用闵可夫斯基和求出函数。这恰好就是归并排序的复杂度分析。

所以仿照归并排序的思想，我们取 \(p=\lfloor\frac{l+r}2\rfloor\)，就可以在 \(O(n\log n)\) 内对所有 \(k\in[0,n]\) 求出答案。

Gym102331J Jiry Matchings

题意

给定一颗大小为 \(n\) 的树，边有边权表示匹配的价值。问对于 \(k\in[1,n]\) 求出恰好 \(k\) 匹配的价值之和最大值。无解输出 \(\text{?}\)。

题解

既然是匹配，显然可以转化为费用流模型，故答案关于 \(k\) 的凸性显然。

考虑如果只对某一个 \(k\) 求答案怎么做。由于是答案是凸的，故可以套用 wqs 二分，二分每多选一个匹配的额外价值 \(w\)，然后用 \(f_{i,0/1}\) 表示 \(i\) 子树中任意匹配的最大价值，其中 \(i\) 选/不选。转移显然。

那么对于所有 \(k\) 求，显然的想法就是闵可夫斯基和，但是有一个问题是，闵可夫斯基和是 \(O(|A|+|B|)\) 而不是被合并集合大小，意味着它并不能套用启发式合并的思路。

考虑仿照树上背包分治NTT 做法，我们对原树轻重链剖分，然后对于轻链直接暴力合并，复杂度 \(O(siz)\)。

对于重链，先合并所有轻链的结果，然后做同上面那道题的分治处理，复杂度 \(O(siz\log siz)\)。其中在每次重链处理中，子树内的点会被合并 \(O(\log n)\) 次，一个点到根有 \(O(\log n)\) 条轻链，故总复杂度 \(O(n\log^2 n)\)。

事实上仿照树上背包分治NTT 的思路按权分治做到 \(O(n\log n)\)。具体来说合并的时候找到一个分治点使得两边凸包大小之和尽量接近，这样每次重链合并凸包大小至少 \(\times 1.5\)，复杂度 \(O(n\log_{1.5} n)\)。

关键代码：

void dfs1(int u,int p)
{
    fa[u]=p;siz[u]=1;
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i];
        if(v==p) continue;
        fw[v]=w[i];
        dfs1(v,u);siz[u]+=siz[v];
        if(siz[v]>siz[son[u]]) son[u]=v;
    }
}
struct matr{
    vec g[2][2];//g[0/1][0/1]：左边/右边 是否强制不匹配
    //g[0][x]>=g[1][x] , g[x][0]>=g[x][1]
    vec* operator [](int a){return g[a];}
    matr(){}
    matr(int u){g[0][0]=f[u][0];g[0][1]=g[1][0]=f[u][1];}
};
matr merge(const matr &a,const matr &b,int w)
{
    matr c;
    For01(X) For01(x) For01(y) For01(Y)
    if(x && y) c[X][Y]=max(c[X][Y],inc(a.g[X][x]+b.g[y][Y],1,w));
    else c[X][Y]=max(c[X][Y],a.g[X][x]+b.g[y][Y]);
    return c;
}
matr solve(int l,int r,vec &g)
{
    if(l==r) return matr(g[l]);
    int s=0,mid=l;
    for(int i=l;i<=r;i++) s+=f[g[i]][0].size();
    int w=f[g[l]][0].size();
    while(mid<r-1 && w*2<=s) w+=f[g[++mid]][0].size();
    return merge(solve(l,mid,g),solve(mid+1,r,g),fw[g[mid]]);
}
vec g[N];
void dfs2(int u,int top)
{
    f[u][0].pb(0);f[u][1].pb(0);
    for(int i=head[u];i;i=nxt[i])
    {
        int v=to[i];
        if(v==son[u] || v==fa[u]) continue;
        dfs2(v,v);
    }
    if(u==1) return;
    if(son[u]) dfs2(son[u],top);
    g[top].push_back(u);
    if(u!=top) return;
    auto s=solve(0,S(g[top])-1,g[top]);
    int p=fa[u];
    f[p][0]=max(f[p][0]+s[0][0],inc(f[p][1]+s[0][1],1,fw[u]));
    f[p][1]=f[p][1]+s[0][0];
    g[top].clear();f[u][0].clear();f[u][1].clear();
}

处理区间询问

Gym102331H Honorable Mention

题意

给定长度为 \(n\) 序列 \(a_i\)，\(q\) 次询问 \([l_i,r_i,k_i]\)，求出 \([l_i,r_i]\) 中选恰好选 \(k_i\) 个不相交的非空子区间，选中元素的价值和的最大值。

题解

~~没想到吧居然是同一场比赛的~~。

考虑线段树分治，然后保留分治过程每一个子区间的凸包。

一个显然的想法是得到每次询问的 \(O(\log n)\) 个区间，将每个区间当成一个物品，即在上面花费 \(k\) 个区间会得到 \(w_k\) 的价值。

由于最后的答案是凸的，故可以 wqs 二分额外价值 \(w\)，然后在每个区间上二分切点。复杂度 \(O(q\log^2 n\log V)\)（二分答案+线段树分治+二分切点），由于区间左右端点的覆盖状态还需要枚举，算法自带 \(16\) 倍大常数，难以通过。

可以发现的是，线段树上总点数只有 \(O(n\log n)\) 个，而总询问次数却有 \(O(q\log^2 n)\) 次，可以发现二分答案十分浪费。

假如每次询问的斜率 \(w\) 是单调递增的，那么可以直接在每个凸包上维护一个指针，暴力移动到切点的位置，这样总复杂度等于总点数即 \(O(n\log n)\)。

那么一个优化就是询问离线，然后找到每个询问需要查询的斜率，按该斜率排序，每一次 reset 凸包的指针位置，每次查询仿照上述均摊的做法。

总二分次数是 \(O(\log V)\)，故指针移动总次数 \(O(n\log n\log V)\)，总询问次数 \(O(q\log n\log V)\)，排序复杂度 \(O(q\log q\log V)\)。

总时间复杂度 \(O((q+n)\log n\log V)\)。