如何建一个SAM
部分改编自OI WIKI
先从一个简单的问题入手:
给定一个串,构造一个图,使其能够表示它的所有子串。
显然一个子串就是一个后缀的前缀。所以一个很显然的方式就是把所有后缀扔进trie里。
比如当前串是aaba。

但是我们发现,这样是不是有点浪费?比如"ba"这个字符串好像在里面出现了三遍。
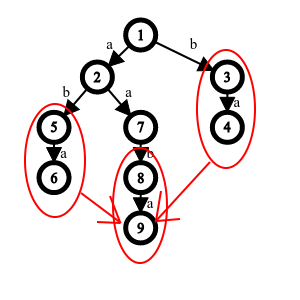
既然树型结构已经不能更优了,那么我们不妨另辟蹊径,考虑能不能找到一个算法,用一个DAG代替这个trie树。比如将上述三个红色圆圈合并,可以变成:
.png)
答案是肯定的。这个算法就是SAM。
先在这里展示一些简单的字符串的后缀自动机。
这里用蓝色表示初始状态,用绿色表示终止状态。
对于字符串 \(s=\varnothing\) :
对于字符串 \(s=\texttt{a}\):
对于字符串 \(s=\texttt{aa}\):
对于字符串 \(s=\texttt{ab}\):
对于字符串 \(s=\texttt{abb}\):
对于字符串 \(s=\texttt{abbb}\):
看起来有点复杂?那么我们该如何建这样一个后缀自动机呢?
这里先给出结论:我们可以在 \(O(n)\) 时间内建出这样的后缀自动机而且代码极短。
在建后缀自动机之前,我们需要先了解一下一些性质:
我们定义 \(\operatorname{endpos}(t)\) 为母字符串 \(s\) 的非空子串 \(t\) 在字符串 \(s\) 中的所有结束位置的集合。
例如 s="\(\texttt{aabab}\)",t="\(\texttt{ab}\)",那么 \(\operatorname{endpos}(t)=\{2,4\}\)。
关于endpos集合的性质 OI WIKI 讲的很详细。但是有点繁琐。这里给出我的理解:
根据endpos集合我们可以一个树形关系,其中根结点为 \(\varnothing\),每个节点的endpos集合都完全包含其儿子的endpos集合。且对于两个没有祖先关系的点,endpos交为 \(\varnothing\)。
事实上这个树形关系就是parent树。这在后面会用到。
关于证明详见 OI WIKI。
可以发现,对于SAM的某个节点 \(u\),其表示的字符串是 \(s\) 长度为 \(len_u\) 的前缀中长度大于某一长度的后缀。而 \(len_u\) 显然也是 \(u\) 表示的子串中最长的那个。
可以证明,\(len_u\) 等于它插入时的字符串的长度。
我们考虑记 \(\operatorname{link}(u)=v\) 为最长的 \(len_v\) 使 \(\operatorname{endpos}(u)\subseteq\operatorname{endpos}(v)\)。
那么 \(u\) 表示的字符串是 \(s\) 长度为 \(len_u\) 的前缀中长度大于 \(len_{\operatorname{link}(u)}\) 的后缀。
证明详见 OI WIKI。
例如当s="\(\texttt{abcbc}\)"时,SAM和parent树如下所示:
接下来我们可以开始建SAM了。
先放一个板子:
void insert(int c)
{
int p=las,q=las=++cnt;
len[q]=len[p]+1;
for(;p && !ch[p][c];p=fa[p]) ch[p][c]=q;
if(!p) fa[q]=1;
else
{
int np=ch[p][c];
if(len[np]==len[p]+1) fa[q]=np;
else
{
int nq=++cnt;
memcpy(ch[nq],ch[np],sizeof(ch[nq]));
fa[nq]=fa[np];
fa[np]=fa[q]=nq;
len[nq]=len[p]+1;
for(;p && ch[p][c]==np;p=fa[p]) ch[p][c]=nq;
}
}
}
首先需要注意一点,这里的 \(\text{fa}\) 本质上其实是 \(\text{link}\),即并不存在fa[ch[u][c]]=u之类的关系。
我们一步步解释这段程序在干什么。
int p=las,q=las=++cnt;
len[q]=len[p]+1;
for(;p && !ch[p][c];p=fa[p]) ch[p][c]=q;
\(las\) 是我们上一次插入的节点,而 \(q\) 是我们要加入的节点。
如果我们记 \(s_u\) 表示节点 \(u\) 能表示的最长的子串,那么 \(s_q=s_{p}+c\)。
所以显然有 len[q]=len[p]+1。接下来我们要给 \(q\) 找 \(fa\)。
接下来个人感觉特别像KMP,即我们知道 \(s_{fa[p]}\) 一定是 \(s_p\) 的一个后缀。我们希望找到一个已经存在的状态,它存在一个 \(c\) 边的扩展。
如果不存在当前 \(p\) 不存在 \(c\) 边的扩展,那么显然 \(q\) 本身就是一个新的扩展,直接赋值 ch[p][c]=q,然后继续向上找。
if(!p) fa[q]=1;
else
{
int np=ch[p][c];
if(len[np]==len[p]+1) fa[q]=np;
如果找到根了还是没有找到 \(c\) 边的扩展,说明当前串不存在前驱,那么我们直接令 fa[q]=1。
否则我们找到了一个 \(c\) 边的扩展,显然这是存在 \(c\) 边的扩展中最长的子串。接下来判断这个扩展是不是直接的,即是 \(s_{np}=s_p+c\) 还是 \(s_{np}=s_p+c\dots\)。
如果是前者,那么显然 \(np\) 就是 \(q\) 的前驱,即 \(\operatorname{endpos}(q)\subseteq\operatorname{endpos}(np)\),直接赋值即可。
否则比较麻烦,即 \(np\) 表示的某个串是 \(q\) 的前驱。
else
{
int nq=++cnt;
memcpy(ch[nq],ch[np],sizeof(ch[nq]));
fa[nq]=fa[np];
fa[np]=fa[q]=nq;
len[nq]=len[p]+1;
for(;p && ch[p][c]==np;p=fa[p]) ch[p][c]=nq;
}
对于这种情况,我们需要分裂出一个点 \(nq\),令这个点 \(s_{nq}=s_p+c\) 。
可以发现由于 \(nq\) 是 \(np\) 的一个子集,\(np\) 的所有转移边 \(nq\) 也都有。
那么 fa[nq]=fa[np] 和 fa[np]=fa[q]=nq 也就很显然了。
接下来,\(nq\) 代替了 \(np\) 成为了 \(len\) 更短的点,那么显然所有连向了 \(np\) 的边都连向了 \(nq\)。
这样我们就建完了一棵SAM。
显然这样空间复杂度 \(O(n)\),因为我们插入一个字符最多会增加2个点。关于时间复杂度的证明详见OI WIKI。
接下来我们看一些经典套路:
1.求本质不同子串个数
首先对字符串 \(S\) 构造后缀自动机。
每个 \(S\) 的子串都相当于自动机中从根开始的路径。因此不同子串的个数等于自动机中以1为起点的不同路径的条数。
考虑到SAM是一个DAG,不同路径的条数可以通过动态规划计算。当然最后还要去掉空串。
时间复杂度 \(O(|S|)\) 。
当然这种方法有很大局限性,因为每一次都需要dfs一遍。所以大多数时候采用的都是下述方法:
我们知道一个字符串唯一对应一个节点,而一个节点表示的是长度为 \(len_u\) 的前缀中长度在 \((len_{fa},len_u]\) 的后缀。
所以显然有 \(\text{答案}=\sum{(len_{fa_u}-len_u)}\)。
2.字典序第 \(k\) 大子串
可以发现一个SAM是一个DAG,所以我们可以dp求出从一个点出发的子串数量。
那么很明显,我们从 'a'->'z' 依次查看,找到第一个满足子串数量前缀和 \(\geq k\) 的转移边,转移即可。
时间复杂度 \(O(|S|)\)。
3.动态求出现次数
给定文本串 \(S\) 和若干询问串 \(T_i\),动态询问 \(T_i\) 在 \(S\) 中出现次数。
我们知道,SAM本质上是将一个trie压缩后得到的结果,所以我们可以直接跳转移边得到。
最后得到的结果的状态数就是答案。状态数可以dfs预处理出来。
时间复杂度 \(O(|S|+|T|)\)。
4. 求两个前缀的LCS
这本来是归SA管的一道板子题,但偏偏有些出题人想要动态加字符。
可以发现,parent树本质是一棵压缩的trie树,保留其中的关键节点。
如果这是trie树,显然我们可以直接找trie上的LCA。而parent树保留的就是一棵虚树,所以显然也符合条件。
\(\color{black}{\text{O}}\color{red}{\text{IerWanHong}}\) \(\texttt{orz}\)。









 浙公网安备 33010602011771号
浙公网安备 33010602011771号