博弈论笔记--04--足球比赛与商业合作之最佳对策

Game One--点球
点球案例
在一次足球比赛罚点球时，罚球队员可以选择L,M,R三种不同射门路径；门将可以选择扑向左路或者右路（原则上讲他也可以守在右路）。

direction	L	R
L	4,-4	9,-9
M	6,-6	6,-6
R	9,-9	4,-4

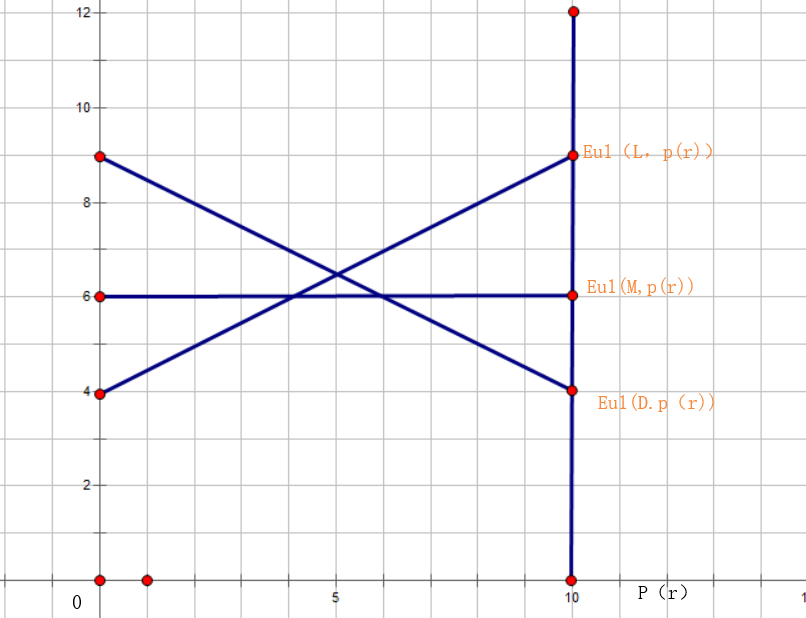Lesson:绝不选择在任何情况下都不是最佳反应的策略 当然这个缺少很多限制，所以结论并不准确。比如点球射门时，排除丢失的情况下，力度上升精度就会有所下降

最佳反应（经常缩写为\(BR\)）：
Player(i)选的的\(si^*\)策略就是对于其他博弈者选择\(S-i\)策略的最佳反应，其条件是\(U_i\)(\(Si^*\))--博弈者i选择策略i而非\(S-i\)获得的收益比选择其他策略(即\(Si'\))更高时，此处所有的\(Si'\)策略都适用于博弈者\(i\)
或者定义为：\(Si^*\)（Player(i)的策略）等于max \(U_i\)(s-\(s_i\)),即别人选择\(S-i\)时的最大收益
博弈者i的策略，对于其他博弈者的选择，所持有的信念P的最佳反应，条件是博弈者i在坚持信念\(P\)的情况下选择的期望收益大于选择其他策略---\(E\)(\(u_i\))(\(si^*\),\(P\)）\(>=E\)(\(u_i\))(\(S-i\),\(p\)）
期望收益=各项收益乘以对应概率 \(E=\)\(X_i\)*\(P_i\)（i~n）

合作关系博弈：两个人要为一个合办项目进行投资，届时将利润进行均摊。
转换为:
1. 两个代理人(博弈者)投资一个公司，没人分的50%利润，
同时每个代理人将根据自己的能力(努力程度)对公司进行投资
（S[0,4]代表贡献值，可以选择0~4这个闭区间之间任意的一个实数）
2. 利润公式为=4(\(s_1\)+\(s_2\)+b\(s_1\)\(s_2\)),其中b为一个相关参数，假设b=[0,1/4],并且一已知。
3. 从公式2可以看出多人合作会有协同作用，收益加成
4. \(U_1\)（\(S_1\),\(S_2\)）=\(1/2\)(\(4\)(\(s_1\)+\(s_2\)+\(b\)\(s_1\)\(s_2\)))\(-\)\(s_1^2\),
其中S1^2是投资成本，即为投入部分
\(U_2\)（\(S_1\),\(S_2\)）=\(1/2\)(\(4\)(\(s_1\)+\(s_2\)+\(b\)\(s_1\)*\(s_2\)))\(-\)\(s_2^2\),
其中S1^2是投资成本，即为投入部分

对于Player2每种可能的选择\(S_2\)，如何找到Player1会做的和后最佳反应？
由于此时的策略有无穷个，所以需要微积分。
1.求\(u_1\)的最大值，对u1求导，且ui=0,此时s1为自变量
即\(U_1\)=2(\(s_1\)+\(s_2\)+\(b\)\(s_1\)\(s_2\))\(-\)\(s_1^2\)=2\((1+\)\(b\)\(s_2\)\()-\)\(2\)\(s_1\)=0
即一阶导数为0，解的\(s_1=1+b*s_2\);
求二阶导数=-2<0，则可知所求为最大值.

则对s2的最佳反应为\(BR(s_1)=1+b*s_2\);
同理可得博弈者2对\(s_1\)的最佳反应为\(BR(s_2)=1+b*s_1\);

根据上述方程做出曲线可以得到博弈者1和博弈者2的最佳反应策略都在1~2之间，接着而删除了非最佳反应策略，重复画图（舍弃不是最佳反应的策略），最后最佳反应就会收敛于一个交集，即两者的交点,这个点叫做纳什均衡(Nash Equilibrium),简称NE,在这个点上，双方都采取最BR。

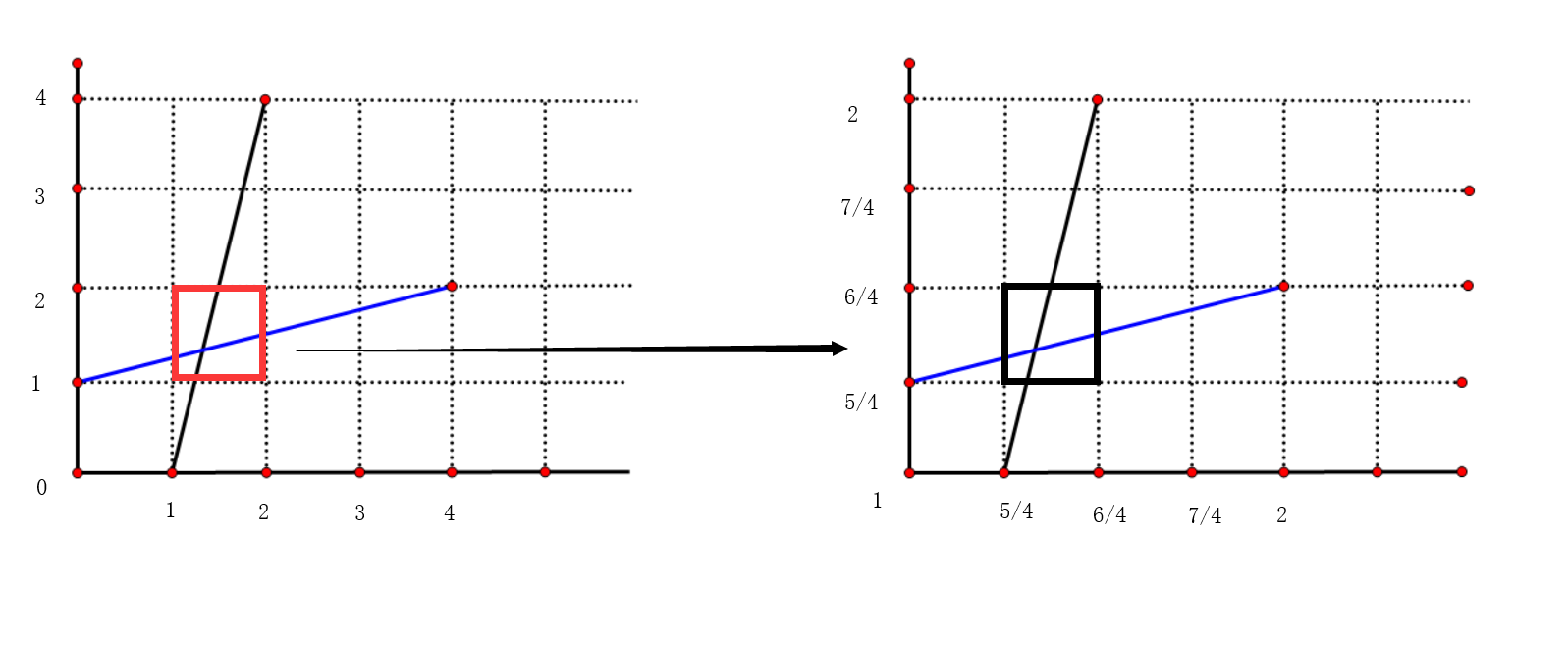
同时满足\(BR(S_1)\)和\(BR(S_2)\),得到\(s_1=s_2= 1/(1-b)\)，
结论：工作量减少了，效率反而降低了
理由：对自己的额外投资，需要承担所有的边际成本，但是却只能得到一半的利益，经济学上叫做"外部性"