LSMTree -> SStable 初体验

最近一直在听同事们说到SST结构，于是学习一波

一、文档介绍

本文写于2019-03-03 14:26:31，初学者个人见解，如有错误欢迎指正

基于LSM Tree的数据库有很多，Hbase，RockDB，LevelDB，本人以其中一种为例，简单介绍

二、 SST数据结构简介

SST全称“Sorted String Stable”，根据这个名称，我们初步可以知道这个数据结构内部的数据是排好序的（sorted），要想解释这个术语真正的含义，最好的办法是从他的出处找答案，我们翻开Google BigTable的论文，在这篇论文中是这样描述的：

The Google SSTable file format is used internally（内部的） to store（存储） Bigtable data. An SSTable provides a persistent（持久化的）, ordered immutable（不可改变的） map from keys to values, where both keys and values are arbitrary（任意的） byte strings. Operations are provided to look up the value associated（相关的） with a specified key, and to iterate（寻找） over all key/value pairs in a specified key range. Internally, each SSTable contains a sequence of blocks (typically each block is 64KB in size, but this is configurable). A block index (stored at the end of the SSTable) is used to locate blocks; the index is loaded into memory when the SSTable is opened.

Google SST文件格式被用于BIgTable内部数据，SStable是一种不可变的、排序的、持久化的key_value Map，其中key和value都是任意字节的字符串。提供了找寻特定Key值对应的value的操作，以及找寻给定范围内所有key_value的操作。每一个SStale包括一系列的block(一般block大小是64Kb，这个值是可以配置的)，在SST的末尾还有一个“block index”，用于定位每一个block(相当于索引)，是key_offset(偏移量)的索引。

前面的每一个data就是一个block，后面还有一个data index，其余的部分先不做解释，后文会详解SST内部结构，每一个block内部就是一系列的Key_value，前面的magic先忽略

这个排序好的SSTable结构和普通的key_value pair的区别在于，可以support: 1. range query 2. random w/r，但是就仅仅SStable本身无法高效的support以上需求，还需要一整套的机制来辅助完成从memory sort、flush to disk、compaction到快速读取的工作，这一个完整的机制和架构称为“The Log-Structed Merge-Tree” LSM Tree。

三、LSM Tree存储引擎

LSM Tree的全称是Log Structed Merge Tree，名字很形象，首先是基于Log的，不断产生SSTree结构的Log文件，并且是不断Merge以提高效率的，你看任何一篇介绍LSM Tree的文章都很难将它与树联系起来，事实上，它是一种分层的组织数据的结构，具体到实现上就是一些按照逻辑分层的有序文件（下文介绍）

LSM Tree的节点可以分为两类，在内存中的称之为MemTable，保存在磁盘上的称为SSTable，这里再提醒大家一点，请记得前面介绍SSTable的时候说的，SSTable是不可更改的。

仔细来讲，MemTable与SSTable还是又很多区别的，这里就提醒一下，不展开讨论

我们希望LSM Tree可以提供快速的读与快速的随机写，下面介绍一下哪些机制保证了效率：

磁盘内SSTable的index始终位于内存中，这一条为快速读提供了支持
所有的写都是直接写在内存中的MemTable中的，这一条为快速随机写提供了支持
读操作的顺序是，首先在MemTable内寻找，找不到的话再在SSTable内检索
MemTable会定期将自身内容写到disk内的
disk内的SSTable会定期合并（原文是“collapsed together”）

在内存中写操作是经常发生的，写操作是直接写入MemTable，当MemTable达到一定的size，就flush到disk内成为一个不可变(immutable)的SSTable。与此同时，我们会保持(maintain)所有SSTable的index在内存中，这样在对给定的key进行搜索的时候，我们首先在MemTable内进行检索，再在每一层的SSTale之间再进行搜索，到这里就介绍了LSMTree存储引擎是如何提高读写效率的了，那对于更新与删除操作呢？

对于更新操作，因为SSTable是不可变的，因此更新与删除操作只发生在内存的MemTable内，如果要对SSTable内的数据进行更新只需要重新写进去一个新的就可以了，因为对于SSTable的访问是顺序的，所以新内容的存在会覆盖旧内容，也就是顺序访问到需要的值的时候就会退出，以下的旧值不被访问到。对于删除操作，也是在MemTable内插入一个墓碑标志加值，代表这个值被删除了，然后访问的时候会提前访问到墓碑标志而得知该值已经被删除了

下面来说一下LSM Tree的树形结构，对于几百上千个SSTable，我们要定期进行操作，SSTale是分等级的，如图所示

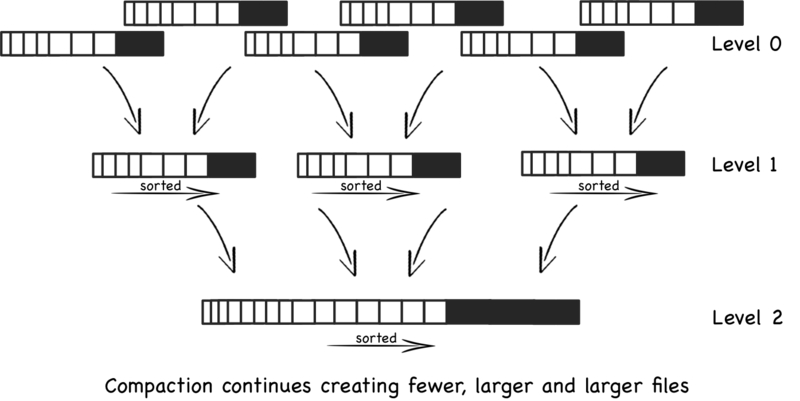
每层SSTable的文件到达一定条件之后进行合并操作，然后放置到更高层，合并操作在实现上都是策略驱动的、可插件化的。MemTable flush to disk的时候是直接到Level 0层的，每一层有很多SSTable，Level 0层的SSTable 是不同的MemTable flush进来的，每个SSTable内部是排好序的，但是SSTable之间不一定是排好序的，可能两个SSTable之间会出现重叠的部分，这由写入操作的随意性决定，在Level 1以及以后的层次中的SSTable，都是由上一层合并得到的，所以内部是排好序的，外部也是排好序的，之间key range之间不会存在交集。SSTable之间的合并类似于简单的归并排序，根据key值确定要合并(merge)的文件，然后进行合并。因此，合并一个文件到更高层可能需要写多个文件，存在一定程度上的写放大。不同的数据库会采用不同的办法来优化或者限制恶劣的情况发生。

接下来我们引入一下Bloom Filter(布隆过滤器)，我们之前在读操作中已经说了，首先判断是否在MemTable中，然后根据index将覆盖该key range的不同层的所有SSTale都查找一遍，简单但是低效，优化的方式又两种，第一种就是前面介绍的在每一个SSTable尾部加入key_offset index索引，第二种就是在每一个SSTable内加布隆过滤器。

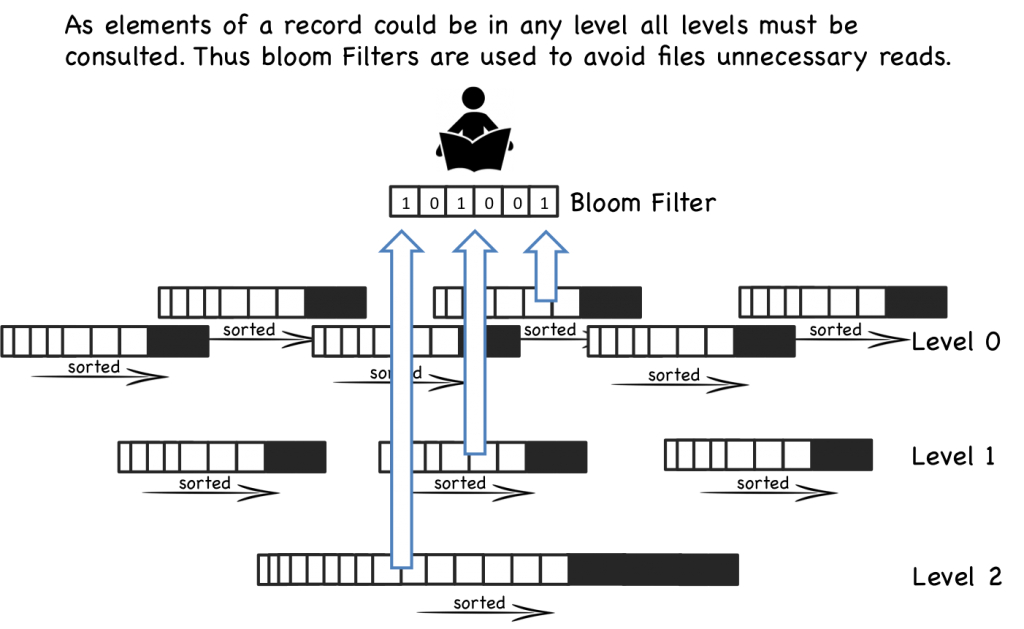
四、Bloom Filter（布隆过滤器）

我们在设计一个算法的时候一般都会考虑时间效率与空间效率之间的平衡，Bloom Filter是一种占用很少空间，并且提供常数级查询的数据结构，但是他也有一些无法忽略的缺点，就是会有一定的误判率（false positive rate）。Bloom Filter经常用在大数据处理中，最常用来检索元素是不是子啊集合内，在我们上面的例子上就是判断key range是否在SSTable内，下面介绍具体是如何实现的。

我们都了解过哈希函数，不存在一种哈希函数能够完全区别出来所有值，也就是说无论采用怎样的哈希函数，都可能使得两个值哈希成同一个值，但是两个值，采用k种哈希函数都能哈希到同一个值上的概率非常小，Bloom Filter就是利用了这一点性质。一个Bloom Filter的物理结构其实是一个bit vector。这个bit vector的每一位初始的时候都被设为0。同时, 每个Bloom Filter 都伴随着k个hash functions。往Bloom Filter插入元素的过程就是用每个hash function计算这个元素, 从而将结果所对应的比特位改为1。如果当前比特位已经为1, 则在插入的过程保持这一位不变。当判断一个值是否存在的时候就是用k个hash function来哈希这个值，来和bit vector的结果位进行比较，只要有一位为空，就可以代表这个值不存在，反之，如果都不是空，也不能代表这个值就是存在的，详情见下图，因为可能别的数字将对应的结果位置成了1

在这个示例中, 我们的Bloom Filter由一个30 bits的Bit Vector以及3个Hash Functions来构成。我们将三个元素 $S_{1}$

五、参考链接：

$S_{1}$

https://www.cnblogs.com/fxjwind/archive/2012/08/14/2638371.html

http://www.blogjava.net/dlevin/archive/2015/09/25/427481.html

六、存疑

LSMTree在BigTable中是如何作用的

posted @ 2019-03-03 17:09 Flower_Z 阅读(883) 评论(0) 编辑收藏举报

刷新页面返回顶部

LSMTree -> SStable 初体验

公告