【浮*光】 #noip模拟# 2018.08.29
T1 seq
【问题描述】
给一个长度为 𝑁 的序列 𝐴 ,你可以把 𝐴 中的 0 改成其他的数字.
(正数,负数, 0均可,不同的 0 可以改成不同的而数字),
要求修改后 𝐴 最长上升子序列的长度最大.输出这个长度.
【输入格式】
第一行一个 𝑁 ,表示数字的个数.
接下来 𝑁 个数字,第 𝑖 个表示 𝐴𝑖.
【输出格式】
一个数字,答案.
【数据规模】
对于 20% 的数据, 𝑁 ≤ 20, 𝐴𝑖 ≥ 1 .
对于 60% 的数据, 𝑁 ≤ 1000 .
对于另 10% 的数据, 𝐴𝑖 ≤ 10 .
对于 100% 的数据, 𝑁 ≤ 10^5, 0 ≤ 𝐴𝑖 ≤ 10^9.
【题目解答】
题意为:给一个序列,你可以把序列中的 0 随意修改,要求最大化 LIS 的长度.
记 𝑆𝑖 表示前 𝑖 个数字中 0 的个数,可以写出一个很显然的 dp.
𝑑𝑝[𝑖]= max (𝑗<𝑖,𝑎𝑗<𝑎𝑖) { 𝑑𝑝[𝑗] + min{ 𝑎𝑖 − 𝑎𝑗 − 1, 𝑆𝑖 − 𝑆𝑗 } }。
时间复杂度 𝑂(𝑁^2) .使用数据结构可以做到 𝑂(𝑁 log2𝑁 ).
然后只需注意到一定存在一种最优解使得所有的 0 都被加了进来,
所以 0 的个数加上对所有非 0 数的 𝑎𝑖 − 𝑆𝑖 算 LIS 的长度就是答案.
时间复杂度 𝑂(𝑁 log 𝑁 ) .
#include <cmath> #include <iostream> #include <cstdio> #include <string> #include <cstring> #include <vector> #include <algorithm> #include <stack> #include <queue> #include <deque> using namespace std; typedef long long ll; typedef unsigned long long ull; /*【seq】 给一个长度为𝑁的序列𝐴,可以把0改成其他的数字。 -----> 正数,负数,0均可,不同的0可以改成不同的数字。 要求修改后𝐴最长上升子序列的长度最大。输出这个长度。 */ deque<int> dq; //双端队列:支持在两端高效地插入删除元素的连续线性存储空间 int main(){ int n,num0=0; cin >> n; dq.push_front(INT_MIN); //队头初始化为-inf for(int i = 0; i < n; i++) { int t; cin >> t; if(t == 0) { num0++; dq.push_front(INT_MIN); } else{ int cnt=lower_bound(dq.begin(),dq.end(),t-num0)-dq.begin()-1; int best=cnt+1; if(best==dq.size()) dq.push_back(INT_MAX); dq[best]=min(dq[best],t-num0); } } cout << dq.size()-1 << endl; return 0; }
T2 paint
【问题描述】
给出一张 𝑁 个点, 𝑀 条边的图 𝐺(𝑉, 𝐸 ) ,点的标号是 0 到 𝑁 − 1 .
对于每个非空点集 𝑆 (共有 2^𝑁−1 个),
定义 𝑓 (𝑆 ) = min{𝑘|𝑆存在𝑘 −染色方案},要求对每个 𝑆 都计算 𝑓 (𝑆 ) .
定义一个点集 𝑆 的 𝑘−染色方案是指对所有的 𝑢 ∈ 𝑆 确定一个 𝐿𝑢 ∈ [1, 𝑘 ] ,
使得所有 𝑢 ∈ 𝑆, 𝑣 ∈ 𝑆, (𝑢, 𝑣) ∈ 𝐸 的点对 (𝑢, 𝑣) 有 𝐿𝑢 != 𝐿𝑣.
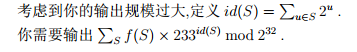
【输入格式】
第一行一个数 𝑁 ,表示点数.
接下来 𝑁 行,每行一个长度为 𝑁 的 01 串,表示邻接矩阵.
数据保证合法.
【输出格式】
一个数字,答案.
【数据规模】
对于 30% 的数据, 𝑁 ≤ 4 .
对于 60% 的数据, 𝑁 ≤ 10 .
对于 100% 的数据, 𝑁 ≤ 18 .
【题目解答】
给一张无向图,要求对于每个非空点集都计算色数.𝑁 ≤ 18.

T3 trie
【问题描述】
有 𝑁 个串,有 𝑄 个询问,每次询问用 𝑙, 𝑟 描述,
表示询问编号在 [𝑙, 𝑟] 中的串有多少个不同的前缀.
【输入格式】
第一行一个数字 𝑁 ,表示串的个数.
接下来 𝑁 行,每行一个串.
接下来一个 𝑄 ,表示询问次数.
接下来 𝑄 行,每行两个数 𝑙0, 𝑟0,表示询问区间,
为了强制在线,你需要做以下操作:
𝑙 = (𝑙0 + 𝑙𝑎𝑠𝑡𝑎𝑛𝑠) 𝑚𝑜𝑑 𝑛 + 1
𝑟 = (𝑟0 + 𝑙𝑎𝑠𝑡𝑎𝑛𝑠) 𝑚𝑜𝑑 𝑛 + 1
𝑖𝑓 ( 𝑙 > 𝑟 ) 𝑠𝑤𝑎𝑝( 𝑙 , 𝑟 )
𝑙𝑎𝑠𝑡𝑎𝑛𝑠 表示上一次询问的答案,初始为 0 .
【输出格式】
𝑄 行,每行一个数表示答案.
【数据规模】

【题目解答】
有 𝑁 个串,有 𝑄 次询问,每次把一个区间里的串插到 trie 里,问有多少个节点.
算法一
把所有的串拉进去建一个 trie ,每次询问就变成求关键点到根路径并的大小,
把关键点按照 dfs 排序后就变成深度和减排序后相邻两点 lca 的深度和.
考虑维护后者,把序列分块,处理出块到块之间后者的值,
这个可以用主席树解决,询问也类似.
时间复杂度 𝑂((𝑁 + 𝑄)√𝑁 log 𝑁 ) ,期望得分 70 分.
算法二
把序列的前缀 hash 以后排成一排,
问题就变成了区间 [𝑙, 𝑟] 中有多少个不同的数字.
用 𝑝𝑟𝑒 𝑖 表示 𝑖 前面一个和 𝐴𝑖 相同的位置,
问题就变成求 𝑝𝑟𝑒 𝑖 < 𝑙, 𝑙 ≤ 𝑖 ≤ 𝑟的 𝑖 的个数,
这是一个二维数点问题,直接主席树即可.
——时间划过风的轨迹,那个少年,还在等你。


