【暖*墟】 #洛谷提高网课# 8.1初级数据结构(1)
链表
当平时使用数组时,有时会遇到一些问题:
- 在删除一个数据时,为了保证数据的连续性,
- 需要将删除点右边的数据、全部往左移一格。
- 在插入一个数据时,为了保证数据的连续性,
- 需要将插入点右边的数据、全部往右移一格。
- 每次移动的时间复杂度为O(N),如果元素较多时会时间超限。
链表一个位置包括了自己位置上的值和下一个值所在的位置。
这样链表就可以实现O(1)的插入/删除,同时保证数据的连续性。
一般使用数组模拟。v[i]表示当前位置的数字,nex[i]指向下个位置的数组坐标。
- 在使用链表时可能需要知道上个位置在哪里,于是有了双向链表。
- 双向链表多使用一个pre[i]表示上个位置的数组坐标。
栈和队列
栈在一端的出口同时控制加入和踢出,另一端的出口为封闭的, 满足后进先出原则。
队列在尾控制加入,在头控制踢出,满足先进先出原则。
- 栈:用一个数组S代表栈,l为元素数量,加入元素x。
- S[++l]=x;弹出栈顶元素到x;x=S[l--];
- 队列:用一个数组Q代表队列,l为队列头,r为队列尾,加入元素x。
- Q[++r]=x;弹出队头元素到x;x=Q[l++]。
单调栈和单调队列
单调栈除了满足普通栈的性质外,还满足从栈顶到栈底的元素具有严格的单调性。
假设我们维护的是一个单调递减的栈: (找到合适的位置)
• 若进栈的元素为x,栈顶元素为S[l]。
• 那么当x>=S[l]时弹出栈顶元素,直到x<S[l]为止,压入元素x。
单调队列除了满足普通队列的性质外,还满足从队列头到队列尾的元素具有严格的单调性。
假设我们维护的是一个单调递减的队列:
• 若进队的元素为x,队尾元素为Q[r]。
• 那么当x>=Q[r]时弹出队尾元素,直到x<Q[r]为止,加入元素x。
例题1 - 洛谷P1886 滑动窗口 (单调队列)
例题2 - 洛谷P1725 琪露诺(单调队列优化dp)
- 格子编号为0到N,每次移动可以到[i+L,i+R]中的一格,
- 然后收集格子上的冰冻值A[i],最后一次移动时只要大于N 就算到达。
- 求经过的格子最大冰冻值和。
SOLUTION
代码实现

#include<iostream> #include<cstdio> #include<iomanip> #include<cstring> #include<cmath> using namespace std; int n,l,r,a[200005],f[400005]; int q[200005],head=1,tail=0; int main(){ cin>>n>>l>>r; for(int i=0;i<=n;++i) scanf("%d",&a[i]); for(int i=n+l;i>=l;--i){ //反向算,方便确定来源,dp填表法 while(f[q[tail]]<=f[i]&&head<=tail) tail--; //↑↑↑单调队列找插入位置,栈底的元素大 q[++tail]=i; //找到位置,把i加进单调队列 f[i-l]=max(f[i-l],f[q[head]]+a[i-l]); //区间最优选择进入dp比较 if(q[head]==i+r&&head<=tail) head++; } cout<<f[0]<<endl; return 0; }
例题3 - 洛谷P1419 寻找段落(前缀和+二分答案)
- 给定一个长度为n的序列a[i],定义a[i]为第i个元素的价值。
- 现在需要找出序列中最有价值的“段落”。段落的定义是长度在[S,T]之间的连续序列。
- 最有价值段落是指平均值最大的段落,段落的平均值=段落总价值/段落长度。
SOLUTION


#include<cstdio> #include<cstring> #include<iostream> using namespace std; const int maxn = 100000+10; int A[maxn],n,s,t; double sum[maxn]; int q[maxn],front,rear; bool can(double x) { sum[0]=0; for(int i=1;i<=n;i++) //处理前缀和 sum[i] = sum[i-1]+A[i]-x; front=1; rear=0; //初始化单调队列 for (int i = 1; i <= n; i++) { if (i >= s) { //足够s个 while (rear >= front && sum[i - s] < sum[q[rear]]) rear--; //↑↑↑ front为在i-t..i-s区间内的最小值 q[++rear] = i - s; //入队区间起点-1 } if (front <= rear && q[front] < i - t) front++; //维护区间i-t if (front <= rear && sum[i] - sum[q[front]] >= 0) return true; //有大于0的区间和说明最大平均值还可以更大 } return false; } int main() { scanf("%d%d%d",&n,&s,&t); double L=0,R=0; for(int i=1;i<=n;i++) { scanf("%d",&A[i]); R=max(R,(double)A[i]); //预处理找出max } while(R-L>1e-4) { //二分答案 double M=L+(R-L)/2; if(can(M)) L=M; else R=M; } printf("%.3lf\n",L); return 0; }
例题4 - 洛谷P1823 音乐会的等待(单调栈维护)
- N个人正在排队进入一个音乐会。人们想在队伍里寻找自己的熟人。
- 队列中任意两个人A和B,如果他们相邻或他们之间没有人比A或B高,
- 那么他们是可以互相看得见的。写一个程序计算出有多少对人可以互相看见。
SOLUTION



#include <iostream> #include <cstdio> #include <algorithm> #include <cmath> #include <cstring> #include <vector> #define ll long long using namespace std; ll n,ans; ll z[500010],now,tmp,i; inline int read(){ //快读 int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int main(){ scanf("%lld",&n); tmp=read(); z[1]=tmp; now=1; for(i=1;i<n;i++){ tmp=read(); if(tmp<z[now]) { ans++; z[++now]=tmp; } else{ int l=1,r=now,m; while(l<r){ m=(l+r)>>1; //取mid if(r==l+1) m=r; if(z[m]>tmp) l=m; else r=m-1; } ans+=now-l+1; //增加的人数 while(now>0&&z[now]<tmp) now--; z[++now]=tmp; } } printf("%lld",ans); return 0; }
并查集
并查集用于一类判断和修改连通性的问题。
比如给𝑛个点,𝑚条边,有两种操作,问𝑥𝑖和𝑦𝑖是否联通 + 联通𝑥𝑖和𝑦𝑖。
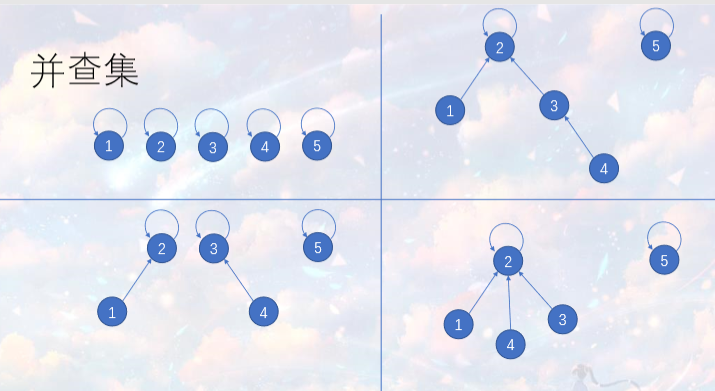
路径压缩
这种写法由于可能进行层数较多的合并,均摊到达O(M log N)。
int find(int x) { return fa[x]==x? x:fa[x]=find(fa[x]); } int find(int x) { if (fa[x]==x) return x; else return fa[x]=find(fa[x]); }
按秩合并
按秩合并的基本思想是使包含较少结点的树的根指向包含较多结点的树的根,
而这个树的大小可以抽象为树的高度,即高度小的树合并到高度大的树,
这样使加上按秩合并后并查集的复杂度可以减少到O(M Alpha(N))。
void unite(int x,int y){ x=find(x); y=find(y); if(x==y) return; if(rank[x]<rank[y]) fa[x]=y; // 合并:从rank小的向rank大的连边 else{ fa[y]=x; if(rank[x]==rank[y]) rank[x]++; } }
例题1 - 洛谷P1195 口袋的天空
给你云朵的个数 N ,再给你 M 个关系,表示哪些云朵可以连在一起和连接的代价。
现在小杉要把所有云朵连成 K 个棉花糖,一个棉花糖最少要用掉一朵云,
怎么连花费的代价最小?无解输出'No Answer'。𝑁 ≤ 1000, 𝑀 ≤ 10000, 𝐾 ≤ 10 。
SOLUTION


#include<iostream> #include<cstdio> #include<algorithm> using namespace std; const int size = 200010; struct node{ int f,t,d; //front,tail,d是价值 }l[size]; int f[size]; int find(int x){ if(f[x] == x) return x; return f[x] = find(f[x]); } bool cmp(node a,node b){ return a.d < b.d; //按权值排序 } int main(){ int n,m,k; scanf("%d%d%d",&n,&m,&k); k = n-k; int ans = 0; //总共要取 N - K条边 for(int i = 1 ; i <= m ; i ++) scanf("%d%d%d",&l[i].f,&l[i].t,&l[i].d); sort(l+1,l+m+1,cmp); for(int i = 1 ; i <= n ; f[i] = i , i ++); for(int i = 1 ; i <= m ; i ++){ int x = find(l[i].f); int y = find(l[i].t); if(x != y){ k --; f[x] = y; ans += l[i].d; } if(k == 0) break; } if(k) puts("No Answer"); //边没有取完,返回无解 else cout<<ans; return 0; }
例题2 - 洛谷P1196 银河英雄传说
例题3 - 洛谷P1525 关押罪犯
一共有N个罪犯,之间关系表示为:𝑥𝑖和𝑦𝑖如果在同一个监狱中,会有𝑐𝑖的冲突。
你现在需要将这些罪犯分到两个监狱中,使得造成冲突事件的最大值最小。
SOLUTION



#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<string> #include<queue> #include<vector> #include<cmath> #include<map> using namespace std; /*【关押罪犯】 S 城现有[两座监狱],一共关押着N 名罪犯,编号分别为1~N。 很多罪犯之间积怨已久,如果客观条件具备则随时可能爆发冲突。 我们用“怨气值”(一个正整数值)来表示某两名罪犯之间的仇恨程度。 如果两名怨气值为c的罪犯在同一监狱,会造成影响力为c的冲突事件。 每年年末,警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表, 市长只会去看列表中的第一个事件的影响力,如果影响很坏,他就会考虑撤换警察局长。 如何分配罪犯,才能使Z 市长看到的那个冲突事件的影响力最小?这个最小值是多少? */ struct node{ int x,y,z; }q[100009]; bool cmp(node a,node b){ return a.z>b.z; } int fa[100009],no[100009]; int findfather(int x){ if(fa[x]==x) return x; fa[x]=findfather(fa[x]); return fa[x]; } int adds(int x,int y){ int fx=findfather(fa[x]); int fy=findfather(fa[y]); fa[fx]=fy;//祖先合并 } int checks(int x,int y){ //查询关系 int fx=findfather(x); int fy=findfather(y); if(fx==fy) return true; return false; } int main(){ int n,m; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) fa[i]=i; for(int i=1;i<=m;i++) scanf("%d%d%d",&q[i].x,&q[i].y,&q[i].z); sort(q+1,q+m+1,cmp); //按z值从大到小排序 for(int i=1;i<=m+1;i++){ if(checks(q[i].x,q[i].y)) { printf("%d",q[i].z); break; } //如果两个罪犯已经在同一监狱就输出 ,并退出 else{ if(!no[q[i].x]) no[q[i].x]=q[i].y; //没标记最大敌人,就标记 else adds(no[q[i].x],q[i].y); //将敌人的敌人合并 if(!no[q[i].y]) no[q[i].y]=q[i].x; else adds(no[q[i].y],q[i].x); } } return 0; }
堆
堆用于一类支持插入的快速维护序列的最大/最小值的问题。
其根本是利用二叉树作为基础,在二叉树的节点上维护堆的特性。
• 大根堆的特性为𝑣父亲 ≥ 𝑣左儿子,且𝑣父亲 ≥ 𝑣右儿子。
• 小根堆的特性为𝑣父亲 ≤ 𝑣左儿子,且𝑣父亲 ≤ 𝑣右儿子。
堆的插入
• 如果你标号时从1开始,那么堆中父亲和儿子的寻找将非常方便。
• 对于一个点n,其父亲为n/2,左儿子为n*2,右儿子为n*2+1。(完全二叉树)
• 具体实现插入时,我们只需要从插入的点自下而上不停维护大根堆的性质,
• 即有父亲小于其儿子即交换父亲和儿子的位置,接着把要校验的点转移为当前点的父亲即可。
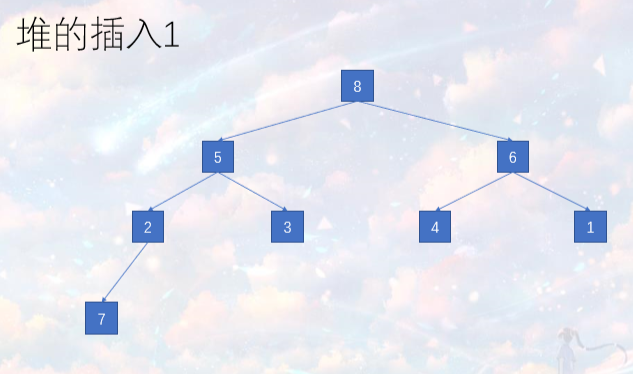
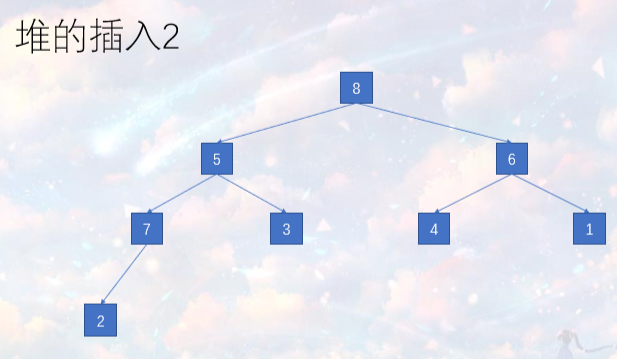
堆的删除
具体实现:删除堆顶时,我们先将堆顶和末尾交换,然后堆大小-1,
接着从堆顶自上而下地维护堆的性质,即有父亲小于其儿子,
交换父亲和儿子的位置,接着将要校验的点转移为交换过的儿子。
堆的stl函数

例题:
洛谷P1090 合并果子
洛谷P1801 黑匣子
CF-639D Bear_and_Contribution
trie例题:
洛谷P2580 于是他错误的点名开始了
CF-706D Vasiliy's Multiset
CF-456D A Lot of Games
课后练习:
• 洛谷P1160 队列安排
• 洛谷P1449 后缀表达式
• 洛谷P1901 发射站
• 洛谷P2024 食物链
• CF-725D Contest Balloons
• CF-665E Beautiful Subarrays
——时间划过风的轨迹,那个少年,还在等你。









