【暖*墟】 #二叉堆# 大根堆的常见操作

一、二叉堆的定义

二叉堆使用完全二叉树（其前n-1层必须被填满，第n层也要从左到右顺序填满）来实现。

在二叉堆中，所有非终端结点的值均不大于（或不小于）其左右孩子的值。

若非终端结点的值均不大于其左右孩子结点的值，这样的二叉堆叫做小根堆（下图b），

小根堆根结点的值是该堆中所有结点的最小值；

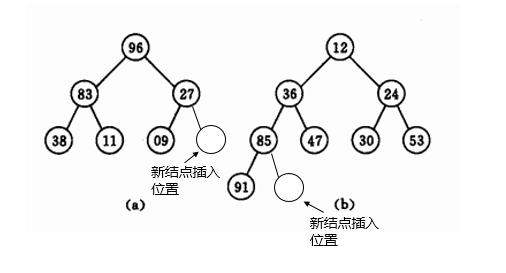
同样的，若非终端结点的值都不小于其左右孩子的值，这样的堆叫做大根堆（下图a），

大根堆根结点的值为改堆所有结点的最大值。利用堆的此性质，可以实现堆排序。

说明：小根堆和大根堆的实现没有太大的区别，所以下面以大根堆为例。

二、二叉堆的操作

堆一般使用数组来构建，假设为数组a[]，结点通常存储在a[1]，

这样对于下标为k的结点a[k]来说，其左孩子的下标为2*k，右孩子的下标为2*k+1。

1、插入结点到堆中

结点插入的位置应该是完全二叉树的最后一个位置（如下图所示），

对于大根堆来讲，需要满足两个性质：

（1）堆为完全二叉树；（2）堆中每个父结点的值都不小于其左右子结点的值。

插入结点可能会破坏这两条性质，所以在插入结点后需要对堆进行调整。

调整方法为：将插入的结点与其父结点比较，若大于其父结点的值，则交换两者。

重复此操作，直至该结点不比其父结点大，或者该结点成为根结点。

可以通过插入结点到一个已经存在的堆中，也可以通过不断插入结点来构建一个堆。

 

//insert
int heap[maxn],n;
void up(int p){ //通过交换位置p实现向上调整
    while(p>1){ //没有到达根节点
        if(heap[p]>heap[p/2]){
            swap(heap[p],heap[p/2]);
            p/=2; //编号变小：(2n+1)/2=2n/2=n。
        }
        else break; //找到位置，退出循环
    }
}
void insert(int val){
    heap[++n]=val; up(n); //放在底端，记录价值
}

↓↓↓GetTop：返回堆顶权值

//gettop
int gettop(){
    return heap[1];
}

2、删除堆顶元素（堆排序）

删除堆顶元素（根结点）后，会得到左右两棵子树，此时将堆中最后一个元素移到堆顶，

然后自上而下调整，将该结点与左右孩子结点比较，此时会有三种情况：

（1）结点的左右孩子均为空，此时调整结束；

（2）结点只有左孩子，将该结点与左比较。若结点小于其左孩子，则两者交换，否则调整结束；

（3）结点左右孩子都非空，则将该结点与左右较小者比较，若小于则交换，否则调整结束；

重复此过程，直到该结点不小于其左右孩子结点，或者该结点为叶子结点。

//extract
//删除堆顶元素，将末尾元素放到堆顶位置，再调整
void down(int p){ //向下调整
    int s=p*2; //p的左子节点
    while(s<=n){ //还没成为叶子结点
        if(s<n&&heap[s]<heap[s+1]) s++; //取左右节点较大值
        if(heap[s]>heap[p]){
            swap(heap[s],heap[p]);
            p=s,s=p*2; //现在位置变成s，子节点s相应改变
        }
        else break;
    }
}
void extract(){
    heap[1]=heap[n--]; //n处元素放在堆顶，n--
    down(1);
}

3、删除p处元素

//remove(p)
 
void up(int p){ //通过交换位置,实现向上调整
    while(p>1){ //没有到达根节点
        if(heap[p]>heap[p/2]){
            swap(heap[p],heap[p/2]);
            p/=2; //编号变小：(2n+1)/2=2n/2=n。
        }
        else break; //找到位置，退出循环
    }
}
 
void down(int p){ //向下调整
    int s=p*2; //p的左子节点
    while(s<=n){ //还没到末尾
        if(s<n&&heap[s]<heap[s+1]) s++; //取左右节点较大值
        if(heap[s]>heap[p]){
            swap(heap[s],heap[p]);
            p=s,s=p*2; //现在位置变成s，子节点s相应改变
        }
        else break;
    }
}
 
void remove(int p){
    heap[p]=heap[n--]; //n处元素放在k处，n--
    up(p); down(p); //可能向上或者向下调整
}

三.stl中的优先队列

priority_queue实现了一个大根堆。

支持 push（i），top（），pop（）操作，不支持 remove 操作。

priority_queue<int> xxx 大根堆

priority_queue<int, vector<int>, greater<int>> xxxx 小根堆

//注意，多重符号时中间要打空格分隔符，否则‘>>’会影响。

 

                                                   ——时间划过风的轨迹，那个少年，还在等你。