【暖*墟】#数论# 欧拉函数的学习与练习
欧拉函数的定义
ϕ(n):对于整数n,小于等于n、且与n互质的正整数的个数。
欧拉函数的计算方法
√n计算单值欧拉函数:计算ϕ(n),分情况讨论。
1.当n=1时,很明显,答案为1。
2.当n为质数时,根据素数的定义,答案为n−1。
3.当n为合数时,对n进行质因数分解:设n=a1^p1∗a2^p2...∗ak^pk,
(1)假设k=1,即n=a1^p1、只有一个因数就是素数a1。
- 那么:ϕ(p^k)=p^k−p^(k−1)。
- 证明:容斥原理知,答案=n-与它不互素的数的个数,
- p是素数,在p^k中与其不互素的数为1∗p,2∗p....p^(k−1)∗p,共p^(k−1)个。
(2)当k≠1时,ϕ(n)=ϕ(a1^p1∗a2^p2...∗ak^pk)。
- 通过k=1求得的性质可知:
ϕ(n) = ∏(i=1~k)ai^Pi−ai^(Pi−1)
= ∏(i=1~k)(ai^Pi)*(1-1/ai)
= n∗∏(i=1~k)(1-1/ai)
= n∗∏(i=1~k)((ai-1)/ai);
int euler(int x){ int ans=x; for(int i=2;i*i<=x;i++) if(x%i==0){ ans=ans/i*(i-1); while(x%i==0) x/=i; } if(x>1) ans=ans/x*(x-1); return ans; //返回ϕ(x)的值 }
欧拉函数的性质
1.ϕ(n)为积性函数。即:gcd(a,b)=1时,ϕ(ab)=ϕ(a)*ϕ(b)。
积性函数:若一个定义在正整数域上的函数f(x),
对于任意满足gcd(x,y)==1的x、y都有f(xy)=f(x)∗f(y)。
常见积性函数:莫比乌斯函数μ(n),欧拉函数ϕ(n),
一个数n的约数个数d(n),一个数n的约数和σ(n),f(x)=x^k(k∈N)......
证明欧拉函数是积性函数:
狄利克雷卷积:若 f(x),g(x) 都是积性函数,则狄利克雷卷积 h(x)=∑(d|x)f(d)*g(x/d) 。
- 性质:若f(x),g(x)都是积性函数,则狄利克雷卷积也是积性函数。
积性函数的性质:任意积性函数都可以线性筛(在严格O(n)时间复杂度内筛出)。
2.∑(d|n)ϕ(d)=n。
3.1到n中与n互质的数的和为n∗ϕ(n)/2 (n>1)。
- 证明:若gcd(n,i)=1,那么gcd(n,n−i)=1。
- 即,与n互质的数都是成对出现的。且每一对的和都为n。
4. a^(ϕ(n))≡1(modn)。

欧拉函数的线性筛法
利用三个性质:
性质1 若p为素数,则φ(p)=p−1。
性质2 若i mod p≠0 ,且p为素数,则φ(i∗p)=φ(i)∗φ(p)=φ(i∗p)=φ(i)∗(p−1)。
性质3 若i mod p=0 ,且p为素数,则φ(i∗p)=φ(i)∗p。详情见 这里
int phi[MAXN],vis[MAXN],prime[MAXN],tot=0; void GetPhi(int n){ phi[1]=1; //特例:ϕ(1)=1; for(int i=2;i<=n;i++){ if(!vis[i]) prime[++tot]=i,phi[i]=i-1; //i是素数(1) for(int j=1;j<=tot&&i*prime[j]<=n;j++){ //枚举“i*质数” vis[i*prime[j]]=1; //标记“i*质数”为合数 if(i%prime[j]==0) //(3)注意这里可以直接break; {phi[i*prime[j]]=phi[i]*prime[j];break;} else phi[i*prime[j]]=phi[i]*(prime[j]-1); }//(2) } for(int i=1;i<=n;i++) cout<<phi[i]<<endl; }
欧拉函数与原根
概念引入:由费马小定理可知,如果a于p互质,则有a^(p-1)≡1(mod p)。
对于任意的a是不是一定要到p-1次幂才会出现上述情况呢?显然不是。
p确定,对于某个a值,当第一次出现a^k≡1(mod p)时, 记为ep(a)=k。
如果k=p-1,称a是p的原根。--> 每个素数恰好有φ(p-1)个原根(φ(x)为欧拉函数)。
- 定理:原根个数为φ(φ(m));对于质数m,由于φ(m)=m-1,所以为φ(m-1)。

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<queue> #include<string> #include<cmath> #include<map> using namespace std; typedef long long ll; // poj1284 Primitive Roots //原根与欧拉函数 // 【题意】 求奇素数的原根的个数。 // 原根个数为φ(φ(m));对于奇素数m,由于φ(m)=m-1,所以为φ(m-1)。 int euler(int x){ int ans=x; for(int i=2;i*i<=x;i++) if(x%i==0){ ans=ans/i*(i-1); while(x%i==0) x/=i; } if(x>1) ans=ans/x*(x-1); return ans; //返回ϕ(x)的值 } int main(){ int x; while(scanf("%d",&x)!=EOF) cout<<euler(x-1)<<endl; }

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<queue> #include<string> #include<cmath> #include<map> using namespace std; typedef long long ll; // CF284A Cows and Primitive //原根与欧拉函数 // 【题意】 求素数的原根的个数。 // 原根个数为φ(φ(m));对于素数m,由于φ(m)=m-1,所以为φ(m-1)。 int euler(int x){ int ans=x; for(int i=2;i*i<=x;i++) if(x%i==0){ ans=ans/i*(i-1); while(x%i==0) x/=i; } if(x>1) ans=ans/x*(x-1); return ans; //返回ϕ(x)的值 } int main(){ int x; scanf("%d",&x); cout<<euler(x-1)<<endl; }
欧拉函数的相关习题

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<queue> #include<string> #include<cmath> #include<map> using namespace std; typedef long long ll; // UVA10299 Relatives // 多组数据,每组计算给定数的欧拉函数。 int euler(int x){ int ans=x; for(int i=2;i*i<=x;i++) if(x%i==0){ ans=ans/i*(i-1); while(x%i==0) x/=i; } if(x>1) ans=ans/x*(x-1); return ans; //返回ϕ(x)的值 } int main(){ int x; while(scanf("%d",&x)&&x) { if(x==1) cout<<0<<endl; else cout<<euler(x)<<endl; } }

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<queue> #include<string> #include<cmath> #include<map> using namespace std; typedef long long ll; // UVA10179 Irreducable // 多组数据,每组计算给定数的欧拉函数。 int euler(int x){ int ans=x; for(int i=2;i*i<=x;i++) if(x%i==0){ ans=ans/i*(i-1); while(x%i==0) x/=i; } if(x>1) ans=ans/x*(x-1); return ans; //返回ϕ(x)的值 } int main(){ int x; while(scanf("%d",&x)&&x) cout<<euler(x)<<endl; }

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<queue> #include<string> #include<cmath> #include<map> using namespace std; typedef long long ll; // poj2773 Happy 2006 //求第k个与n互素的数 // gcd(t×n+a,n)=gcd(a,n),所有与n互质的数都以phi(n)为周期。 ll euler(ll x){ ll ans=x; for(ll i=2;i*i<=x;i++) if(x%i==0){ ans=ans/i*(i-1); while(x%i==0) x/=i; } if(x>1) ans=ans/x*(x-1); return ans; //返回ϕ(x)的值 } ll gcd(ll a,ll b){ if(b==0) return a; else return gcd(b,a%b); } ll n,k,phi,p[1000019]; int main(){ while(scanf("%d%d",&n,&k)!=EOF){ phi=0; for(int i=1;i<=n;i++) if(gcd(i,n)==1) p[++phi]=i; printf("%d\n",p[(k-1)%phi+1]+(k-1)/phi*n); } }

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<queue> #include<string> #include<cmath> #include<map> using namespace std; typedef long long ll; // UVA12995 Farey Sequence //求欧拉函数的前缀和 // 求∑(i=2~n)ϕ(i),用欧拉函数的线性求法即可. const ll N=1000019; ll phi[N],vis[N],prime[N],p_num=0,n,sum[N]; void GetPhi(ll n){ //phi[1]=1; //特例:ϕ(1)=1; //此题=1时输出0 for(ll i=2;i<=n;i++){ if(!vis[i]) prime[++p_num]=i,phi[i]=i-1; //i是素数(1) sum[i]=sum[i-1]+phi[i]; //前缀和 for(ll j=1;j<=p_num&&i*prime[j]<=n;j++){ //枚举“i*质数” vis[i*prime[j]]=1; //标记“i*质数”为合数 if(i%prime[j]==0) //(3)注意这里可以直接break; {phi[i*prime[j]]=phi[i]*prime[j];break;} else phi[i*prime[j]]=phi[i]*(prime[j]-1); }//(2) } } int main(){ GetPhi(1000001); while(scanf("%lld",&n)&&n) printf("%lld\n",sum[n]); }

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<queue> #include<string> #include<cmath> #include<map> using namespace std; typedef long long ll; // SP5971 LCMSUM //欧拉函数求LCM的前缀和 // 答案为(1/2)*∑(d′|n)(d′×φ(d′)+n)。 // 预处理phi数组,再枚举每个约数去计算对所有倍数的贡献。 const ll N=1000019; ll phi[N],vis[N],prime[N],p_num=0,n,ans[N]; void GetPhi(ll n){ phi[1]=1; //特例:ϕ(1)=1; for(ll i=2;i<=n;i++){ if(!vis[i]) prime[++p_num]=i,phi[i]=i-1; //i是素数(1) for(ll j=1;j<=p_num&&i*prime[j]<=n;j++){ //枚举“i*质数” vis[i*prime[j]]=1; //标记“i*质数”为合数 if(i%prime[j]==0) //(3)注意这里可以直接break; {phi[i*prime[j]]=phi[i]*prime[j];break;} else phi[i*prime[j]]=phi[i]*(prime[j]-1); }//(2) } for(int i=1;i<=n;i++) //枚举因数i的所有倍数 for(int j=i;j<=n;j+=i) ans[j]+=i*phi[i]/2; for(int i=1;i<=n;i++) ans[i]=ans[i]*i+i; //处理公式中的+n } int main(){ GetPhi(1000001); int T; cin>>T; while(T--) scanf("%lld",&n),printf("%lld\n",ans[n]); }


#include <cmath> #include <iostream> #include <cstdio> #include <string> #include <cstring> #include <vector> #include <algorithm> #include <stack> #include <queue> #include <iomanip> using namespace std; typedef long long ll; typedef unsigned long long ull; // p1447 能量采集 //欧拉函数 + 数学计算 // 可以发现:(0,0)到(x,y)上的整数点个数(包括点(x,y))为gcd(x,y)。 // 那么答案为:2∑(gcd(i,j)-1)+nm=2∑gcd(i,j)-nm。 // 根据:https://images2015.cnblogs.com/blog/1078180/201706/1078180-20170613101314712-47533424.png // 可得:∑∑gcd(i,j) = ∑∑ ( ∑(d|gcd(i,j))*phi(d) ) [ 根据:∑(d|n)ϕ(d)=n ] // = ∑∑ ( ∑(d|i&d|j))*phi(d) ) = ... const int N=100019; int phi[N],vis[N],prime[N],tot=0; ll sum[N]; void GetPhi(int n){ phi[1]=sum[1]=1; //特例:ϕ(1)=1; for(int i=2;i<=n;i++){ if(!vis[i]) prime[++tot]=i,phi[i]=i-1; //i是素数(1) for(int j=1;j<=tot&&i*prime[j]<=n;j++){ //枚举“i*质数” vis[i*prime[j]]=1; //标记“i*质数”为合数 if(i%prime[j]==0) //(3)注意这里可以直接break; {phi[i*prime[j]]=phi[i]*prime[j];break;} else phi[i*prime[j]]=phi[i]*(prime[j]-1); } //(2) sum[i]=sum[i-1]+phi[i]; } } ll cal(int a,int b){ int lastt; ll ans=0; for(int i=1;i<=a&&i<=b;i=lastt+1) //调和级数の分块法 lastt=min(a/(a/i),b/(b/i)), //(快速确定相同的a/i和b/i的sum值) ans+=(ll)(sum[lastt]-sum[i-1])*(a/i)*(b/i); return ans; } int main(){ GetPhi(100001); int a,b; scanf("%d%d",&a,&b); printf("%lld\n",2*cal(a,b)-(ll)a*b); }
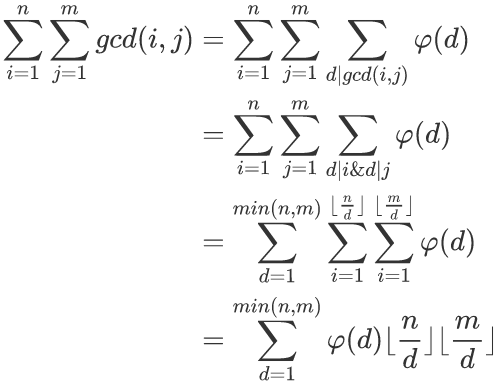
欧拉定理与相关习题
欧拉定理:
扩展欧拉定理:

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<queue> #include<string> #include<cmath> #include<map> using namespace std; typedef long long ll; // p5091 【模板】 扩展欧拉定理 // 求a^b mod m //【扩展欧拉定理】 b≥φ(m)时,a^b≡a^((bmodφ(m))+φ(m)) mod m ; int a,b,m,ans=1; bool flag; int euler(int x){ int ans=x; for(int i=2;i*i<=x;i++) if(x%i==0){ ans=ans/i*(i-1); while(x%i==0) x/=i; } if(x>1) ans=ans/x*(x-1); return ans; //返回ϕ(x)的值 } int main(){ char c; scanf("%d%d",&a,&m); int phi=euler(m); while(!isdigit(c=getchar())); //边读入b边取模 for(;isdigit(c);c=getchar()){ b=b*10+c-'0'; if(b>=phi) flag=true,b%=phi; } if(flag) b+=phi; //只有b>=phi时,公式才成立(否则不用+φ(m)) for(int i=20;i>=0;i--){ //ksm求a^((bmodφ(m))+φ(m)) ans=1ll*ans*ans%m; if(b&(1<<i)) ans=1ll*ans*a%m; } cout<<ans<<endl; return 0; }

// luogu-judger-enable-o2 // luogu-judger-enable-o2 #include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<queue> #include<string> #include<cmath> #include<map> using namespace std; typedef long long ll; // p4139 上帝与集合的正确用法 //扩展欧拉定理求2^(2^(2^(2...)))mod p // 【扩展欧拉定理】 b≥φ(p))时,a^b≡a^((bmodφ(p)))+φ(p))) mod p ; // 令f(p)=2^(2^(2^(2...))) mod p,则有f(p)=2^(f(φ(p))+φ(p)) mod p 。 const ll N=10000019; ll phi[N],prime[N],p_num=0,p; void GetPhi(ll n){ phi[1]=1; //特例:ϕ(1)=1; for(ll i=2;i<=n;i++){ if(!phi[i]) prime[++p_num]=i,phi[i]=i-1; //i是素数(1) for(ll j=1;j<=p_num&&i*prime[j]<=n;j++){ //枚举“i*质数” if(i%prime[j]==0) //(3)注意这里可以直接break; {phi[i*prime[j]]=phi[i]*prime[j];break;} else phi[i*prime[j]]=phi[i]*(prime[j]-1); }//(2) } } ll ksm(ll a,ll b,ll mod){ //快速幂 ll anss=1; while(b) anss=anss*(b&1?a:1)%mod, a=a*a%mod,b>>=1; return anss; } ll solve(ll p){ if(p==1) return 0; return ksm(2,solve(phi[p])+phi[p],p); } //递归求解函数 int main(){ GetPhi(10000001); int T; cin>>T; while(T--) scanf("%lld",&p),printf("%lld\n",solve(p)); }

#include <cmath> #include <iostream> #include <cstdio> #include <string> #include <cstring> #include <vector> #include <algorithm> #include <stack> #include <queue> #include <iomanip> using namespace std; typedef long long ll; typedef unsigned long long ull; //【uva10692】Huge Mods //欧拉定理 //计算a1^a2^a3^a4......^an模m的值。 //欧拉定理:(a^x)%m=(a^(x%phi(m)+phi(m))%m x>=phi(m) const int N=100019; int m,n,a[N]; char M[15]; int phi[N],vis[N],prime[N],tot=0; void GetPhi(int n){ phi[1]=1; //特例:ϕ(1)=1; for(int i=2;i<=n;i++){ if(!vis[i]) prime[++tot]=i,phi[i]=i-1; //i是素数(1) for(int j=1;j<=tot&&i*prime[j]<=n;j++){ //枚举“i*质数” vis[i*prime[j]]=1; //标记“i*质数”为合数 if(i%prime[j]==0) //(3)注意这里可以直接break; {phi[i*prime[j]]=phi[i]*prime[j];break;} else phi[i*prime[j]]=phi[i]*(prime[j]-1); }//(2) } } int pow_mod(int x,int k,int mod){ int now=1; for(int i=0;i<k;i++){ if(x==1) break; now*=x; if(now>=mod) break; } if(now>=mod) now=mod; else now=0; if(k==0) return 1; int ans=pow_mod(x*x%mod,k>>1,mod); if(k&1) ans=ans*x%mod; return ans+now; } int dfs(int i,int mod){ if(i==n-1){ if(a[i]>=mod) return a[i]%mod+mod; return a[i]; } int k=dfs(i+1,phi[mod]); return pow_mod(a[i],k,mod); } int main() { GetPhi(100001); int kase=0; while(~scanf("%s",M)&&M[0]!='#'){ sscanf(M,"%d",&m); scanf("%d",&n); for(int i=0;i<n;i++) scanf("%d",&a[i]); printf("Case #%d: %d\n",++kase,dfs(0,m)%m); } }

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<string> #include<queue> #include<map> #include<vector> #include<cmath> using namespace std; typedef long long ll; /*【p3747】相逢是问候 */ //【标签】欧拉函数 + 线段树 + 极限标记思想(还是过不了...) void reads(ll &x){ //读入优化(正负整数) ll fx=1;x=0;char ch_=getchar(); while(ch_<'0'||ch_>'9'){if(ch_=='-')fx=-1;ch_=getchar();} while(ch_>='0'&&ch_<='9'){x=x*10+ch_-'0';ch_=getchar();} x*=fx; //正负号 } const ll N=500019,max_phi=150019; ll n,m,p,c,a[N+10],primes[N+10],p_cnt,phi[59],PHI_=0; bool vis_[N+10],f; ll ksm(ll a,ll b,ll p){ ll anss=1; while(b>0){ if(b&1) anss=anss*a; a=a*a,b>>=1; if(a>=p) f=1,a%=p; if(anss>=p) f=1,anss%=p; } return anss; } ll C(ll a,ll x){ ll tmp=a; if(tmp>phi[x]) tmp=tmp%phi[x]+phi[x]; for(ll i=x;i>0;i--){ f=0,tmp=ksm(c,tmp,phi[i-1]); if(f==1) tmp+=phi[i-1],f=0; } return tmp; } //-------------线段树---------------// struct tree{ ll l,r,tag,sum; }seg[N<<2]; void update(ll rt){ //tag:维护每个区间整体(最少)被修改了多少次 seg[rt].sum=seg[rt<<1].sum+seg[rt<<1|1].sum; seg[rt].tag=min(seg[rt<<1].tag,seg[rt<<1|1].tag); } void build(ll rt,ll l,ll r){ seg[rt].l=l,seg[rt].r=r; if(l==r){ seg[rt].sum=a[l]; return; } ll mid=(l+r)>>1; build(rt<<1,l,mid),build(rt<<1|1,mid+1,r),update(rt); } void change(ll rt,ll L,ll R){ //每次直接暴力修改,记区间最小标记次数tag,>=PHI_就不改了 if(seg[rt].tag>=PHI_) return; ll l=seg[rt].l,r=seg[rt].r; if(l==r){ seg[rt].sum=C(a[l],++seg[rt].tag)%p; return; } ll mid=(l+r)>>1; if(L<=mid) change(rt<<1,L,R); if(R>mid) change(rt<<1|1,L,R); update(rt); } //单点修改 ll query(ll rt,ll L,ll R){ ll l=seg[rt].l,r=seg[rt].r; if(r<L||l>R) return 0; if(L<=l&&R>=r) return seg[rt].sum%p; return (query(rt<<1,L,R)+query(rt<<1|1,L,R))%p; } //--------------欧拉部分---------------// ll Phi(ll x){ ll ans=x; //求欧拉函数 for(ll i=1;i<=p_cnt&&primes[i]*primes[i]<=x;i++){ if(!(x%primes[i])) ans=ans/primes[i]*(primes[i]-1); while(!(x%primes[i])) x/=primes[i]; } if(x>1) ans=ans/x*(x-1); return ans; } void get_prime(){ //欧拉筛素数 for(ll i=2;i<=max_phi;i++){ if(!vis_[i]) primes[++p_cnt]=i; for(ll j=1;j<=p_cnt;j++) { if(i*primes[j]>max_phi) break; vis_[i*primes[j]]=1; if(i%primes[j]==0) break; } } phi[PHI_]=p; while(phi[PHI_]!=1) phi[++PHI_]=Phi(phi[PHI_-1]); phi[++PHI_]=1; } //---------------主程序-----------------// int main(){ reads(n),reads(m),reads(p),reads(c); for(ll i=1;i<=n;i++) reads(a[i]); get_prime(); build(1,1,n); for(ll i=1,op,l,r;i<=m;i++){ reads(op),reads(l),reads(r); if(op==0) change(1,l,r); //区间替换为c^ai if(op==1) printf("%lld\n",query(1,l,r)%p); } }
综合练习题系列

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<string> #include<queue> #include<vector> #include<cmath> #include<map> using namespace std; typedef long long ll; //【p2155】莎拉公主的困惑 //列出式子,可以发现:ans = (n!/m!) * m!*∏(i=1~k)pi/pi−1 (欧拉函数的定义) void reads(int &x){ //读入优化(正负整数) int fx=1;x=0;char s=getchar(); while(s<'0'||s>'9'){if(s=='-')fx=-1;s=getchar();} while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+s-'0';s=getchar();} x*=fx; //正负号 } const int N=10000019,M=800019; bool vis_[N]; int jc[N],inv[N],ans[N],primes[M],tot=0,mod; inline void init(int MAXN){ jc[0]=jc[1]=1,inv[0]=inv[1]=1,ans[0]=ans[1]=1; for(register int i=2;i<=MAXN;i++){ //线性求阶乘&逆元数组 jc[i]=1LL*jc[i-1]*i%mod,inv[i]=1LL*(mod-mod/i)*inv[mod%i]%mod; if(!vis_[i]) primes[++tot]=i; //筛质数 for(register int j=1;j<=tot&&i*primes[j]<=MAXN;j++) { vis_[i*primes[j]]=1; if(i%primes[j]==0) break; } //剪枝优化 } for(register int i=2;i<=MAXN;i++){ ans[i]=ans[i-1]; //ans:阶乘i!的∏(i=1~k)pi/pi−1 if(!vis_[i]) ans[i]=1LL*ans[i]*(i-1)%mod*inv[i]%mod; } } //每次*质因子 int main(){ int T,n,m; reads(T),reads(mod); init(N-10); while(T--) reads(n),reads(m),printf("%lld\n",1LL*jc[n]*ans[m]%mod); } //利用阶乘m!的所有质因子都是1~n线性单调出现的,直接将每个质因子连乘即可 //很神奇的一点是,开了LL真的超级耗时...就一个LL就会TLE两个点,还基本都是900ms+...
——时间划过风的轨迹,那个少年,还在等你





 浙公网安备 33010602011771号
浙公网安备 33010602011771号