【暖*墟】#网络流# 最大流与最小割
- "最小的割边"(最小割):
使原点S和汇点T不连通,最少要割几条边。 - "最小的割点":
使原点S和汇点T不连通,最少要割几个点。
【 最小割(最小的割边)= 最大流 】
当达到最大流时,根据增广路定理,残留网络中s到t已经没有通路了。
我们把s能到的的点集设为S,不能到的点集为T,
构造出一个割集C[S,T],S到T的边必然满流,否则就能继续增广。
这些满流边的流量和就是当前的流即最大流。
把这些满流边作为割,就构造出了一个和最大流相等的割。
那么此时就构造出一个流等于一个割,即最大流=最小割。
【 求 “ 最小的割点 ”】
我们可以通过转化,把最小的割点转为最小的割边。
假设原来的点编号为i,总共有n个点,那么我们就把每个点拆成两个点,编号分别为i和i+n。
其中点 i 负责连接原图中连入这个点的边,点 i+n 负责连原图中连出这个点的边。
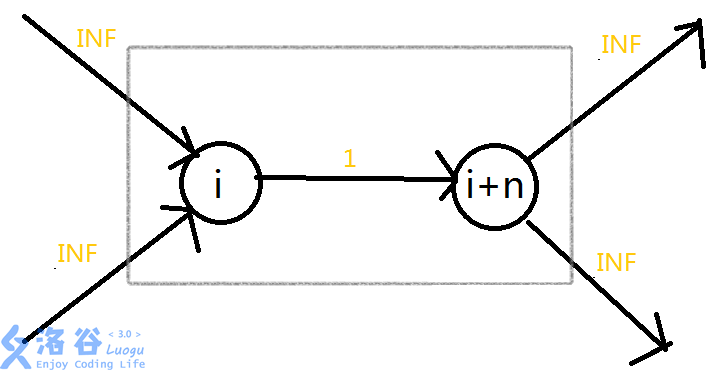
即:我们可以考虑“拆点”,即把一个点拆成两个点,中间连一条边权为1的边。
前一个点作为“入点”,别的点连边连入这里;后一个点作为“出点”,出去的边从这里出去。
这样,只要我们切断中间那条边,就可以等效于除去这个点。
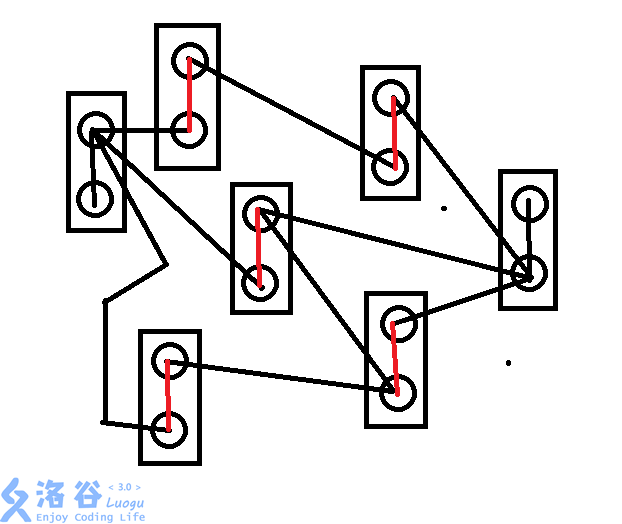
红色的边边权为1(可断),黑色的边边权为inf(不能删除的点,必须要选择)。
原点和汇点的内部边权为inf,因为显然这两个点不能删除。
for(int i=1;i<=n;i++) add(i,i+n,1),add(i+n,i,0); //拆点 for(int i=1,u,v;i<=m;i++) reads(u),reads(v), add(u+n,v,(1<<30)),add(v,u+n,0), //从此点的分点2 add(v+n,u,(1<<30)),add(u,v+n,0); //连向其它点的分点1 s=s+n; dinic(); //注意起点的设置,起点+n、或者终点+n(差别大)
【代码の相关注意事项】
1.head数组的清零:若 tot=-1 开始,则每次要 memset(head,-1,sizeof(head));
若 tot=1 开始,则有多组数据时,要 memset(head,0,sizeof(head));
(注意:tot!=0,是为了方便dfs函数中的 e[i].w-=f,e[i^1].w+=f; 操作 )
2.拆点的编号:注意 起点、终点的设置 和 边的连向性顺序。

#include <cmath> #include <iostream> #include <cstdio> #include <string> #include <cstring> #include <vector> #include <algorithm> #include <queue> #include <stack> using namespace std; typedef long long ll; typedef unsigned long long ull; #define R register /*【p3145】奶牛的电信 [最小的割点-模板] */ void reads(int &x){ //读入优化(正负整数) int f=1;x=0;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} x*=f; //正负号 } const int N=50019; int s,t,tot=1,n,m,ans,head[N],dep[N]; //s为源点,t为汇点 struct node{ int nextt,ver,w; }e[N]; void add(int x,int y,int z) { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,head[x]=tot; } bool bfs(){ memset(dep,0,sizeof(dep)); //dep记录深度 queue<int> q; while(!q.empty()) q.pop(); dep[s]=1; q.push(s); while(!q.empty()){ int u=q.front(); q.pop(); for(int i=head[u];i;i=e[i].nextt) if((e[i].w>0)&&(dep[e[i].ver]==0)) //分层 dep[e[i].ver]=dep[u]+1,q.push(e[i].ver); } if(dep[t]!=0) return 1; else return 0; //此时不存在分层图也不存在增广路 } int dfs(int u,int lastt){ if(u==t) return lastt; //lastt:此点还剩余的流量 for(int i=head[u];i;i=e[i].nextt) if((dep[e[i].ver]==dep[u]+1)&&(e[i].w!=0)){ int f=dfs(e[i].ver,min(lastt,e[i].w)); if(f>0){ e[i].w-=f,e[i^1].w+=f; return f; } } return 0; //没有dfs>0即说明没有增广路,返回0 } void dinic(){ ans=0; while(bfs()) ans+=dfs(s,(1<<30)); } int main(){ reads(n),reads(m),reads(s),reads(t); //↓↓拆点 for(int i=1;i<=n;i++) add(i,i+n,1),add(i+n,i,0); for(int i=1,u,v;i<=m;i++) reads(u),reads(v), //从分点2连向其余电脑的 add(u+n,v,(1<<30)),add(v,u+n,0),add(v+n,u,(1<<30)),add(u,v+n,0); s=s+n; dinic(); cout<<ans<<endl; //注意:起点要变成s+n }

#include <cmath> #include <iostream> #include <cstdio> #include <string> #include <cstring> #include <vector> #include <algorithm> #include <queue> #include <stack> using namespace std; typedef long long ll; typedef unsigned long long ull; #define R register /*【uva1660】电视网络 [最小的割点-模板] */ void reads(int &x){ //读入优化(正负整数) int f=1;x=0;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} x*=f; //正负号 } const int N=50019; int s,t,tot=1,n,m,ans,head[N],dep[N]; //s为源点,t为汇点 struct node{ int nextt,ver,w; }e[N],edge[N]; void add(int x,int y,int z) { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,head[x]=tot; } bool bfs(){ memset(dep,0,sizeof(dep)); //dep记录深度 queue<int> q; while(!q.empty()) q.pop(); dep[s]=1; q.push(s); while(!q.empty()){ int u=q.front(); q.pop(); for(int i=head[u];i;i=edge[i].nextt) if((edge[i].w>0)&&(dep[edge[i].ver]==0)) //分层 dep[edge[i].ver]=dep[u]+1,q.push(edge[i].ver); } if(dep[t]!=0) return 1; else return 0; //此时不存在分层图也不存在增广路 } int dfs(int u,int lastt){ if(u==t) return lastt; //lastt:此点还剩余的流量 for(int i=head[u];i;i=edge[i].nextt) if((dep[edge[i].ver]==dep[u]+1)&&(edge[i].w!=0)){ int f=dfs(edge[i].ver,min(lastt,edge[i].w)); if(f>0){ edge[i].w-=f,edge[i^1].w+=f; return f; } } return 0; //没有dfs>0即说明没有增广路,返回0 } void dinic(){ ans=0; while(bfs()) ans+=dfs(s,(1<<30)); } int main(){ while(scanf("%d%d",&n,&m)!=EOF){ if(n==0){ puts("0"); continue; } if(n==1){ puts("1"); continue; } if(m==0){ puts("0"); continue; } memset(head,0,sizeof(head)); memset(dep,0,sizeof(dep)); tot=1; for(int i=1;i<=n;i++) add(i,i+n,1),add(i+n,i,0); for(int i=1,u,v;i<=m;i++) reads(u),reads(v),u++,v++, add(u+n,v,(1<<30)),add(v,u+n,0),add(v+n,u,(1<<30)),add(u,v+n,0); int anss=n; for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++){ //枚举起点、终点 for(int k=0;k<=tot;k++) edge[k]=e[k]; //复制 edge[(i<<1)].w=(1<<30),edge[(j<<1)].w=(1<<30); s=i,t=j+n; dinic(); anss=min(anss,ans); } cout<<anss<<endl; //(未确定起点终点的)最小割点数 } }

// luogu-judger-enable-o2 #include <cmath> #include <iostream> #include <cstdio> #include <string> #include <cstring> #include <vector> #include <algorithm> #include <queue> #include <stack> using namespace std; typedef long long ll; typedef unsigned long long ull; #define R register //这题真神奇...一下RE一下WA...莫名其妙要开LL...开了LL还要加大数组... /*【p3931】SAC 割开一棵树,让所有的[叶节点]和[根节点]都不连通,求min代价。*/ //【最小割问题】源点S为根节点,汇点不止一个,怎么办呢? //---> 找一个“超级汇点”(所有的汇点都汇聚到这个点上,流量为inf)即可。 void reads(ll &x){ //读入优化(正负整数) ll f=1;x=0;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} x*=f; //正负号 } const ll N=500019; ll leaf[N]; //连边数(即无向图的度) ll s,t,tot=1,n,ans,head[N],dep[N]; //s为源点,t为汇点 struct node{ ll nextt,ver,w; }e[N]; void add(ll x,ll y,ll z) { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,head[x]=tot; } bool bfs(){ memset(dep,0,sizeof(dep)); //dep记录深度 queue<ll> q; while(!q.empty()) q.pop(); dep[s]=1; q.push(s); while(!q.empty()){ ll u=q.front(); q.pop(); for(ll i=head[u];i;i=e[i].nextt) if((e[i].w>0)&&(dep[e[i].ver]==0)) //分层 dep[e[i].ver]=dep[u]+1,q.push(e[i].ver); } if(dep[t]!=0) return 1; else return 0; //此时不存在分层图也不存在增广路 } ll dfs(ll u,ll lastt){ if(u==t) return lastt; //lastt:此点还剩余的流量 for(ll i=head[u];i;i=e[i].nextt) if((dep[e[i].ver]==dep[u]+1)&&(e[i].w!=0)){ ll f=dfs(e[i].ver,min(lastt,e[i].w)); if(f>0){ e[i].w-=f,e[i^1].w+=f; return f; } } return 0; //没有dfs>0即说明没有增广路,返回0 } void dinic(){ ans=0; while(bfs()) ans+=dfs(s,1e12); } int main(){ reads(n),reads(s); for(ll i=1,a,b,c;i<n;i++) reads(a),reads(b),reads(c), add(a,b,c),add(b,a,c),leaf[a]++,leaf[b]++; for(ll i=1;i<=n;i++) //寻找叶子节点 ↓↓此处n+1为超级汇点 if(leaf[i]==1&&i!=s) add(n+1,i,1e12),add(i,n+1,1e12); t=n+1; dinic(); cout<<ans<<endl; //注意:终点要变成n+1 }
【相关问题模型】

即:若问题模型满足二者选其一的性质,我们可以考虑用最小割来解决。

// luogu-judger-enable-o2 // luogu-judger-enable-o2 #include <cmath> #include <iostream> #include <cstdio> #include <string> #include <cstring> #include <vector> #include <algorithm> #include <queue> #include <stack> using namespace std; typedef long long ll; typedef unsigned long long ull; #define R register //p1361 小M的作物 //按照问题模型建图 + 建虚点 /*【p1361】小M的作物 n个物品可以选择A、B两地种植,价值分别为ai、bi。 有M种组合方案,种在同一地点可以获得额外收益。*/ //【最小割问题】单独的作物直接向S、T连边。每个组合是一个点集。 //每个点集的贡献:对A;对B;没有贡献。显然每个点集必须用一个虚点代替。 //先将此虚点连向S,如果组合中的一个点被割进了集合B,虚点--S这条边就要断开。 //具体来说,边(S,x)的容量为ci,边(x,u),(x,v),...,(x,w)的容量均为INF(无损失)。 //对B同理。 void reads(int &x){ //读入优化(正负整数) int f=1;x=0;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} x*=f; //正负号 } const int M=5000019,N=3019; int a[N],b[N]; int s,t,tot=1,n,m,ans,head[N],dep[N],cur[N]; //s为源点,t为汇点 struct node{ int nextt,ver,w; }e[M]; void add(int x,int y,int z) { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,head[x]=tot; } bool bfs(){ memset(dep,0,sizeof(dep)); //dep记录深度 memcpy(cur,head,sizeof(head)); queue<int> q; while(!q.empty()) q.pop(); dep[s]=1; q.push(s); while(!q.empty()){ int u=q.front(); q.pop(); for(int i=head[u];i;i=e[i].nextt) if((e[i].w>0)&&(dep[e[i].ver]==0)) //分层 dep[e[i].ver]=dep[u]+1,q.push(e[i].ver); } if(dep[t]!=0) return 1; else return 0; //此时不存在分层图也不存在增广路 } int dfs(int u,int lastt){ int cnt=0; if(u==t) return lastt; //lastt:此点还剩余的流量 for(int i=cur[u];i&&cnt<lastt;i=e[i].nextt){ cur[u]=i; //当前弧优化 if((dep[e[i].ver]==dep[u]+1)&&(e[i].w!=0)){ int f=dfs(e[i].ver,min(lastt-cnt,e[i].w)); if(f>0){ e[i].w-=f,e[i^1].w+=f; cnt+=f; } } } if(cnt<lastt) dep[u]=-1; return cnt; } void dinic(){ ans=0; while(bfs()) ans+=dfs(s,2e9); } int id(int typ,int i){ if(typ==1) return i; if(typ==2) return m+i; if(typ==3) return m+n+i; } int main(){ reads(n); int anss=0; for(int i=1;i<=n;i++) reads(a[i]),anss+=a[i]; for(int i=1;i<=n;i++) reads(b[i]),anss+=b[i]; reads(m); s=0,t=n+m+m+1; //n个作物,2*m个虚点(每个组合向S、T连边的点) for(int i=1;i<=n;i++) add(s,id(2,i),a[i]),add(id(2,i),s,0), add(id(2,i),t,b[i]),add(t,id(2,i),0); for(int i=1,k,c1,c2,x;i<=m;i++){ reads(k),reads(c1),reads(c2),anss+=c1+c2; //种在A中c1,种在B中C2 while(k--) reads(x),add(id(1,i),id(2,x),2e9),add(id(2,x),id(1,i),0), add(id(2,x),id(3,i),2e9),add(id(3,i),id(2,x),0); add(s,id(1,i),c1),add(id(1,i),s,0),add(id(3,i),t,c2),add(t,id(3,i),0); } dinic(); cout<<anss-ans<<endl; //答案=总收益-最小割(=最大流) }

#include <cmath> #include <iostream> #include <cstdio> #include <string> #include <cstring> #include <vector> #include <algorithm> #include <queue> #include <stack> using namespace std; typedef long long ll; typedef unsigned long long ull; #define R register //p2057 善意的投票 //最小割模型相关问题的建图方式 /*【p2057】善意的投票 有n个人、两种不同的意见、并且有许多对朋友, 需要让朋友间尽可能的统一意见(少发生冲突), 如果一个人违反自己的本意也算冲突,求最少的冲突。*/ //【最小割问题】割最少的边使得ST成为两个不同的集合,即最小割。 //将S连向同意的人,T连向不同意的人,若两人是朋友,则在他们之间连一条双向边。 //Q:为什么是双向边? A:若两个人有冲突,则只需要其中任意一个人改变意见就行了, //让a同意b的意见或者b同意a的意见(两种情况,建双向边),割掉一条边、满足一种情况即可。 void reads(int &x){ //读入优化(正负整数) int f=1;x=0;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} x*=f; //正负号 } const int M=5000019,N=3019; int a[N],b[N]; int s,t=519,tot=1,n,m,ans,head[N],dep[N],cur[N]; //s为源点,t为汇点 struct node{ int nextt,ver,w; }e[M]; void add(int x,int y,int z) { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,head[x]=tot; } bool bfs(){ memset(dep,0,sizeof(dep)); //dep记录深度 memcpy(cur,head,sizeof(head)); queue<int> q; while(!q.empty()) q.pop(); dep[s]=1; q.push(s); while(!q.empty()){ int u=q.front(); q.pop(); for(int i=head[u];i;i=e[i].nextt) if((e[i].w>0)&&(dep[e[i].ver]==0)) //分层 dep[e[i].ver]=dep[u]+1,q.push(e[i].ver); } if(dep[t]!=0) return 1; else return 0; //此时不存在分层图也不存在增广路 } int dfs(int u,int lastt){ int cnt=0; if(u==t) return lastt; //lastt:此点还剩余的流量 for(int i=cur[u];i&&cnt<lastt;i=e[i].nextt){ cur[u]=i; //当前弧优化 if((dep[e[i].ver]==dep[u]+1)&&(e[i].w!=0)){ int f=dfs(e[i].ver,min(lastt-cnt,e[i].w)); if(f>0){ e[i].w-=f,e[i^1].w+=f; cnt+=f; } } } if(cnt<lastt) dep[u]=-1; return cnt; } void dinic(){ ans=0; while(bfs()) ans+=dfs(s,2e9); } int main(){ reads(n); reads(m); for(int i=1,x;i<=n;i++){ reads(x); if(x==1) add(s,i,1),add(i,s,0); else add(i,t,1),add(t,i,0); } for(int i=1,x,y;i<=m;i++) reads(x),reads(y),add(x,y,1),add(y,x,1); dinic(); cout<<ans<<endl; //答案=最小割(=最大流) }

#include <cmath> #include <iostream> #include <cstdio> #include <string> #include <cstring> #include <vector> #include <algorithm> #include <queue> #include <stack> using namespace std; typedef long long ll; typedef unsigned long long ull; #define R register //p1344 追查坏牛奶 //最小割模板 + 巧妙求删边数 /*【p1344】追查坏牛奶 给出边的权值,要求最小的代价使得1和n不连通。*/ //【如何求最小割の删边数】每边边权+1,求最小割’,删边数=最小割’-最小割。 // 详见 https://83564.blog.luogu.org/solution-p1344 某dalao qwq void reads(int &x){ //读入优化(正负整数) int f=1;x=0;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} x*=f; //正负号 } const int N=5019; int x[N],y[N],z[N]; int s,t,tot=1,n,m,ans,anss,head[N],dep[N],cur[N]; //s为源点,t为汇点 struct node{ int nextt,ver,w; }e[N*4]; void add(int x,int y,int z) { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,head[x]=tot; } bool bfs(){ memset(dep,0,sizeof(dep)); //dep记录深度 memcpy(cur,head,sizeof(head)); queue<int> q; while(!q.empty()) q.pop(); dep[s]=1; q.push(s); while(!q.empty()){ int u=q.front(); q.pop(); for(int i=head[u];i;i=e[i].nextt) if((e[i].w>0)&&(dep[e[i].ver]==0)) //分层 dep[e[i].ver]=dep[u]+1,q.push(e[i].ver); } if(dep[t]!=0) return 1; else return 0; //此时不存在分层图也不存在增广路 } int dfs(int u,int lastt){ int cnt=0; if(u==t) return lastt; //lastt:此点还剩余的流量 for(int i=cur[u];i&&cnt<lastt;i=e[i].nextt){ cur[u]=i; //当前弧优化 if((dep[e[i].ver]==dep[u]+1)&&(e[i].w!=0)){ int f=dfs(e[i].ver,min(lastt-cnt,e[i].w)); if(f>0){ e[i].w-=f,e[i^1].w+=f; cnt+=f; } } } if(cnt<lastt) dep[u]=-1; return cnt; } void dinic(){ ans=0; while(bfs()) ans+=dfs(s,2e9); } int main(){ reads(n); reads(m); s=1,t=n; for(int i=1;i<=m;i++){ reads(x[i]),reads(y[i]),reads(z[i]), add(x[i],y[i],z[i]),add(y[i],x[i],0); } dinic(); anss=ans; cout<<ans<<" "; //答案1=最小割(=最大流) ans=0,memset(head,0,sizeof(head)),tot=1; for(int i=1;i<=m;i++) add(x[i],y[i],z[i]+1),add(y[i],x[i],0); dinic(); cout<<ans-anss<<endl; //答案2=删边数 }

#include <cmath> #include <iostream> #include <cstdio> #include <string> #include <cstring> #include <vector> #include <algorithm> #include <queue> #include <stack> using namespace std; typedef long long ll; typedef unsigned long long ull; #define R register //p4001 狼抓兔子 //最小割 + 图形式连边 void reads(int &x){ //读入优化(正负整数) int f=1;x=0;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} x*=f; //正负号 } const int N=1000019; int s,t,tot=1,n,m,ans,head[N],dep[N],cur[N]; //s为源点,t为汇点 struct node{ int nextt,ver,w; }e[N*6]; void add(int x,int y,int z) { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,head[x]=tot; } bool bfs(){ memset(dep,0,sizeof(dep)); //dep记录深度 memcpy(cur,head,sizeof(head)); queue<int> q; while(!q.empty()) q.pop(); dep[s]=1; q.push(s); while(!q.empty()){ int u=q.front(); q.pop(); for(int i=head[u];i;i=e[i].nextt) if((e[i].w>0)&&(dep[e[i].ver]==0)) //分层 dep[e[i].ver]=dep[u]+1,q.push(e[i].ver); } if(dep[t]!=0) return 1; else return 0; //此时不存在分层图也不存在增广路 } int dfs(int u,int lastt){ int cnt=0; if(u==t) return lastt; //lastt:此点还剩余的流量 for(int i=cur[u];i&&cnt<lastt;i=e[i].nextt){ cur[u]=i; //当前弧优化 if((dep[e[i].ver]==dep[u]+1)&&(e[i].w!=0)){ int f=dfs(e[i].ver,min(lastt-cnt,e[i].w)); if(f>0){ e[i].w-=f,e[i^1].w+=f; cnt+=f; } } } if(cnt<lastt) dep[u]=-1; return cnt; } void dinic(){ ans=0; while(bfs()) ans+=dfs(s,2e9); } int id(int i,int j){ return (i-1)*m+j; } int main(){ reads(n); reads(m); s=1,t=id(n,m); for(int i=1;i<=n;i++) //(1) for(int j=1;j<m;j++){ int x; reads(x); add(id(i,j),id(i,j+1),x),add(id(i,j+1),id(i,j),x); } for(int i=1;i<n;i++) //(2) for(int j=1;j<=m;j++){ int x; reads(x); add(id(i,j),id(i+1,j),x),add(id(i+1,j),id(i,j),x); } for(int i=1;i<n;i++) //(3) for(int j=1;j<m;j++){ int x; reads(x); add(id(i,j),id(i+1,j+1),x),add(id(i+1,j+1),id(i,j),x); } dinic(); cout<<ans<<endl; //答案=最小割(=最大流) }

#include <cmath> #include <iostream> #include <cstdio> #include <string> #include <cstring> #include <vector> #include <algorithm> #include <queue> #include <stack> using namespace std; typedef long long ll; typedef unsigned long long ull; #define R register /*【p4177】Order // 最小割【最大权闭合子图】 + 思路转化 有N个工作,M种机器,每个工作包括若干道工序,每道工序需要某种机器来完成。 你可以通过购买或租用机器来完成工序。现在给出这些参数,求最大利润。*/ /*【分析】如果你忘记了 最大权闭合子图 请左转 https://www.cnblogs.com/dilthey/p/7565206.html 如果不能租用机器,就是普通的最大权闭合图。最大权闭合子图 的 具体建图方式是: S向工作连容量为利润的边,工作向机器连容量为inf的边, 机器向T连容量为费用的边,答案为(sum_+)-mincut。 如果能租用机器怎么办?注意,最大权闭合图求法中边容量为inf,目的是防止割断该边。 本题中可以工作与机器之间的边,即,边容量不为inf,而是租用机器的费用。 */ void reads(int &x){ //读入优化(正负整数) int f=1;x=0;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} x*=f; //正负号 } const int N=5000019; int sum=0; //[最大权闭合子图]的正权和 int s,t,tot=1,n,m,ans,anss,head[N],dep[N],cur[N]; //s为源点,t为汇点 struct node{ int nextt,ver,w; }e[N]; void add(int x,int y,int z) { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,head[x]=tot; } bool bfs(){ memset(dep,0,sizeof(dep)); //dep记录深度 memcpy(cur,head,sizeof(head)); queue<int> q; while(!q.empty()) q.pop(); dep[s]=1; q.push(s); while(!q.empty()){ int u=q.front(); q.pop(); for(int i=head[u];i;i=e[i].nextt) if((e[i].w>0)&&(dep[e[i].ver]==0)) //分层 dep[e[i].ver]=dep[u]+1,q.push(e[i].ver); } if(dep[t]!=0) return 1; else return 0; //此时不存在分层图也不存在增广路 } int dfs(int u,int lastt){ int cnt=0; if(u==t) return lastt; //lastt:此点还剩余的流量 for(int i=cur[u];i&&cnt<lastt;i=e[i].nextt){ cur[u]=i; //当前弧优化 if((dep[e[i].ver]==dep[u]+1)&&(e[i].w!=0)){ int f=dfs(e[i].ver,min(lastt-cnt,e[i].w)); if(f>0){ e[i].w-=f,e[i^1].w+=f; cnt+=f; } } } if(cnt<lastt) dep[u]=-1; return cnt; } void dinic(){ ans=0; while(bfs()) ans+=dfs(s,2e9); } int main(){ reads(n); reads(m); s=0,t=n+m+1; for(int i=1,k,ai,pi,ci;i<=n;i++){ reads(ai),reads(k); add(s,i,ai),add(i,s,0),sum+=ai; //工作 while(k--) reads(pi),reads(ci),add(i,pi+n,ci),add(pi+n,i,0); //机器 } for(int i=1,ci;i<=m;i++) reads(ci),add(i+n,t,ci),add(t,i+n,0); dinic(); cout<<sum-ans<<endl; return 0; // ↑↑ 机器费用连向终点 }

#include <cmath> #include <iostream> #include <cstdio> #include <string> #include <cstring> #include <vector> #include <algorithm> #include <queue> #include <stack> using namespace std; typedef long long ll; typedef unsigned long long ull; #define R register /*【p4313】文理分科 // 最小割 + 思路转化 */ /*【分析】添加“组合”这个元素,即:把每个(i,j)得到same_的情况看成一个组合。 1. S向每个学生连边,容量为理科收益;每个学生向T连边,容量为文科收益。 2. 将‘组合’拆成两点,S与第一个连边,cap=全文科收益;“组合”向学生连inf的边; 组合中的学生向第二个组合点连inf的边;第二个向T连边,容量为全理科收益。*/ void reads(int &x){ //读入优化(正负整数) int f=1;x=0;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} x*=f; //正负号 } const int N=500019,inf=(int)2e9; int sum=0; //总权和 int s,t,tot=1,n,m,ans,anss,head[N],dep[N],cur[N]; //s为源点,t为汇点 struct node{ int nextt,ver,w; }e[N*4]; void add(int x,int y,int z) { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,head[x]=tot; e[++tot].ver=x,e[tot].nextt=head[y],e[tot].w=0,head[y]=tot; } bool bfs(){ memset(dep,0,sizeof(dep)); //dep记录深度 memcpy(cur,head,sizeof(head)); queue<int> q; while(!q.empty()) q.pop(); dep[s]=1; q.push(s); while(!q.empty()){ int u=q.front(); q.pop(); for(int i=head[u];i;i=e[i].nextt) if((e[i].w>0)&&(dep[e[i].ver]==0)) //分层 dep[e[i].ver]=dep[u]+1,q.push(e[i].ver); } if(dep[t]!=0) return 1; else return 0; //此时不存在分层图也不存在增广路 } int dfs(int u,int lastt){ int cnt=0; if(u==t) return lastt; //lastt:此点还剩余的流量 for(int i=cur[u];i&&cnt<lastt;i=e[i].nextt){ cur[u]=i; //当前弧优化 if((dep[e[i].ver]==dep[u]+1)&&(e[i].w!=0)){ int f=dfs(e[i].ver,min(lastt-cnt,e[i].w)); if(f>0){ e[i].w-=f,e[i^1].w+=f; cnt+=f; } } } if(cnt<lastt) dep[u]=-1; return cnt; } void dinic(){ ans=0; while(bfs()) ans+=dfs(s,inf); } int main(){ reads(n); reads(m); s=0,t=3*n*m+1; // S--组合1--学生--组合2--T for(int i=1,aij;i<=n*m;i++) reads(aij),add(s,i,aij),sum+=aij; //文 for(int i=1,bij;i<=n*m;i++) reads(bij),add(i,t,bij),sum+=bij; //理 for(int i=1,x;i<=n*m;i++){ //编号:学生;组合1;组合2 reads(x),add(s,i+n*m,x),add(i+n*m,i,inf),sum+=x; if(i%m!=0) add(i+n*m,i+1,inf); //右边 if(i%m!=1) add(i+n*m,i-1,inf); //左边 if(i>m) add(i+n*m,i-m,inf); //上面 if(i<=(n-1)*m) add(i+n*m,i+m,inf); //下面 } for(int i=1,x;i<=n*m;i++){ reads(x),add(i+2*n*m,t,x),add(i,i+2*n*m,inf),sum+=x; if(i%m!=0) add(i+1,i+2*n*m,inf); //右边 if(i%m!=1) add(i-1,i+2*n*m,inf); //左边 if(i>m) add(i-m,i+2*n*m,inf); //上面 if(i<=(n-1)*m) add(i+m,i+2*n*m,inf); //下面 } dinic(); cout<<sum-ans<<endl; return 0; //min_cut }

#include <cmath> #include <iostream> #include <cstdio> #include <string> #include <cstring> #include <vector> #include <algorithm> #include <queue> #include <stack> using namespace std; typedef long long ll; typedef unsigned long long ull; #define R register /*【uva13020】Landscaping // 最小割 + [神奇的建图方式]网格图关系转化 */ // 题意见:https://www.cnblogs.com/GXZlegend/p/6867393.html /*【分析】S->高地,容量为B;低地->T,容量为B;x->与x相邻的点,容量为A。*/ void reads(int &x){ //读入优化(正负整数) int f=1;x=0;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} x*=f; //正负号 } const int N=500019,inf=(int)2e9; int s,t,tot=1,n,m,ans,anss,head[N],dep[N],cur[N]; //s为源点,t为汇点 struct node{ int nextt,ver,w; }e[N*4]; void add(int x,int y,int z) { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,head[x]=tot; e[++tot].ver=x,e[tot].nextt=head[y],e[tot].w=0,head[y]=tot; } bool bfs(){ memset(dep,0,sizeof(dep)); //dep记录深度 memcpy(cur,head,sizeof(head)); queue<int> q; while(!q.empty()) q.pop(); dep[s]=1; q.push(s); while(!q.empty()){ int u=q.front(); q.pop(); for(int i=head[u];i;i=e[i].nextt) if((e[i].w>0)&&(dep[e[i].ver]==0)) //分层 dep[e[i].ver]=dep[u]+1,q.push(e[i].ver); } if(dep[t]!=0) return 1; else return 0; //此时不存在分层图也不存在增广路 } int dfs(int u,int lastt){ int cnt=0; if(u==t) return lastt; //lastt:此点还剩余的流量 for(int i=cur[u];i&&cnt<lastt;i=e[i].nextt){ cur[u]=i; //当前弧优化 if((dep[e[i].ver]==dep[u]+1)&&(e[i].w!=0)){ int f=dfs(e[i].ver,min(lastt-cnt,e[i].w)); if(f>0){ e[i].w-=f,e[i^1].w+=f; cnt+=f; } } } if(cnt<lastt) dep[u]=-1; return cnt; } void dinic(){ ans=0; while(bfs()) ans+=dfs(s,inf); } char ss[519]; int a,b; //高走到低花费a;高换成低花费b #define pos(i,j) (i-1)*m+j //pos函数 int main(){ reads(n),reads(m),reads(a),reads(b); s=0,t=n*m+1; for(int i=1;i<=n;i++){ scanf("%s",ss+1); for(int j=1;j<=m;j++) { if(ss[j]=='#') add(s,pos(i,j),b); else add(pos(i,j),t,b); /*高低地分别向s、t连边*/ } } for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){ if(i>1) add(pos(i,j),pos(i-1,j),a); if(i<n) add(pos(i,j),pos(i+1,j),a); if(j>1) add(pos(i,j),pos(i,j-1),a); //相邻点 if(j<m) add(pos(i,j),pos(i,j+1),a); } dinic(); cout<<ans<<endl; return 0; //min_cut }

#include <cmath> #include <iostream> #include <cstdio> #include <string> #include <cstring> #include <vector> #include <algorithm> #include <queue> #include <stack> using namespace std; typedef long long ll; typedef unsigned long long ull; #define R register /*【p4126】最小割 // 最小割 + tarjan 对每条边询问:(1)是否存在割断该边的s-t最小割 (2)是否所有s-t最小割都割断该边。 */ /*【分析】(貌似是某结论题?)跑网络流最小割,然后在残量网络上跑Tarjan,缩点。 对于一条边满流的边x->y: 1. 如果x与y所属的SCC不同,则该边可能出现在最小割上; 2. 如果x与s所属的SCC相同且y与t所属的SCC相同,则该边一定出现在最小割上。*/ void reads(int &x){ //读入优化(正负整数) int f=1;x=0;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} x*=f; //正负号 } const int N=150019,inf=(int)2e9; int id[N*4]; int s,t,tot=1,n,m,ans[N],head[N],dep[N],cur[N]; //s为源点,t为汇点 struct node{ int nextt,ver; ll w; }e[N*4]; void add(int x,int y,int z,int i) { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,id[tot]=i,head[x]=tot; e[++tot].ver=x,e[tot].nextt=head[y],e[tot].w=0,id[tot]=0,head[y]=tot; } bool bfs(){ memset(dep,0,sizeof(dep)); //dep记录深度 memcpy(cur,head,sizeof(head)); queue<int> q; while(!q.empty()) q.pop(); dep[s]=1; q.push(s); while(!q.empty()){ int u=q.front(); q.pop(); for(int i=head[u];i;i=e[i].nextt) if((e[i].w>0)&&(dep[e[i].ver]==0)) //分层 dep[e[i].ver]=dep[u]+1,q.push(e[i].ver); } if(dep[t]!=0) return 1; else return 0; //此时不存在分层图也不存在增广路 } int dfs(int u,ll lastt){ int cnt=0; if(u==t) return lastt; //lastt:此点还剩余的流量 for(int i=cur[u];i&&cnt<lastt;i=e[i].nextt){ cur[u]=i; //当前弧优化 if((dep[e[i].ver]==dep[u]+1)&&(e[i].w!=0)){ int f=dfs(e[i].ver,min(lastt-cnt,e[i].w)); if(f>0){ e[i].w-=f,e[i^1].w+=f; cnt+=f; } } } if(cnt<lastt) dep[u]=-1; return cnt; } void dinic(){ while(bfs()) dfs(s,inf); } //不用计算min_cut int dfn[N],low[N],sta[N],vis[N],dfn_=0,top_=0,sum=0,col[N]; void tarjan(int u){ //dfn_记录当前dfs序到达的数字 dfn[u]=low[u]=++dfn_,vis[u]=1,sta[++top_]=u; //步骤一:初始化 for(int i=head[u];i;i=e[i].nextt){ //步骤二:枚举连向点,递归更新 if(!dfn[e[i].ver]) tarjan(e[i].ver),low[u]=min(low[u],low[e[i].ver]); else if(vis[e[i].ver]) low[u]=min(low[u],dfn[e[i].ver]); //这里写dfn或low都可以 } //↑↑步骤三:已经到达过,判断是否在当前栈内(栈内都是当前情况下能相连的点) if(dfn[u]==low[u]){ col[u]=++sum; vis[u]=0; while(sta[top_]!=u){ //u上方的节点是可以保留的 col[sta[top_]]=sum; vis[sta[top_]]=0,top_--; } top_--; //col数组记录每个点所在连通块的编号 } } int main(){ reads(n),reads(m),reads(s),reads(t); ll z; for(int i=1,x,y;i<=m;i++) reads(x),reads(y), scanf("%lld",&z),add(x,y,z,i); dinic(); for(int i=1;i<=n;i++) if(!vis[i]) tarjan(i); for(int x=1;x<=n;x++) for(int i=head[x];i;i=e[i].nextt) if(id[i]&&!e[i].w) ans[id[i]]=(col[x]!=col[e[i].ver]) +((col[x]==col[s]&&col[e[i].ver]==col[t])<<1); for(int i=1;i<=m;i++) printf("%d %d\n",ans[i]&1,ans[i]>>1); //yes no }
【p4126】最小割 // 最小割 + tarjan
对每条边询问: (1)是否存在割断该边的s-t最小割。
(2)是否所有s-t最小割都割断该边。
思路:跑网络流最小割,然后在残量网络上跑Tarjan,缩点。
结论:对于 一条满流的边x->y 1. 如果x与y所属的SCC不同,则该边可能出现在最小割上;
2. 如果x与s所属的SCC相同且y与t所属的SCC相同,则该边一定出现在最小割上。
其他网络流相关解读:https://blog.csdn.net/qq_41357771/article/details/79416899
——时间划过风的轨迹,那个少年,还在等你



