【暖*墟】#洛谷网课1.30# 树上问题
树上倍增
基环外向树DP
DFS序与欧拉序
树链剖分
可以参考wjyyy的https://www.wjyyy.top/421.html
wjyyy是这样说的：
树链剖分是一种优化，将树上最常经过的几条链划为重点，用线段树来优化区间修改和查询。
并且因为在一棵子树中dfs序是连续的，并且在任意一条重链上，dfs序也是连续的，
可以认为轻链是单点修改，重链是区间修改，轻重分明，时间复杂度O(Nlog2N)。
【概念简述】
即如图所示： 
即： 
【原理分析】
10->3可以拆成 10->8的重链 + 8->1的轻边 + 1->3的重链
（1）信息记录在点上，在线段树上直接修改[1,3],[8,10]；
（2）信息记录在边上，在线段树上，用点标识父边，即：[2,3],[9,10],单点8 的修改。
【具体操作】
记录 top 信息：如图，1、2、3、4、5的 top 是1；8、9、10的 top 是8；其他的 top 都是自己。
确定一条链的重链轻边：1.选 top 大的点向上跳；
2.每次跳到重链顶端或一条轻边；3.直到两个点在同一重链上。
根据两遍dfs得到的信息 --> 初始化线段树。
（1）第一次dfs，求子树大小size[ ]，深度dep[ ]，重儿子son[ ]。
（2）第二次 dfs，id[x] 记录树链剖分之后的 dfs 序。
若有重儿子，优先 dfs 传递到底；若是轻边，每个轻边的子节点的 top 都是自己。
目的：求出 top（划分轻重链）、确定 dfs 序。
（3）query 函数：查询区间（链）信息。
深度大的节点向上跳，每次跳某个轻边或者跳完整个重链。
其中信息经过 get 函数的线段树方式处理，可以实现区间维护。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<string> #include<queue> #include<vector> #include<cmath> #include<map> using namespace std; typedef long long ll; //【p2590】树的统计 void reads(int &x){ //读入优化（正负整数） int fa=1;x=0;char s=getchar(); while(s<'0'||s>'9'){if(s=='-')fa=-1;s=getchar();} while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+s-'0';s=getchar();} x*=fa; //正负号 } const int N=60019,M=200019; int n,m,a[N],sumn,maxn,tot=0,head[N]; int siz[N],son[N],top[N],dep[N],fa[N]; int seg[N],rev[M],sum[M],Max[M]; struct node{ int nextt,ver,w; }e[N]; void add(int x,int y) { e[++tot].ver=y,e[tot].nextt=head[x],head[x]=tot; } //--------线段树部分----------\\ void build(int rt,int l,int r){ int mid=(l+r)>>1; if(l==r){ Max[rt]=sum[rt]=a[rev[l]]; return; } //叶子节点 build(rt<<1,l,mid),build((rt<<1)+1,mid+1,r); //左右子树 sum[rt]=sum[rt<<1]+sum[(rt<<1)+1];//更新相关值 Max[rt]=max(Max[rt<<1],Max[(rt<<1)+1]); } void change(int rt,int l,int r,int v,int x){ //单点修改 if((x>r)||(x<l)) return; //x超出范围 if((l==r)&&(r==x)){ //到达叶子节点x，开始修改 sum[rt]=v,Max[rt]=v; return; } int mid=(l+r)>>1; if(mid>=x) change(rt<<1,l,mid,v,x); //左儿子 if(mid+1<=x) change((rt<<1)+1,mid+1,r,v,x); //右儿子 sum[rt]=sum[rt<<1]+sum[(rt<<1)+1];//更新相关的值 Max[rt]=max(Max[rt<<1],Max[(rt<<1)+1]); } void get(int rt,int l,int r,int x,int y){ //区间询问，rt是节点标号，l、r是当前区间，x、y是询问区间 if((x>r)||(y<l)) return; //与询问区间无交集 if((x<=l)&&(r<=y)) //询问区间包含于当前区间 { sumn+=sum[rt],maxn=max(maxn,Max[rt]); return; } int mid=(l+r)>>1; if(mid>=x) get(rt<<1,l,mid,x,y); //左儿子 if(mid+1<=y) get((rt<<1)+1,mid+1,r,x,y); //右儿子 } //--------树链剖分部分----------\\ void dfs1(int u,int fa_){ //第一遍dfs：求子树大小和重儿子 siz[u]=1,fa[u]=fa_,dep[u]=dep[fa_]+1; for(int i=head[u];i;i=e[i].nextt){ if(e[i].ver==fa_) continue; dfs1(e[i].ver,u),siz[u]+=siz[e[i].ver]; //计算size if(siz[e[i].ver]>siz[son[u]]) son[u]=e[i].ver; //重儿子 } } void dfs2(int u,int fa_){ //第二遍dfs：确定dfs序和top值 if(son[u]){ //先走重儿子，使重链在线段树中的位置连续 seg[son[u]]=++seg[0]; //节点记入线段树中 rev[seg[0]]=son[u]; //记录对应的原始编号 top[son[u]]=top[u],dfs2(son[u],u); //更新top值 } for(int i=head[u];i;i=e[i].nextt){ if(top[e[i].ver]) continue; //除去u的重儿子或父亲 seg[e[i].ver]=++seg[0],rev[seg[0]]=e[i].ver; //加入线段树 top[e[i].ver]=e[i].ver,dfs2(e[i].ver,u); //轻边上的点 } } void query(int x,int y){ //路径询问 int fx=top[x],fy=top[y]; while(fx!=fy){ //↓↓选择深度较大的 if(dep[fx]<dep[fy]) swap(x,y),swap(fx,fy); get(1,1,seg[0],seg[fx],seg[x]); x=fa[fx],fx=top[x]; //往上跳、并更新此点的top值 } if(dep[x]>dep[y]) swap(x,y); //x、y已在同一条重链上 get(1,1,seg[0],seg[x],seg[y]); } //--------主程序部分----------\\ int main(){ int u,v; reads(n); for(int i=1;i<n;i++) reads(u),reads(v),add(u,v),add(v,u); for(int i=1;i<=n;i++) reads(a[i]); dfs1(1,0),seg[0]=seg[1]=top[1]=rev[1]=1; //设1为根结点 dfs2(1,0),build(1,1,seg[0]); //建立线段树 reads(m); char ss[10]; for(int i=1;i<=m;i++){ scanf("%s",ss+1); reads(u),reads(v); if(ss[1]=='C') change(1,1,seg[0],v,seg[u]); //单点修改 else{ sumn=0,maxn=-10000000,query(u,v); //询问 if(ss[2]=='M') printf("%d\n",maxn); else printf("%d\n",sumn); } } }
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<string> #include<queue> #include<vector> #include<cmath> #include<map> using namespace std; typedef long long ll; /*【p3178】树上操作 有一棵点数为 N 的树，以点1为根，且有边权。M 个操作： 1：把某个节点 x 的点权增加 a（单点修改） 2：把某个节点 x 为根的子树中所有点的点权都增加 a（区间修改） 3：询问某个节点 x 到根的路径中所有点的点权和（区间查询） */ void reads(ll &x){ //读入优化（正负整数） ll fa=1;x=0;char s=getchar(); while(s<'0'||s>'9'){if(s=='-')fa=-1;s=getchar();} while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+s-'0';s=getchar();} x*=fa; //正负号 } const ll N=1000019; ll n,m,a[N*2],tot=0,head[N*2]; ll siz[N*2],son[N*2],top[N*2],dep[N*2],fa[N*2]; ll rev[N*2],seg[N*4],sum[N*4],lazy[N*4]; struct node{ ll nextt,ver,w; }e[N*2]; void add(ll x,ll y) { e[++tot].ver=y,e[tot].nextt=head[x],head[x]=tot; } //--------线段树部分----------// void build(ll rt,ll l,ll r){ ll mid=(l+r)>>1; if(l==r){ sum[rt]=a[rev[l]]; return; } //叶子节点 build(rt<<1,l,mid),build(rt<<1|1,mid+1,r); //左右子树 sum[rt]=sum[rt<<1]+sum[rt<<1|1]; } void PushDown(ll rt,ll l,ll r){ //标记下移 if(!lazy[rt]) return; ll mid=(l+r)>>1; sum[rt<<1]+=lazy[rt]*(mid-l+1); sum[rt<<1|1]+=lazy[rt]*(r-mid); lazy[rt<<1]+=lazy[rt],lazy[rt<<1|1]+=lazy[rt]; lazy[rt]=0; //此点标记清零 } void change(ll rt,ll l,ll r,ll v,ll x,ll y){ //区间修改 if((x>r)||(y<l)) return; //不相交区间 if((x<=l)&&(r<=y)) //此区间完全被询问区间包含 { sum[rt]+=v*(r-l+1),lazy[rt]+=v; return; } ll mid=(l+r)>>1; PushDown(rt,l,r); change(rt<<1,l,mid,v,x,y),change(rt<<1|1,mid+1,r,v,x,y); sum[rt]=sum[rt<<1]+sum[rt<<1|1]; } ll get(ll rt,ll l,ll r,ll x,ll y){ //区间询问，rt是节点标号，l、r是当前区间，x、y是询问区间 if((x>r)||(y<l)) return 0; //与询问区间无交集 if((x<=l)&&(r<=y)) return sum[rt]; ll mid=(l+r)>>1; PushDown(rt,l,r); return get(rt<<1,l,mid,x,y)+get(rt<<1|1,mid+1,r,x,y); } //--------树链剖分部分----------// void dfs1(ll u,ll fa_){ //第一遍dfs：求子树大小和重儿子 siz[u]=1,fa[u]=fa_,dep[u]=dep[fa_]+1; for(ll i=head[u];i;i=e[i].nextt){ if(e[i].ver==fa_) continue; dfs1(e[i].ver,u),siz[u]+=siz[e[i].ver]; //计算size if(siz[e[i].ver]>siz[son[u]]) son[u]=e[i].ver; //重儿子 } } void dfs2(ll u,ll fa_){ //第二遍dfs：确定dfs序和top值 if(son[u]){ //先走重儿子，使重链在线段树中的位置连续 seg[son[u]]=++seg[0]; //节点记入线段树中 rev[seg[0]]=son[u]; //记录对应的原始编号 top[son[u]]=top[u],dfs2(son[u],u); //更新top值 } for(ll i=head[u];i;i=e[i].nextt){ if(top[e[i].ver]) continue; //除去u的重儿子或父亲 seg[e[i].ver]=++seg[0],rev[seg[0]]=e[i].ver; //加入线段树 top[e[i].ver]=e[i].ver,dfs2(e[i].ver,u); //轻边上的点 } } ll query(ll x,ll y){ //路径询问 ll fx=top[x],fy=top[y],ans=0; while(fx!=fy){ //↓↓选择深度较大的 if(dep[fx]<dep[fy]) swap(x,y),swap(fx,fy); ans=ans+get(1,1,seg[0],seg[fx],seg[x]); x=fa[fx],fx=top[x]; //往上跳、并更新此点的top值 } if(dep[x]>dep[y]) swap(x,y); //x、y已在同一条重链上 ans=ans+get(1,1,seg[0],seg[x],seg[y]); return ans; } //--------主程序部分----------// int main(){ //freopen("1.in","r",stdin); ll u,v,op; reads(n),reads(m); for(ll i=1;i<=n;i++) reads(a[i]); for(ll i=1;i<n;i++) reads(u),reads(v),add(u,v),add(v,u); dfs1(1,0),seg[0]=seg[1]=top[1]=rev[1]=1; //设1为根结点 dfs2(1,0),build(1,1,seg[0]); //建立线段树 for(ll i=1;i<=m;i++){ reads(op),reads(u); if(op==1) reads(v),change(1,1,seg[0],v,seg[u],seg[u]); if(op==2) reads(v),change(1,1,n,v,seg[u],seg[u]+siz[u]-1); if(op==3) printf("%lld\n",query(1,u)); } }
边权的树链剖分：P1505 [国家集训队]旅游
树分治
统计树中各种链的信息：点分治，边分治，链分治。
点分治及相关应用
#include<cmath> #include<cstdio> #include<cstring> #include<cassert> #include<iostream> #include<algorithm> #include<queue> #include<vector> #include<map> #include<set> #include<deque> using namespace std; typedef long long ll; /*【p2634】聪聪可可 树上路径长度是3的倍数的概率。 */ //【分析】考虑经过一个点的路径，num[i]表示距离%3==i的点的个数。 //那么长度是3的倍数路径总数为num[0]*num[0]+num[1]*num[2]*2。 //用点分治的【容斥原理】思想，逐步划分求解。 void reads(int &x){ //读入优化（正负整数） ll f=1;x=0;char s=getchar(); while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();} while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();} x*=f; //正负号 } const int N=50019; struct edge{ int ver,nextt,w; }e[N<<1]; //边集 int n,m,k,head[N],cnt; //head[]和cnt是边集数组的辅助变量 int root,sum; //当前查询的根，当前递归的这棵树的大小 int vis[N]; //某一个点是否被当做根过 int sz[N]; //每个点下面子树的大小 int f[N]; //每个点为根时，最大子树大小 int dep[N],num[N]; //dep是每个点的深度(与当前根节点的距离) int ans; //最终统计的答案 void getroot(int u,int fa){ //dfs求重心和子树大小 sz[u]=1; f[u]=0; for(int i=head[u];i;i=e[i].nextt){ int v=e[i].ver; if(v==fa||vis[v]) continue; getroot(v,u); sz[u]+=sz[v]; f[u]=max(f[u],sz[v]); } f[u]=max(f[u],sum-sz[u]); //注意：可能是另外一半的树 if(f[u]<f[root]) root=u; //更新重心 } void getdeep(int u,int fa){ //dfs求出与根节点的距离 num[dep[u]]++; //对于当前根节点，求距离%3==i的点的个数 for(int i=head[u];i;i=e[i].nextt){ int v=e[i].ver; if(v==fa||vis[v]) continue; dep[v]=(dep[u]+e[i].w)%3; getdeep(v,u); } } int calc(int u,int lastt){ //lastt可能是0或e[i].w dep[u]=lastt%3; memset(num,0,sizeof(num)); getdeep(u,0); return num[0]*num[0]+num[1]*num[2]*2; } void solve(int u){ ans+=calc(u,0); vis[u]=1; //↑↑会产生非法路径（被u的某个子树完全包含，路径不能合并） for(int i=head[u];i;i=e[i].nextt){ //递归子树 int v=e[i].ver; if(vis[v]) continue; ans-=calc(v,e[i].w); //容斥原理去除非法答案 //↑↑在处理子树时，将初始长度设为连接边长e[i].w; //这样做就相当于给子树的每个组合都加上了u—>的路径。 sum=sz[v]; root=0; //重设当前总树大小，寻找新的分治点 getroot(v,0); solve(root); //递归新的分治点（重心） } } int gcd(int a,int b){ return (b==0)?a:gcd(b,a%b); } int main(){ reads(n); int u,v,w; for(int i=1;i<n;i++){ reads(u),reads(v),reads(w); //↓前向星 e[++cnt]=(edge){v,head[u],w}; head[u]=cnt; e[++cnt]=(edge){u,head[v],w}; head[v]=cnt; } sum=f[0]=n; root=0; getroot(1,0); solve(root); int gcds=gcd(ans,n*n); //路径总条数为n*n printf("%d/%d\n",ans/gcds,n*n/gcds); return 0; }
边分治及其应用
（1）找中心边 -> 处理经过它的路径 -> 删掉中心边。
（2）优化【防被菊花树卡掉】：加点重构，把树变成二叉树。
这样，边分治就只用考虑两棵子树，其他操作与点分治类似。
-----> 
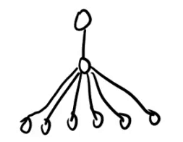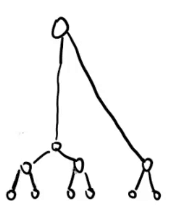
即：用类似于安排管理节点的方法，加点重构。
链分治及其应用
即：对于树链剖分的结构进行分治。
