【暖*墟】#洛谷网课1.29# 图与网络流

 二分图匹配

 

 二分图相关结论

 

 

 匈牙利算法

int linker[MAXN * 2]; //右侧点的左侧匹配点

bool used[MAXN * 2]; //用于dfs标记访问

bool dfs(int u) {
    for (int i = head[u]; i; i = e[i].nextt) {
        int v = e[i].ver;
        if (!used[v]) { used[v] = true;
            if (linker[v] == -1 || dfs(linker[v])) 
             {  linker[v] = u; return true; } }
    } return false;
}

int hungarian(int n) {
    int res = 0; for (int i = 0; i <= n * 2; i++) linker[i] = -1;
    for (int u = 1; u <= n; u++) { //每次新加一点、判断是否有增广路
        for (int i = 1; i <= n * 2; i++) used[i] = 0;
        if (dfs(u)) res++; //↑↑需要多次清空used数组
    }  return res; //二分图最大匹配
}         

 

 KM算法的扩展

 

 网络流模型

有向图；源点S，汇点T；边流量<=容量；反对称性；流守恒 --> 流量最大的可行流

 

 网络流建图

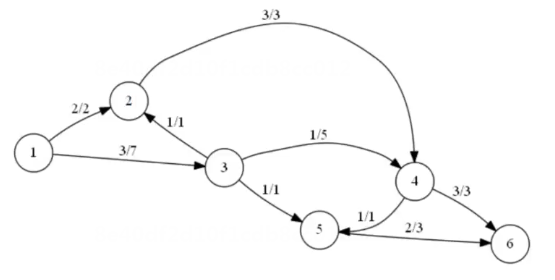
【反向边】此边上已经走过的流量；【正向边】不断减小，表示还能走过的流量 -> 构成残量网络。

【增广路】残量网络中，若存在一条s->t的路径，且每条边权值>0，

                说明可以通过这条路径增加原网络的流量。

• 经过反向边的增广路相当于减小原来那条边的容量，便于增广路的判断。

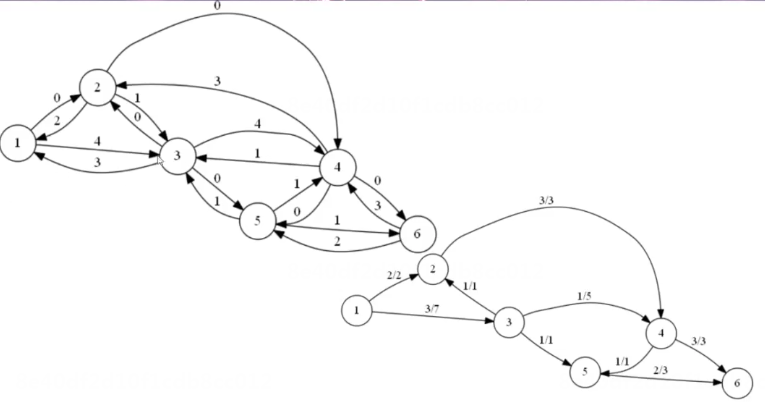
把边权（容量）为0的边隐藏起来（可以不用考虑），得到：

 

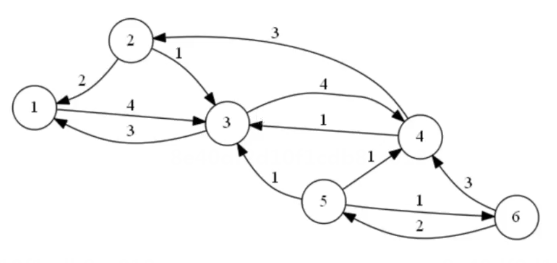
 Edmonds-Karp算法

 缺点：时间慢；优点：可以处理带权流的问题。

 

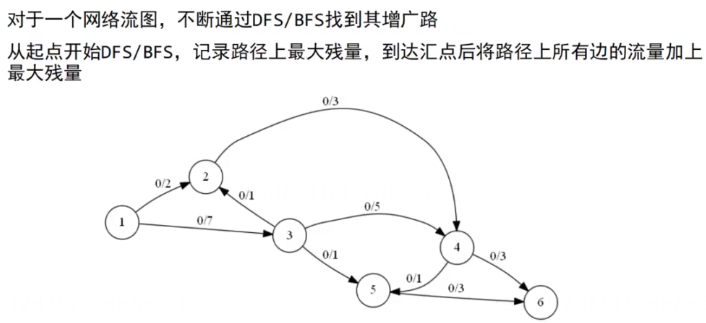
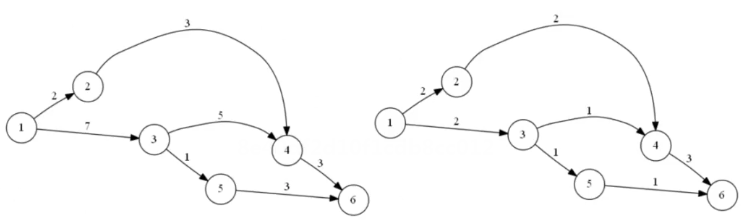
 Dinic算法

bfs将图分层，dfs寻找“阻塞”（增广路）。

struct Edge {
    int from, to,rev;
    int cap, flow; //容量，流量
    Edge(){}
    Edge(int _from, int _to, int _cap, int _flow, int _rev):
       from(_from), to(_to), cap(_cap), flow(_flow), rev(_rev) {};
}; vector<Edge> g[MAXN];

int cur[MAXN]; //当前点已经处理完了一部分下层点，从后方继续

inline void insert(int u, int v, int c) {
    g[u].push_back(Edge(u, v, c, 0, g[v].size()));
    g[v].push_back(Edge(v, u, 0, 0, g[u].size()-1));
}

int d[MAXN],q[MAXN], qhead, qtail;

int bfs() { //用bfs实现“分层”
    memset(d, 0, sizeof(d)); //dep
    qhead = qtail = 0, q[qtail++] = s, d[s] = 1;
    while (qhead != qtail) {
        int now = q[qhead++];
        for (auto e : g[now]) 
            if (!d[e.to] && e.cap > e.flow) 
               d[e.to] = d[now] + 1, q[qtail++] = e.to;
    } return d[t];
}

int dfs(int now, int a) { //a：此点剩余流量
    if (now == t || !a) return a; int flow = 0;
    for (int &i = cur[now]; i < g[now].size(); i++) {
        Edge &e = g[now][i]; //↑↑ &i=cur[now] 即：从上次停下来的地方继续
        if (d[e.to] == d[now] + 1 && e.cap > e.flow) { //有增广路到达下层
            int f = dfs(e.to, min(a, e.cap - e.flow)); 
           //↑↑ dfs（下个点流量，min（此点剩余流量，此边剩余流量））;
            a -= f, flow += f, e.flow += f, g[e.to][e.rev].flow -= f;
        } if (!a) break;
    } if (a) d[now] = -1; return flow; //把多余流量放到全部的最前面，防止出现干扰
}

int dinic() {
    int flow = 0;
    while (bfs()) {
        memset(cur, 0, sizeof(cur));
        flow += dfs(s, INF);
    } return flow;
}

 

 最大流模型

 

相关练习题

 

#include <cmath>
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <vector>
#include <algorithm>
#include <queue>
#include <stack>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;

#define R register

//【最大流】dinic：bfs求分层图 + dfs求增广路

//1.根据从源点开始的bfs序列，为每一个点分配一个深度；（不会向回流）
//2.进行若干遍dfs寻找增广路，每一次由u推出v必须保证v的深度必须是u的深度+1。

void reads(int &x){ //读入优化（正负整数）
    int f=1;x=0;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    x*=f; //正负号
}

const int N=1000019,INF=99999999;

int s,t,tot=-1,n,m,head[N],dep[N]; //s为源点，t为汇点 

struct node{ int nextt,ver,w; }e[N];

void add(int x,int y,int z)
 { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,head[x]=tot; }

int bfs(){
    memset(dep,0,sizeof(dep)); //dep记录深度 
    queue<int> q; while(!q.empty()) q.pop();
    dep[s]=1; q.push(s);
    while(!q.empty()){
        int u=q.front(); q.pop();
        for(int i=head[u];i!=-1;i=e[i].nextt)
            if((e[i].w>0)&&(dep[e[i].ver]==0)) //分层 
                dep[e[i].ver]=dep[u]+1,q.push(e[i].ver);
    } if(dep[t]!=0) return 1;
      else return 0; //此时不存在分层图也不存在增广路
}

int dfs(int u,int lastt){
    if(u==t) return lastt; //lastt：此点还剩余的流量
    for(int i=head[u];i!=-1;i=e[i].nextt) 
        if((dep[e[i].ver]==dep[u]+1)&&(e[i].w!=0)){
            int f=dfs(e[i].ver,min(lastt,e[i].w)); 
            if(f>0){ e[i].w-=f,e[i^1].w+=f; return f; }
    } return 0; //没有dfs>0即说明没有增广路，返回0
}

int dinic(){ int ans=0; while(bfs()) ans+=dfs(s,INF); return ans; }

int main(){
    reads(n),reads(m),reads(s),reads(t);
    int x,y,z; memset(head,-1,sizeof(head));
    for(int i=1;i<=m;i++){
        reads(x),reads(y),reads(z),
        add(x,y,z),add(y,x,0); //反边初始流量为0
    } cout<<dinic()<<endl; return 0;
}

 

#include <cmath>
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <vector>
#include <algorithm>
#include <queue>
#include <stack>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;

#define R register

/*【p2740】草地排水 */

//【标签】网络流、最大流Dinic算法

void reads(int &x){ //读入优化（正负整数）
    int f=1;x=0;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    x*=f; //正负号
}

const int N=1000019,INF=99999999;

int s,t,tot=-1,n,m,head[N],dep[N]; //s为源点，t为汇点 

struct node{ int nextt,ver,w; }e[N];

void add(int x,int y,int z)
 { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,head[x]=tot; }

int bfs(){
    memset(dep,0,sizeof(dep)); //dep记录深度 
    queue<int> q; while(!q.empty()) q.pop();
    dep[s]=1; q.push(s);
    while(!q.empty()){
        int u=q.front(); q.pop();
        for(int i=head[u];i!=-1;i=e[i].nextt)
            if((e[i].w>0)&&(dep[e[i].ver]==0)) //分层 
                dep[e[i].ver]=dep[u]+1,q.push(e[i].ver);
    } if(dep[t]!=0) return 1;
      else return 0; //此时不存在分层图也不存在增广路
}

int dfs(int u,int lastt){
    if(u==t) return lastt; //lastt：此点还剩余的流量
    for(int i=head[u];i!=-1;i=e[i].nextt) 
        if((dep[e[i].ver]==dep[u]+1)&&(e[i].w!=0)){
            int f=dfs(e[i].ver,min(lastt,e[i].w)); 
            if(f>0){ e[i].w-=f,e[i^1].w+=f; return f; }
    } return 0; //没有dfs>0即说明没有增广路，返回0
}

int dinic(){ int ans=0; while(bfs()) ans+=dfs(s,INF); return ans; }

int main(){
    reads(m),reads(n),s=1,t=n;
    int x,y,z; memset(head,-1,sizeof(head));
    for(int i=1;i<=m;i++){
        reads(x),reads(y),reads(z),
        add(x,y,z),add(y,x,0); //反边初始流量为0
    } cout<<dinic()<<endl; return 0;
}

 

#include <cmath>
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <vector>
#include <algorithm>
#include <queue>
#include <stack>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;

#define R register

//【p1231】教辅的组成
//给出 书和练习册、书和答案 的对应关系，求同时配成的 书-练习册-答案 的组数。*/

//【分析】源点->练习册->书(拆点)->答案->汇点
//相关编号顺序可以看 https://cdn.luogu.org/upload/pic/13675.png

// Q:为什么书要拆点？ A:每本书只能用一次，如果只有一个点，左右可能有多条路径、不唯一。

//1.根据从源点开始的bfs序列，为每一个点分配一个深度；（不会向回流）
//2.进行若干遍dfs寻找增广路，每一次由u推出v必须保证v的深度必须是u的深度+1。

void reads(int &x){ //读入优化（正负整数）
    int f=1;x=0;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    x*=f; //正负号
}

const int N=1000019;

int s,t,tot=-1,n1,n2,n3,head[N],dep[N]; //s为源点，t为汇点 

struct node{ int nextt,ver,w; }e[N];

void add(int x,int y,int z) //正向边权值为1，反向边权值为0
 { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,head[x]=tot;
   e[++tot].ver=x,e[tot].nextt=head[y],e[tot].w=0,head[y]=tot; }

int bfs(){
    memset(dep,0,sizeof(dep)); //dep记录深度 
    queue<int> q; while(!q.empty()) q.pop();
    dep[s]=1; q.push(s); 
    while(!q.empty()){
        int u=q.front(); q.pop();
        for(int i=head[u];i!=-1;i=e[i].nextt)
            if((e[i].w>0)&&(dep[e[i].ver]==0)) //分层 
                dep[e[i].ver]=dep[u]+1,q.push(e[i].ver);
    } if(dep[t]!=0) return 1;
      else return 0; //此时不存在分层图也不存在增广路
}

int dfs(int u,int lastt){ int ans=0; 
    if(u==t) return lastt; //lastt：此点还剩余的流量
    for(int i=head[u];i!=-1&&ans<lastt;i=e[i].nextt) 
        if((dep[e[i].ver]==dep[u]+1)&&(e[i].w!=0)){
            int f=dfs(e[i].ver,min(lastt-ans,e[i].w)); 
            if(f>0){ e[i].w-=f,e[i^1].w+=f,ans+=f; }
    } if(ans<lastt) dep[u]=-1; return ans;
}

int dinic(){ int ans=0; while(bfs()) ans+=dfs(s,1<<30); return ans; }

int id(int typ,int x){ if(typ==1) return x; if(typ==2) return n2+x;
   if(typ==3) return n2+n1+x; if(typ==4) return n2+n1+n1+x; }

int main(){ memset(head,-1,sizeof(head));
    int m,u,v; reads(n1),reads(n2),reads(n3); //三种物品的数目
    //种类： 1.练习册; 2.书拆点1; 3.书拆点2; 4.答案。
    reads(m); while(m--) reads(u),reads(v),add(id(1,v),id(2,u),1);
    reads(m); while(m--) reads(u),reads(v),add(id(3,u),id(4,v),1);
    for(int i=1;i<=n1;i++) add(id(2,i),id(3,i),1); //书拆点的连边
    s=0,t=n2+n1+n1+n3+1; for(int i=1;i<=n2;i++) add(s,id(1,i),1);
    for(int i=1;i<=n3;i++) add(id(4,i),t,1); //起点&终点的连边
    printf("%d\n",dinic()); return 0; //每条路径权值是1，最大流就是组数
}

 

#include <cmath>
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <vector>
#include <algorithm>
#include <queue>
#include <stack>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;

#define R register

//【p2936】全流 dinic模板

//1.根据从源点开始的bfs序列，为每一个点分配一个深度；（不会向回流）
//2.进行若干遍dfs寻找增广路，每一次由u推出v必须保证v的深度必须是u的深度+1。

void reads(int &x){ //读入优化（正负整数）
    int f=1;x=0;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    x*=f; //正负号
}

const int N=1000019;

int s,t,tot=-1,n,head[N],dep[N]; //s为源点，t为汇点 

struct node{ int nextt,ver,w; }e[N];

void add(int x,int y,int z) //正向边权值为1，反向边权值为0
 { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,head[x]=tot; }

int bfs(){
    memset(dep,0,sizeof(dep)); //dep记录深度 
    queue<int> q; while(!q.empty()) q.pop();
    dep[s]=1; q.push(s); 
    while(!q.empty()){
        int u=q.front(); q.pop();
        for(int i=head[u];i!=-1;i=e[i].nextt)
            if((e[i].w>0)&&(dep[e[i].ver]==0)) //分层 
                dep[e[i].ver]=dep[u]+1,q.push(e[i].ver);
    } if(dep[t]!=0) return 1;
      else return 0; //此时不存在分层图也不存在增广路
}

int dfs(int u,int lastt){ int ans=0; 
    if(u==t) return lastt; //lastt：此点还剩余的流量
    for(int i=head[u];i!=-1&&ans<lastt;i=e[i].nextt) 
        if((dep[e[i].ver]==dep[u]+1)&&(e[i].w!=0)){
            int f=dfs(e[i].ver,min(lastt-ans,e[i].w)); 
            if(f>0){ e[i].w-=f,e[i^1].w+=f,ans+=f; }
    } if(ans<lastt) dep[u]=-1; return ans;
}

int dinic(){ int ans=0; while(bfs()) ans+=dfs(s,1<<30); return ans; }

int main(){ 
    memset(head,-1,sizeof(head));
    reads(n); string a,b; s=1,t=26;
    for(int i=1,x,y,z;i<=n;i++){
        cin>>a>>b>>z; x=a[0]-'A'+1,y=b[0]-'A'+1;
        add(x,y,z),add(y,x,0); //正反边
    } cout<<dinic()<<endl; return 0;
}

 

最小路径覆盖问题

• 反链：一个点集，任意两个元素都不在同一条链上。
• 覆盖：所有点都能分布在链上，需要的最小链数。
• 最小路径覆盖：有向无环图中，用最少多少条简单路径能将所有的点覆盖。
• 简单路径：就是一条路径不能和其他路径有重复的点，当然也可以认为单个点是一条简单路径）。

根据二分图性质，【最小链覆盖数 = 最长反链长度】【最长链长度 = 最小反链覆盖数】。

 

（1）二分图匹配算法 //求最大匹配 + 输出匹配方案

• 【二分图求最小链覆盖数】相当于把每个点拆成两个点，求最大点独立集的大小。
• 当两边点数相同时（完美匹配），最大点独立集大小=左边点数n-最大匹配数。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<cmath>
#include<map>
#include<set>
using namespace std;
typedef long long ll;

/*【p2764】最小路径覆盖问题 */

const int N=159;

struct edge{ int ver,nextt; }e[N*N];

int n,m,head[N],tot=0,vis[N],match[N];

void add(int x,int y){ e[++tot].ver=y,e[tot].nextt=head[x],head[x]=tot; }

bool dfs1(int x){ //二分图匹配
    for(int i=head[x];i;i=e[i].nextt){
        if(!vis[e[i].ver]){ vis[e[i].ver]=1;
            if(!match[e[i].ver]||dfs1(match[e[i].ver])){
                match[e[i].ver]=x; return true;
            }
        }
    } return false;
}

void dfs2(int now){ //最小链覆盖的方案
    if(!match[now]){ printf("%d ",now); return; }
    dfs2(match[now]); printf("%d ",now); //↓↓即最小链覆盖的方案
} //相当于将一开始分开的两个点合并起来，按照匹配路径，寻找每条链的链长

int main(){
    int x,y,ans=0; scanf("%d%d",&n,&m);
    
    for(int i=1;i<=m;i++)
        scanf("%d%d",&x,&y),add(x,y);
    for(int i=1;i<=n;i++){
        memset(vis,0,sizeof(vis));
        if(dfs1(i)) ans++;
    } //↑↑求二分图最大匹配数
    
    memset(vis,0,sizeof(vis));
    for(int i=1;i<=n;i++) vis[match[i]]=1; 
    //↑↑用vis数组来标记被右边的点匹配上了的左边点
    for(int i=1;i<=n;i++) //左边点中没有匹配上的就在点独立集中
        if(!vis[i]){ dfs2(i); printf("\n"); }
    
    printf("%d\n",n-ans); return 0;
}

 

（2）网络最大流算法 //求最小路径覆盖及方案

• 附加超级源点Ｓ和超级汇点Ｔ，建边权为1的图，ans从n开始倒着减，运行最大流。
• 输出方案，即：从汇点T按残余流量的有无，往前找每条路径，并递归输出。

 

注意dinic_函数的写法：

void dinic_(){ ans=n; while(bfs()) ans-=dfs(s,1<<30); }

 

注意求方案的递归函数的写法：

void print(int x){
    if(x<=s) return; //到达起点，输入完毕
    printf("%d ",x); //因为连的每条边都是从i->j+n
    for(int i=head[x];i!=-1;i=e[i].nextt) //所以递归的e[i].ver一定>n
       if(!e[i].w&&e[i].ver<=n*2) print(e[i].ver-n);
}

 

总代码实现（洛谷 P2764 最小路径覆盖问题）：

#include <cmath>
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <vector>
#include <algorithm>
#include <queue>
#include <stack>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;

#define R register

//【p2764】最小路径覆盖问题

//附加超级源点Ｓ和超级汇点Ｔ，建边权为1的图，运行最大流。

void reads(int &x){ //读入优化（正负整数）
    int f=1;x=0;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    x*=f; //正负号
}

const int N=1000019;

int s,t,tot=-1,n,m,ans,head[N],dep[N]; //s为源点，t为汇点 

struct node{ int nextt,ver,w; }e[N];

void add(int x,int y,int z) //正向边权值为1，反向边权值为0
 { e[++tot].ver=y,e[tot].nextt=head[x],e[tot].w=z,head[x]=tot; }

int bfs(){
    memset(dep,0,sizeof(dep)); //dep记录深度 
    queue<int> q; while(!q.empty()) q.pop();
    dep[s]=1; q.push(s); 
    while(!q.empty()){
        int u=q.front(); q.pop();
        for(int i=head[u];i!=-1;i=e[i].nextt)
            if((e[i].w>0)&&(dep[e[i].ver]==0)) //分层 
                dep[e[i].ver]=dep[u]+1,q.push(e[i].ver);
    } if(dep[t]!=0) return 1;
      else return 0; //此时不存在分层图也不存在增广路
}

int dfs(int u,int lastt){ int ans=0; 
    if(u==t) return lastt; //lastt：此点还剩余的流量
    for(int i=head[u];i!=-1&&ans<lastt;i=e[i].nextt) 
        if((dep[e[i].ver]==dep[u]+1)&&(e[i].w!=0)){
            int f=dfs(e[i].ver,min(lastt-ans,e[i].w)); 
            if(f>0){ e[i].w-=f,e[i^1].w+=f,ans+=f; }
    } if(ans<lastt) dep[u]=-1; return ans;
}

void print(int x){
    if(x<=s) return; //到达起点，输入完毕
    printf("%d ",x); //因为连的每条边都是从i->j+n
    for(int i=head[x];i!=-1;i=e[i].nextt) //所以递归的e[i].ver一定>n
       if(!e[i].w&&e[i].ver<=n*2) print(e[i].ver-n);
}

void dinic_(){ ans=n; while(bfs()) ans-=dfs(s,1<<30); }

int main(){ 
    memset(head,-1,sizeof(head));
    reads(n),reads(m); s=0,t=519;
    for(int i=1;i<=n;i++) //超级源点/汇点的连边
        add(s,i,1),add(i,s,0),add(i+n,t,1),add(t,i+n,0);
    for(int i=1,u,v;i<=m;i++) //拆点
        reads(u),reads(v),add(u,v+n,1),add(v+n,u,0);
    dinic_(); //↓↓从汇点按残余流量的有无，往前找一条路径，并递归输出
    for(int i=head[t];i!=-1;i=e[i].nextt){ //输出方案
        if(e[i].w) continue; //不选还有剩余的
        print(e[i].ver-n),printf("\n"); //递归输出
    } printf("%d\n",ans); return 0; //最小链覆盖
}

 

 

 费用流模型

在网络流图的模型上，每条边增加权值cost，某个可行流的 费用 = 流量 * cost 。

最小费用最大流（mcmf）：在满足流量最大的前提下，找出费用最小的方案。

#include <cmath>
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <vector>
#include <algorithm>
#include <queue>
#include <stack>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;

#define R register

// 最小费用最大流（mcmf）—— EK算法 + spfa

void reads(ll &x){ //读入优化（正负整数）
    ll f=1;x=0;char S=getchar();
    while(S<'0'||S>'9'){if(S=='-')f=-1;S=getchar();}
    while(S>='0'&&S<='9'){x=x*10+S-'0';S=getchar();}
    x*=f; //正负号
}

const ll N=100019;

struct edge{ ll ver,nextt,flow,cost; }e[2*N];

ll tot=-1,n,m,S,T,maxf=0,minc=0;

ll flow[N],head[N],dist[N],inq[N],pre[N],lastt[N];

void add(ll a,ll b,ll f,ll c)
{ e[++tot].nextt=head[a],head[a]=tot,
  e[tot].ver=b,e[tot].flow=f,e[tot].cost=c; } 

bool spfa(ll S,ll T){
    queue<ll> q;
    memset(inq,0,sizeof(inq));
    memset(flow,0x7f,sizeof(flow));
    memset(dist,0x7f,sizeof(dist));
    q.push(S),dist[S]=0,pre[T]=-1,inq[S]=1;
    while(!q.empty()){
        ll x=q.front(); q.pop(); inq[x]=0;
        for(ll i=head[x];i!=-1;i=e[i].nextt){
            if(e[i].flow>0&&dist[e[i].ver]>dist[x]+e[i].cost){
                dist[e[i].ver]=dist[x]+e[i].cost;
                pre[e[i].ver]=x,lastt[e[i].ver]=i;
                flow[e[i].ver]=min(flow[x],e[i].flow);
                if(!inq[e[i].ver])
                    q.push(e[i].ver),inq[e[i].ver]=1;
            }
        }
    } return pre[T]!=-1;
}

void mcmf(){
    while(spfa(S,T)){
        ll now=T; //↓↓最小费用最大流
        maxf+=flow[T],minc+=dist[T]*flow[T];
        while(now!=S){ //↓↓正边流量-，反边流量+
            e[lastt[now]].flow-=flow[T];
            e[lastt[now]^1].flow+=flow[T]; 
            //↑↑利用xor1“成对储存”的性质
            now=pre[now]; //维护前向边last，前向点pre
        }
    }
}

int main(){
    scanf("%lld%lld%lld%lld",&n,&m,&S,&T);
    memset(head,-1,sizeof(head)); 
    //注意：一定要把head和tot初始化为-1，才能使用xor 1的性质
    for(ll i=1,x,y,f,c;i<=m;i++){
        scanf("%lld%lld%lld%lld",&x,&y,&f,&c);
        add(x,y,f,c),add(y,x,0,-c);
    } mcmf(),printf("%lld %lld\n",maxf,minc);
}

 

 二分图匹配的网络流算法

 

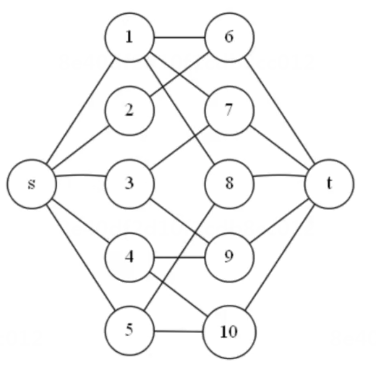
 最大流最小割问题