【暖*墟】#洛谷网课1.28# 省选数据结构
平衡树
全称“平衡二叉搜索树”。常见类型有：
Splay；Treap；AVL Tree；Red Black Tree；Scape Goat Tree...
二叉搜索树（BST）
---> 二叉搜索树的中序遍历是一个关键码单调递增的节点序列。
（1）BST的建立
为了避免越界，额外建立两个节点，关键码分别为正无穷和负无穷。
我们在开始的时候要建立只由这两个节点构成的一棵BST，称为一棵“初始BST”。
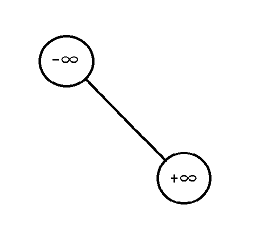
//建立初始BST struct BST{ int l,r; //左右子节点在数组中的下标 int val; //节点关键码 }a[N]; //数组模拟链表 int tot,root; //节点数 和 根节点编号 int New(int val) //新加节点 { a[++tot].val=val; return tot; } //返回节点编号 void Build(){ New(-INF),New(INF); //初始BST的节点 root=1; a[1].r=2; //如图设置根节点和右儿子 }
（2）BST的检索
即：在BST中查询是否存在关键码为val的节点。
设变量p等于根节点root，执行以下过程：
1.若p的关键码等于val，则已经找到。
2.若p的关键码大于val，那么有两种可能性：
(1) 若p的左子节点为空，则在此BST中没有val节点。
(2) 若p的左子节点不为空，就在p的左子树中递归查找。
3.若p的关键码小于val，那么也有两种可能性：
(1) 若p的右子节点为空，则在此BST中没有val节点。
(2) 若p的左右子节点不为空，就在p的右子树中递归查找。
---->
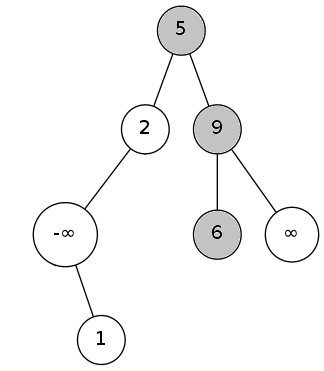如上图，查找6,6存在；查找3,3不存在。
int Get(int p,int val){ if(p==0) return 0; //不存在 if(val==a[p].val) return p; //找到了 if(val<a[p].val) return Get(a[p].l,val); else return Get(a[p].r,val); //递归左右子树 }
（3）BST的插入
即：在原BST中新加一个节点，值为val。
暂且认为原BST中不存在值为val的节点，设变量p等于root，然后执行：
1.若p的关键码大于val，就在p的左子树中递归查找新建点的位置。
2.若p的关键码小于val，就在p的右子树中递归查找新建点的位置。
3.在发现要走向的p的子节点为空，说明val不存在时，直接建立关键码为val的新节点为p的子节点。
插入3、8的过程
void Insert(int &p,int val){ //↑↑注意p是引用，其父节点的l或r的值会被同时更新 if(p==0){ p=New(val); return; } if(p<a[p].val) Insert(a[p].l,val); else Insert(a[p].r,val); }
（4）BST求前驱/后继
- 前驱：BST中val节点的前驱，即值小于val的前提下最大的数（关键码）
- 后继：BST中val节点的前驱，即值大于val的前提下最小的数（关键码）
检索后继：初始化ans为具有正无穷关键码的那个节点的编号。在BST中检索val的位置。
在检索的过程中，每经过一个节点，都检查该节点的关键码，判断能否更新所求的后继ans。
检索完成后，有三种可能的结果：
1.没有找到val。此时val的后继就在已经经过的节点中，ans即为所求。
2.找到了关键码为val的节点p，但p没有右子树。与上一种情况相同，ans即为所求。
3.找到了关键码为val的节点p，且p有右子树。从p的右子节点出发，一直向左走。
int GetNext(int val){ int ans=2; //a[2].val=INF int p=root; while(p){ if(val==a[p].val){ //检索成功 if(a[p].r>0){ //有右子树 p=a[p].r; while(a[p].l>0) p=a[p].l; ans=p; //↑↑从右子节点出发，一直向左走 } break; //退出while } if(a[p].val<val&&a[p].val>a[ans].val) ans=p; p=val<a[p].val?a[p].l:a[p].r; //每经过一个节点，尝试更新后继 } return ans; //↑↑不停向下，寻找val节点的位置 }
检索前驱的过程与后继相似：
int GetPre(int val){ int ans=1; //a[1].val=-INF int p=root; while(p){ if(val==a[p].val){ if(a[p].l>0){ p=a[p].l; while(a[p].r>0) p=a[p].r; //从左子树上一直向右走 ans=p; } break; } if(a[p].val<val&&a[p].val>a[ans].val) ans=p; p=val<a[p].val?a[p].l:a[p].r; } return ans; }
（5）BST的节点删除
即：从BST中删除关键码为val的节点。先在BST中检索val，得到节点p。
若p的子节点个数小于2，则直接删除p，并令p的子节点代替p的位置，与p的父节点相连。
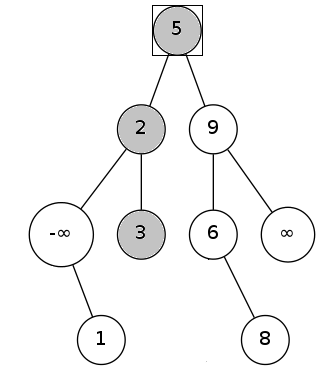
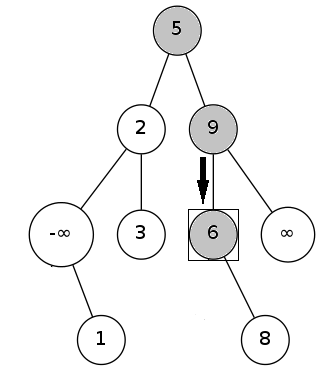
若p既有左子树又有右子树，则在BST中求出val的后继节点nxt。
因为nxt没有左子树，所以直接删除nxt，并令nxt的右子树代替nxt的位置。最后，再让nxt节点代替p节点，删除p即可。
--->
如上图，删除5，5的后继6代替5，6的右子树8代替6。
void Remove(int val){ int &p=root;//检索节点val，得到节点p while(p){ if(a[p].val==p) break; if(val<a[p].val) p=a[p].l; else p=a[p].r; } if(p==0) return; if(a[p].l==0) //没有左子树 p=a[p].r; //右子树代替p的位置，注意p是引用 else if(a[p].r==0) //没有右子树 p=a[p].l; //左子树代替p的位置，注意p是引用 else{ //既有左子树又有右子树 int nxt=a[p].r; //求后继节点 while(a[nxt].l>0) nxt=a[nxt].l; Remove(a[nxt].val); //nxt一定没有左子树，直接删除 a[nxt].l=a[p].l,a[nxt].r=a[p].r; //nxt代替节点p的位置 p=nxt; //注意p是引用 } }
Treap（树堆）
Treap的旋转
Treap只需要单旋，每个节点可能左旋或者右旋。
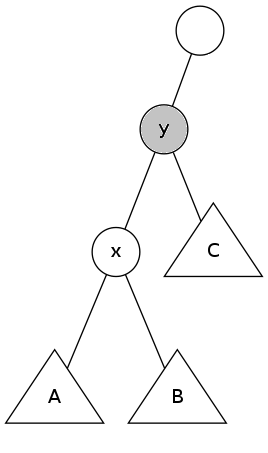右旋zig(y)-->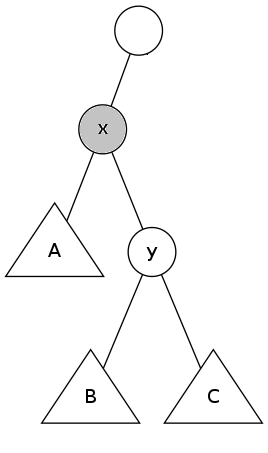
将右旋后的树再进行左旋又得到了原树。
以右旋为例。一开始x是y的左子节点，A和B分别是x的左右子树，C是y的右子树。
“右旋”操作在保持BST性质的基础上，把x变为y的父节点。
因为x的关键码小于y的关键码，所以y应该作为x的右子节点。
当x变成y的父节点后，y的左子树就空了出来，于是x原来的右子树B就恰好作为y的左子树。
右旋操作的代码如下，zig(p)可以理解为把p的左子节点绕着p向右旋转：
void zig(int &p) //注意p是引用 { int q=a[p].l; a[p].l=a[q].r,a[q].r=p,p=q; }
左旋操作的代码如下，zag(p)可以理解为把p的右子节点绕着p向左旋转：
void zag(int &p) //注意p是引用 { int q=a[p].r; a[p].r=a[q].l,a[q].l=p,p=q; }
合理的旋转操作可使BST变得更“平衡”。如下图，对链进行一系列操作。
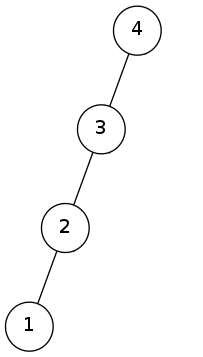右旋zig(3) --> 
再右旋zig(4)-->
Treap在插入每个新节点时，给该节点随机生成一个额外的权值。
像二叉堆的插入过程一样，Treap在插入时、自底向上依次检查。
当某个节点不满足大根堆性质时，就执行单旋，使该点与其父节点的关系发生对换。
Treap通过单旋，维持节点关键码满足BST性质，还使每个节点上随机生成的额外权值满足大根堆性质。
Treap是一种平衡二叉搜索树，检查、插入、求前驱后继以及删除节点的时间复杂度都是O(logN)。
Treap的插入
Treap的删除
特别地，对于删除操作，可以直接找到需要删除的节点，并把它向下旋转成叶节点直接删除 。
这样就避免了采取类似普通BST的删除方法可能导致的节点信息更新、堆性质维护等复杂问题。
【例题】洛谷p3369 普通平衡树
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<string> #include<queue> #include<vector> #include<cmath> #include<map> using namespace std; typedef long long ll; /*【p3369】普通平衡树 维护一些数，其中需要提供以下操作： 1. 插入x数 2. 删除x数(若有多个相同的数，因只删除一个) 3. 查询x数的排名(若有多个相同的数，因输出最小的排名) 4. 查询排名为x的数 5. 求x的前驱(前驱定义为小于x，且最大的数) 6. 求x的后继(后继定义为大于x，且最小的数) */ //【Treap模板题】 //对于有重复的数字，给每个节点增加一个cnt[]， //记录与该节点相同的数字的个数，可以成为该节点的“副本数”。 //插入相同值cnt++，删除则cnt--，直到cnt=0时删除该点。 void reads(int &x){ //读入优化（正负整数） int fa=1;x=0;char s=getchar(); while(s<'0'||s>'9'){if(s=='-')fa=-1;s=getchar();} while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+s-'0';s=getchar();} x*=fa; //正负号 } const int INF=0x7fffffff,N=100019; int n,tot=0,root; struct Treap{ int l,r,val,dat,cnt,siz; }a[N]; //左右儿子、节点关键码、权值（优先级）、副本数、子树大小 int New(int x) //新建节点（！=插入固定值） { a[++tot].val=x,a[tot].dat=rand(); //treap随机权值 a[tot].cnt=a[tot].siz=1; return tot; } void Update(int p) //随时更新并统计子树大小 { a[p].siz=a[a[p].l].siz+a[a[p].r].siz+a[p].cnt; } void Build() //建立初始BST树 { New(-INF),New(INF),root=1,a[1].r=2,Update(root); } int GetRankByVal(int p,int k){ if(p==0) return 0; //由排名找编号val if(k==a[p].val) return a[a[p].l].siz+1; else if(k<a[p].val) return GetRankByVal(a[p].l,k); else return GetRankByVal(a[p].r,k)+a[a[p].l].siz+a[p].cnt; } int GetValByRank(int p,int rank){ if(p==0) return INF; //由编号val找排名 if(a[a[p].l].siz>=rank) return GetValByRank(a[p].l,rank); else if(a[a[p].l].siz+a[p].cnt>=rank) return a[p].val; else return GetValByRank(a[p].r,rank-a[a[p].l].siz-a[p].cnt); } void zig(int &p){ //右旋 int q=a[p].l; a[p].l=a[q].r,a[q].r=p,p=q; Update(a[p].r),Update(p); } //注意update修改顺序 void zag(int &p){ //左旋 int q=a[p].r; a[p].r=a[q].l,a[q].l=p,p=q; Update(a[p].l),Update(p); } //注意update修改顺序 void Insert(int &p,int k){ //插入结点 if(p==0){ p=New(k); return; } //找到对应位置，新建节点 if(k==a[p].val){ a[p].cnt++,Update(p); return; } if(k<a[p].val){ Insert(a[p].l,k); //↑↑节点已存在，个数++ if(a[p].dat<a[a[p].l].dat) zig(p); } //维护堆的平衡 else{ Insert(a[p].r,k); if(a[p].dat>a[a[p].r].dat) zag(p); } Update(p); //递归修改子树大小 } void Remove(int &p,int k){ //删除操作 if(p==0) return; if(k==a[p].val){ //找到这个节点 if(a[p].cnt>1) //减小cnt { a[p].cnt--,Update(p); return; } if(a[p].l||a[p].r){ //非叶子节点，向下旋转 if(a[p].r==0||a[a[p].l].dat>a[a[p].r].dat) zig(p),Remove(a[p].r,k); else zag(p),Remove(a[p].l,k); Update(p); //递归修改子树大小 } else p=0; return; //旋转到叶子节点再删除 } if(k<a[p].val) Remove(a[p].l,k); //向下寻找val=k的节点 else Remove(a[p].r,k); Update(p); //递归修改子树大小 } int GetPre(int k){ int ans=1,p=root; while(p){ if(k==a[p].val){ if(a[p].l>0){ p=a[p].l; while(a[p].r>0) p=a[p].r; ans=p; } break; } if(a[p].val<k&&a[p].val>a[ans].val) ans=p; if(k<a[p].val) p=a[p].l; else p=a[p].r; } return a[ans].val; } int GetNxt(int k){ int ans=2,p=root; while(p){ if(k==a[p].val){ if(a[p].r>0){ p=a[p].r; while(a[p].l>0) p=a[p].l; ans=p; } break; } if(a[p].val>k&&a[p].val<a[ans].val) ans=p; if(k<a[p].val) p=a[p].l; else p=a[p].r; } return a[ans].val; } int main(){ scanf("%d",&n); Build(); while(n--){ int x,k; scanf("%d%d",&k,&x); if(k==1) Insert(root,x); if(k==2) Remove(root,x); if(k==3) printf("%d\n",GetRankByVal(root,x)-1); if(k==4) printf("%d\n",GetValByRank(root,x+1)); if(k==5) printf("%d\n",GetPre(x)); if(k==6) printf("%d\n",GetNxt(x)); } }
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<string> #include<queue> #include<vector> #include<cmath> #include<map> #include<set> using namespace std; typedef long long ll; /*【p2234】营业额统计 维护每天最小波动值=min{|该天以前某一天的营业额-该天营业额|}的sum。*/ //【treap】一天天插入数字，查询前驱和后继累加最小波动值。 void reads(int &x){ //读入优化（正负整数） int fa=1;x=0;char s=getchar(); while(s<'0'||s>'9'){if(s=='-')fa=-1;s=getchar();} while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+s-'0';s=getchar();} x*=fa; //正负号 } const int N=2e5+19,inf=1e9+19; struct node{ int l,r,v,siz,rnd,w; }tree[N]; //v为权值,rnd为堆的优先级（随机值）,w为v的个数 int n,sz,root,ans,ans1,a[N]; void update(int pos) { tree[pos].siz=tree[tree[pos].l].siz+tree[tree[pos].r].siz+tree[pos].w; } void lturn(int &pos){ int t=tree[pos].r; tree[pos].r=tree[t].l; tree[t].l=pos,tree[t].siz=tree[pos].siz; update(pos),pos=t; } void rturn(int &pos){ int t=tree[pos].l; tree[pos].l=tree[t].r; tree[t].r=pos,tree[t].siz=tree[pos].siz; update(pos),pos=t; } void insert(int &k,int x){ if(k==0){ sz++; k=sz; tree[k].w=tree[k].siz=1; tree[k].rnd=rand(); tree[k].v=x; return; } tree[k].siz++; if(tree[k].v==x) tree[k].w++; else if(tree[k].v>x){ insert(tree[k].l,x); if(tree[tree[k].l].rnd>tree[k].rnd) rturn(k); } else{ insert(tree[k].r,x); if(tree[tree[k].r].rnd>tree[k].rnd) lturn(k); } } void query(int pos,int x){ //查询前驱 if(pos==0) return; if(tree[pos].v<=x) ans=tree[pos].v,query(tree[pos].r,x); else query(tree[pos].l,x); } void query1(int pos,int x){ //查询后继 if(pos==0) return; if(tree[pos].v>x) ans1=tree[pos].v,query1(tree[pos].l,x); else query1(tree[pos].r,x); } int main(){ reads(n); for(int i=1;i<=n;i++) reads(a[i]); int sum=a[1]; insert(root,a[1]); for(int i=2;i<=n;i++){ ans=2*inf,ans1=2*inf; query(root,a[i]),query1(root,a[i]); if(ans1==2*inf) sum+=abs(a[i]-ans); //没有后继 else if(ans==2*inf) sum+=abs(a[i]-ans1); //没有前驱 else sum+=min(abs(a[i]-ans1),abs(a[i]-ans)); insert(root,a[i]); //一天天处理，放入treap中 } printf("%d\n",sum); return 0; }
#include <cmath> #include <iostream> #include <cstdio> #include <string> #include <cstring> #include <vector> #include <algorithm> #include <queue> #include <stack> using namespace std; typedef long long ll; typedef unsigned long long ull; #define R register /*【p4309】最长上升子序列 给定一个序列，初始为空。将1到N的每个数字依次插入到特定的位置。 每插入一个数字，想知道此时最长上升子序列长度是多少？*/ //设f[i]表示插入的数/插入个数是i的时候的LIS长度。 //由于是从小到大插入的，所以后插入的数不会影响先插入的数的ans。 void reads(int &x){ //读入优化（正负整数） int f=1;x=0;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} x*=f; //正负号 } const int N=100019; int n,v,ch[N][2],sz,P[N],siz[N],a[N],f[N],c[N],t,maxx; //------------平衡树部分-------------// void Pushup(int u){ siz[u]=siz[ch[u][0]]+siz[ch[u][1]]+1; } void Dfs(int u){ if(!u) return; Dfs(ch[u][0]); a[++t]=u; Dfs(ch[u][1]); } void Rotate(int &u,int d){ ch[u][d]=ch[v=ch[u][d]][d^1]; ch[v][d^1]=u; u=v; } void Insert(int &u,int pos){ if(!u){ siz[u=++sz]=1; P[u]=rand(); return; } int d=siz[ch[u][0]]<pos; siz[u]++; Insert(ch[u][d],d?pos-1-siz[ch[u][0]]:pos); if(P[u]<P[ch[u][d]]) Rotate(u,d),Pushup(ch[u][d^1]),Pushup(u); } //------------树状数组部分-------------// void ADD(int x,int d){ while(x<=n) c[x]=max(c[x],d),x+=x&-x; } void Get(int x){ maxx=0; while(x) maxx=max(maxx,c[x]),x-=x&-x; return; } //------------主程序部分-------------// int main(){ scanf("%d",&n);int root=0; for(int i=1;i<=n;i++) scanf("%d",&v),Insert(root,v); Dfs(root); for(int i=1;i<=n;i++) //树状数组维护，求出dp答案 Get(a[i]),ADD(a[i],f[a[i]]=maxx+1); for(int i=1;i<=n;i++) f[i]=max(f[i],f[i-1]),printf("%d\n",f[i]); }
Splay（伸展树）
主要思想：对于查找频率较高的节点，使其处于离根节点相对较近的位置。
这样就可以保证查找效率。Splay是平衡树的一种，中文名为伸展树。
- 什么样的点是查找频率高的点？
- 怎么实现把节点搬到根这种操作？
Rotate操作
如果要把一个点挪到根，那我们首先要知道怎么让一个点挪到它的父节点。
情况1：X是Y的左孩子
---->
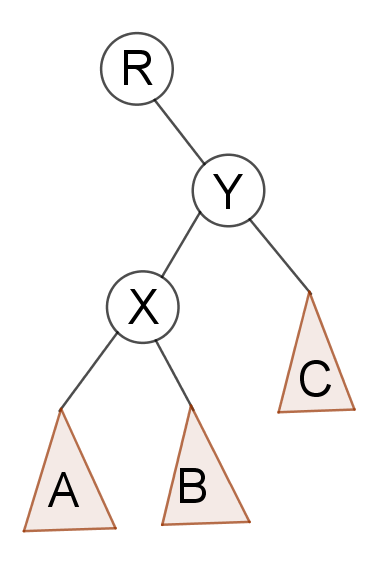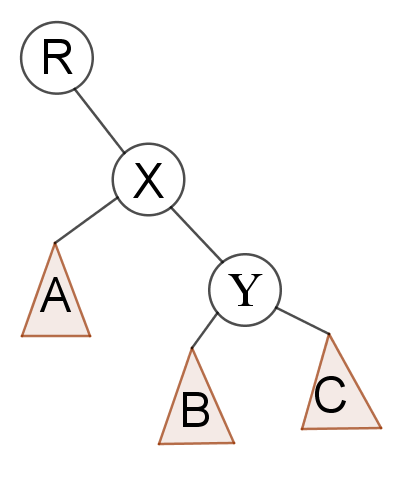
这时候如果我们让X成为Y的父亲，只会影响到3个点的关系。
即： B与X，X与Y，X与R。根据二叉排序树的性质：
B会成为Y的左儿子，Y会成为X的右儿子，X会成为R的儿子（=Y是R的某儿子）。
情况2：X是Y的右孩子
----> 
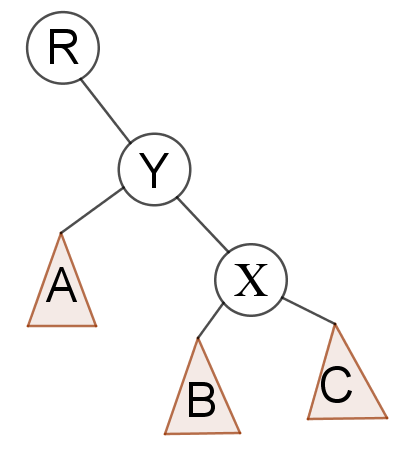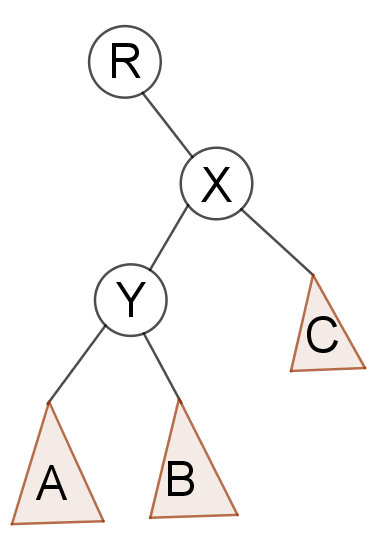
二者本质相同，旋转情况很类似，第二种情况实际就是把第一种情况的X,Y换了换位置。
考虑能否将这两种情况合并起来实现呢？答案是肯定的。
首先我们要获取到每一个节点是它父亲的哪个孩子，可以这么写：
bool ident(int x){ return tree[tree[x].fa].ch[0] == x ? 0 : 1; }
左孩子会返回0，右孩子会返回1。可以得到 R，Y，X 这三个节点的信息。
int Y = tree[x].fa, R = tree[Y].fa; int Yson = ident(x), Rson = ident(Y); //↑↑ x是y的哪个孩子,y是R的哪个儿子
被影响的X儿子——节点B的情况，可以根据X的情况推算。^运算的性质，0^1=1,1^1=0,2^1=3,3^1=2...
B相对于X的位置、一定与X相对于Y的位置相反。（否则在旋转的过程中不会对B产生影响）
int B = tree[x].ch[Yson ^ 1];
考虑连接的过程。根据上面的图，不难得到：
- B成为Y的哪个儿子 与 X是Y的哪个儿子 相同 。
- Y成为X的哪个儿子 与 X是Y的哪个儿子 相反 。
- X成为R的哪个儿子 与 Y是R的哪个儿子 相同 。
void connect(int x, int fa, int how) //x节点将成为fa节点的how孩子 { tree[x].fa = fa, tree[fa].ch[how] = x; } connect(B, Y, Yson)，connect(Y, x, Yson ^ 1)，connect(x, R, Rson);
这就是一个单旋函数。利用这个函数就可以实现把一个节点搬到父亲的位置。
Splay操作
Splay(x,to)是实现把x节点搬到 to节点。最简单的办法：对于x节点，每次上旋，直到 to。
但这种单旋的方式很容易被卡死，如下图所示：
把一个点双旋到根，可以使得：
从根到它的路径上的所有点的深度变为大约原来的一半，其它点的深度最多增加2。
双旋的Splay，总的来说有三种情况：
1.to是x的父亲。（为了方别写，开始的时候把to设置为to的父亲）
if (tree[tree[x].fa].fa == to) rotate(x);
2.x 和他父亲 和他父亲的父亲 在一条线上。
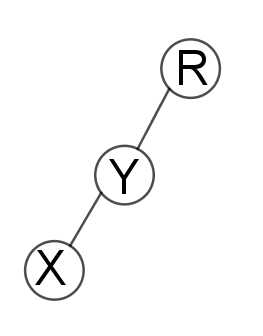这时候先把Y旋转上去，再把X旋转上去就好。
else if (ident(x) == ident(tree[x].fa)) rotate(tree[x].fa), rotate(x);
3.x 和他父亲 和他父亲的父亲 不在一条线上。
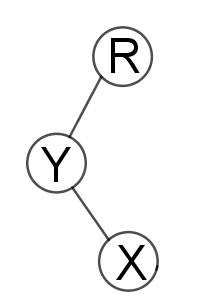这时候把X旋转两次就好。
三种情况的总体代码：
void splay(int x, int to) { to = tree[to].fa; //初始设为to的父亲 while (tree[x].fa != to) { if (tree[tree[x].fa].fa == to) rotate(x); //（1） else if (ident(x) == ident(tree[x].fa)) rotate(tree[x].fa), rotate(x); //（2） else rotate(x), rotate(x); //（3） } }
其余部分代码实现
//初始结构体 struct node { int v; //权值 int fa; //父亲节点 int ch[2]; //0代表左儿子，1代表右儿子 int rec; //这个权值的节点出现的次数 int siz; //子节点的数量 }; int tot;//tot表示不算重复的有多少节点
插入函数（Insert）
根据前面讲的，我们在插入一个数之后，需要将其旋转到根。
首先，当这棵树已经没有节点（到达叶子）的时候，直接新建一个节点。
int newnode(int v,int fa){ tree[++tot].fa=fa; tree[tot].v=v; //权值 tree[tot].sum=tree[tot].rec=1; return tot; }
当树有节点的时候，根据二叉查找树的性质，不断向下走，直到找到一个可以插入的点。
注意：在走的时候，需要更新每个节点的siz值（儿子++）。
void Insert(int x){ int now=root; if(root==0){ newnode(x,0);root=tot; } else{ while(1){ T[now].siz++; if(T[now].val==x) //找到权值为x的点，旋转至根节点 { T[now].rec++; splay(now,root); return; } int nxt=x<T[now].val?0:1; if(!T[now].ch[nxt]){ int p=newnode(x,now); T[now].ch[nxt]=p; splay(p,root); return ; } now=T[now].ch[nxt]; } } }
普通的Splay树都会用到的函数操作の代码总结：
#define ls(x) T[x].ch[0] #define rs(x) T[x].ch[1] #define fa(x) T[x].fa #define root T[0].ch[1] const int MAXN=100019,INF=(int)1e9+10; inline int read(){ char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } struct node{ int fa,ch[2],val,rec,siz; }T[MAXN]; int tot=0; void update(int x){T[x].siz=T[ls(x)].siz+T[rs(x)].siz+T[x].rec;} int ident(int x){return T[fa(x)].ch[0]==x?0:1;} void connect(int x,int fa,int how){T[fa].ch[how]=x;T[x].fa=fa;} void rotate(int x){ int Y=fa(x),R=fa(Y),Yson=ident(x),Rson=ident(Y); connect(T[x].ch[Yson^1],Y,Yson); connect(Y,x,Yson^1),connect(x,R,Rson); update(Y),update(x); } void splay(int x,int to){ to=fa(to); //to先初始化为to的fa while(fa(x)!=to){ int y=fa(x); if(T[y].fa==to) rotate(x); //(1) else if(ident(x)==ident(y)) rotate(y),rotate(x); //(2) else rotate(x),rotate(x); //(3) } } int newnode(int v,int fa_){ T[++tot].fa=fa_,T[tot].val=v; T[tot].rec=T[tot].siz=1; return tot; } void Insert(int x){ int now=root; //↓↓到达空节点(叶子) if(root==0){ newnode(x,0); root=tot; return; } while(1){ T[now].siz++; //路径上经过的每个节点的叶子数++ if(T[now].val==x){ T[now].rec++; splay(now,root); return; } int nxt=x<T[now].val?0:1; //继续寻找可以放置x节点的位置 if(!T[now].ch[nxt]){ int p=newnode(x,now); T[now].ch[nxt]=p; splay(p,root); return; } now=T[now].ch[nxt]; //未找到空位，继续向下走 } }
删除函数（Delet）
即：先找到权值为 v 的节点的位置，把找到的节点splay到根，再删除。
int find(int x){ //用于dele函数和查询排名 int now=root; //从根节点开始查找 while(1){ if(!now) return 0; if(T[now].val==x){ splay(now,root); return now; } int nxt=x<T[now].val?0:1; now=T[now].ch[nxt]; //向下找 } }
怎样才能保证删除节点后整棵树还满足二叉查找树的性质？
- 权值为v的节点个数>1：直接把它的rec和sum减去1。
- 本节点没有左右儿子：成为一棵空树，root=0即删除它。
- 本节点没有左儿子：直接把他的右儿子设置成根。
- 既有左儿子，又有右儿子：在它的左儿子中找到最大的，旋转到根，
- 把它的右儿子当做根(也就是它最大的左儿子)的右儿子。
void delet(int x){ int pos=find(x); if(!pos) return; if(T[pos].rec>1){ T[pos].rec--,T[pos].sum--; return; } if(!T[pos].ch[0]&&!T[pos].ch[1]){ root=0; return; } //空树 if(!T[pos].ch[0]){ root=T[pos].ch[1]; T[root].fa=0; return; } //↑↑本节点没有左儿子：直接把他的右儿子设置成根，就相当于删除了它 int left=T[pos].ch[0]; while(T[left].ch[1]) left=T[left].ch[1]; //↑↑在它的左子树中不断递归右儿子，找到权值最大的节点 splay(left,T[pos].ch[0]); //旋转到根，维护平衡树 connect(T[pos].ch[1],left,1),connect(left,0,1),update(left); }
查询x数的排名
int rak(int val){ int pos=find(val); return T[ls(pos)].siz+1; }
查询排名为x的数
用used变量记录该节点以及它的左子树有多少节点。
如果x>左子树的数量且<used，那么当前节点的权值就是答案；否则根据性质继续向下走。
int arank(int x){ //查询排名为x的数是什么 int now=root; while(1){ int used=tree[now].sum-tree[tree[now].ch[1]].sum; if(x>tree[tree[now].ch[0]].sum&&x<=used) break; if(x<used) now=tree[now].ch[0]; else x=x-used,now=tree[now].ch[1]; } splay(now,root); return tree[now].v; }
求x的前驱后继
可以维护一个ans变量，然后对整棵树进行遍历，同时更新ans。
int lower(int v) // 小于v的最大值 { int now=root , ans=-maxn; while(now){ if(tree[now].v<v&&tree[now].v>ans) ans=tree[now].v; if(v>tree[now].v) now=tree[now].ch[1]; else now=tree[now].ch[0]; } return ans; } int upper(int v) // 大于v的最小值 { int now=root , ans=maxn; while(now){ if(tree[now].v>v&&tree[now].v<ans) ans=tree[now].v; if(v<tree[now].v) now=tree[now].ch[0]; else now=tree[now].ch[1]; } return ans; }
【例题】普通平衡树的Splay实现
#include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #define ls(x) T[x].ch[0] #define rs(x) T[x].ch[1] #define fa(x) T[x].fa #define root T[0].ch[1] using namespace std; const int MAXN=1e5+10,mod=10007,INF=1e9+10; inline int read()
{
char c=getchar();int x=0,f=1;
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
} struct node{ int fa,ch[2],val,rec,sum; }T[MAXN]; int tot=0,pointnum=0; void update(int x){T[x].sum=T[ls(x)].sum+T[rs(x)].sum+T[x].rec;} int ident(int x){return T[fa(x)].ch[0]==x?0:1;} void connect(int x,int fa,int how){T[fa].ch[how]=x;T[x].fa=fa;} void rotate(int x) { int Y=fa(x),R=fa(Y); int Yson=ident(x),Rson=ident(Y); connect(T[x].ch[Yson^1],Y,Yson); connect(Y,x,Yson^1); connect(x,R,Rson); update(Y);update(x); } void splay(int x,int to) { to=fa(to); while(fa(x)!=to) { int y=fa(x); if(T[y].fa==to) rotate(x); else if(ident(x)==ident(y)) rotate(y),rotate(x); else rotate(x),rotate(x); } } int newnode(int v,int f) { T[++tot].fa=f; T[tot].rec=T[tot].sum=1; T[tot].val=v; return tot; } void Insert(int x) { int now=root; if(root==0) {newnode(x,0);root=tot;} else { while(1) { T[now].sum++; if(T[now].val==x) {T[now].rec++;splay(now,root);return ;} int nxt=x<T[now].val?0:1; if(!T[now].ch[nxt]) { int p=newnode(x,now); T[now].ch[nxt]=p; splay(p,root);return ; } now=T[now].ch[nxt]; } } } int find(int x) { int now=root; while(1) { if(!now) return 0; if(T[now].val==x) {splay(now,root);return now;} int nxt=x<T[now].val?0:1; now=T[now].ch[nxt]; } } void delet(int x) { int pos=find(x); if(!pos) return ; if(T[pos].rec>1) {T[pos].rec--,T[pos].sum--;return ;} else { if(!T[pos].ch[0]&&!T[pos].ch[1]) {root=0;return ;} else if(!T[pos].ch[0]) {root=T[pos].ch[1];T[root].fa=0;return ;} else { int left=T[pos].ch[0]; while(T[left].ch[1]) left=T[left].ch[1]; splay(left,T[pos].ch[0]); connect(T[pos].ch[1],left,1); connect(left,0,1); update(left); } } } int rak(int x) { int now=root,ans=0; while(1) { if(T[now].val==x) return ans+T[T[now].ch[0]].sum+1; int nxt=x<T[now].val?0:1; if(nxt==1) ans=ans+T[T[now].ch[0]].sum+T[now].rec; now=T[now].ch[nxt]; } } int kth(int x)//排名为x的数 { int now=root; while(1) { int used=T[now].sum-T[T[now].ch[1]].sum; if(T[T[now].ch[0]].sum<x&&x<=used) {splay(now,root);return T[now].val;} if(x<used) now=T[now].ch[0]; else now=T[now].ch[1],x-=used; } } int lower(int x) { int now=root,ans=-INF; while(now) { if(T[now].val<x) ans=max(ans,T[now].val); int nxt=x<=T[now].val?0:1;//这里需要特别注意 now=T[now].ch[nxt]; } return ans; } int upper(int x) { int now=root,ans=INF; while(now) { if(T[now].val>x) ans=min(ans,T[now].val); int nxt=x<T[now].val?0:1; now=T[now].ch[nxt]; } return ans; } int main(){ int N=read(); while(N--) { int opt=read(),x=read(); if(opt==1) Insert(x); else if(opt==2) delet(x); else if(opt==3) printf("%d\n",rak(x)); else if(opt==4) printf("%d\n",kth(x)); else if(opt==5) printf("%d\n",lower(x)); else if(opt==6) printf("%d\n",upper(x)); } }
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<string> #include<queue> #include<vector> #include<cmath> #include<map> using namespace std; typedef long long ll; #define ls(x) T[x].ch[0] #define rs(x) T[x].ch[1] #define fa(x) T[x].fa #define root T[0].ch[1] /*【p3871】中位数 add a 在序列末尾添加一个整数a；mid 输出此时的中位数。 */ const int MAXN=100019,INF=(int)1e9+10; inline int read(){ char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } struct node{ int fa,ch[2],val,rec,siz; }T[MAXN]; int tot=0,cnt=0; void update(int x){T[x].siz=T[ls(x)].siz+T[rs(x)].siz+T[x].rec;} int ident(int x){return T[fa(x)].ch[0]==x?0:1;} void connect(int x,int fa,int how){T[fa].ch[how]=x;T[x].fa=fa;} void rotate(int x){ int Y=fa(x),R=fa(Y); int Yson=ident(x),Rson=ident(Y); connect(T[x].ch[Yson^1],Y,Yson); connect(Y,x,Yson^1),connect(x,R,Rson); update(Y),update(x); } void splay(int x,int to){ to=fa(to); //to先初始化为to的fa while(fa(x)!=to){ int y=fa(x); if(T[y].fa==to) rotate(x); //(1) else if(ident(x)==ident(y)) rotate(y),rotate(x); //(2) else rotate(x),rotate(x); //(3) } } int newnode(int v,int fa_){ T[++tot].fa=fa_,T[tot].val=v; T[tot].rec=T[tot].siz=1; return tot; //返回节点编号 } void Insert(int x){ int now=root; //↓↓到达空节点(叶子) if(root==0){ newnode(x,0); root=tot; return; } while(1){ T[now].siz++; //路径上经过的每个节点的叶子数++ if(T[now].val==x){ T[now].rec++; splay(now,root); return; } int nxt=x<T[now].val?0:1; //继续寻找可以放置x节点的位置 if(!T[now].ch[nxt]){ int p=newnode(x,now); T[now].ch[nxt]=p; splay(p,root); return; } now=T[now].ch[nxt]; //未找到空位，继续向下走 } } int kth(int x){ //排名为x的数 int now=root; while(1){ int used=T[now].siz-T[T[now].ch[1]].siz; if(T[T[now].ch[0]].siz<x&&x<=used) { splay(now,root); return T[now].val; } if(x<used) now=T[now].ch[0]; else now=T[now].ch[1],x-=used; } } int main(){ int N=read(); Insert(INF); Insert(-INF); for(int i=1;i<=N;i++) Insert(read()),cnt++; char op[19]; int M=read(); //m次操作 for(int i=1;i<=M;i++){ cin>>op; if(op[0]=='a') Insert(read()),cnt++; if(op[0]=='m'){ int mid_=cnt/2+1; if(cnt%2==1) printf("%d\n",kth(mid_+1)); else printf("%d\n",min(kth(mid_),kth(mid_+1))); } } }
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<string> #include<queue> #include<vector> #include<cmath> #include<map> using namespace std; typedef long long ll; #define ls(x) T[x].ch[0] #define rs(x) T[x].ch[1] #define fa(x) T[x].fa #define root T[0].ch[1] /*【p2286】宠物收养场 */ // splay求前驱后继 + splay删除 + 分类讨论技巧 const int N=100019,mod=1000000; inline int read(){ char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } struct node{ int fa,ch[2],val,rec; }T[N]; int tot=0; int ident(int x){return T[fa(x)].ch[0]==x?0:1;} void connect(int x,int fa,int how){T[fa].ch[how]=x;T[x].fa=fa;} void rotate(int x){ int Y=fa(x),R=fa(Y); int Yson=ident(x),Rson=ident(Y); connect(T[x].ch[Yson^1],Y,Yson); connect(Y,x,Yson^1),connect(x,R,Rson); } void splay(int x,int to){ to=fa(to); //to先初始化为to的fa while(fa(x)!=to){ int y=fa(x); if(T[y].fa==to) rotate(x); //(1) else if(ident(x)==ident(y)) rotate(y),rotate(x); //(2) else rotate(x),rotate(x); //(3) } } int newnode(int v,int fa_){ T[++tot].fa=fa_,T[tot].val=v,T[tot].rec=1; return tot; //返回节点编号 } void insert(int x){ int now=root; //↓↓到达空节点(叶子) if(root==0){ newnode(x,0); root=tot; return; } while(1){ if(T[now].val==x){ T[now].rec++; splay(now,root); return; } int nxt=x<T[now].val?0:1; //继续寻找可以放置x节点的位置 if(!T[now].ch[nxt]){ int p=newnode(x,now); T[now].ch[nxt]=p; splay(p,root); return; } now=T[now].ch[nxt]; //未找到空位，继续向下走 } } int find(int x){ //用于dele函数和查询排名 int now=root; while(now){ if(T[now].val==x){ splay(now,root); return now; } int nxt=x<T[now].val?0:1; now=T[now].ch[nxt]; //向下找 } } void dele(int x){ int pos=find(x); if(!pos) return; if(T[pos].rec>1){ T[pos].rec--; return; } if(!T[pos].ch[0]&&!T[pos].ch[1]){ root=0; return; } //空树 if(!T[pos].ch[0]){ root=T[pos].ch[1]; T[root].fa=0; return; } //↑↑本节点没有左儿子：直接把他的右儿子设置成根，就相当于删除了它 int left=T[pos].ch[0]; while(T[left].ch[1]) left=T[left].ch[1]; //↑↑在它的左子树中不断递归右儿子，找到权值最大的节点 splay(left,T[pos].ch[0]); //旋转到根，维护平衡树 connect(T[pos].ch[1],left,1),connect(left,0,1); } int lower(int x){ int now=root,ans=-2e9; while(now){ if(T[now].val<x) ans=max(ans,T[now].val); int nxt=(x<=T[now].val)?0:1; now=T[now].ch[nxt]; } return ans; //↑↑注意这里要写等号 } int upper(int x){ int now=root,ans=2e9; while(now){ if(T[now].val>x) ans=min(ans,T[now].val); int nxt=(x<T[now].val)?0:1; now=T[now].ch[nxt]; } return ans; //↑↑注意这里不写等号 } int main(){ int n=read(),ans=0,PetNum=0; while(n--){ int opt=read(),x=read(); if(PetNum==0){ insert(x); //平衡状态 if(opt==0) PetNum++; //宠物++ else PetNum--; //领养者++(反向负数加) } else if(PetNum>0){ //宠物多 if(opt==0) insert(x),PetNum++; else{ int pre=lower(x),lat=upper(x); if(abs(pre-x)<=abs(x-lat)) dele(pre),ans=(ans+abs(pre-x))%mod; else dele(lat),ans=(ans+abs(lat-x))%mod; PetNum--; } } else if(PetNum<0){ //领养者多 if(opt==1) insert(x),PetNum--; else{ int pre=lower(x),lat=upper(x); if((abs(pre-x))<abs(x-lat)) dele(pre),ans=(ans+abs(pre-x))%mod; else dele(lat),ans=(ans+abs(lat-x))%mod; PetNum++; } } } printf("%d\n",ans); return 0; }
Splay处理区间问题
l,r
