【暖*墟】 #数据结构进阶# 点分治
点分治,是一种处理树上路径问题的工具,适用于树上的求和问题。
给定一棵树和一个整数k,求 树上边数等于k的路径 有多少条。
做法1:枚举不同的两个点,用dfs算出距离、并统计求值。O(n^3)。
做法2:找根,求出每个点到根的距离,枚举两点求lca。O(n^2logn)。
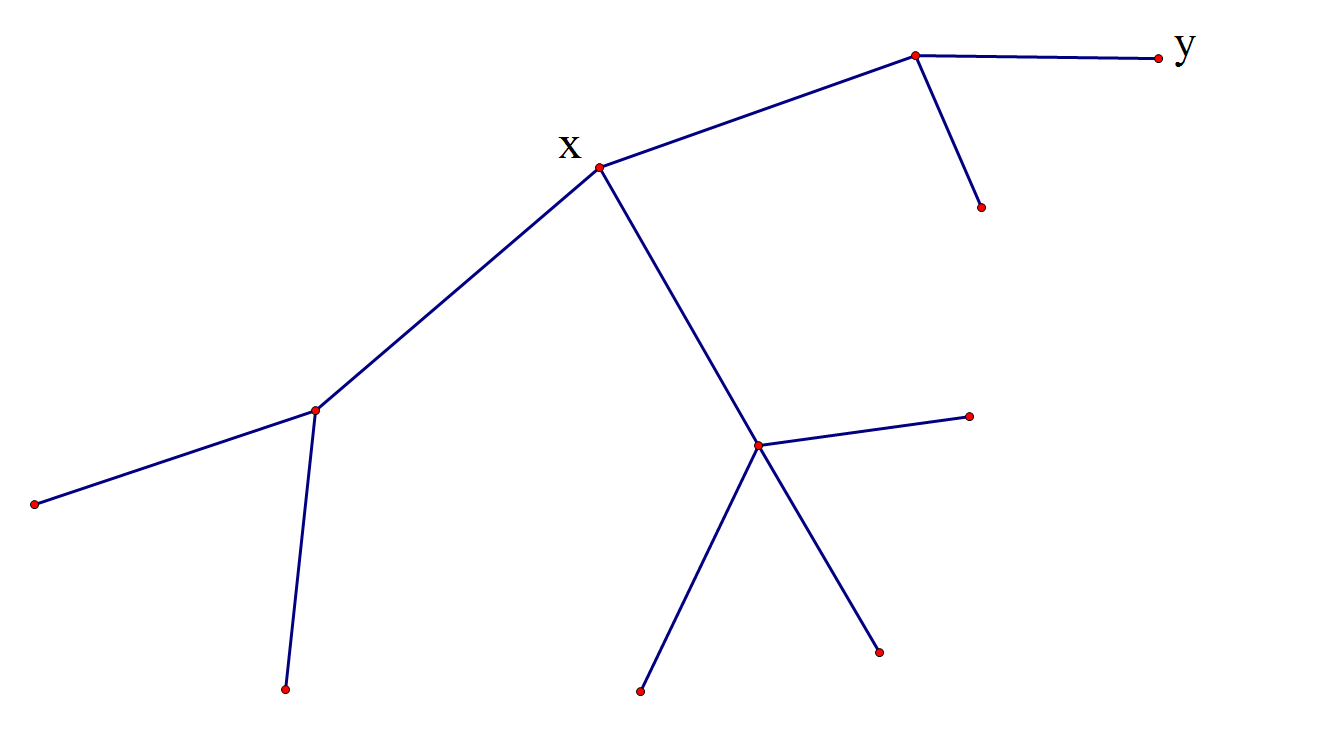
做法3:考虑形成路径的情况,假设一条满足条件的路径经过点x,
那么这条路径 ①在x的一个子树里(以x为端点) 或者 ②在x的两个不同的子树里。
 dfs遍历子树中的每个点,依次处理每个点的子树答案。
dfs遍历子树中的每个点,依次处理每个点的子树答案。
点分治的算法流程:
- 对于当前的这一部分树,求出当前这一部分的重心;
- 维护当前重心为根时、对应的答案,统计求和;
- 去掉当前重心,将当前这部分树分成更多部分,重复如上操作。
点分治的一个简单性质:
- 因为每次都以重心分割树,所以当前层每条经过重心的路径都是以前没枚举到过的。
- 即:每个重心管辖范围内经过重心的路径条数之和,就是树上的所有路径。
原理(左右子树分治)
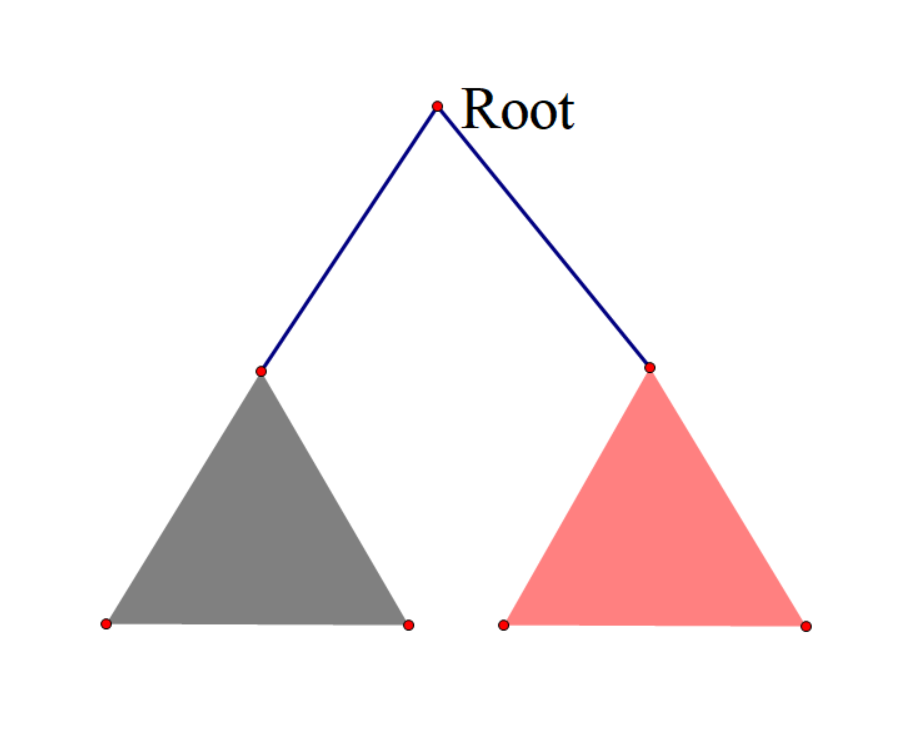
假设我们选出一个根Root,那么答案路径肯定是:
- 被左子树或右子树完全包含;
- 两子树中各选一部分路径,从Root处拼起来。
思考发现情况1(被一个子树包含)中,答案路径上的某点可以看成新的根,即Root2。
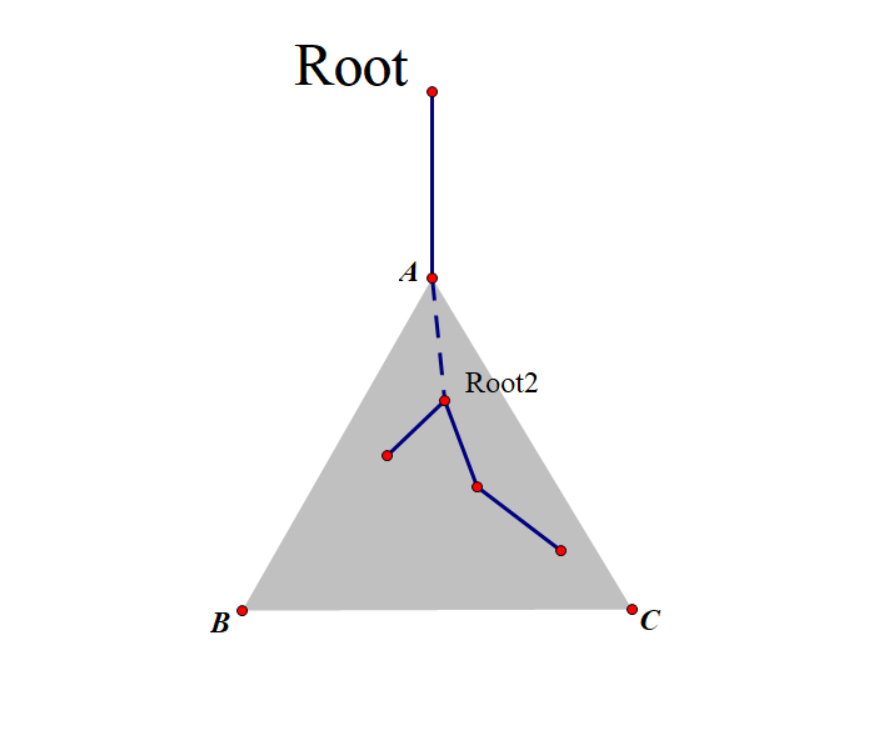
Root为根的子树中存在答案(下方路径),可以看成以Root2为根的两棵子树存在答案。
此时情况1可以转化为情况2,说明可以使用分治的方法统计。这是点分治的基本原理。
选根(选重心为根)
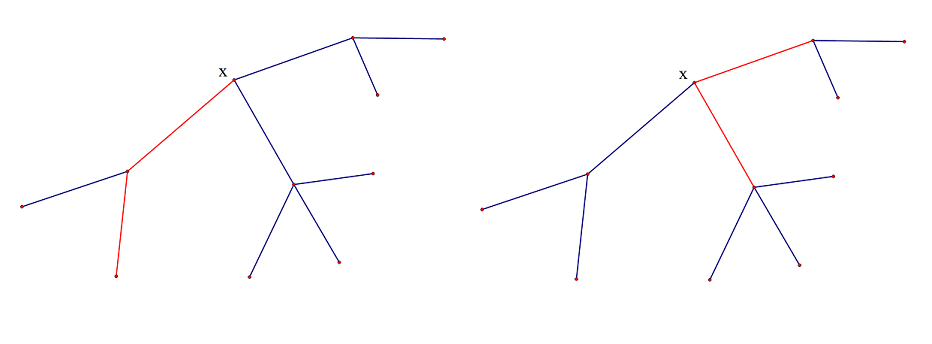
选根不同会影响遍历的效率,下图中选x为根优于选y为根。
重心为根时,所有的子树的大小都不超过整个树大小的一半。
可以发现,找树的重心(最大的子树最小的根节点)是最优的。
树形dp求树的重心:
void GET_ROOT(int x,int fa){ f[x]=0,siz[x]=1; //f[i]表示此点为根的最大子树的大小 for(int i=head[x];i;i=e[i].nextt){ int y=e[i].ver; if(used[y]||y==fa) continue; GET_ROOT(y,x); //向下遍历 f[x]=max(f[x],siz[y]); siz[x]+=siz[y]; } f[x]=max(f[x],Siz-siz[x]);
//Siz表示【现在这棵子树中】点的总数,一开始求重心时Siz=n if(f[x]<f[rt]) rt=x; //更新root }
之后的分治过程还需要对子树单独找重心,所以代码中有used[ ],一开始无影响。
求距离(枚举+子树容斥)
找到重心作为根之后,求出重心到子树中各个点的距离。
枚举子树里的两个点,如果两个点到重心的距离和为k,答案+1,这是第二种情况。
第一种情况就让距离根为k的点跟重心配对就行了,因为重心到重心的距离为0。
统计答案(二分+子树容斥)
考虑枚举一个点,另一个点可以通过二分来求解。
将距离进行排序,转化为找距离为 k -枚举点的距离 的点的个数。
因为距离已经排序过,所以可以二分出相同值的左右边界l、r,ans+=r-l+1。
int calc(int u,int d0){ //↑↑↑此时以u为根节点,统计子树中符合条件的点对个数 cnt=0; dep[u]=d0; getdeep(u,0); sort(o+1,o+cnt+1); //排序,便于二分 int l=1,r=cnt,res=0; while(l<r){ if(o[l]+o[r]<=k) res+=r-l,l++; else r--; //二分求符合条件的点对个数 } return res; }
【poj 1741】Tree
- n个点的树,每条边都有一个权值。
- 两点路径长度就是路径上各边权值之和。
- 求长度不超过K的路径有几条。
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N=50019; struct edge{ int ver,nextt,w; }e[N<<1]; //边集 int n,m,k,head[N],cnt; //head[]和cnt是边集数组的辅助变量 int root,sum; //当前查询的根,当前递归的这棵树的大小 int vis[N]; //某一个点是否被当做根过 int sz[N]; //每个点下面子树的大小 int f[N]; //每个点为根时,最大子树大小 int dep[N]; //每个点的深度(此时是与根节点的距离) int o[N]; //每个点的深度(用于排序,进而用于二分) int ans; //最终统计的答案 int reads(){ //读入优化 int x=0,w=1; char ch=getchar(); while((ch<'0'||ch>'9')&&ch!='-') ch=getchar(); if(ch=='-') w=0,ch=getchar(); while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar(); return w?x:-x; } void getroot(int u,int fa){ //dfs求重心和子树大小 sz[u]=1; f[u]=0; for(int i=head[u];i;i=e[i].nextt){ int v=e[i].ver; if(v==fa||vis[v]) continue; getroot(v,u); sz[u]+=sz[v]; f[u]=max(f[u],sz[v]); } f[u]=max(f[u],sum-sz[u]); //注意:可能是另外一半的树 if(f[u]<f[root]) root=u; //更新重心 } void getdeep(int u,int fa){ //dfs求出与根节点的距离 o[++cnt]=dep[u]; //用于排序 for(int i=head[u];i;i=e[i].nextt){ int v=e[i].ver; if(v==fa||vis[v]) continue; dep[v]=dep[u]+e[i].w; getdeep(v,u); } } int calc(int u,int d0){ //↑↑↑此时以u为根节点,统计子树中符合条件的点对个数 cnt=0; dep[u]=d0; getdeep(u,0); sort(o+1,o+cnt+1); //排序,便于二分 int l=1,r=cnt,res=0; while(l<r){ if(o[l]+o[r]<=k) res+=r-l,l++; else r--; //二分求符合条件的点对个数 } return res; } void solve(int u){ ans+=calc(u,0); vis[u]=1; //↑↑会产生非法路径(被u的某个子树完全包含,路径不能合并) for(int i=head[u];i;i=e[i].nextt){ //递归子树 int v=e[i].ver; if(vis[v]) continue; ans-=calc(v,e[i].w); //容斥原理去除非法答案 //↑↑在处理子树时,将初始长度设为连接边长e[i].w; //这样做就相当于给子树的每个组合都加上了u—>的路径。 sum=sz[v]; root=0; //重设当前总树大小,寻找新的分治点 getroot(v,0); solve(root); //递归新的分治点(重心) } } int main(){ n=reads(); int u,v,w; for(int i=1;i<n;i++){ u=reads(); v=reads(); w=reads(); //↓前向星 e[++cnt]=(edge){v,head[u],w}; head[u]=cnt; e[++cnt]=(edge){u,head[v],w}; head[v]=cnt; } root=0; sum=f[0]=n; //一开始,root初始化为0,用于找重心 k=reads(); getroot(1,0); solve(root); //从重心开始点分治 printf("%d\n",ans); return 0; }


