【暖*墟】 #AC自动机# AC自动机的总结与运用

 

KMP：匹配单串，线性扫描，在失配时用next数组引导j指针回溯，进行下一步匹配。

Trie树：多模式的匹配，构造26叉树，同时记录多个串的情况，记录结尾，进行匹配。

    KMP + Trie树 = AC自动机 　　

AC自动机：给一个字典，再给一个文本，问这个文本里出现了字典里的哪些字。

可以用n个单词的n次KMP算法来做 O(n*m*单词平均长度)，

也可以用1个Trie树去匹配文本串的每个字母位置来做 O(m*每次字典树遍历的平均深度)。

在AC自动机中，我们首先将每个模式串插入到Trie树中，建立一棵Trie树，

然后构建 fail指针（匹配失败时用来引导p指针回溯，插穿在Trie树的各个节点之间的指针）。

类似KMP算法中的next数组，能在失配时跳转到【具有最长公共前后缀】的字符继续匹配。

如果跳转，跳转后的串的前缀 必为 跳转前的模式串的后缀（向上跳），

并且跳转的新位置的深度（匹配字符个数）一定小于跳之前的节点。

 

一、AC自动机的构建步骤

 

1.将所有模式串构建成 Trie 树。

2.对 Trie 上所有节点构建前缀指针（类似kmp中的next数组）

3.利用前缀指针对主串进行匹配。

 

• AC自动机关键点一：trie字典树的构建过程

字典树的构建过程是这样的，当要插入许多单词的时候，我们要从前往后遍历整个字符串，

当我们发现当前要插入的字符其节点再先前已经建成，我们直接去考虑下一个字符即可，

当我们发现当前要插入的字符没有再其前一个字符所形成的树下没有自己的节点，

我们就要创建一个新节点来表示这个字符，接下往下遍历其他的字符。然后重复上述操作。

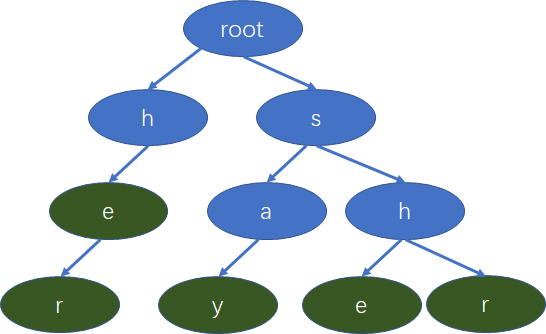
假设我们有下面的单词，she , he ,say, her, shr ,我们要构建一棵字典树。

​

 

 

• AC自动机关键点二：找Fail指针

在KMP算法中，当我们比较到一个字符发现失配的时候我们会通过next数组，

找到下一个开始匹配的位置，然后进行字符串匹配，当然KMP算法试用于单模式匹配。

所谓单模式匹配，就是给出一个模式串，给出一个文本串，寻找是否包含模式串。

AC自动机中，有fail指针，当发现失配的字符失配的时候，跳转到fail指针指向的位置，

然后再次进行匹配操作，AC自动机之所以能实现多模式匹配，就归功于fail指针的建立。

当前节点t有fail指针，其fail指针所指向的节点和t所代表的字符是相同的。

因为t匹配成功后，我们需要去匹配 t->child，发现失配，那么就从t->fail开始再次匹配。

Fail指针的求法：BFS。直接与根节点相连的节点失配，他们的fail指针直接指向root。

其他节点的fail指针：假设当前节点为father，其孩子节点记为child。

求child的Fail指针时，首先我们要找到其father的Fail指针所指向的节点t，

看t的孩子中有没有和child节点所表示的字母相同的节点，如果有、就是child的fail指针；

如果没有，找father->fail->fail，重复过程，直到到达root（指向root）。

 

• AC自动机关键点三：文本串的匹配

(1)当前字符匹配，表示从当前节点沿着树边有一条路径可以到达目标字符，

如果当前匹配的字符是一个单词的结尾，我们可以沿着当前字符的fail指针，一直遍历到根，

如果这些节点末尾有标记（标记代表节点是一个单词末尾），遍历到的都是可以匹配上的节点。

统计完毕后标记。此时沿该路径走向下一个节点继续匹配，目标指针移向下个字符。

 

(2)当前字符不匹配，则去当前节点fail指针所指向的字符继续匹配，直到指针指向root。

 

重复这2个过程中的任意一个，直到文本串走到结尾为止。

 

​

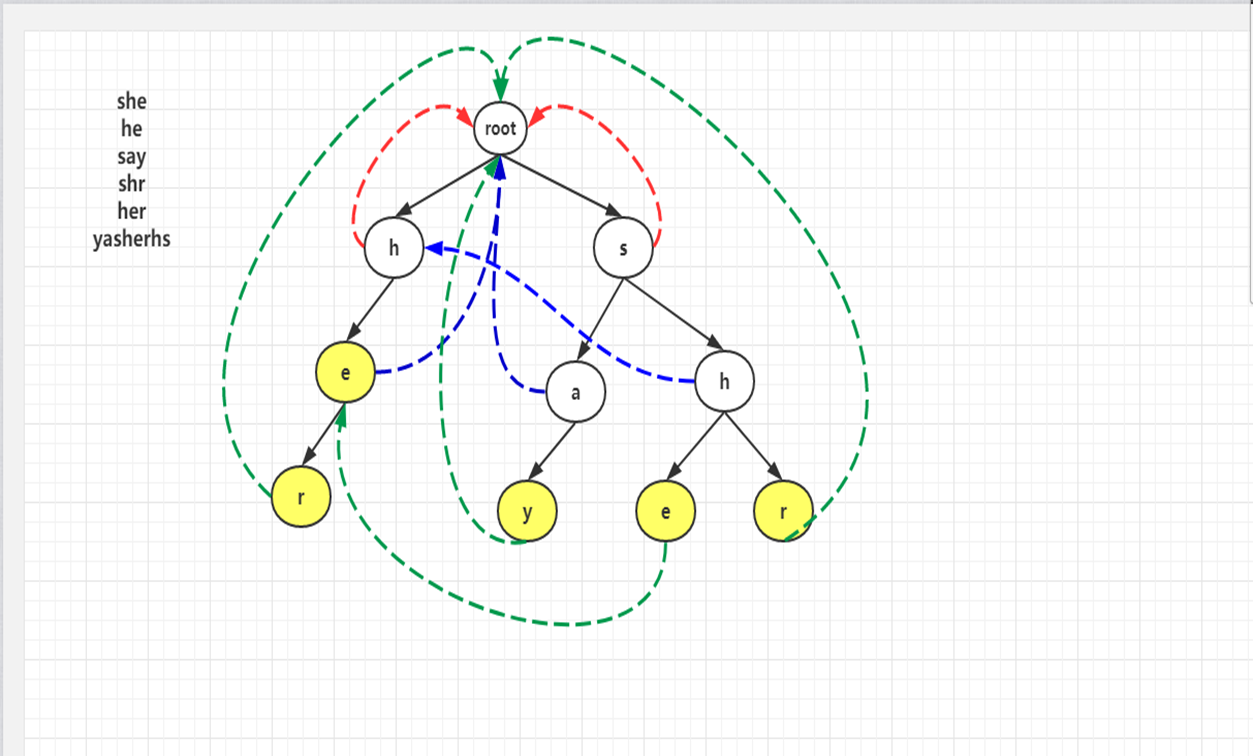
对照上图，看一下模式匹配这个详细的流程，其中文本串为 yasherhs（某文章）。

对于i=0,1，Trie 中没有对应的路径，故不做任何操作；

i=2,3,4时，指针p走到左下节点e。因为节点e的 count 信息为1，所以cnt+1，

（到达某一个单词的末尾，该信息用bool tail [ ] 记录，单词数++）。

并且将节点e的 count 值设置为-1，表示该单词已经出现过了，防止重复计数。

最后 temp 指向e节点的失败指针所指向的节点继续查找。

以此类推，最后 temp 指向 root，退出 while 循环，这个过程中 count 增加了2。

表示找到了2个单词she和he。当i=5时，程序进入第5行，p指向其失败指针的节点，

也就是右边那个e节点，随后在第6行指向r节点，r节点的 count 值为1，

从而count+1，循环直到 temp 指向 root 为止。最后i=6,7时，找不到任何匹配，结束。

 

二、代码实现

• 构建Trie树：

//trie字典树：
int tot=1,trie[maxn][26];
bool tail[maxn]; //串尾元素标记
void make_trie(char* s){ //insert
    int len=strlen(s),p=1; //p从根节点开始
    for(int i=0;i<len;i++){
        int ch=s[i]-'A'; //按照具体情况转为数字
        if(!trie[p][ch]) trie[p][ch]=++tot; //tot用于节点编号
        p=trie[p][ch];
    } tail[p]=true; //标记串尾元素
}

 

• fail指针的实现：（名称用nextt数组代替）

//fail指针：（名称可以用nextt数组代替）

int nextt[maxn],que[maxn];

void bfs(){
    for(int i=0;i<26;i++) trie[0][i]=1; 
    //↑↑↑初始化：0的所有转移边都设为根节点为1
    que[1]=1; nextt[1]=0; //que为广搜队列
    for(int q1=1,q2=1;q1<=q2;q1++){ //q1,q2相当于head,tail
        int p=que[q1]; //队列中head位置对应的节点编号
        for(int i=0;i<26;i++){ //遍历该编号能对应的所有字母
            if(!trie[p][i]) trie[p][i]=trie[nextt[p]][i];
            //↑↑↑若不存在trie[p][i]，则沿p的前缀指针走到第一个满足存在的字符i转移边
            //则会得到结点v=nextt[p]，对应值就是trie[nextt[p]][i]
            else que[++q2]=trie[p][i], //trie[p][i]存在，存入队尾
                nextt[trie[p][i]]=trie[nextt[p]][i]; //记录fail指针
            }
        }
    }
}

 

• 文本串的匹配：

//匹配是否存在：
int find1(){ int p=1;
    for(int i=1;i<=m;i++){
        p=trie[p][a[i]]; //向下层寻找匹配字符
        if(tail[p]) return false; //匹配到返回0，否则返回1
    } return true;
}

//文章匹配单词数：
void find2(char *s){
    int p=1,len=strlen(s),c,k;
    for(int i=0;i<len;i++){
        c=s[i]-'a'; k=trie[p][c];//p为层数（节点编号）
        while(k>1){ //可以匹配的到 && 不是根节点
            ans+=tail[k]; //如果到达一处单词结尾，ans+=1
            tail[k]=0; //防止重复计数
            k=nextt[k]; //返回上层的该元素出现位置，重新找
        }
        p=trie[p][c]; //向下层寻找匹配字符编号
    }
}

 

 

 

 

 

                                  ——时间划过风的轨迹，那个少年，还在等你。