DP优化——动态dp&全局平衡二叉树
适用场景
动态 dp 主要用来处理动态修改点权/边权,的树形dp题 或者 区间序列上的带修改的dp。
其核心都是把 dp 变成矩乘的形式,这样修改只需要更改某个矩阵,再用线段树等数据结构维护。
以板子题为例进行讲解。
【模板】"动态 DP"&动态树分治
这道题是简单版。
简单版的前置知识:树链剖分,广义矩阵乘法。
不带修改的话,最大权独立集很简单:
\(f[u][0] = \sum _{v\in son(u)}\max(f[v][0],f[v][1])\),表示不选 \(u\) 的答案。
\(f[u][1] = w[u] + \sum _{v\in son(u)}f[v][0]\),表示选 \(u\) 的答案。
注意到我们更改一个点的点权其实只会修改他到根的链上的那些 dp 值,所以全部重算一点都不划算。
考虑只去更改这条链上的 dp 值。
但这样当树是链时还是有可能 TLE (虽然题解区似乎有人 \(n\) 方过百万),这个时候就会想到树链剖分。
因为根到一个点最多会有 \(\log\) 个不同的重链,所以可以考虑重链之间暴力修改,重链上用线段树快速维护。
这样的话我们就需要更改一下 \(f\) 的转移,使得能与树剖的性质匹配(\(f\) 的定义不变)。
设 \(g[u][0/1]\) 表述 \(u\) 选/不选,只考虑 \(u\) 的那些轻儿子,的答案。
那么(\(son[u]\) 表示 \(u\) 的重儿子):
\(f[u][0] = g[u][0] + \max(f[son[u][0],f[son[u][1])\)
\(f[u][1] = g[u][1] + f[son[u]][0]\)。
特别的,叶子结点的 \(g[u][0]=0,g[u][1]=w[u]\) (和他的 \(f\) 相同)。
没了讨厌的 \(\sum\),加上为了便于用线段树维护,这个转移我们尝试改写成矩阵。
\(f[u][0] = \max(g[u][0]+f[son[u][0] , g[u][0]+f[son[u]][1])\)
\(f[u][1] = g[u][1] + f[son[u]][0]\)
根据这个可以得到他的 \((+,\max)\) 广义矩阵乘法形式。
会得到转移矩阵里只跟当前点的 \(g\) 有关。
注意到转移时我们只需要重儿子的信息,以及当前点的 \(g\) 值,所以我们在线段树上维护每个点的 \(g\) 所构成的转移矩阵以及矩阵的区间乘积。
又注意到一条重链的底部一定是叶子。
所以对于一条重链的顶端他的 \(f\) 值就是这条重链的每个转移矩阵的乘积再乘一个初始矩阵(就是叶子的 \(f\) 值),这个区间乘线段树是好维护的。
所以我们只维护 \(g\) (或者其实是转移矩阵)就可以了。
修改流程如下:
- 当修改一个点 \(u\) 的点权时,当前点的 \(g[u][1]\) 要变一下。
- 然后 \(u\) 到重链顶端 \(top[u]\) 的所有点的 \(g\) 都是不变的,因为 \(g\) 在计算时不包含重儿子。
- 当 \(top[u]\) 跳到 \(fa[top[u]]\) 时,这时因为 \(top[u]\) 是 \(fa[top[u]]\) 的轻儿子,所以要更改 \(fa[top[u]]\) 的 \(g\) 值。
算 \(fa[top[u]\) 的 \(g\) 值要用到 \(top[u]\) 的 \(f\) 值,所以这个时候需要在线段树上区间查询一下。
复杂度是 \(O(n \log^2n)\),因为修改时要跳 \(\log\) 次,每跳一次都要在线段树上查询一次。
一些细节:
矩阵乘法不满足交换律,所以线段树上 pushup 要从后往前合并。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,T,w[N];
int tot,head[N],to[N<<1],Next[N<<1];
void add(int u,int v){
to[++tot]=v,Next[tot]=head[u],head[u]=tot;
}
int top[N],down[N],rev[N],dfn[N],fa[N],son[N],Size[N],num,g[N][2],f[N][2];
//down是重链底端
void dfs1(int u){
Size[u]=1;
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(v==fa[u]) continue;
fa[v]=u;
dfs1(v);
Size[u]+=Size[v];
if(Size[v]>Size[son[u]]) son[u]=v;
}
}
void dfs2(int u){
dfn[u]=++num;
rev[num]=u;
if(son[fa[u]]==u) top[u]=top[fa[u]];
else top[u]=u;
if(son[u]) dfs2(son[u]),down[u]=down[son[u]];
else down[u]=u;
g[u][1]=w[u];
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(v==fa[u]||v==son[u]) continue;
dfs2(v);
g[u][0]+=max(f[v][0],f[v][1]);
g[u][1]+=f[v][0];
}
f[u][0]=g[u][0]+max(f[son[u]][0],f[son[u]][1]);
f[u][1]=g[u][1]+f[son[u]][0];
}
struct Matrix{
int n,m,a[3][3];
void Init(){memset(a,-0x3f,sizeof a);}
void Init2(){ //单位矩阵
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(i==j) a[i][j]=0;
else a[i][j]=-0x3f3f3f3f;
}
}
}
}F;
Matrix operator *(Matrix A,Matrix B){
Matrix C; C.Init();
C.n=A.n,C.m=B.m;
for(int i=1;i<=C.n;i++){
for(int j=1;j<=C.m;j++){
for(int k=1;k<=A.m;k++){
C.a[i][j]=max(C.a[i][j],A.a[i][k]+B.a[k][j]);
}
}
}
return C;
}
struct node{
int l,r;
Matrix G;
};
struct SegmentTree{
node t[N<<2];
void pushup(int p){
t[p].G=t[p<<1|1].G*t[p<<1].G;
}
void build(int p,int l,int r){
t[p].l=l,t[p].r=r;
if(l==r){
t[p].G.n=2,t[p].G.m=2;
int u=rev[l];
t[p].G.a[1][1]=g[u][0],t[p].G.a[1][2]=g[u][1],t[p].G.a[2][1]=g[u][0],t[p].G.a[2][2]=-0x3f3f3f3f;
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
pushup(p);
}
void change(int p,int x){
if(t[p].l==t[p].r){
int u=rev[x];
t[p].G.a[1][1]=g[u][0],t[p].G.a[1][2]=g[u][1],t[p].G.a[2][1]=g[u][0],t[p].G.a[2][2]=-0x3f3f3f3f;
return;
}
int mid=(t[p].l+t[p].r)>>1;
if(x<=mid) change(p<<1,x);
else change(p<<1|1,x);
pushup(p);
}
Matrix ask(int p,int l,int r){
if(l<=t[p].l&&t[p].r<=r) return t[p].G;
int mid=(t[p].l+t[p].r)>>1;
Matrix Res; Res.n=2,Res.m=2,Res.Init2();
if(r>mid) Res=Res*ask(p<<1|1,l,r);
if(l<=mid) Res=Res*ask(p<<1,l,r);
return Res;
}
}Seg;
void Init(){ //预处理:树剖,g 数组,f 数组,初始化线段树
dfs1(1);
dfs2(1);
Seg.build(1,1,n);
F.n=1,F.m=2;
F.a[1][1]=0,F.a[1][2]=-0x3f3f3f3f; //初始矩阵,F 乘以叶子的转移矩阵就是叶子的 f。
}
void change(int x,int y){
int tmp=x;
x=top[x];
while(x!=1){ //先算出涉及到的点原来的 f
Matrix Ans=F;
Ans=Ans * Seg.ask(1,dfn[x],dfn[down[x]]);
f[x][0]=Ans.a[1][1],f[x][1]=Ans.a[1][2];
g[ fa[x] ][0] -= max(f[x][0],f[x][1]);
g[ fa[x] ][1] -= f[x][0];
x=top[fa[x]];
}
x=tmp;
g[x][1]-=w[x] , w[x]=y , g[x][1]+=w[x];
Seg.change(1,dfn[x]);
x=top[x];
while(x!=1){
Matrix Ans=F;
Ans=Ans * Seg.ask(1,dfn[x],dfn[down[x]]);
f[x][0]=Ans.a[1][1],f[x][1]=Ans.a[1][2];
g[ fa[x] ][0] += max(f[x][0],f[x][1]);
g[ fa[x] ][1] += f[x][0];
Seg.change(1,dfn[fa[x]]);
x=top[fa[x]];
}
}
signed main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n=read(),T=read();
for(int i=1;i<=n;i++) w[i]=read();
for(int i=1;i<n;i++){
int u=read(),v=read();
add(u,v),add(v,u);
}
Init();
while(T--){
int x=read(),y=read();
change(x,y);
Matrix Ans=F;
Ans=Ans * Seg.ask(1,dfn[1],dfn[down[1]]);
printf("%d\n",max(Ans.a[1][1],Ans.a[1][2]));
}
return 0;
}
注意到树剖是 \(O(n \log^2n)\) 虽然常数小但还是容易被卡,而什么 LCT 虽然是 \(O(n \log n)\) 但是常数巨大还不如两个 \(\log\),于是毒瘤聪明的出题人就出了这题:
【模板】"动态DP"&动态树分治(加强版)
把树剖卡掉了。
那有什么别的办法呢?
于是就诞生了这个非常厉害的科技——全局平衡二叉树。
请确保先会了简单版的树剖 + 线段树写法。
思考树剖为什么需要两个 \(\log\),因为我们每往上跳一次就要做一次 \(O(\log n)\) 的区间查询,然后我们一共要跳 \(\log\) 次,所以是两个 \(\log\)。
考虑把一个 \(\log\) 去掉,跳 \(\log\) 次重链的这个 \(\log\) 肯定是去不掉了,只能去掉那个查询的 \(\log\)。
但是很难有一个数据结构能 \(O(1)\) 维护一个比较复杂的且带修的区间信息。
所以全局平衡二叉树的主要思路就是使树高直接变成 \(\log\),然后每一次真的直接往上一步步跳,而不是跳一条重链,在跳的过程中上传信息并合并(这个容易做到 \(O(1)\)),这样每次跳都是 \(O(1)\) 的了。
怎么建树呢?
- 首先全局平衡二叉树先对每条重链建了一个平衡二叉树,每条重链的建法是:
- 先一遍 dfs 维护出基本信息 \(Size\) 表示子树大小,\(son\) 表示重儿子,\(lsiz\) 表示除去重儿子所在子树的子树大小。
- 然后对每条重链弄一个类似点分治的过程,把这条链搞到一段序列上,每次找出以 \(lsiz\) 为权值的带权中点 \(rt\);
以 \(rt\) 为平衡二叉树的根,然后左右分别递归建树并把左右两边得到的根设为 \(rt\) 的左右儿子。
- 然后把一个点用轻边连接的儿子对应的平衡二叉树的根接到这个点对应的平衡二叉树的根下面。
举个例子,比如这个图:
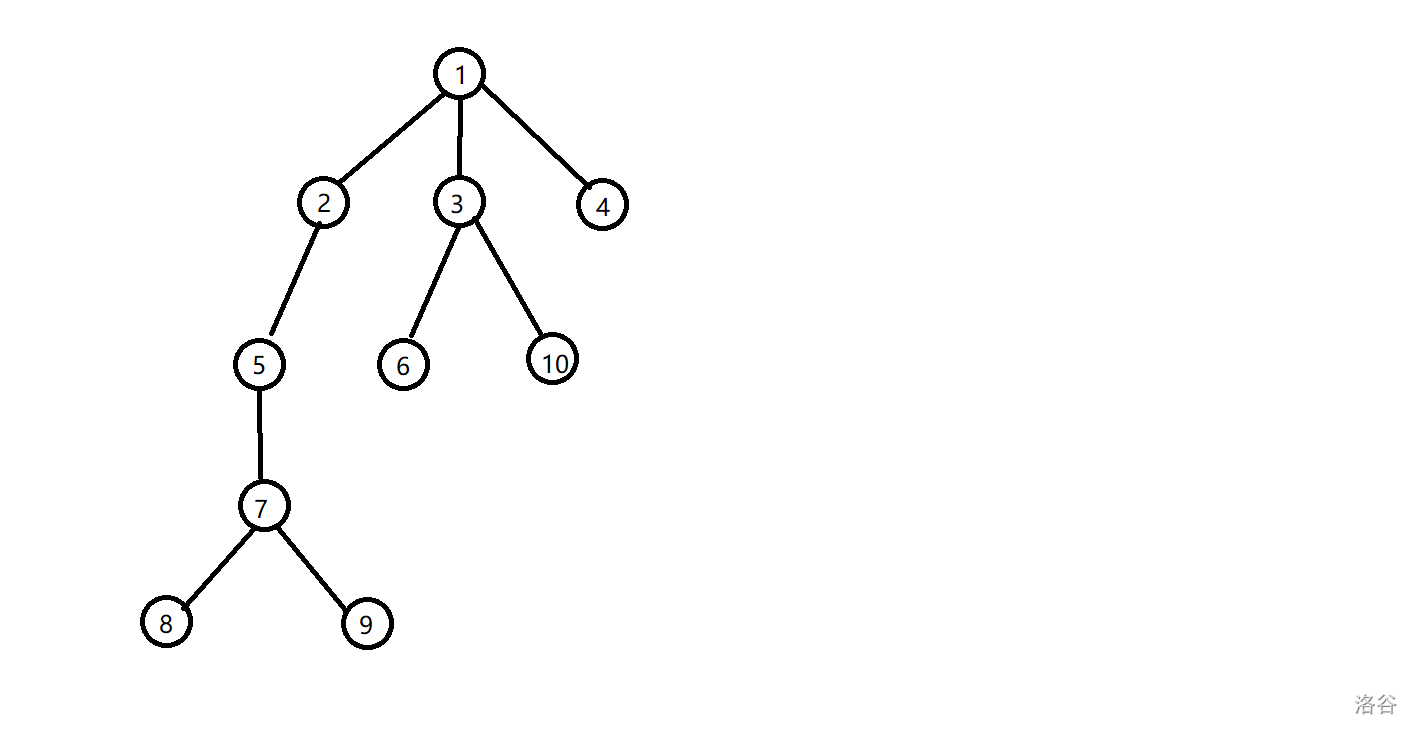
他的重链以及 \(lsiz\) 如下图所示:
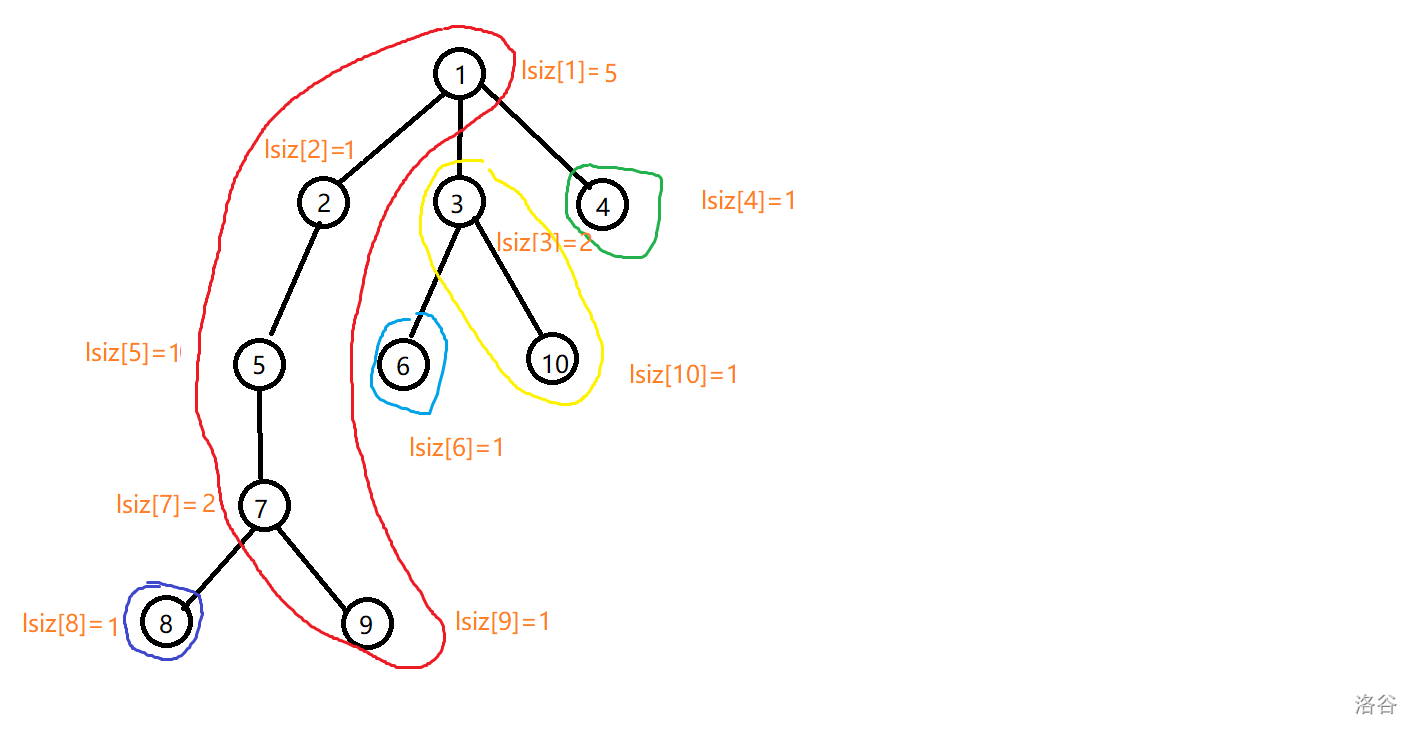
那么他建出的全局平衡二叉树应该长这样子,不同颜色代表不同重链建出的平衡二叉树,虚线边代表连接这些二叉树的边:

Tip:所以可以看出全局平衡二叉树并不是一棵二叉树,而是一个二叉树森林连接起来得到的一棵多叉树。
思路就是这么个思路,代码实现时:
递归建树,当 build 到一个点 \(u\) 时,先拉出重链,
然后对重链上的每个点先去递归它的轻儿子并把返回的根接到那个点上(对于轻边我们只记录父亲而不记录儿子)。
对于一条重链再按照上面所说的方法去特殊地建树,
并维护出这个重链的所有转移矩阵的乘积,只要每次 pushup 即可,还是记得注意顺序,因为矩阵乘法没有交换律。
到此全局平衡二叉树就建完了。
全局平衡二叉树的每个点维护了两个信息,自己这个点本身的转移矩阵 \(matr1\),他所代表的重链上的区间的转移矩阵的乘积 \(matr2\)。
修改时,我们从修改的点开始,先改掉它对应的转移矩阵 \(matr1\) (此时先不要 pushup 更改自身的 \(matr2\),因为后面需要用到旧的 \(matr2\))。
然后在全局平衡二叉树上一步一步往上跳,假设当前在 \(u\) 点,全局平衡二叉树上的父亲为 \(fa\):
- 如果 \((u,fa)\) 这条边是重边就直接
pushup(u)把 \(u\) 的 \(matr2\) 改掉,先不用修改 \(fa\) 的 \(matr2\); - 如果 \((u,fa)\) 这条边是轻边,此时 \(u\) 的 \(matr2\) 是旧版本,可以很快的求出 \(u\) 原先的 \(f\) 值,把 \(fa\) 的转移矩阵 \(matr1\) 减掉旧的 \(f\) 值;再
pushup(u),算出新的 \(f\) 值,把 \(fa\) 的转移矩阵 \(matr1\) 加上新的 \(f\) 值。
查询时,如果查询根的话,直接查询根所在重链的转移矩阵的乘积即可。
查询子树的话,我们需要的是原树上查询点 \(u\) 到其所在重链底端的所有矩阵的乘积,从全局平衡二叉树的 \(u\) 点开始,下面 \(treefa[u]\) 表示 \(u\) 在全局平衡二叉树上的父亲。
- 把自身节点的 \(matr1\) 以及右儿子的 \(matr2\) 统计入答案。
- 如果 \(u\) 是父亲 \(treefa[u]\) 的左儿子,那么需要把父亲的 \(matr1\) 以及父亲的右儿子的 \(matr2\) 统计上;否则这一步不进行操作。
- 跳到父亲。
- 重复执行 2~3 步直到跳到根。
比如有一条有 \(12\) 个点的重链,它们对应到区间上长这样:

把他特殊建出的平衡二叉树长这样(圈出的点是每一层的根,只圈出了需要用到的根):
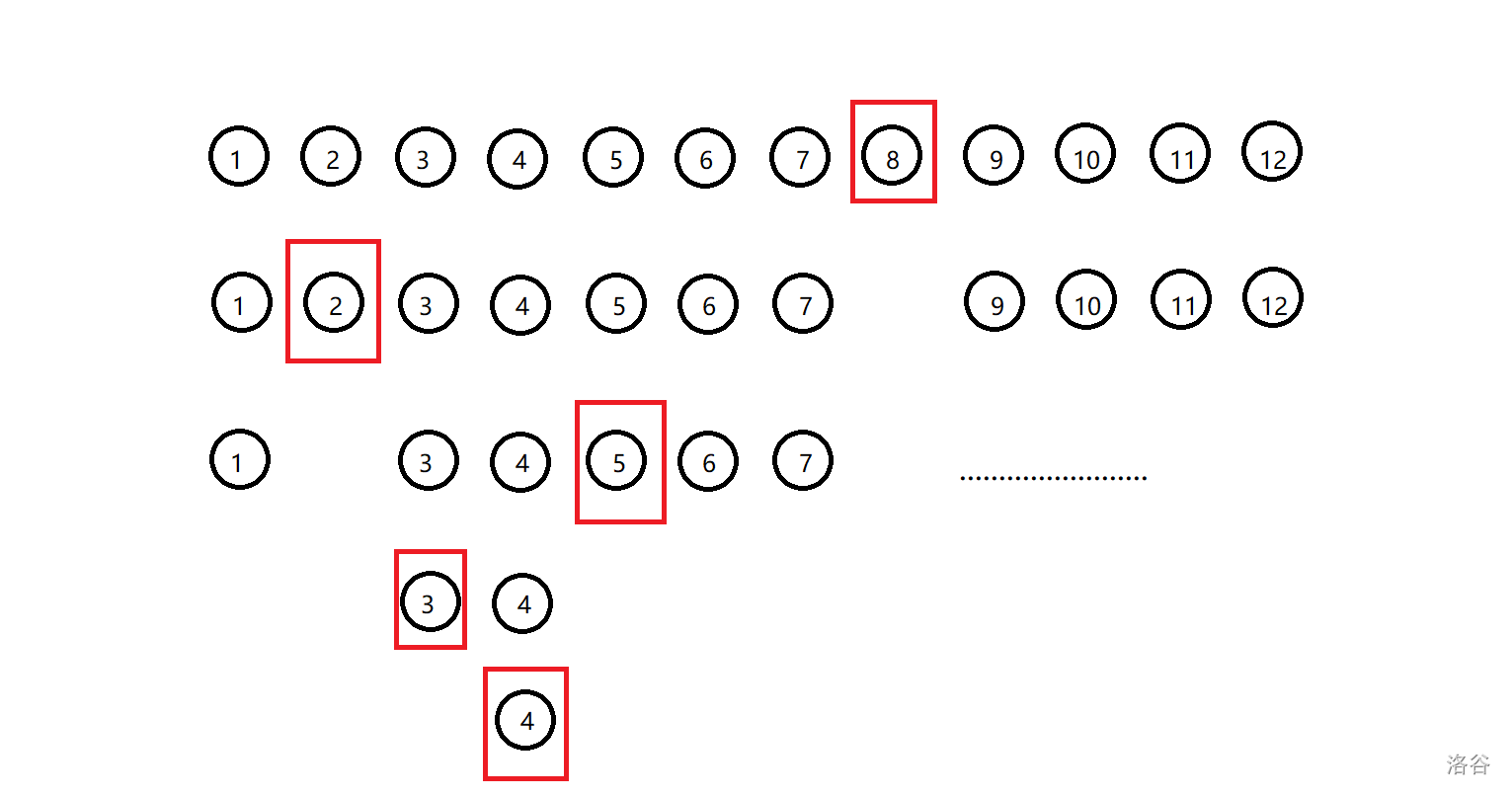
现在要查询 \(4\) 号点子树内的信息,就是查询区间 \([4,12]\) 内的点的转移矩阵的乘积。模拟上述过程如下:
- 将 \(4\) 号点自身的转移矩阵和右子树代表的区间(这个图里没有)的转移矩阵的乘积计入答案。
此时计入答案的点:\(4\)。 - 因为 \(4\) 号点是 \(3\) 号点的右儿子所以 \(3\) 号点不计入答案,然后跳到 \(3\) 号点。
此时计入答案的点:\(4\)。 - \(3\) 号点是 \(5\) 号点的左儿子,所以 \(5\) 号点以及 \(5\) 号点的右子树代表的区间 \([6,7]\) 计入答案,并跳到 \(5\) 号点。
此时计入答案的点:\(4,5,6,7\)。 - \(5\) 号点是 \(2\) 号点的右儿子,不操作,并跳到 \(2\) 号点。
此时计入答案的点:\(4,5,6,7\)。 - \(2\) 号点是 \(8\) 号点的左儿子,将 \(8\) 号点,以及右子树区间 \([9,12]\) 计入答案。并跳到 \(8\) 号点。
此时计入答案的点:\(4,5,6,7,8,9,10,11,12\)。 - 跳到根了,结束。
查询子树的复杂度为 \(O(\log n)\)。
时间复杂度分析:
- 如果往下的边是轻边,每一次子树大小减少一半,所以至多走 \(O(\log n)\) 条轻边;
- 如果往下的边是重边,因为重边特殊的建法,每一次取带权中点,子树大小也减半,所以至多走 \(O(\log n)\) 条重边。
所以树高是 \(O(\log n)\) 的。
一些细节见代码,个人认为码量和树剖差不多。
code
#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=1e6+5,inf=0x3f3f3f3f;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,T,w[N];
int tot,head[N],to[N<<1],Next[N<<1];
void add(int u,int v){
to[++tot]=v,Next[tot]=head[u],head[u]=tot;
}
int son[N],Size[N],lsiz[N],g[N][2],f[N][2];
void dfs1(int u,int fa){
Size[u]=1;
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(v==fa) continue;
dfs1(v,u);
Size[u]+=Size[v];
if(Size[v]>Size[son[u]]) son[u]=v;
}
lsiz[u]=Size[u]-Size[son[u]];
}
void dfs2(int u,int fa){
if(son[u]) dfs2(son[u],u);
g[u][1]=w[u];
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(v==fa||v==son[u]) continue;
dfs2(v,u);
g[u][0]+=max(f[v][0],f[v][1]);
g[u][1]+=f[v][0];
}
f[u][0]=g[u][0]+max(f[son[u]][0],f[son[u]][1]);
f[u][1]=g[u][1]+f[son[u]][0];
}
struct Matrix{
int n,m,a[2][2];
void Init(){memset(a,-0x3f,sizeof a);}
}F;
Matrix operator *(Matrix A,Matrix B){
Matrix C; C.Init();
C.n=A.n,C.m=B.m;
for(int i=0;i<=C.n;i++){
for(int j=0;j<=C.m;j++){
for(int k=0;k<=A.m;k++){
C.a[i][j]=max(C.a[i][j],A.a[i][k]+B.a[k][j]);
}
}
}
return C;
}
struct Tree{
int ls,rs;
Matrix matr1,matr2;
}t[N];
void pushup(int p){
t[p].matr2=t[p].matr1;
//还是注意要从右往左合并,因为这个调了一个上午。
if(t[p].rs) t[p].matr2 = t[ t[p].rs ].matr2 * t[p].matr2;
if(t[p].ls) t[p].matr2 = t[p].matr2 * t[ t[p].ls ].matr2; //注意顺序
}
PII Getf(int p){ //得到此时 p 点的 matr2*F 的值(注意这个不一定是 p 点在原树上的 f 值,因为 matr2 不一定是原树上 p 到重链底端的所有转移矩阵的乘积)
Matrix Ans=F*t[p].matr2;
return {Ans.a[0][0],Ans.a[0][1]};
}
int treefa[N],root;
bool vis[N];
int st[N],top;
int SBuild(int l,int r){ //对重链特殊建树
if(l>r) return 0;
int sum=0;
for(int i=l;i<=r;i++) sum+=lsiz[st[i]];
for(int i=l,s=lsiz[st[l]];i<=r;i++,s+=lsiz[st[i]]){
if(s * 2 >= sum){ //带权中点
int p=st[i],lson=SBuild(l,i-1),rson=SBuild(i+1,r);
t[p].ls=lson,t[p].rs=rson;
treefa[lson]=treefa[rson]=p;
pushup(p);
return p;
}
}
return 0;
}
int Build(int u){
for(int x=u;x;x=son[x]) vis[x]=true;
for(int x=u;x;x=son[x]){
for(int i=head[x];i;i=Next[i]){ //先递归轻儿子
int y=to[i];
if(vis[y]) continue;
treefa[Build(y)]=x;
}
}
top=0; //因为 top 是全局变量,所以不能写在vis那里,不然在上面递归到 y 时就被覆盖了!!!
for(int x=u;x;x=son[x]) st[++top]=x;
return SBuild(1,top);
}
void Init(){ //预处理除了建树都和树剖写法一样
dfs1(1,0);
dfs2(1,0);
for(int x=1;x<=n;x++){
t[x].matr1.n=1,t[x].matr1.m=1;
t[x].matr1.a[0][0]=g[x][0],t[x].matr1.a[0][1]=g[x][1];
t[x].matr1.a[1][0]=g[x][0],t[x].matr1.a[1][1]=-inf;
}
F.n=0,F.m=1;
F.a[0][0]=0,F.a[0][1]=-inf;
root=Build(1);
}
void change(int u,int val){
t[u].matr1.a[0][1]+=val-w[u];
w[u]=val;
for(;u;u=treefa[u]){ //这里不能写 for(;u!=root;u=treefa[u]) 因为这样的话根的 matr2 没有被 pushup 更新。
int fa=treefa[u];
if(fa && t[fa].ls !=u && t[fa].rs != u){ //轻边
PII oldf=Getf(u);
t[fa].matr1.a[0][0] -= max(oldf.fi , oldf.se) ;
t[fa].matr1.a[0][1] -= oldf.fi ;
t[fa].matr1.a[1][0] -= max(oldf.fi , oldf.se) ;
pushup(u);
PII newf=Getf(u);
t[fa].matr1.a[0][0] += max(newf.fi , newf.se) ;
t[fa].matr1.a[0][1] += newf.fi ;
t[fa].matr1.a[1][0] += max(newf.fi , newf.se) ;
}
else pushup(u);
}
}
signed main(){
// freopen("P4751_4.in","r",stdin);
// freopen(".out","w",stdout);
n=read(),T=read();
for(int i=1;i<=n;i++) w[i]=read();
for(int i=1;i<n;i++){
int u=read(),v=read();
add(u,v),add(v,u);
}
Init();
int lstans=0;
while(T--){
int x=read()^lstans,y=read();
change(x,y);
PII ans=Getf(root);
lstans = max(ans.fi,ans.se);
printf("%d\n",lstans);
}
return 0;
}
参考网址:动态DP之全局平衡二叉树


 浙公网安备 33010602011771号
浙公网安备 33010602011771号