扩展KMP (Z 函数)

一些约定：

• 字符串下标从 \(1\) 开始。
• \(s[1,i]\) 表示字符串 \(s\) 的第一个到第 \(i\) 个字符组成的字符串。

Z 函数

我们定义：

• \(z[i]\) 表示最大的 \(len\) 使得 \(B[1,len]=B[i,i+len-1]\)。其中 \(z[1]=m\)。

• \(Z-box\)：这是我们在求 \(z\) 数组时维护的一段区间，用两个变量 \(l,r\) 表示，它表示目前为止 \(B\) 中右端点最大的一个区间 \([l,r]\) 满足，\(B[l,r]=B[1,r-l+1]\)。

知道了一些定义我们就来看 \(z\) 数组怎么求。
假设我们已经得出 \(z[1]~z[i-1]\) 了要求 \(z[i]\)，且目前的 \(Z-box=[l,r]\)。

1. \(l \le i \le r\) (实际上如果 \(i \le r\) , \(i\) 一定满足 \(l \le i \le r\))：

设 \(r’\) 表示 \(r-l+1\)，则 \(B[1,r’]=B[l,r]\) (为了下面叙述方便，我们称 \(r’\) 为 \(r\) 的对应点)，图片中相同颜色代表这段区间相同。

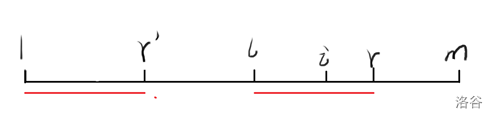
我们再求出 \(i\) 的对应点 \(i’=i-l+1\)，则 \(B[i’,r’]=B[i,r]\)。

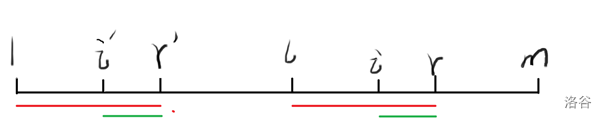
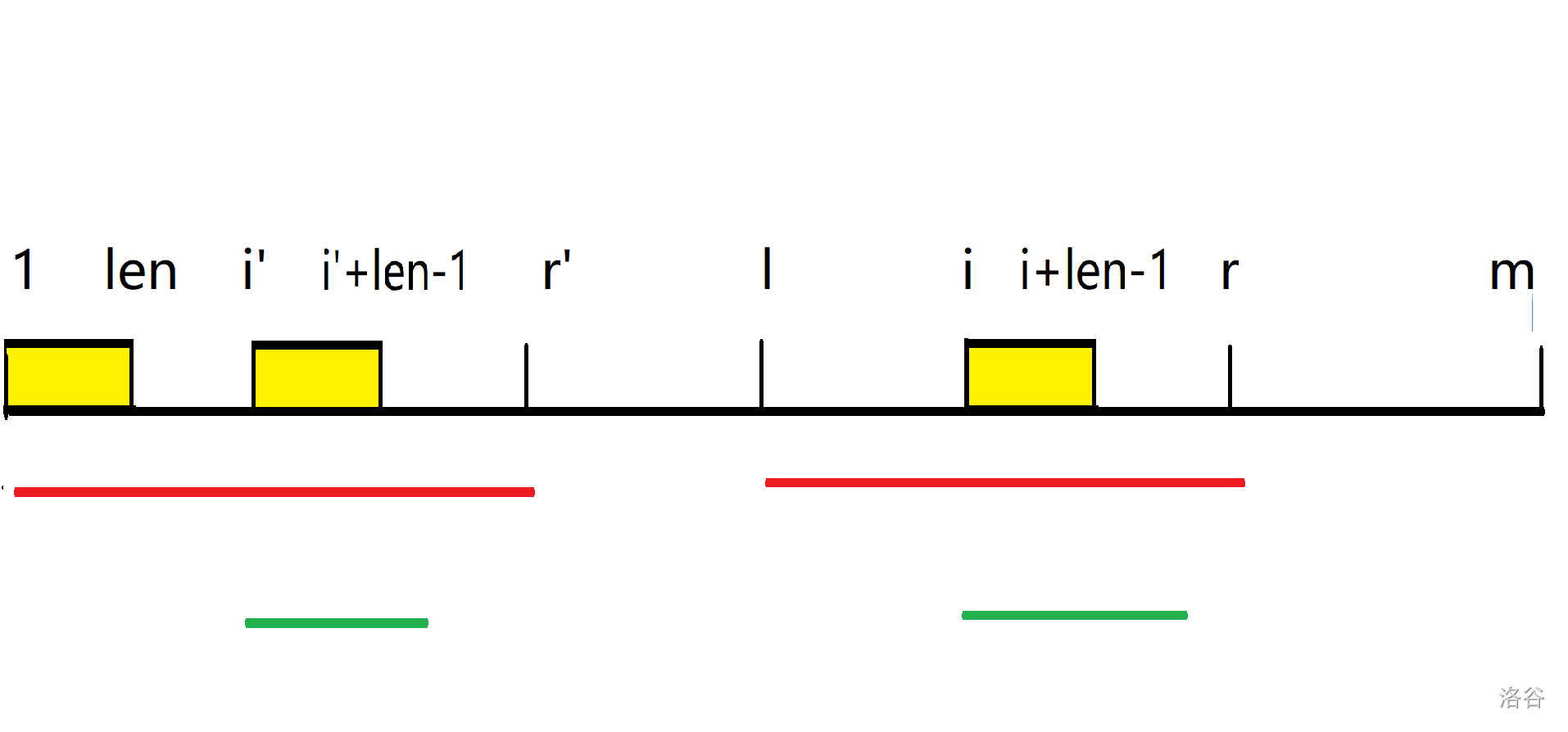
假设 \(z[i’]=len\) 则 \(B[1,len]=B[i’,i’+len-1]\)，现在又有两种情况：

• \(len \le r-i+1\)： 此时 \(B[1,len]=B[i’,i’+len-1]=B[i,i+len-1]\)，又因为 \(i+len-1\) 并未超过 \(Z-box\) 的右端点，所以必有 \(z[i]=len\)。

  

• 而如果 \(len>r-i+1\)，如下图

  

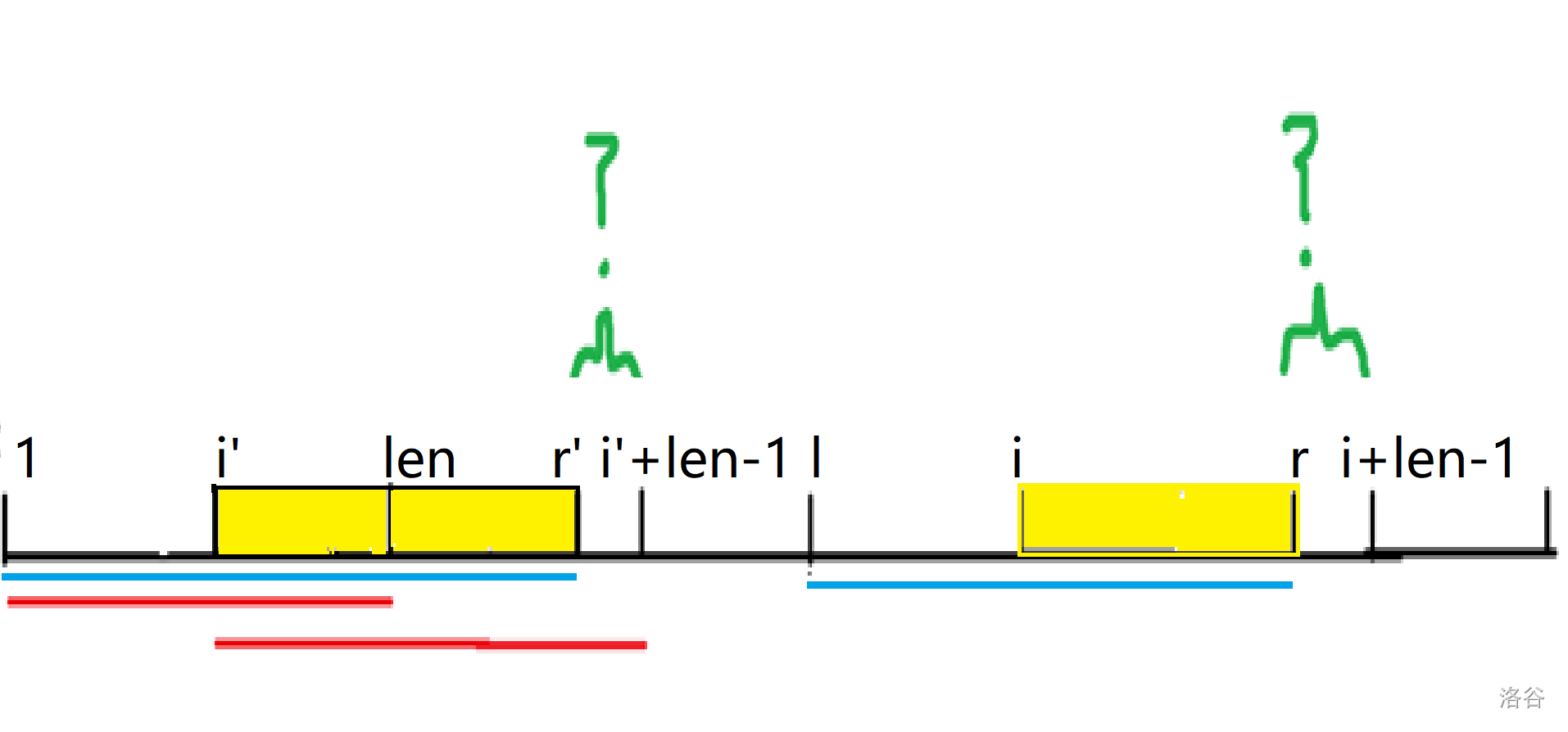
我们无法确定绿色部分是否相同，因此不能直接把 \(len\) 赋给 \(z[i]\)，但我们可以保证 \(z[i]\ge r-i+1\)，\(r\) 后面的部分我们暴力扫描判断。

2. \(i>r\)： 同样也是暴力往后扫描即可。

每次求完 \(z[i]\) 后如果 \(i+z[i]-1>r\) 则用 \(i\) 和 \(i+z[i]-1\) 更新 \(l,r\)。

求 \(z\) 数组的代码如下：

	z[1]=m,l=0,r=0;
	for(int i=2;i<=m;i++)
	{
		if(i<=r) z[i]=min(z[i-l+1],r-i+1);
		while(b[i+z[i]]==b[1+z[i]]) z[i]++; //如果i>r那这里z[i]一开始是0
		if(i+z[i]-1>r) r=i+z[i]-1,l=i; 
	}

复杂度分析： 会发现一旦出现暴力遍历的情况必然会更新右端点 \(r\)，而右端点只能更新 \(O(n)\) 次，再 \(r=n\) 之后就不会出现暴力扫描的情况了，因此复杂度是 \(O(n)\)。

P5410 【模板】扩展 KMP/exKMP（Z 函数）

求解 \(p\) 数组的过程是差不多的。

Code:

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e7+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
char a[N],b[N];
int n,m;
string s1,s2;
int z[N],p[N];
int l,r;
int ans1,ans2;
signed main()
{
	cin>>s1>>s2;
	n=s1.size(),m=s2.size();
	for(int i=1;i<=n;i++) a[i]=s1[i-1];
	for(int i=1;i<=m;i++) b[i]=s2[i-1];
	z[1]=m,l=0,r=0;
	for(int i=2;i<=m;i++){
		if(i<=r) z[i]=min(z[i-l+1],r-i+1);
		while(b[i+z[i]]==b[1+z[i]]) z[i]++;
		if(i+z[i]-1>r) r=i+z[i]-1,l=i; 
	}
	for(int i=1;i<=m;i++){
		ans1^=(z[i]+1)*i;
	}
	l=0,r=0;
	for(int i=1;i<=n;i++){
		if(i<=r) p[i]=min(z[i-l+1],r-i+1);
		while(a[i+p[i]]==b[1+p[i]]&&i+p[i]<=n&&1+p[i]<=m) p[i]++;   
			//注意这里要判断边界 
		if(i+p[i]-1>r) r=i+p[i]-1,l=i;
	}
	for(int i=1;i<=n;i++){
		ans2^=(p[i]+1)*i;
	}
	printf("%lld\n%lld\n",ans1,ans2);
	return 0;
}

本博客参考的网址：

[C++]洛谷：【模板】扩展 KMP（Z 函数） 算法详解