二维哈希

前置知识：字符串哈希

我们定义一个字符串 \(s\) 的哈希值为: \(\sum _ {i = 1} ^ n s[i] \times p_1 ^ {n-i}\)。

其中 \(n\) 是字符串的长度，下标从 \(1\) 开始，\(p_1\) 是一个稍微大一点的质数

如果我们要知道字符串 \(s\) 区间 \([l,r]\) 的哈希值,我们要先求出 \(s\) 的每一个前缀字符串的哈希值，令 \(h[i]\) 表示前 \(i\) 个字符组成的字符串的 \(hash\) 值，则：\(Hash([l,r])=h[r]-h[l-1] \times p_1 ^ {r-l+1}\)。
（可以把原字符串想象成一个 \(p\) 进制数来理解）。

定义

我们定义一个 \(n\) 行 \(m\) 列的矩阵 \(s\) 的哈希值为： \(\sum _{i=1}^n f[i] \times p2^{n-i}\)。
\(f[i]\) 是第 \(i\) 行的哈希值，\(p_2\) 是一个不同于 \(p_1\) 的质数。
并设 \(h[i][j]\) 表示矩形 \(s\)，前 \(i\) 行前 \(j\) 列组成的矩形的哈希值。

于是可以得出求解 \(h\) 数组的代码:

void Hash1()
{
	for(int i=1;i<=n;i++)
	{
		unsigned long long tmp=0;
		for(int j=1;j<=m;j++)
		{
			tmp=tmp*p1+s[i][j]-'a';
			h[i][j]=tmp+h[i-1][j]*p2;
		}
	}
}

我们希望对于二维哈希也可以像一维哈希那样能得到任意一个子矩阵的哈希值。
我们用一道例题来详细说明。

例题

acwing 矩阵

对于每一个询问，先处理出小矩阵的哈希值，接着枚举大矩阵的每个点，如果能 \(O(1)\) 求出以这个点为右下角端点的大小为 \(A\times B\) 的矩阵的哈希值，就可以 \(O(1)\) 判断了。

那怎么求呢？
以 \(n=6,m=8,i=5,j=6,a=2,b=3\) 为例（\((i,j) 使我们枚举到的点的下标\)），下面每个格子代表一个字符，红色部分即为所求：(格子里的是那个字符的坐标) 。

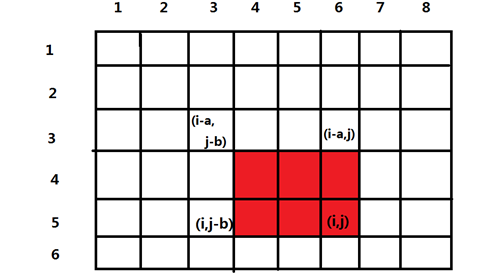
用 \(h[i][j]-h[i-a][j] \times p_2^a\) 就得到了蓝色部分。

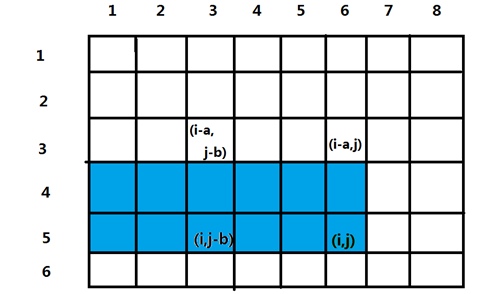
我们再减掉黄色部分其实就可以得到答案了。

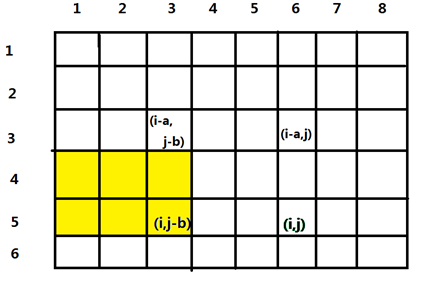
那黄色部分怎么求呢?

黄色部分其实就是 \(h[i][j-b]-h[i-a][j-b] \times p_2^a\)。

但是在蓝色部分-黄色部分的时候黄色部分整体要乘上 \(p_1^b\)。

所以答案就是
\(h[i][j] - h[i-a][j] \times (p_2)^a - ( h[i][j-b] - h[i-a][j-b] \times (p_2)^a) \times (p_1)^b\)

\(= h[i][j] - h[i-a][j] \times (p_2)^a - h[i][j-b] \times (p_1)^b + h[i-a][j-b] \times (p_2)^a \times (p_1)^b\)

其实和前缀和是一样的。

最后附上完整代码：

#include<bits/stdc++.h>
#define int long long
#define PII pair<int,int>
using namespace std;
const int N=1e5+5;
const unsigned long long p1=100003,p2=133331;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m,a,b,q;
unsigned long long m1[1005],m2[1005];
char s[1005][1005]; 
unsigned long long h[1005][1005];
unsigned long long g[1005][1005];
void Hash1()
{
	for(int i=1;i<=n;i++)
	{
		unsigned long long tmp=0;
		for(int j=1;j<=m;j++)
		{
			tmp=tmp*p1+s[i][j]-'0';
			h[i][j]=tmp+h[i-1][j]*p2;
		}
	}
}
map<unsigned long long,bool> mp;
char t[1005][1005];
unsigned long long Hash2()
{
	unsigned long long hsh=0;
	for(int i=1;i<=a;i++)
	{
		unsigned long long tmp=0;
		for(int j=1;j<=b;j++)
		{
			tmp=tmp*p1+t[i][j]-'0';
		}
		hsh=hsh*p2+tmp;
	}
	return hsh;
}
signed main()
{
	m1[0]=m2[0]=1;
	for(int i=1;i<=1000;i++) m1[i]=m1[i-1]*p1,m2[i]=m2[i-1]*p2;
	n=read(),m=read(),a=read(),b=read();
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			cin>>s[i][j];
		}
	}
	Hash1();
	for(int i=a;i<=n;i++)
	{
		for(int j=b;j<=m;j++)
		{
			g[i][j]=h[i][j]-h[i][j-b]*m1[b]-h[i-a][j]*m2[a]+h[i-a][j-b]*m1[b]*m2[a];
			mp[g[i][j]]=1; 
		}
	}
	q=read();
	while(q--)
	{
		for(int i=1;i<=a;i++)
		{
			for(int j=1;j<=b;j++)
			{
				cin>>t[i][j];
			}
		}
		unsigned long long hsh=Hash2();
		if(mp[hsh]) cout<<1<<endl;
		else cout<<0<<endl;
	}
	return 0;
}