CF做题总结

CF 做题总结

• ps：未放代码的是未调出来的，巨佬们可以帮帮蒟蒻。

CF1A

Describe

用 \(a \times a\) 的石块去覆盖 \(n \times m\) 的广场，问最少要用多少石块，可以超出广场，但是不可切割。

Solution

水题，可以用 \(ceil\)，但精度貌似要处理一下，所以直接判断也可以。

Code

1A - Theatre Square

---

CF1B

Describe

对于二维空间的 \((x, y)\) 有 \(2\) 中描述方法

• \(RxCy\)

\(x, y\) 表示坐标。

• \(Sx\)

\(x\) 表示坐标，\(S\) 表示 \(y\) 用如下方法加密

\(y = 1 : S = A\)

\(y = 26 : S = Z\)

\(y = 27 : S = AA\)

Solution

题目不难，但是细节很多，还未过。。

Code

---

CF1C

Describe

你有 \(3\) 个点，现在问你以这三个点为顶点的多边形的最小值。

Solution

比较有意思的题目，是个计算几何题。

首先，我们先不管正几边形是最小，假设我们已经知道了。

那么这个正多边形肯定在这三点所构成的外接圆上，这自行理解。

接下来我们的问题就是如何找到正几边形是最小的。

考虑在圆上，借用下题解里的图

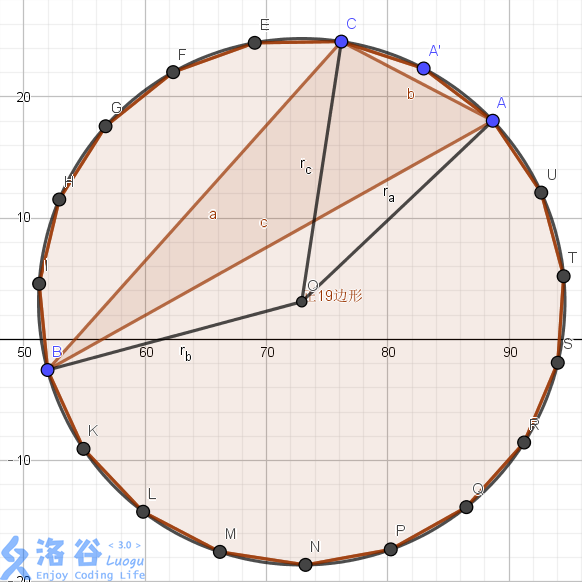
那么我们知道了 \(3\) 个点的坐标，可以找到以下东西。

外接圆半径，\(3\) 条边的长度。

考虑在三角形 \(ACO\) 中，我们知道了 \(3\) 条边，可以推出角 \(AOC\) 的大小。

同理可以求出角 \(BOC\) (这里我们假设 \(c\) 在 \(a, b\) 中间)

那么通过弧与圆心角相对应，我们可以知道。

正多边形在 \(a, c\) 之间的数目比上角 \(AOC\) 应该等于正多边形在 \(b, c\) 之间的数目比上角 \(BOC\) 。

那么我们可以发现正多边形相邻顶点对应圆心角应该是角 \(AOC\) 和角 \(BOC\) 的最小公约数。

那么再推出这个小三角形的面积乘以定顶点数就行了。

Code

1C - Ancient Berland Circus

---

CF2A

Describe

有 \(n\) 个回合，每个回合会有一个人增加一定分数(可以为负)，问最后的最高分 \(m\) 为多少，如有相同则输出最早不低于 \(m\) 的玩家。

Solution

\(Map\) 的板子题。

用 \(Map\) 计数，处理下细节就行了。

Code

2A - Winner

---

CF2B

Describe

有一个 \(n \times n\) 的矩阵，每个节点都有权值，你从左上角开始移动，每次可以向下或向右移动，把沿途的数相乘。问后缀的 \(0\) 的最小值。

Solution

考虑后缀 \(0\) 是如何得来的。

肯定是由 \(min\){因子 \(2\) 的个数， 因子 \(5\) 的个数}

一眼 \(DP\) ，记录 \(f_{i, j, 0 / 1}\) 当前到了 \((i, j)\) 这个点的最少 \(2/5\) 数量。

然后转移就很显然了，不过每次需要记录下来源，方便输出。

把 \(f_{i, j, 0}\) 和 \(f_{i, j, 1}\) 分开转移

这个时候你会问了，如果 \(2\) 个值从不同的路径转移过来，那岂不是不能取 \(min\) ？

其实是可以的，你考虑，如果这里可以取到 \(min\) ，那么这条路径取的 \(min\) 也可以取到这个 \(min\) 那么不就行了？

换句话说，就是你转移的是因子 \(2\) 和 \(5\) 的最小值，只有满足一个最小，就是全局最小。

Code

---

CF2C

Describe

在平面上有三个没有公共部分的圆，求平面上一点使得到三个圆的切线的夹角相等。

Solution

又是计算几何，这题血妈不止蓝题好吧。

容易得出：\(\frac{r_A}{dis(A,T)} = \frac{r_B}{dis(B,T)} = \frac{r_C}{dis(C,T)}\)

稍加转换：\(\frac{r_A}{r_B} = \frac{dis(A,T)}{dis(B,T)}\)

那么我们只要找到一个点 \(t\)，满足他到 \(2\) 个点的距离符合给定比例。

我们设出 \(k = \frac{\sqrt{(x_t - x_a) ^ 2 + (y_t - y_a) ^ 2}}{\sqrt{(x_t - x_b) ^ 2 + (y_t - y_b) ^ 2}}\)

平方一下，然后乘以分母。可以得到 \((k ^ 2 - 1) \times x_T ^ 2 + (k ^ 2 - 1) \times y_T ^ 2 - 2(k ^ 2 \times y_B - y_A) \times y_T - 2(k ^ 2 \times x_B - x_A) \times x_T + k ^ 2 \times x_B ^ 2 - x_A ^ 2 + k ^ 2 \times y_B ^ 2 - y_A ^ 2 = 0\)

我们把 \(k\) 看做常数，那么原方程可以化成一个 \(A \times x ^ 2 + A \times y ^ 2 + B \times x + C \times y + D = 0\)

有点常识的人就可以知道这是圆的一般方程，然后再分 \(2\) 种情况讨论。

• \(k = 1\)

那么 \(t\) 的轨迹是一条直线。

• \(k != 1\)

只需要把三个圆两两向交，再分开判断就行了。

Code

---

CF3A

Describe

在 \(8 \times 8\) 的棋盘上，输出用最少步数从起点走到终点的方案.

Solution

随便贪心一下就可以了

\(Cdoe\)

3A - Shortest path of the king

---

CF3B

Describe

你有 \(n\) 个物品，每个物体的体积为 \(1/2\)，并且有 \(p_i\) 的价值。

你最多可以选择体积和为 \(v\) 的物体，问最大价值。

Solution

这题一眼看上去像是一道裸的 \(0/1\) 背包问题。

但是你会发现这题的数据范围根本跑不了 \(0/1\) 背包。

然后你发现体积只有 \(1/2\) ，所以可以考虑贪心的配对，把体积为 \(1\) 的配对成很多体积为 \(2\) 的。

如果 \(n\) 为奇数就取一个最大的体积为 \(1\) 的，然后再配对。配对完之间贪心即可。

Code

3B - Lorry

---

CF3C

Describe

给你一个 \(3 \times 3\) 的井字格，玩井字棋游戏，给你一个状态，问当前是谁下\((first/second)\) 或者是非法 \((illegal)\) 胜利 \((the first/second player won)\) 平局 \((draw)\)

Solution

暴力。

Code

3C - Tic-tac-toe

---

CF3D

Describe

一个序列，序列中有左括号和右括号以及问号，问号可以替代为左括号和右括号，不过每次都有代价，并且变成的括号不同代价不一样，求最小代价。

Solution

---

CF4A

Describe

给你一个正整数 \(n\)， 问你可不可以把他分成 \(2\) 个正偶数。

Solution

水。

Code

4A - Watermelon

---

CF4B

Describe

你每个时刻有一个区间，你可以在区间中取值。要求最后相加为一个数 \(num\).

Solution

水。随便贪心下就行了。

Code

4B - Before an Exam

---

CF4C

Describe

每次回给你一个字符串，问你有没有出现过，若出现过则输出用户名 \(+ i\) , \(i\) 是数据库内的最小的 \(i\)。

Solution

水。可用 \(hash\) ……

Code

4C - Registration System

---

CF4D

Describe

每个点都有 \(2\) 个信息 \(w_i\) 和 \(h_i\) 。

你要求最长的二维严格上升子序列，并且输出长度以及每个物品。

Solution

和 \(LIS\) 的 \(dp\) 作法一样去做，不过多了一个约束而已。

记得记录以下路径。

Code

4D - Mysterious Present

---

CF5A

Describe

你有可能进行 \(3\) 种操作。

• 把一个人加入聊天

• 把一个人删除聊天

• 向所有正在聊天的发送信息。

问共发出多少信息。

Solution

随便乱搞

Code

5A - Chat Servers Outgoing Traffic

---

CF5B

Describe

给你一些字符，你要把他们用 \("*"\) 围起来，并且居中放置。

Solution

乱搞。。

Code

5B - Center Alignment

---

CF5C

Describe

给你一个括号序列，问最长的合法子串。合法的定义是左右括号匹配。

Solution

随便 \(dp\) 就行了。

分 \(2\) 中情况讨论。

Code

5C - Longest Regular Bracket Sequence

---

CF5D

Describe

你有一个加速度，和速度上限。你要满足在 \(d\) 位置时的速度不大于 \(w\) 问你最少需要多少时间到达 \(l\) 。

Solution

蠢王题，你只要稍微有点物理常识就可以做对。

不知道这题的意义是啥，又不卡精度，又不卡代码。

Code

5D Follow Traffic Rules

---

CF5E

Describe

你有 \(n\) 座山，在一个圆弧上，如果 \(2\) 座山之间没有比他们高的山，那么可以看到彼此。问最后有多少对可以看到彼此的山。

Solution

普通 \(dp\) 很裸，复杂度 \(O(n ^ 2)\)

设 \(l[i]\) 表示 \(i\) 左边的第一个比 \(i\) 高的位置，

设 \(r[i]\) 表示 \(i\) 右边的第一个比 \(i\) 高的位置。

求出这 \(2\) 个东西以后就可以 \(O(n)\) 的去求所需要求的了。

然后这 \(2\) 个东西可以用单调栈维护。

就没了。

Code

5E - Bindian Signalizing

---

CF6A

Describe

你有 \(4\) 木棍。

如果有 \(3\) 根可以组成三角形，输出 \(TRIANGLE\)

如果有 \(3\) 根可以满足任意 \(2\) 边只和大于另一条边，则输出 \(SEGMENT\)

不然则输出 \(IMPOSSIBLE\)

Solution

水。

注意判断的优先级。

Code

6A - Triangle

---

CF6B

Describe

一个 \(n \times m\) 的矩阵，每个位置上有相应的字符。

问你办公室有多少大。

Solution

随便模拟。

Code

6B - President's Office

---

CF6C

Describe

\(n\) 个糖，\(a\) 从前往后吃，\(b\) 从后往前吃，每个糖都有吃完需要的时间，每个人在同一时间只能吃一个，吃完某一个后，才能吃下一个，如果两个人同时开始吃同一个，\(b\) 会让给 \(a\) ，问最后每个人总共吃了多少糖

Solution

按题意模拟。

Code

6C - Alice, Bob and Chocolate

---

CF6D

Describe

有 \(n\) 个人，你可以用火球点某人，会对他造成 \(a\) 点伤害，对他旁边的人造成 \(b\) 点伤害。

问最少多少次打死所有人。

Solution

\(f_{i, j, k}\) 表示放到了 \(i\) ，第 \(i - 1\) 个人放了 \(j\) 个，第 \(i\) 个人放了 \(k\) 个。

转移 \(O(n * u ^ 3)\)

用后缀优化可以变成 \(O(n * u ^ 2)\)

Code

6D - Lizards and Basements 2

---

CF6E

Describe

给你一个长度为 \(n\) 的序列，问最长的子串满足元素差不超过 \(k\) ，以及个数，和每个子串的起始，终止位置。

Solution

\(O(n ^ 2)\) 的做法很显然，考虑怎么优化。

这题的单调性不是很显然吗？？？

那就用单调队列随便搞下不就行了？？？

Code

6E - Exposition

---

CF7A

Describe

你有一个 \(8 \times 8\) 的棋盘，你每次可以把一行或者一列变成黑色。问至少要多少次才可以变成目标棋盘。

Solution

判下就行了。

Code

7A - Kalevitch and Chess

---

CF7B

Describe

模拟题不多赘述。

Solution

模拟题不多赘述。

Code

7B - Memory Manager

---

CF7C

Describe

求 \(A \times x + B \times y + C = 0\) 的一组整数解 \((x, y)\)

Solution

\(exgcd\) 裸题。

不会 \(exgcd\) 的可以去看我的博客

Code

7C - Line

---

CF7D

Describe

一个长度为 \(n\) 的字符串 \(s\) 被叫做 \(k\) 阶级回文串，当且仅当它本身是一个回文串，而且它长度为 \(\frac{n}{2}\) (向下取整)的前缀和后缀都是 \(k - 1\) 阶级回文串.问所有前缀的阶级之和。

Solution

你发现对于一个前缀，只要满足， \(1 \to \frac{n}{2}\) 是一个阶级回文串，且 \(\frac{n}{2} \to n\) 也是一个阶级回文串。

那么显然这个东西满足拓扑序，也就是无后效性。

就可以 \(dp\) 了。

Code

7D - Palindrome Degree

---

CF7E

Describe

给你 \(n\) 个定义，以 \(#define\) 为开头。

形如 \(#define A B\) 即在接下来的运算中，会用 \(B\) 代替 \(A\)。

重定义完后，会给你一行，表示想要你计算的东西。

问你替代完以后会不会改变原式的运算顺序，如改变，则输出 \(Suspicious\) ，不然则输出 \(OK\)。

Solution

考虑我们只有 \(3\) 中情况是错误的：

• 前面是减法或者乘除法，而后面是没有括号的加减法运算。

• 前面是除法，后面是没有括号的乘除法。

• 前面是没有括号的加减法，后面是乘除法。

Code

7E - Defining Macros

---

CF8A

Describe

给你三个字符串 \(a, b, c\)，问你在字符串 \(a\) 的正序或倒序中是否有 \(b\)， \(c\) 这 \(2\) 个子串。

Solution

通过 \(string\) 的一些小函数可以轻松处理。

Code

8A - Train and Peter

---

CF8B

Describe

给你一个字符串，表示行走的路径，问你知否为最短。

Solution

判断下有无第 \(3\) 中元素出现即可。

Code

8B - Obsession with Robots

---

CF8C

Describe

给你一个起点和一些点的坐标，要你遍历每个点，并且从起点出发后一次最多只能到达 \(2\) 个不同的点。

Solution

考虑状压，首先我们设计状态 \(s\) 表示当前哪些物品已经被取回来了。

这样子我们可以每次 \(O(n ^ 2)\) 选择 \(1\) 个或者 \(2\) 个没取过的物品加入状态，然后 \(naive\) 的 \(dp\) 就行了。

这样做的复杂度是 \(O(n ^ 2 \times n ^ 2)\) 的，如果跑 \(24\) 的数据范围可能会 \(T\) 飞。

但是时限有 \(4s\) 而且是 \(CF\) 的题，说不定可以靠着信仰的 \(O_2\) 爆艹过去。

我们的复杂度的瓶颈是那个枚举没用过的点的 \(O(n ^ 2)\)

那我们来想如何优化到 \(O(n \times 2 ^ n)\)

因为我们这个有一个性质，对于这 \(2\) 中取法是没有区别的：

• 先取 \((1,2)\) 再取 \((3,4)\)

• 先取 \((3,4)\) 再取 \((1,2)\)

那么我们转移就不用这样转移了，我们就假设我们第一个点一定是当前没加入第一个点，因为先后不影响结果，所以可以直接这么搞。

然后 \(O(n)\) 的枚举其他点。

换句话说，这个转移没有时效性，之和最后的结果有关，与顺序无关，

所以我们 \(O(n^2)\) 的转移会出现很多无用的状态，减去即可。

对于一类互不干扰的状态，都可以用这种技巧，消掉一个 \(n\) 的复杂度。

Code

[C - Looking for Order](

---

CF482A

Descibe

求构造一个 \(n\) 的排列，要求相邻 \(2\) 个数相减所得到的绝对值刚好 \(k\) 种。

Solution

考虑对于一个排列 \(k\) ，他最多并且一定可以构造出 \(k - 1\) 个相邻的不同值。

这是个很 \(naive\) 的问题。

只要第一个放最小的，第二个放最大的，第三个次小的，第四个次大的…… 依次类推，每相邻的 \(2\) 个数的差都一定不一样。

然后在一个排列 \(n\) 中，要求 \(k\) 个不同的。

那你就从长度为 \(n\) 的排列中，随便取一段长度为 \(k\) 按照之前那个 \(naive\) 的作法搞一遍，其他按字典序排序就行了。

Code

482A - Diverse Permutation

---

CF570B

Describe

给你 \(2\) 个数，求一个数 \(a (1 <= a <= n)\), 使得当 \(c\) 在 \(1\) 到 \(n\) 的整数中 随机取值时, \(|c - a| < |c - m|\) 成立的概率最大。

Solution

考虑 \(c\) 的取值一直是在 \(m - 1\) 或者 \(m + 1\) 中取一个。

Code

570B - Simple Game

---