近三年以来联赛总结(2017~2019)

近三年以来联赛总结

\(ps\) 因为窝太菜了,不是所有题目都写了满分做法

2017 年

Day1

T1 小凯的疑惑

题目大意

给你 \(2\) 个数，每个数你都可以用无数次去构成新的数，问最大你不可以构成的数。

数据范围：

对于 \(30\%\) 的数据： \(1 \le a,b \le 50\)。

对于 \(60\%\) 的数据： \(1 \le a,b \le 10^4\)。

对于 \(100\%\) 的数据：\(1 \le a,b \le 10^9\)。

题解

这 就 是 小 学 奥 数 题 么

看到样例和数据范围大概就可以推出这是个结论题，然后打个表好像就行了= =

具体可以得到最后的答案是 \(a * b - (a + b)\)

知识点总结

这个题很好的考察的应考能力，有能力的可以通过 \(exgcd\) 优雅展开。

而未接触过的可以通过打表等方法找到规律。

标签

简单数学

代码

\(100ps\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#define maxn 50010
#define maxm 1000010
#define ls x << 1
#define rs x << 1 | 1
#define inf 10000000000
#define inc(i) (++ (i))
#define dec(i) (-- (i))
// #define mid ((l + r) >> 1)
#define int long long
#define XRZ 212370440130137957
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
}
signed main() { int a = read(), b = read();
	printf("%lld", (a - 1) * b - a);
	return 0;
}

T2 时间复杂度

题目大意

这是个模拟，题意从链接中自阅吧。

题解

按题意以及样例分析就行了。

先分析 \(ERR\) 的情况，这有2种情况。

第一种，在循环 \(F i x y\) 中 \(x\) 大于 \(y\)。

第二种，一段代码中未出现 \(E\)。

分析每个 \(F i x y\) 若 \(y = n\) && \(x != n\) 那么 ++ \(num\)

最后判断下 \(num\) 和复杂度的关系就行了。

好像也不是很麻烦

知识点分析

作为一道大模拟，还是不应该出现在 \(NOIP\) 上的吧，很容易弄坏别人的心态。

估计被喷的很惨

思路简单，但细节比较多，考验考生的代码能力，以及一些字符读入的方法。我好像 \(getchar\)，\(getline\)，\(cin\)，\(scanf\) 都用到了。

标签

模拟

代码

\(45ps\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#define maxn 50010
#define maxm 1000010
#define ls x << 1
#define rs x << 1 | 1
#define inf 10000000000
#define inc(i) (++ (i))
#define dec(i) (-- (i))
// #define mid ((l + r) >> 1)
//#define int long long
#define XRZ 212370440130137957
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
} int n; string s; bool vis[30];
signed main() { file(a); int T = read();	
	while(T --) { scanf("%d ", &n); getline(cin, s); int num = 0, Ans = 0, len = s.size(), std, flag = 0, QwQ = 0; mem(vis, 0);
		cout << s << endl;
		Rep(i, 0, len - 1) if(s[i] == '(') { int qwq = 0;
			Rep(j, i + 3, len - 2) qwq = qwq * 10 + s[j] - '0';// printf("qwq : %d\n", qwq);
			if(s[i + 1] == 'n') std = 100 + qwq;
			else std = s[i + 1] - '0';// printf("%c %d\n", s[i + 1], std);
		}// printf("std : %s %d\n", s, n);
		Rep(k, 1, n) { getline(cin, s); len = s.size();// cout << "QwQ" << s << endl;//printf("sssssssss%s\n", s);
			if(s[0] == 'E') { flag = 1; Ans = max(Ans, num), num = 0, mem(vis, 0) continue;}
			if(flag) continue;// printf("woaiyy3314 %d\n", num); printf("xLXLXLXLLX %c\n", s[0]);
			else {// printf("flag : %d %d\n", flag, vis[s[2] - 'a']);
//				cout << endl;
//				cout << "！@#@！#" << n << " " << flag << " " << QwQ << " " << num << " " << s[3] << endl;
				if(vis[s[2] - 'a']) QwQ = flag = 1;//, debug()
				else { vis[s[2] - 'a'] = 1;// printf("zz: %d %c %c\n", vis[s[2] - 'a'], s[4], s[len - 1]);
					if(s[4] == 'n' && s[len - 1] != 'n') flag = 1;
					else if(s[len - 1] == 'n' && s[4] != 'n') num ++;//, printf("woaiyy1314 %d\n", num);
					else if(s[4] == 'n' && s[len - 1] == 'n') continue;
					else { int sx[5] = {0}, sum = 0;
						Rep(i, 4, len - 1) { if(s[i] == ' ') { ++ sum; continue; }
							sx[sum] = sx[sum] * 10 + s[i] - '0';// printf("kkk%d %d\n", sx[0], sx[1]);
						} if(sx[0] > sx[1]) flag = 1;
					} 
				}// debug()
			}
		}// 
		//printf("%d %d %d %d %d\n", n, flag, QwQ, num, std);
		if(QwQ) puts("ERR");
		else if(flag == 0) puts("ERR");
		else {
			if(std > 100) { printf("%d %d\n", std, Ans);
				if(std == Ans + 100) puts("Yes");
				else puts("No");
			}
			else {
				if(num == 0) puts("Yes");
				else puts("No");
			}
		}
	}
	return 0;
}

T3 逛公园

题目大意

给定一张图，给定起点和终点。求有多少从起点到终点的路径权值在 \(n + k\) 内，其中 \(n\) 为起点到终点的最短路。

数据范围：

测试点编号	\(T\)	\(N\)	\(M\)	\(K\)	是否有0边
1	5	5	10	0	否
2	5	1000	2000	0	否
3	5	1000	2000	50	否
4	5	1000	2000	50	否
5	5	1000	2000	50	否
6	5	1000	2000	50	是
7	5	100000	200000	0	否
8	3	100000	200000	50	否
9	3	100000	200000	50	是
10	3	100000	200000	50	是

感谢 @HJGranger 提供的表（（（ \(MD\) 太烂了

题解

考虑 \(k = 0\) 的情况，跑一把最短路就行了，\(30ps\) 就到手了。好像也只会这 \(30ps\)

再考虑 \(70ps\) 的无 \(0\) 边的情况。

然而，这题竟然是个 \(DP\) ？

转移肯定是从当前节点转移向下一最小的节点。

众所周知，最短路求出来的 \(Dis[]\) 有很多妙用，对于 \(Dis[i]\) 有它的意义（懵逼脸），就是它表示的是节点 \(i\) 到 \(n\) 的最短路。

\(SPFA（Dij）\) 分不清这个2个，反正我写的那个是逐步递进的，就是说是一个一个入队，判断的，而且每个只会判断一次，那么是不是会满足 \(DP\) 的无后效性呢？

仔细想想，好像有点道理。假设 \(dis_i\) 表示 \(1 \to i\) 的最短路径，那么有一个比较显然的结论，在长度不超过 \(dis_n + s\) 的任意一条 \(1\to n\) 路上的任意一个点 \(x\) 处，都满足 \(1\to x\) 的长度不超过 \(dis_x + s\)。因为如果超过了，即使 \(x\to n\) 取最短路也不可能救得回来。

那么设 \(dp_{i,j}\) 表示长度为 \(dis_i + j\) 的 \(1 \to i\) 的路径数。

转移方程是：

\[dp_{i,j} = \sum_{k,j}^{}{dp_{k, dis_i + j - len - dis_k}} \]

大概是这样吧= = 不太会 \(MD\)

再考虑有 \(0\) 边的情况 =_=

有 \(0\) 边，就会存在 \(0\) 环，所以要类似于 \(SPFA\) 判负环一样去解决这个 \(0\) 环。

大概是这样的吧 代码先咕着………………

图论忘得差不多了，滚去补漏了= =

关于图论，联赛大致应该复习：

最短路，最小生成树，拓扑排序，差分约束，一些连通性问题。

代码补了，但只有 \(90ps\) 据说后 \(10ps\) 是赛后的某位神仙给洛谷的加的，所以放 \(NOIP\) 上可能有 \(100ps\)

知识点分析

题目出的很好，把图论的很多知识都杂糅起来了，在考场上是一道很好的考察基础的题目。

在设计了一个比较玄妙的 \(dp\) ，十分美味。

标签

动态规划，最短路，记忆化搜索。

代码

\(90ps\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
#define maxn 200010
#define maxm 100
#define ls x << 1
#define rs x << 1 | 1
#define inf 10000000000
#define inc(i) (++ (i))
#define dec(i) (-- (i))
// #define mid ((l + r) >> 1)
//#define int long long
#define XRZ 212370440130137957
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
}
int n, m, QwQ, x, y, z, mod, head[maxn], cnt, dis[maxn], vis[maxn][maxm], dp[maxn][maxm], flag, book[maxn], use[maxn][maxm], T;
struct node { int id, v; bool operator < ( const node& x ) const { return v > x.v; }};
struct Edge { int to, nxt, w;} e[maxn << 1]; priority_queue< node> q;
void add( int x, int y, int z ) { e[++ cnt] = (Edge) { y, head[x], z}, head[x] = cnt;}
void spfa() { Rep(i, 1, n) dis[i] = inf; mem(book, 0); dis[1] = 0, q.push((node) { 1, 0});
	while(!q.empty()) { int u = q.top().id; q.pop(); if( book[u] ) continue; book[u] = 1;
		Next(i, u) { int v = e[i].to;
			if(dis[v] > dis[u] + e[i].w ) dis[v] = dis[u] + e[i].w, q.push((node){ v, dis[v] });
		}
	}
}
int dfs( int x, int s, int node) { int ans = 0;
	if(vis[x][s - dis[x]]) { flag = 1; return 0;}
	if(use[x][s - dis[x]] == node) return dp[x][s - dis[x]];
	if(x == n && s - dis[x] <= QwQ) ans = 1; vis[x][s - dis[x]] = 1;
	Next(i, x) { int v = e[i].to;
		if(e[i].w + s - dis[v] <= QwQ) ans += dfs(v, s + e[i].w, node); ans %= mod ; 
		if(flag) break; } vis[x][s - dis[x]] = 0, use[x][s - dis[x]] = node;
	return dp[x][s - dis[x]] = ans % mod;
}
signed main() { T = read();
	while(T --) { mem(vis, 0) flag = 0, mem(head, 0) cnt = 0;
		n = read(), m = read(), QwQ = read(), mod = read(); mem(dp, 0)
		Rep( i, 1, m ) x = read(), y = read(), z = read(), add(x, y, z);
		spfa(); int ans = dfs( 1, 0, T + 1);
		if(!flag ) printf("%d\n", ans); else puts("-1");
	}
	return 0;
}

Day1 总结

大概拿分 \(100 + 100 + 30\) 吧，在 \(NOIP\) 上的话都可能会多挂些分吧（？），然后就凉了吧= =

目前拿分 \(100 + 45 + 90\) /kk

\(T3\) 还是很毒瘤的，\(T2\) 更加的邪教， \(T1\) 就有些无语。

Day2

T1 奶酪

题目大意

给你 \(n\) 个相同大小的在同一空间的球，相交或相切的球可以连通，问有没有一条路径可以连通 \(0 \to h\)。

对于 \(20\%\) 的数据, \(n = 1,1 \le h, r \le 10,000\) ,坐标的绝对值不超过 \(10,000\) 。

对于 \(40\%\) 的数据, \(1 \le n \le 8, 1 \le h, r \le 10,000\) ,坐标的绝对值不超过 \(10,000\) 。

对于 \(80\%\) 的数据, \(1 \le n \le 1,000, 1 \le h, r \le 10,000\) ,坐标的绝对值不超过 \(10,000\)。

对于 \(100\%\) 的数据, \(1 \le n \le 1,000,1 \le h , r \le 1,000,000,000,T \le 20\) , 坐标的绝对值不超过 \(1,000,000,000\) 。

题解

如果 \(2\) 个球之间相交，那么就把他们放到一个并查集里面，做一遍并查集和并。

最后只需要判断每一个并查集是否和 \(0\) 与 \(h\) 都连通就行了。

至于如何判断 \(2\) 个球是否相切/相交。

就只需要判断 \(2\) 个球的球心距和 \(2 * r\) 的大小关系就行了。

空间内的 \(2\) 点距离公式在题干中给了，就不多赘述了。

最后查询的时候枚举每个与 \(0\) 和 \(h\) 相交/相切的球是否同属一个并查集就行了，这个可以在读入的时候边读入边 \(O(1)\) 处理。

知识点分析

还算比较基础吧，也只考察了并查集这个基础算法，但是对于没学过圆与圆的位置关系或者无法类比圆与球的 \(xxs\) 来说就是噩梦了=_=

标签

并查集，简单数学。

代码

\(100ps\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#define maxn 100010
#define maxm 1000010
#define ls x << 1
#define rs x << 1 | 1
#define inf 10000000000
#define inc(i) (++ (i))
#define dec(i) (-- (i))
// #define mid ((l + r) >> 1)
#define int long long
#define XRZ 212370440130137957
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
}
int T, n, tot1, tot2, fa[maxn], f1[maxn], f2[maxn], x[maxn], y[maxn], l[maxn]; bool ans;
double dis(int x, int y, int z, int x1, int y1, int z1) { return sqrt((x - x1) * (x - x1) + (y - y1) * (y - y1) + (z - z1) * (z - z1));}
int find(int x) { return fa[x] == x ? fa[x] : fa[x] = find(fa[x]);}
signed main() { T = read();
	while(T --) { int n = read(), h = read(), r = read(); tot1 = tot2 = 0;
		Rep(i, 1, n) fa[i] = i;
		Rep(i, 1, n) { x[i] = read(), y[i] = read(), l[i] = read();
			if(l[i] + r >= h) f1[inc(tot1)] = i;
			if(l[i] - r <= 0) f2[inc(tot2)] = i;
			Rep(j, 1, i) if(dis(x[i], y[i], l[i], x[j], y[j], l[j]) <= (r << 1)) if(find(i) != find(j)) fa[find(i)] = find(j);
		} ans = 0;
		Rep(i, 1, tot1) {
			Rep(j, 1, tot2) if(find(f1[i]) == find(f2[j])) { ans = 1; break;}
			if(ans == 1) break;
		}
		if(ans == 1) printf("Yes\n");
		else printf("No\n");
	}
	return 0;
}

T2 宝藏

题目大意

有 \(n\) 个点，以及 \(m\) 条可以造的边，你可以任意现在一个点作为起点，使整张图连通，连接每条边的代价是 \(l \times k\)

其中 \(l\) 是这条道路的长度， \(k\) 是全图的起点到这条道路起点所经过的点数(包括当前道路的起点和全图的起点)。

问代价最小值是多少。

对于 \(20\%\) 的数据： 保证输入是一棵树，\(1 \le n \le 8，v \le 5000\) 且所有的 \(v\) 都相等。

对于 \(40\%\) 的数据： \(1 \le n \le 8，0 \le m \le 1000，v \le 5000\) 且所有的 \(v\) 都相等。

对于 \(70\%\) 的数据： \(1 \le n \le 8，0 \le m \le 1000，v \le 5000\)

对于 \(100\%\) 的数据：\(1 \le n \le 12，0 \le m \le 1000，v \le 500000\)

题解

这数据范围，我貌似只会 \(2\) 种方法(指数据范围)

状压 \(dp\) 和 \(Dfs\) =_=

可能是我太菜了吧，不会满分的 \(Dfs\) ，那就只能想想 状压 \(dp\) 的做法趴。

什么是状压 \(dp\)

把一些状态转化成一个特定的进制数，每一位表示一个物体取或者不取，并且作为 \(dp\) 的一个维度不断转移。

那么不妨设 \(f_{i,j}\) 表示当前的状态为 \(j\)，当前节点和起点直接的节点数。

那么先把转移放出来：

\[f_{i,j} = min(f_{i - 1, k} + Num_{k, j} \times (i - 1)) \]

其中 \(k \in j\) \(Num_{k, j}\) 表示从状态 \(k\) 转移到 \(j\) 的最小路径。

\(Num[][]\) 则是可以预处理出来。

再来解释一下为什么可以这么转移。

\(f_{i,j}\) 只可能从 \(f_{i - 1, k}\) 转移而来，所以取了 \(min\) 以后，如果能保证柿子的正确那么就保证了结果的正确。

后面都讲了 \(Num_{k, j}\) 表示从状态 \(k\) 转移到 \(j\) 的最小花费，那自然就是对的了啊 = =

还有一个枚举子集的常见方法。

搞完以后去看了一波题解，发现第一篇就是神仙学长 \(sermoon\) 的 \(Dfs\) 满分做法，我…………

考试的时候估计会先写个 \(Dfs\) 的数据分治吧，不知道我的 \(Dfs\) 有么有 \(100ps\) /kk

知识点总结

很好的状压 \(dp\) 题，但是 \(Dfs\) 做法不知道是不是故意放过去的？

标签

\(Dfs\) , 状压 \(dp\)

代码

\(100ps\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#define maxn 15
#define maxm 5000
#define ls x << 1
#define rs x << 1 | 1
#define inf 10000000000
#define inc(i) (++ (i))
#define dec(i) (-- (i))
// #define mid ((l + r) >> 1)
#define int long long
//#define XRZ 212370440130137957
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
} int n, m, x, y, z, f[maxn][maxm], a[maxn][maxn], num[maxn][maxm];
signed main() { n = read(), m = read(); mem(a, 0x7f) mem(f, 0x7f) Rep(i, 1, n) f[1][1 << i - 1] = 0; int Ans = inf, N = (1 << n) - 1; // N是最大状态，也就是dp的第二维的上限 
	Rep(i, 1, n) a[i][i] = 0; Rep(i, 1, m) x = read(), y = read(), z = read(), a[x][y] = a[y][x] = min(a[x][y], z);
	Rep(i, 1, n) Rep(S, 0, N) { int tmp = inf; Rep(j, 1, n) if(S & (1 << j - 1)) tmp = min(tmp, a[i][j]); num[i][S] = tmp;}
	Rep(i, 2, n) Rep(S, 0, N) for(int s = S; s != 0; s = (s - 1) & S) { int tmp = 0, now = s ^ S; //这就是那个枚举子集的小妙招。 
		Rep(j, 1, n) if(now & (1 << j - 1)) tmp += num[j][s]; f[i][S] = min(f[i][S], f[i - 1][s] + (i - 1) * tmp);
	} Rep(i, 1, n) Ans = min(Ans, f[i][N]); printf("%lld\n", Ans);
	return 0;
}

T3 列队

题目大意

有一个 \(n \times m\) 的矩阵，最开始给每个点按照网络流的常见方法，即：

对于初始矩阵的一个位置 \((i,j)\) 给他编号\((i - 1) \times m + j\)

每次有人离队后，队列会有 \(2\) 个命令：

\(1\) .向左看齐。这时第一列保持不动，所有学生向左填补空缺。不难发现在这条指令之后，空位在第 \(x\) 行第 \(m\) 列。

\(2\) .向前看齐。这时第一行保持不动，所有学生向前填补空缺。不难发现在这条指令之后，空位在第 \(n\) 行第 \(m\) 列。

但是每次只能有一名学生离队，只有这个学生归队到 \((n,m)\) 的位置后，下一个学生才可以离队，并重新执行这 \(2\) 个命令。

编号不会随队列的改变而改变。求每次离队的学生的编号。

数据范围：

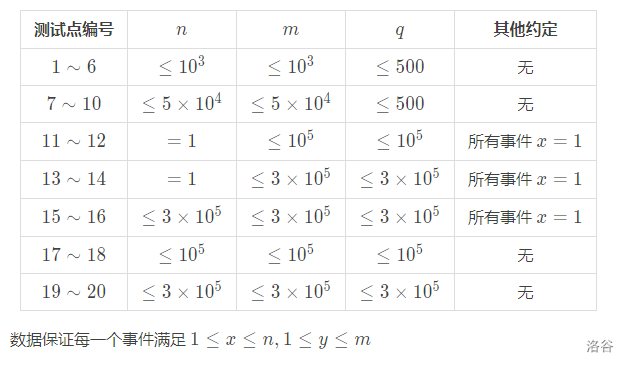
题解

先看部分分。

\(1 \to 10\) 直接取出所有询问用到的行和列，暴力模拟一些就行了。

\(11 \to 14\) 直接在系列上维护就可以了，比较裸。

对于 \(11 \to 16\) 的 \(x = 1\) 的点不会处理。就有 \(70ps\) 了。。。

然后开始讲 \(100ps\) 做法。

因为命令是有顺序的，所以除了最后一列有可能往前移之外，其他都只可能往左移。

那么需要维护的就只有每一行和最后一列，那么就建 \(n + 1\) 颗线段树维护信息就行了。

但是貌似会炸，所以要动态开点去建树。

至于维护什么信息，就是对于每颗线段树，考虑维护一段区间内，合法的数字个数。

如果删除一个数就把他的 \(size = 0\) ;并且把这个数加到 \(vector\) 里面。

最后查找 \((i, j)\) 的话就找第 \(i\) 线段树的第 \(j\) 个合法的位置，如果整颗线段树的 \(size\) 总和都小于 \(j\) 就从 \(vector\) 里面去继续找数。

记住要动态开点！！

知识点总结

首先，有个很妙的结论就是只和每一行和最后一列有关。

然后线段树的动态开点也是一个比较常见的技巧。

最后利用耗费空间很小的 \(vector\) 来记录那 \(q\) 个删除的数，而且 \(vector\) 也很方便查询。

标签

线段树，动态开点。

代码

\(100ps\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#define maxn 300010
#define maxm 6000010
#define ls e[p].l
#define rs e[p].r
#define inf 10000000000
#define inc(i) (++ (i))
#define dec(i) (-- (i))
#define mid ((l + r) >> 1)
#define int long long
#define XRZ 212370440130137957
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
} struct tree { int sum, l, r;} e[maxm << 2]; int tot, tree[maxn]; vector <int> g[maxn];
void update(int &p, int l, int r, int x, int y, int k) { if(p == 0) p = ++ tot; if(l == r) { e[p].sum += k; return;}
    if(mid >= x) update(ls, l, mid, x, y, k); if(mid < y) update(rs, mid + 1, r, x, y, k); e[p].sum = e[ls].sum + e[rs].sum;
} int query(int p, int l, int r, int k) { int len = mid - l + 1 - e[ls].sum; if(l == r) return l;
    if(len >= k) return query(ls, l, mid, k); else return query(rs, mid + 1, r, k - len);
} signed main() { int n = read(), m = read(), q = read(), Q = q;
	while(q --) { int x = read(), y = read(); 
        if(y == m) { int pos = query(tree[n + 1], 1, n + Q, x); update(tree[n + 1], 1, n + Q, pos, pos, 1);
            if(pos > n) printf("%lld\n", g[n + 1][pos - n - 1]), g[n + 1].push_back(g[n + 1][pos - n - 1]);
            else printf("%lld\n", pos * m), g[n + 1].push_back(pos * m);
        } else { int pos = query(tree[x], 1, m + Q - 1, y); update(tree[x], 1, m + Q - 1, pos, pos, 1);
            int p = query(tree[n + 1], 1, n + Q, x), tmp; update(tree[n + 1], 1, n + Q, p, p, 1);
            if(p > n) tmp = g[n + 1][p - n - 1]; else tmp = p * m;
            if(pos > m - 1) printf("%lld\n", g[x][pos - m]), g[n + 1].push_back(g[x][pos - m]), g[x].push_back(tmp);
            else printf("%lld\n", (x - 1) * m + pos), g[n + 1].push_back((x - 1) * m + pos), g[x].push_back(tmp);
        }
    }
	return 0;
}

Day2 总结

预计拿分 \(100 + 100 + 70\) 吧，考场上 \(T2\) 估计会写个记忆化搜索就跑路吧，不知道有没有 \(100ps\)

目前拿分 \(100 + 100 + 100\)

NOIP2017 总结

预计拿分 \(100 + 100 + 30 + 100 + 100 + 70\) ，

目前拿分 \(100 + 45 + 90 + 100 + 100 + 100\) ；

\(HN\) 省一分数线 \(290\)。

2018 年

Day1

T1 铺设道路

题目大意

给你一个序列 \(a_i\), 每次可以操纵一个不含 \(0\) 的区间，使区间里的所有数减 \(1\)

问最少几次操作可以使整个序列变为 \(0\) 。

数据范围：

对于 \(30\%\) 的数据，\(1 ≤ n ≤ 10\) ;

对于 \(70\%\) 的数据，\(1 ≤ n ≤ 1000\) ;

对于 \(100\%\) 的数据，\(1 ≤ n ≤ 100000 , 0 ≤ d_i ≤ 10000\) ;
​

题解

记 \(Ans\) 表示消除 \(1 \to i\) 需要的最小次数，如果 \(A_i < A_{i - 1}\) ，那么可以直接在消 \(A_{i - 1}\) 的时候消完 \(A_i\)，如果 \(A_i < A_{i - 1}\) ，那么在消完 \(A_{i - 1}\) 后还剩 \(A_i - A_{i - 1}\) ，这就是要补上的，统计一下即可。

知识点总结

比较简单的签到题，思维难度和代码难度都不大

标签

贪心。

代码

\(100ps\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#define maxn 1000010
#define maxm 1000010
#define ls x << 1
#define rs x << 1 | 1
#define inf 10000000000
#define inc(i) (++ (i))
#define dec(i) (-- (i))
#define mid ((l + r) >> 1)
#define int long long
#define XRZ 212370440130137957
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
}
int ans, A[maxn], n;
signed main() { int n = read();
	Rep(i, 0, n - 1) A[i] = read();
	Rep(i, 1, n - 1) if(A[i] > A[i - 1]) ans += A[i] - A[i - 1];
	printf("%d", ans + A[0]);
	return 0;
}

T2 铺设道路

题目大意

有 \(n\) 种不同面额的货币，第 \(i\) 种货币的面额为 \(a_i\) ，你可以假设每一种货币都有无穷多张。为了方便，我们把货币种数为 \(n\) 、面额数组为 \(a_{1 \to n}\) 的货币系统记作 \((n, a)\) 。

在一个完善的货币系统中，每一个非负整数的金额 \(x\) 都应该可以被表示出，即对每一个非负整数 \(x\)，都存在 \(n\) 个非负整数 \(t_i\) 满足 \(a_i \times t_i\) 的和为 \(x\) 。然而，在网友的国度中，货币系统可能是不完善的，即可能存在金额 \(x\) 不能被该货币系统表示出。例如在货币系统 \(n = 3, a = [2, 5, 9]\) 中，金额 \(1, 3\) 就无法被表示出来。

两个货币系统 \((n, a)\) 和 \((m, b)\) 是等价的，当且仅当对于任意非负整数 \(x\) ，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。

现在网友们打算简化一下货币系统。他们希望找到一个货币系统 \((m, b)\) ，满足 \((m, b)\) 与原来的货币系统 \((n, a)\) 等价，且 \(m\) 尽可能的小。他们希望你来协助完成这个艰巨的任务：找到最小的 \(m\)。

一句话题意：给定一个集合 \(A\) 让你找出一个集合 \(B\) 使得 \(A\) 中的所有元素都能被 \(B\) 中的一个和多个元素表示出来, 要求 \(B\) 的元素尽量少, 求 \(B\) 中最少的元素个数。

数据范围

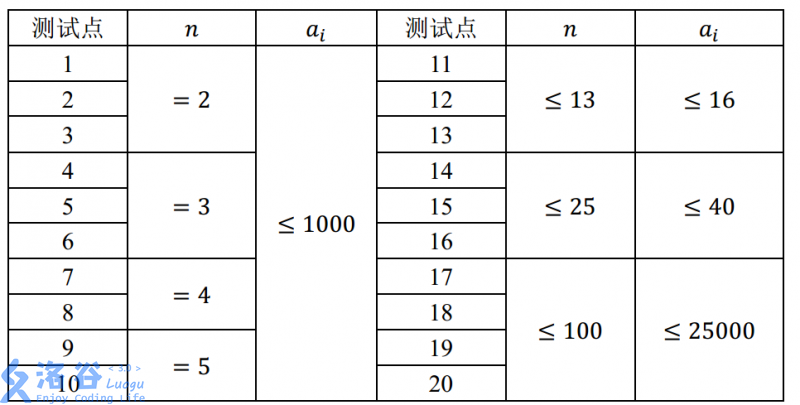
题解

算是个结论题吧，不多证明了~

先排个序, 一个数字一定只能由比它本身小的数字通过累加得到, 枚举 \(A\) 中的所有元素, 然后用判定性完全背包来确定哪一个数字能被表示, 每有一个数字能被表示, 就把原先等于 \(n\) 的 \(Ans --\) 最后输出 \(Ans\) 就完了。。。

知识点分析

比较秒的背包吧，前面套了一点数学知识 \((?)\) ，就是你要得出 \(B \subseteq A\) 这个东西，然后再 \(DP\)。

标签

\(DP\)， 数学，贪心 \((?)\)

代码

\(100ps\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <string>
#include <cmath>
#define N 25010
#define M (1 << 20) + 10
#define ls i << 1
#define rs i << 1 | 1
#define inf 0x3f3f3f3f
#define inc(i) (++ (i))
#define dec(i) (-- (i))
#define mid ((l + r) >> 1)
#define int long long
#define XRZ 1000000007
#define debug() puts("XRZ TXDY");
#define n_ ((n >> 1) + 1)
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
// #define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
// const int dx[10] = {1, -1, 0, 0};
// const int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
}
int f[N], a[N], n, t, ans;
signed main() { t = read();
	while(t --) { mem(f, 0); ans = n = read();
		Rep(i, 1, n) a[i] = read(); sort(a + 1, a + n + 1); f[0] = 1;
		Rep(i, 1, n) { if(f[a[i]]) { dec(ans); continue;}
			Rep(j, a[i], a[n]) f[j] = f[j] | f[j - a[i]];
		} printf("%d\n", ans);
	}
	return 0;
}

T3 赛道修建

题目大意

就是给你一颗 \(n\) 个点的树，你需要找到 \(m\) 条互不相交的赛道，赛道可以由若干条道路组成。

使得修建的 \(m\) 条赛道中长度最小的赛道长度最大（即 \(m\) 条赛道中最短赛道的长度尽可能大）

数据范围：

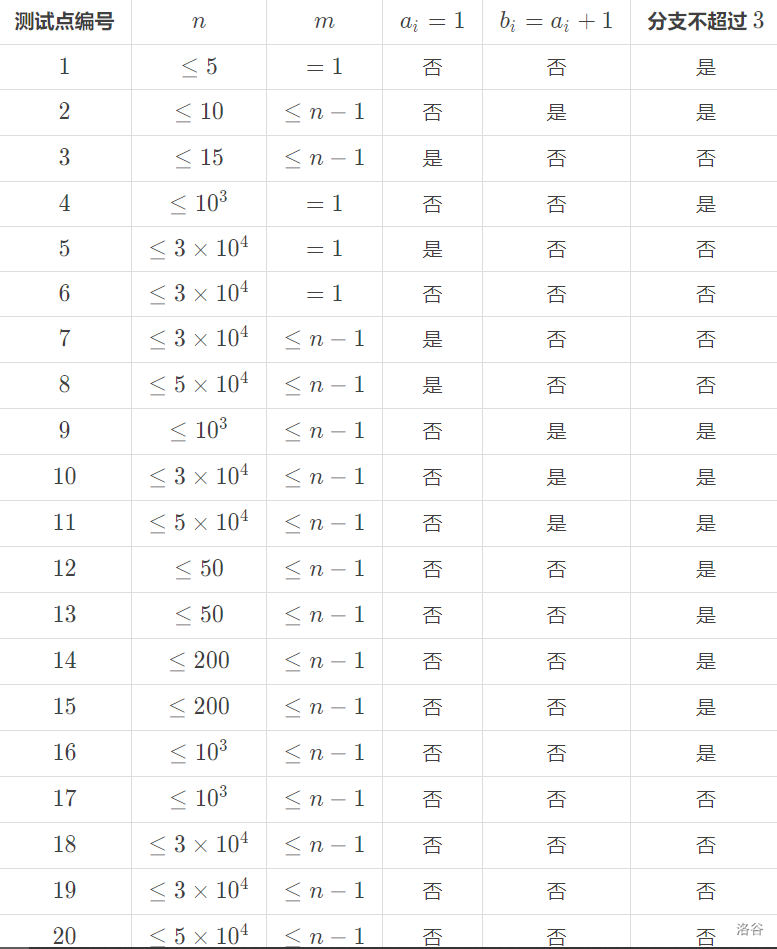
题解

部分分懒得讲了 \(QwQ\)

有点常识就可以看出这是颗树（废话，你的简要题意都讲了= =）

然后考虑二分长度，每次判断可不可行。

考虑每一条非连接叶节点和其他节点的边，只可能从其的一条子树向上传递（因为他只可以从父节点出去，而父节点只可以被遍历一遍）

那么你只需要看看当前这个节点的子链可以组成多少大于 \(mid\) 的赛道， \(Dfs\) 实现就行了。

没什么好说的= =

具体还是讲下实现，就是在 \(Dfs\) 回溯的过程中你不断的向上传递每一条子链的总长度，并且用一个 \(set\) 维护它。

如果在 \(set\) 中可以找到 \(2\) 条边加起来大于二分的 \(mid\)，先别直接删除。

要继续在 \(set\) 中二分查找的去找最小的一个子链可以满足 \(2\) 个子链相加大于 \(mid\) 再删除。

其余的未删除的子链就把最大的那一条向上传递，其余就已经作废，这个也是无后效性的。

代码感觉挺好写的，就是一直调不出， \(zbl =_=\)

知识点总结

考查的比较基础？没有什么很难的算法。。。思维难度偏大吧

标签

\(set\) ，\(Dfs\)

代码

\(100ps\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <set>
#include <cmath>
#define maxn 50010
#define maxm 1000010
#define ls x << 1
#define rs x << 1 | 1
#define inf 0x7fffffff
#define inc(i) (++ (i))
#define dec(i) (-- (i))
//#define mid ((l + r) >> 1)
#define int long long
#define XRZ 212370440130137957
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
} int u, v, w, s, tot, l, r = inf, Mid, now, ans, head[maxn], f[maxn];
struct edge { int v, nxt, w;}e[maxn << 1];
void add(int u, int v, int w) { e[++ tot].v = v, e[tot].w = w, e[tot].nxt = head[u], head[u] = tot;}
void dfs(int u, int fa) { multiset <int> s;
    Next(i, u) { int v = e[i].v; if(v == fa) continue; dfs(v, u);
        if(f[v] + e[i].w >= Mid) inc(now); else s.insert(f[v] + e[i].w);
    } while(!s.empty()) { multiset <int> :: iterator it = s.begin();
        int temp = *it; s.erase(it); it = s.lower_bound(Mid - temp);
        if(it == s.end()) f[u] = max(f[u], temp); else inc(now), s.erase(it);
    }
}
signed main() { int n = read(), s = read();
    Rep(i, 1, n - 1) u = read(), v = read(), w = read(), add(u, v, w), add(v, u, w);
    while(l <= r) { Mid = l + r >> 1; now = 0, mem(f, 0); dfs(1, 0);
        if(now >= s) ans = Mid, l = Mid + 1; else r = Mid - 1;
    } printf("%d", ans);
	return 0;
}

Day1 总结

预计拿分 \(100 + 100 + 55\) 还是要稳一点啊。

目前拿分 \(100 + 100 + 100\) 。

Day2

T1 旅行

题目大意

给你一颗 \(n\) 个节点，\(m\) 条边的图，你可以任选一个点作为起点遍历所有的节点，要求最后字典序最小。

数据范围：

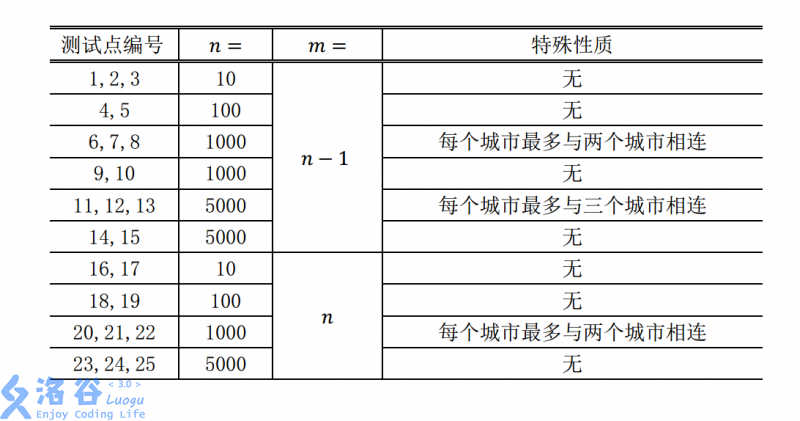
题解

只会 \(60ps\)。。

考虑只有 \(2\) 种情况。

第一种 \(n = m - 1\)

这种就只要跑一遍 \(Dfs\) 每次贪心的去找当前最小的没遍历过的下一节点。不用回溯。。。

第二种 \(n = m\)

这种情况就是一棵树加上一条边，也就是一颗基环树。

因为只要遍历一遍所有节点，那么有一条边是不用走的。

那么，就枚举所有的边，看看把他删除以后的最小字典序。

求法和第一种一样。

知识点总结

标签

贪心，\(Dfs\)

代码

\(60ps\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#define maxn 5010
#define maxm 1000010
#define ls x << 1
#define rs x << 1 | 1
#define inf 10000000000
#define inc(i) (++ (i))
#define dec(i) (-- (i))
#define mid ((l + r) >> 1)
#define int long long
#define XRZ 212370440130137957
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
} int u, v, w, cnt, n, QwQ, head[maxn], Pla[maxn], con[maxn][maxn], vis[maxn];
//struct node { int nxt, to;};
//void Add(int u, int v) { e[inc(cnt)] = (node) {head[u], v}; head[u] = cnt;}
void Dfs(int x, int n) { Pla[inc(QwQ)] = x, vis[x] = 1;
	Rep(i, 1, n) if(vis[i] == 0 && con[x][i]) Dfs(i, n);
}
signed main() { int n = read(), m = read();
	if(n == m + 1) {
		Rep(i, 1, m) u = read(), v = read(), con[u][v] = con[v][u] = 1;
		Dfs(1, n); Rep(i, 1, n) printf("%d ", Pla[i]);
	}
	else {
		puts("stO zz Orz");
	}
	return 0;
}

\(100ps\)

#pragma GCC optimize(fast)
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <string>
#include <vector>
#define maxn 5010
#define M 50
#define ls i << 1
#define rs i << 1 | 1
#define inf 0x7fffffff
#define inc(i) (++ (i))
#define dec(i) (-- (i))
#define mid ((l + r) >> 1)
#define int long long
#define XRZ 1000000007
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
}
int n, m, u, v, tot, cnt, QwQ, fa[maxn], h[maxn], a[maxn], Ans[maxn], U[maxn], V[maxn], Pla[maxn], con[maxn][maxn], vis[maxn];
bool book[maxn]; vector<int> G[maxn];
void dfs(int x, int n) { Pla[inc(QwQ)] = x, vis[x] = 1;
	Rep(i, 1, n) if(vis[i] == 0 && con[x][i]) dfs(i, n);
}
void Dfs(int u, int fa) { if(cnt > n) return; a[inc(cnt)] = u;
	Rep(i, 0, G[u].size() - 1) if(G[u][i] != fa && G[u][i]) Dfs(G[u][i], u);
}
signed main() { n = read(), m = read();
	if(n == m + 1) {
		Rep(i, 1, m) u = read(), v = read(), con[u][v] = con[v][u] = 1;
		dfs(1, n); Rep(i, 1, n) printf("%d ", Pla[i]);
	} else {
		Rep(i, 1, m) U[i] = read(), V[i] = read(), G[U[i]].push_back(V[i]), G[V[i]].push_back(U[i]);
		Rep(i, 1, n) sort(G[i].begin(), G[i].end()); mem(Ans, 0x3f); Rep(i, 1, m) { u = U[i], v = V[i];
		Rep(j, 0, G[u].size() - 1) if(G[u][j] == v){ G[u][j] = 0; break;}
        Rep(j, 0, G[v].size() - 1) if(G[v][j] == u){ G[v][j] = 0; break;}
		cnt = 0, mem(a, 0) Dfs(1, 0); if(cnt == n) { bool flag = 0;
			Rep(j, 1, n) { if(a[j] < Ans[j]){ flag = true; break;} if(a[j] > Ans[j]) break;}
			if(flag){ Rep(j, 1, n) Ans[j] = a[j];}
		}
		Rep(j, 0, G[u].size() - 1) if(G[u][j] == 0) { G[u][j] = v; break;}
        Rep(j, 0, G[v].size() - 1) if(G[v][j] == 0) { G[v][j] = u; break;}}
		Rep(i, 1, n) printf("%d ", Ans[i]);
	}
	return 0;
}

T2 填数游戏

题目大意

一个 \(n \times m\) 的矩阵，规定一条合法的路径只可以向右 \((R)\) 或下 \((D)\)

你可以给每个位置填上 \(0\) 或者 \(1\) 。求有多少种方案满足所有路径的 \(DR\) 和 \(01\) 同大或同小。

题解

太难写了，就先咕着，根本讲不清。

具体可以看这篇

知识点总结

没什么区分度= =

前 \(65\) 可以通过小表打出，后面考场上根本不可做。

标签

数学。

代码

推到 \(3\) 就有 \(65ps\)

但是我推到了 \(5\) 还是只有 \(65ps\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#define maxn 50010
#define maxm 1000010
#define ls x << 1
#define rs x << 1 | 1
#define inf 10000000000
#define inc(i) (++ (i))
#define dec(i) (-- (i))
#define mid ((l + r) >> 1)
#define int long long
#define XRZ 1000000007
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
}
int ksm(int a, int b) { int base = a, Ans = 1;
	while(b) { if(b & 1) Ans = Ans * base % XRZ;
		b >>= 1, base = base * base % XRZ;
	} return Ans;
} 
signed main() { int n = read(), m = read(); if(n > m) swap(n, m);
	if(n == 1) printf("%lld", ksm(2, m));
	else if(n == 2) printf("%lld", 4 * ksm(3, m - 1) % XRZ);
	else if(n == 3) printf("%lld", 112 * ksm(3, m - 3) % XRZ);
	else if(n == 4) { if(m == 4) puts("912"); printf("%lld", 2688 * ksm(3, m - 5) % XRZ);}
	else if(n == 5) { if(m == 5) puts("7136"); printf("%lld", 21312 * ksm(3, m - 6) % XRZ);}
	else puts("XRZ txdy");
	return 0;
}

T3 保卫王国

题目大意

一张图，每个点的权值可以为 \(0 / 1\) ，如果为 \(1\) 的话需要 \(p_i\) 代价， 但是要求相邻的节点必须至少有一个为 \(1\) 。

而且有 \(q\) 个要求，每次要求会给定 \(a, x, b, y\) 。

若 \(x\) 为 \(0\)，表示城市 \(a\) 不得驻扎军队。

若 \(x\) 为 \(1\)，表示城市 \(a\) 必须驻扎军队。

若 \(y\) 为 \(0\)，表示城市 \(b\) 不得驻扎军队。

若 \(y\) 为 \(1\)，表示城市 \(b\) 必须驻扎军队。

对于每次要求，你需要输出满足要求的总代价最小。

数据范围：

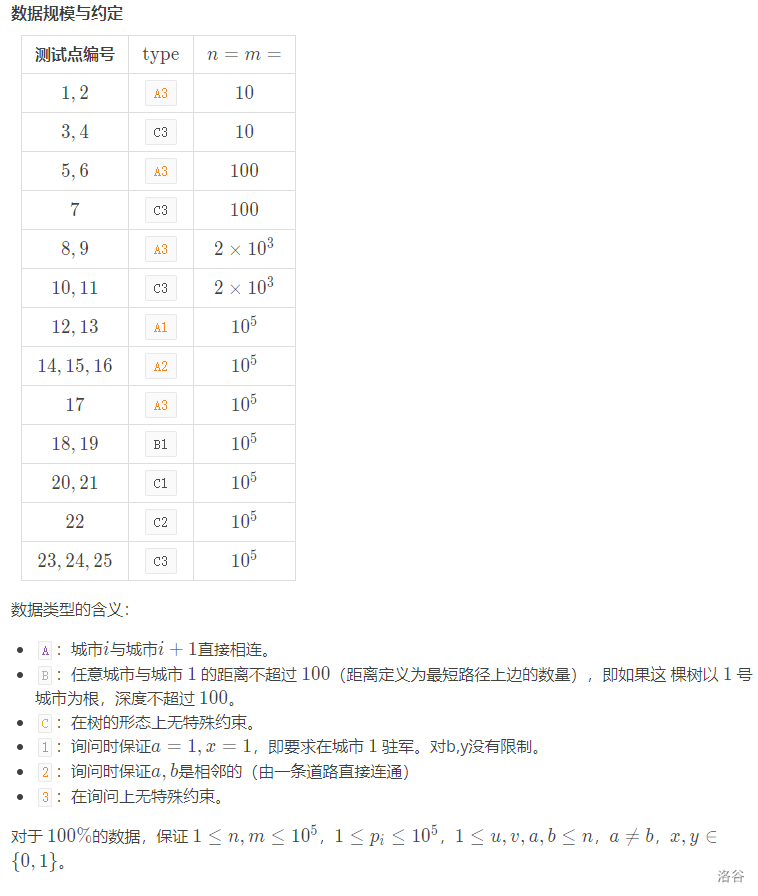
题解

这题的分比 \(T2\) 的后 \(35ps\) 好拿多了。

因为水平问题，这里只讲我会的部分分做法， 据说正解是动态 \(dp\)

首先，先看 \(n <= 2000\) && \(m <= 2000\) 的暴力 \(dp\)

可以考虑 \(f[i][0/1]\) 表示当前递归到了 \(i\) 节点，当前的节点是选还是不选的最小代价。

至于那 \(2\) 个点，每次打上标记就行了 \(f[a][x ^ 1] = f[b][y ^ 1] = inf\)

转移的话就是最朴素的树形 \(dp\) 的转移：

\[f[x][1] += min(f[v][0], f[v][1]) \]

\[f[x][0] += f[v][1] \]

\(f[x][1]\) 在递归的时候还需要加上选择这个节点的代价。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#define maxn 50010
#define maxm 1000010
#define ls x << 1
#define rs x << 1 | 1
#define inf 10000000000
#define inc(i) (++ (i))
#define dec(i) (-- (i))
#define mid ((l + r) >> 1)
#define int long long
#define XRZ 212370440130137957
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
} string s; struct node { int nxt, to; } e[maxn << 1]; int head[maxn], x, y, cnt, f[maxn][2], q[maxn];
void Add(int x, int y) { e[inc(cnt)] = (node) {head[x], y}; head[x] = cnt;}
void Dfs(int x, int fa) {
	Next(i, x) { int v = e[i].to;
		if(v == fa) continue; Dfs(v, x);
		f[x][1] += min(f[v][0], f[v][1]);
		f[x][0] += f[v][1];
	} f[x][1] += q[x];
}
void baoli_dp(int q) {
	while(q --) { int a = read(), x = read(), b = read(), y = read(); mem(f, 0)
		f[a][x ^ 1] = f[b][y ^ 1] = inf; Dfs(1, 0);
		if(f[1][1] >= inf && f[1][0] >= inf) puts("-1"); else printf("%d\n", min(f[1][1], f[1][0]));
	}
}
signed main() { int n = read(), m = read(); cin >> s;
	Rep(i, 1, n) q[i] = read();
	Rep(i, 1, n - 1) x = read(), y = read(), Add(x, y), Add(y, x);
	if(n <= 2000 && m <= 2000) baoli_dp(m);
	return 0;
}

再考虑 \(*1\) 的情况，这种情况一定会在 \(1\) 处驻军，那么就先把 \(1\) 处附上极大值 \(f[1][0] = inf\)

从叶节点向根 \(Dfs\) 一遍，再从根向叶节点 \(Dfs\) 一遍最后在 \(y\) 处相加就行了。

不知道为什么 \(T\) 了，但复杂度应该没问题

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#define maxn 100010
#define maxm 1000010
#define ls x << 1
#define rs x << 1 | 1
#define inf 10000000000
#define inc(i) (++ (i))
#define dec(i) (-- (i))
#define mid ((l + r) >> 1)
#define int long long
#define XRZ 212370440130137957
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
} string s; struct node { int nxt, to; } e[maxn << 1]; int head[maxn], x, y, cnt, f[maxn][2], q[maxn], ff[maxn][2];
void Add(int x, int y) { e[inc(cnt)] = (node) {head[x], y}; head[x] = cnt;}
void Dfs(int x, int fa) {
	Next(i, x) { int v = e[i].to;
		if(v == fa) continue; Dfs(v, x);
		f[x][1] += min(f[v][0], f[v][1]);
		f[x][0] += f[v][1];
	} f[x][1] += q[x];
}
void sfD(int x, int fa) {
	Next(i, x) { int v = read();
		if(v == fa) continue;
		ff[v][0] = ff[x][1] + f[x][1] - min(f[v][0], f[v][1]);
		ff[v][1] = min(ff[v][0], ff[x][0] + f[x][0] - f[v][1]);
		sfD(v, x);
	}
}
void baoli_dp(int q) {
	while(q --) { int a = read(), x = read(), b = read(), y = read(); mem(f, 0)
		f[a][x ^ 1] = f[b][y ^ 1] = inf; Dfs(1, 0);
		if(f[1][1] >= inf && f[1][0] >= inf) puts("-1"); else printf("%d\n", min(f[1][1], f[1][0]));
	}
}
void subtest1(int q) { f[1][0] = ff[1][0] = inf; Dfs(1, 0); sfD(1, 0);
	while(q --) { int a = read(), x = read(), b = read(), y = read();
		printf("%d\n", f[b][y] + ff[b][y]);
	}
}
signed main() { int n = read(), m = read(); cin >> s;
	Rep(i, 1, n) q[i] = read();
	Rep(i, 1, n - 1) x = read(), y = read(), Add(x, y), Add(y, x);
	if(n <= 2000 && m <= 2000) baoli_dp(m);
	else if(s[1] == '1') subtest1(m);
	return 0;
}

在考虑 \(*2\) 的情况，必然相邻的，那还是一样的，只考虑这 \(2\) 个取或不取。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#define maxn 100010
#define maxm 1000010
#define ls x << 1
#define rs x << 1 | 1
#define inf 10000000000
#define inc(i) (++ (i))
#define dec(i) (-- (i))
#define mid ((l + r) >> 1)
#define int long long
#define XRZ 212370440130137957
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
} string s; struct node { int nxt, to; } e[maxn << 1]; int head[maxn], dep[maxn], x, y, cnt, f[maxn][2], q[maxn], ff[maxn][2];
void Add(int x, int y) { e[inc(cnt)] = (node) {head[x], y}; head[x] = cnt;}
void Dfs(int x, int fa) {
	Next(i, x) { int v = e[i].to;
		if(v == fa) continue; Dfs(v, x); dep[v] = dep[x] + 1;
		f[x][1] += min(f[v][0], f[v][1]);
		f[x][0] += f[v][1];
	} f[x][1] += q[x];
}
void sfD(int x, int fa) {
	Next(i, x) { int v = read();
		if(v == fa) continue;
		ff[v][0] = ff[x][1] + f[x][1] - min(f[v][0], f[v][1]);
		ff[v][1] = min(ff[v][0], ff[x][0] + f[x][0] - f[v][1]);
		sfD(v, x);
	}
}
void baoli_dp(int q) {
	while(q --) { int a = read(), x = read(), b = read(), y = read(); mem(f, 0)
		f[a][x ^ 1] = f[b][y ^ 1] = inf; Dfs(1, 0);
		if(f[1][1] >= inf && f[1][0] >= inf) puts("-1"); else printf("%lld\n", min(f[1][1], f[1][0]));
	}
}
void subtest1(int q) { f[1][0] = ff[1][0] = inf; Dfs(1, 0); sfD(1, 0);
	while(q --) { int a = read(), x = read(), b = read(), y = read();
		printf("%lld\n", f[b][y] + ff[b][y]);
	}
}
void subtest2(int q) { Dfs(1, 0), sfD(1, 0);
	while(q --) { int x = read(), a = read(), y = read(), b = read();
		if(a == 0 && b == 0) { puts("-1"); continue;}
		if(dep[x] < dep[y]) swap(x, y), swap(a, b);
		printf("%lld", f[x][a] + ff[y][b] + (b == 1 ? f[y][1] - min(f[x][0], f[x][1]) : f[y][0] - f[x][1]));
	}
} 
signed main() { int n = read(), m = read(); cin >> s;
	Rep(i, 1, n) q[i] = read();
	Rep(i, 1, n - 1) x = read(), y = read(), Add(x, y), Add(y, x);
	if(n <= 2000 && m <= 2000) baoli_dp(m);
	else if(s[1] == '1') subtest1(m);
	else if(s[1] == '2') subtest2(m);
	return 0;
}

满分做法不会= =

知识点总结

部分分只要写还是蛮多的。考验选手做题经验，会不会死磕一题。

标签

\(DP\) 倍增 树剖

代码

见上。

Day2 总结

搞了好久，真的很毒瘤，做法完全不可做。

考场上估计 : \(60 + 65 + 44 = 169ps\)

\(T3\) 的暴力不可能拿满，但起码也有个 \(44ps\)

NOIP2018 总结

预计拿分 \(100 + 100 + 55 + 60 + 65 + 44\)

目前拿分 \(100 + 100 + 100 + 100 + 65 + 44\)

如果这场稍微炸了一题，也就凉了。。。

2019 年

Day1

T1 格雷码

题目大意

\(n + 1\) 位格雷码，由 \(n\) 位格雷码的 \(2^n\) 个二进制串按顺序排列再加前缀 \(0\)，和按逆序排列再加前缀 \(1\) 构成，共 \(2^{n + 1}\) 个二进制串。另外，对于 \(n\) 位格雷码中的 \(2^n\) 个二进制串，我们按上述算法得到的排列顺序将它们从 \(0 \sim 2^n - 1\) 编号。

求生成的 \(n\) 位格雷码中的第 \(k\) 位是什么。

题解

就是按照题意模拟就行了 直接递归实现。

或者是可以找规律可以发现第 \(k\) 位是 \(k \oplus \lfloor \frac{k}{2} \rfloor\)

知识点总结

还行吧

标签

递归， 数学

代码

递归版

#include<bits/stdc++.h>

using namespace std;

#define N 65
#define maxm 0
#define ls x << 1
#define rs x << 1 | 1
#define int unsigned long long
#define inf 0x3f3f3f3f
#define mid ((l + r) >> 1)
#define Rep(i, a, b) for(long long i = a; i <= b; ++ i)
#define Dep(i, a, b) for(int i = a; i >= b; -- i)
#define Next(i, u) for(int i = a; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);

int n, k, cnt, Pow[N] = {1}, Ans[N], a[3] = {0, 1};

int qpow(long long x, long long y) {
	return Pow[y];
	int ans = 1, base = x;
	while(y) {
		if(y & 1) ans *= base;
		base *= base; y /= 2;
	}
	return ans;
}

int find(long long x, long long y) {
	if(x == 1) return a[y];
	if(y >= qpow(2, x - 1)) return find(x - 1, qpow(2, x) - y - 1) + qpow(2, x - 1);
	else return find(x - 1, y);
}

void print(int x) {
	int now = x;
	if(x < 1) return ;
	print(x / 2);
	printf("%d", ((int) x) % 2);
}

signed main() {
	// file(code);
	scanf("%llu%llu", &n, &k); 
	Rep(i, 1, n) Pow[i] = Pow[i - 1] * 2;
	Dep(i, n, 1) {
		if(k >= Pow[i - 1]) Ans[i] = 1, k = Pow[i - 1] * 2 - 1 - k;
		else Ans[i] = 0;
	}
	Dep(i, n, 1) printf("%d", Ans[i]);
	return 0;
	scanf("%Lf%Lf", &n, &k);
	Pow[0] = 1;
	Rep(i, 1, n) Pow[i] = Pow[i - 1] * 2.0;
	while(++ cnt) if(qpow(2, cnt) > k) break;
	Rep(i, 1, n - cnt) printf("0");
	int ans = find(cnt, k);
	print(ans);
}

结论版

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#define maxn 50010
#define maxm 1000010
#define ls x << 1
#define rs x << 1 | 1
#define inf 10000000000
#define inc(i) (++ (i))
#define dec(i) (-- (i))
#define mid ((l + r) >> 1)
#define int long long
#define XRZ 212370440130137957
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
}
signed main() { int n = read(); unsigned long long k = read(); k ^= k >> 1;
    while(~-- n) cout << (k >> n & 1);
	return 0;
}

T2 括号树

题目大意

给定一棵有 \(n\) 个节点的树，每个节点对应一个括号（左或右），需要求出从该节点到根节点的简单路径所构成的括号串中合法括号子串的数量。

其中合法括号串的定义是这样的

()是合法括号串。

如果A是合法括号串，则(A)是合法括号串。

如果A，B是合法括号串，则AB是合法括号串。

其中 \(n ≤ 5 \times 10 ^ 5\)

题解

直接从父节点向子节点传递。

\(f[i] \to f[fa[i]] + 1\)

最后求答案的时候

\(sum[i] = sum[fa[x]] + f[i]\)

不过要用 \(stack\) 或其他 \(STL\) 维护一下。

不然会爆空间。

知识点总结

出的还不错吧，也比较草率。

标签

树形结构，dp

代码

\(100ps\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
const int N = 500010;
// const int M = 100010;
#define ls x << 1
#define rs x << 1 | 1
#define inf 0x3f3f3f3f
#define inc(i) (++ (i))
#define dec(i) (-- (i))
#define mid ((l + r) >> 1)
#define int long long
#define debug() puts("XRZ TXDY");
#define Next(i, u) for(int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
using namespace std;
char s[N];
int n, cnt, x, ans, flag, tot, num, head[N], f[N], Q[N], Val[N], fa[N], numm[N];
struct node {int to, nxt;}e[N << 1];
void Add(int u, int v) {e[++ cnt].to = v; e[cnt].nxt = head[u]; head[u] = cnt;}
// void Dfs(int x) {
// 	flag = 0; if(s[Q[tot]] == '(' && s[x] == ')') flag = Q[tot], dec(tot), inc(Val[Q[tot]]), f[x] += Val[Q[tot]]; else Q[++ tot] = x;
// 	Next(i, x) f[e[i].to] = f[x], Dfs(e[i].to);
// 	if(flag) dec(Val[Q[tot]]), Q[inc(tot)] = flag; else -- tot;
// }
void Dfs(int x) {
    int flag = 0;
    if(s[Q[tot]] == '(' && s[x] == ')') flag = Q[tot], dec(tot), inc(Val[Q[tot]]), f[x] += Val[Q[tot]]; else Q[inc(tot)] = x;
    Next(i, x) f[e[i].to] = f[x], Dfs(e[i].to);
    if(flag) dec(Val[Q[tot]]), Q[inc(tot)] = flag; else dec(tot);
}
signed main() {
	// file(a);
	scanf("%lld\n%s", &n, s + 1);
    Rep(i, 2, n) scanf("%lld", &x), Add(x, i); Dfs(1);
    Rep(i, 1, n) ans ^= i * f[i]; printf("%lld", ans); return 0;
	Rep(i, 2, n) {
		scanf("%lld", &x);
		if(x != i - 1) flag = 1;
		fa[i] = x;
	}
	if(flag == 0) {
		Rep(i, 1, n) {
			if(s[i] == '(' && s[i - 1] == ')') num = 1, f[i] = f[i - 1];
			else if(s[i] == '(' && s[i - 1] != ')') ++ num, f[i] = f[i - 1];
			else if(s[i] == ')' && num != 0) -- num, f[i] = f[i - 1] + 1;
			else if(s[i] == ')' && num == 0) f[i] = f[i - 1];
		}
	}
	else {
		if(s[1] == '(') numm[1] ++;
		Rep(i, 2, n) {
			if(s[i] == '(' && s[fa[i]] == ')') numm[i] = 1, f[i] = f[fa[i]];
			if(s[i] == '(' && s[fa[i]] != ')') numm[i] = numm[fa[i]] + 1, f[i] = f[fa[i]];
			if(s[i] == ')' && numm[fa[i]] != 0) numm[i] = numm[fa[i]] - 1, f[i] = f[fa[i]] + 1;
			if(s[i] == ')' && numm[fa[i]] == 0) f[i] = f[fa[i]];
		}
	}
	return 0;
}

T3 树上的数

题目大意

题解

不讲了吧（（（

不会写

10ps的暴力大概人均都会吧。

知识点总结

出的不好，完全没有区分度。

标签

树形结构（不知道）

代码

\(10ps\) 的写的太丑了就不放了。

Day1 总结

预计 \(100 + 100 + 10\)

实得 \(95 + 10 + 0\)

目前 \(100 + 100 + 10\)

Day2

T1 Emiya 家今天的饭

题目大意

题解

先考虑这题是满足 \(dp\) 的一些性质，无后效性等等

总之就是变着门子告诉你这题是 \(dp\) 。（一看题目就觉得很像 \(dp\)）

你现在需要求满足那 \(3\) 个条件的方案数，即：每行选不超过一个，且没有一列选了超过一半的食材的方案数。

那么这个东西其实是很不好求的，因为你要对每一列都要单独去判断，看他们是否超过一半，\(dp\) 不足以记下每一行的信息。

那么是不是可以考虑容斥一下，所求可以转化为：每行选不超过一个的方案数 - 每行选不超过一个，且某一列选了超过一半的方案数。

先枚举每一列 \(l\) 看不合法的组合方法有多少。

然后考虑，状态是什么：

令 \(f_{i,j,k}\) 表示，当前枚举到了第 \(i\) 行，第 \(l\) 列用过 \(j\) 份食材，到目前为止一共用了 \(k\) 份食材的方案数。

再考虑，怎么转移，令 \(s_i\) 表示第 \(i\) 行的总和：

\[f_{i, j, k} = f_{i - 1, j, k} + a_{i, l} \times f_{i - 1, j - 1, k} + (s_i - a_{i, l}) \times f_{i - 1, j, k - 1} \]

这样子的复杂度是 \(O(m * n ^ 3)\)

显然是过不了的，考虑 \(dp\) 优化三板斧（不是）

第一，剪去无用状态。

好像可以。。。。

因为你只需要对比 \(j\) 与 \(k\) 之间的大小关系，所以，可以把后 \(2\) 位压成一维，为 \(j\) 与 \(k\) 的差值。

转移也基本上是一样的：

\[f_{i, j} = f_{i - 1, j} + a_{i, l} \times f_{i - 1, j - 1} + (s_i - a_{i, l}) \times f_{i - 1, j + 1} \]

复杂度 \(O(m \times n ^ 2)\)

知识点总结

很妙的 \(dp\)。

标签

容斥，动态规划

代码

\(100ps\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#define maxn 110
#define maxm2010#define ls x << 1
#define rs x << 1 | 1
#define inf 10000000000
#define inc(i) (++ (i))
#define dec(i) (-- (i))
#define mid ((l + r) >> 1)
#define int long long
#define XRZ 998244353
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
} int a[maxn][maxm], Ans, tot[maxn][maxm << 1], f[maxn][maxm], s[maxn];
signed main() { int n = read(), m = read();
	Rep(i, 1, n) Rep(j, 1, m) a[i][j] = read(), s[i] = (s[i] + a[i][j]) % XRZ; tot[0][0] = 1;
	Rep(i, 1, n) Rep(j, 0, n) tot[i][j] = (tot[i - 1][j] + (j > 0 ? tot[i - 1][j - 1] * s[i] % XRZ : 0)) % XRZ;
	Rep(l, 1, m) { mem(f, 0); f[0][n] = 1;
		Rep(i, 1, n) Rep(j, n - i, n + i) f[i][j] = ((f[i - 1][j] + (f[i - 1][j - 1] * a[i][l] % XRZ)) % XRZ + f[i - 1][j + 1] * (s[i] - a[i][l] + XRZ) % XRZ) % XRZ;
		Rep(i, 1, n) Ans = (Ans + f[n][n + i]) % XRZ; 
	}  Rep(i, 1, n) Ans = (Ans - tot[n][i] + XRZ) % XRZ; printf("%d", Ans * (XRZ - 1) % XRZ);
	return 0;
}

T2 划分

题目大意

给你 \(n\) 个数，想让你把他划分成若干段，并且满足以下条件：

对于分界点 \(1 <= k_1 <= k_2 <= …… <= k_p <= n\) 使得 ：

\[(\sum_{i = 1} ^ {k_1}{a_i}) ^ 2 + (\sum_{i = k_1 + 1} ^ {k_2}{a_i}) ^ 2 + …… + (\sum_{i = k_{p - 1} + 1}^{k_p}{a_i}) ^ 2 \]

最小。

题解

考场上竟然写出了 \(64ps\) 的做法，虽然是猜的（至今还不会证）

那就讲下我的做法吧。

先考虑部分分：

\(1. n <= 10\) 和 \(n <= 50\) 的就不讲了。

\(2. n <= 400\) 这种做法是给 \(O(n^3)\) 的暴力 \(dp\)

具体怎么做的话是：

\[f_{j, k} = min(dp_{i, j} + (sum_k - sum_j) ^ 2) \]

\(3. n <= 5000\) 这个做法是给 \(O(n ^ 2)\) 的 \(dp\) 做的。

这里的话有 \(2\) 种做法。

第一种是优化上面那个式子，这种好像有个学长写了，就不多赘述。

第二种是和第一种完全不同的一种做法。

有个显而易见的做法（不是） ：维护每一段尽可能小，答案就会最优。

然后转移具有单调性的，所以用单调栈维护一下可以优化到 \(n^2\) 也就是正解的复杂度。

但是！ 还没完，这题要用高精 = =

这就离谱。

知识点总结

比较无厘头的一道题，比 \(T1\) 质量低很多。

给一些选手因为语言而造成优势。

标签

贪心，\(dp\)

代码

考场 \(64ps\) 代码

#include<bits/stdc++.h>

using namespace std;

#define maxn 500005
#define maxm 2001
#define ls x << 1
#define rs x << 1 | 1
#define int long long
const int inf = 5e18;
#define mid ((l + r) >> 1)
#define Rep(i, a, b) for(int i = a; i <= b; ++ i)
#define Dep(i, a, b) for(int i = a; i >= b; -- i)
#define Next(i, u) for(int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);

int n, Type, num[maxn], ans, f[maxn], sum[maxn], Que[maxn];

signed main() {
	file(partition);
	scanf("%lld%lld", &n, &Type);
	if(Type == 0) {
		Rep(i, 1, n) scanf("%lld", &num[i]), sum[i] = sum[i - 1] + num[i], f[i] = inf;
		if(n <= 5000) {
			f[0] = 0;
			Rep(i, 1, n) Rep(j, 0, i - 1) if(Que[j] <= sum[i] - sum[j] && f[i] > f[j] + (sum[i] - sum[j]) * (sum[i] - sum[j])) f[i] = f[j] + (sum[i] - sum[j]) * (sum[i] - sum[j]), Que[i] = sum[i] - sum[j];
			printf("%lld", f[n]);
		}
		else {
			Rep(i, 2, n) {
				if(num[i] >= num[i - 1]) {continue;}
				if(num[i + 1] > num[i - 1] || i == n) num[i] += num[i - 1], num[i - 1] = 0;
				else if(num[i + 1] < num[i - 1]) num[i + 1] += num[i], num[i] = num[i - 1], num[i - 1] = 0;
			}
			Rep(i, 1, n) if(num[i]) ans += num[i] * num[i];
			printf("%lld", ans); return 0;	
		}
	}
	return 0;
}

\(88ps\) 代码

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#define maxn 40000010
#define maxm 1000010
#define ls x << 1
#define rs x << 1 | 1
#define inf 10000000000
#define inc(i) (++ (i))
#define dec(i) (-- (i))
#define mid ((l + r) >> 1)
#define int long long
#define XRZ 212370440130137957
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
} int a[maxn], sum[maxn], num[maxn], q[maxn], f[maxn], l, r;
signed main() { int n = read(), type = read();
	Rep(i, 1, n) a[i] = read(), sum[i] = sum[i - 1] + a[i];
	Rep(i, 1, n) {
		while(l < r && num[q[l + 1]] + sum[q[l + 1]] <= sum[i]) inc(l);
		num[i] = sum[i] - sum[q[l]]; f[i] = f[q[l]] + num[i] * num[i];
		while(l < r && num[q[r]] + sum[q[r]] >= num[i] + sum[i]) dec(r); q[inc(r)] = i;
	} printf("%lld\n", f[n]);
	return 0;
}

T3 树的重心

题目大意

题解

只会暴力....

还有菊花图。

知识点总结

有点难，貌似是线段树合并之类的东西吧。

标签

树上结构

代码

只写了暴力的

\(40ps\)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cmath>
#define maxn 100010
#define maxm 1000010
#define ls x << 1
#define rs x << 1 | 1
#define inf 10000000
#define inc(i) (++ (i))
#define dec(i) (-- (i))
#define mid ((l + r) >> 1)
#define int long long
#define XRZ 212370440130137957
#define debug() puts("XRZ TXDY");
#define mem(i, x) memset(i, x, sizeof(i));
#define Next(i, u) for(register int i = head[u]; i ; i = e[i].nxt)
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout);
#define Rep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i <= i##Limit ; inc(i))
#define Dep(i, a, b) for(register int i = (a) , i##Limit = (b) ; i >= i##Limit ; dec(i))
int dx[10] = {1, -1, 0, 0};
int dy[10] = {0, 0, 1, -1};
using namespace std;
inline int read() {
    register int x = 0, f = 1; register char c = getchar();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
    return x * f;
}
struct Q { int Next, To;}
Edge[maxn]; int From[maxn], Sum_Edge, n, Rt, Size[maxn], Ans, Dp[maxn];
struct W { int x, y;} E[maxn]; int Sum_E; bool Cut[maxn];
inline void Add(const int &x , const int &y) { E[inc(Sum_E)] = (W){x, y};
	Edge[inc(Sum_Edge)] = (Q){ From[x], y}; From[x] = Sum_Edge;
	Edge[inc(Sum_Edge)] = (Q){ From[y], x}; From[y] = Sum_Edge;
}
inline void Dfs(const int &u , const int &f) { Size[u] = 1 ; 
	for(int e = From[u] ; e ; e = Edge[e].Next) if(!Cut[e]){
		int v = Edge[e].To ; if(v == f) continue ; 
		Dfs(v , u) ; Size[u] += Size[v] ; 
	}
}
inline void Get(const int &u , const int &f) { Dp[u] = Size[Rt] - Size[u] ; 
	for(int e = From[u] ; e ; e = Edge[e].Next) if(!Cut[e]){
		int v = Edge[e].To; if(v == f) continue;
		Dp[u] = max(Dp[u], Size[v]); Get(v , u);
	} if(Dp[u] < Ans) Ans = Dp[u];
}
signed main() {
	int t = read();
	while(t --) { int n = read(), Ot = 0, x, y; Sum_Edge = 1; Sum_E = 0;
	Rep(i, 1, n) From[i] = 0;
	Rep(i, 1, n - 1) x = read(), y = read(), Add(x, y);
	Rep(i, 1, n - 1) {
		int x = E[i].x, y = E[i].y ; Cut[i << 1] = Cut[i << 1 | 1] = 1 ; 
		Ans = inf; Rt = x; Dfs(x, 0); Get(x, 0);
		if(Ans == 0) Ot += x ;  else Rep(j, 1, n) if(Dp[j] == Ans) Ot += j ; 
		mem(Dp, 0) ; mem(Size, 0); Ans = inf; Rt = y; Dfs(y, 0); Get(y, 0);
		if(Ans == 0) Ot += y; else Rep(j, 1, n) if(Dp[j] == Ans) Ot += j ; 
		mem(Dp, 0); mem(Size, 0); Cut[i << 1] = Cut[i << 1 | 1] = 0;
	} printf("%d\n", Ot);
	} return 0;
}

Day2 总结

预计得法 \(32 + 84 + 40\)

实际得分 \(24 + 64 + 0\)

目前分数 \(100 + 84 + 40\)

NOIP2019 总结

预计得法 \(100 + 100 + 10 + 32 + 84 + 40\)

实际得分 \(85 + 10 + 0 + 24 + 64 + 0\)

目前分数 \(100 + 100 + 0 + 100 + 84 + 40\)

完结撒花！