数据结构与算法 之 排序算法的实现与优化(动画)
冒泡排序法
实现
- 对相邻的元素排序
- 若无数据交换,排序结束,如果存在执行步骤1
实际操作过程
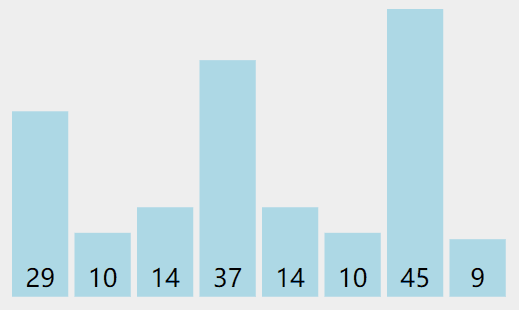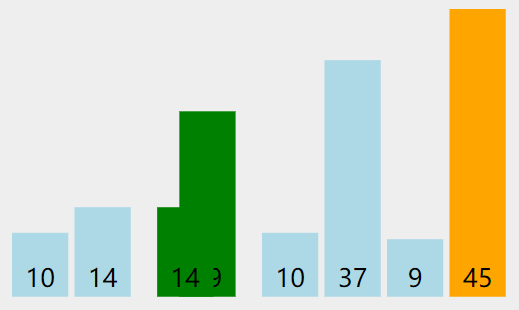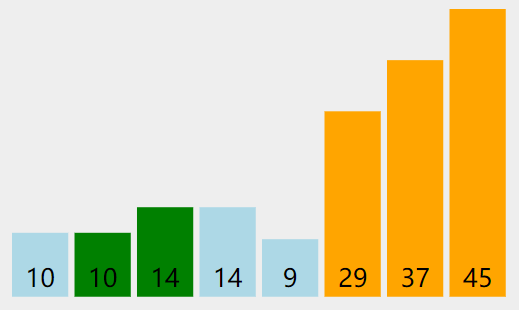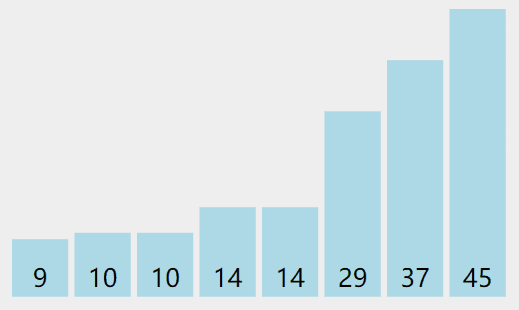
代码
template<typename T = double>
// 冒泡排序,arr 表示数组,n 表示数组大小
void bubbleSort(T arr[], int n) {
if (n <= 1) return;
for (int i = 0; i < n; ++i) {
// 提前退出冒泡循环的标志位
bool flag = false;
for (int j = 0; j < n - i - 1; ++j) {
if (arr[j] > arr[j+1]) { // 交换
std::swap(arr[j],arr[j+1])
flag = true; // 表示有数据交换
}
}
if (!flag) break; // 没有数据交换,提前退出
}
}
选择排序
实现
- 将整个数组作为排序区间
- 将排序区间的最小值(最大值)与起始元素交换
- 将排序段的起始位置后移一位,循环步骤2
实际操作过程
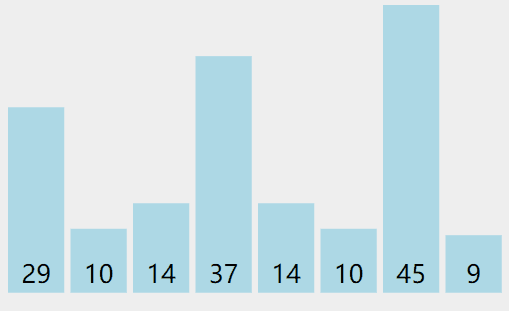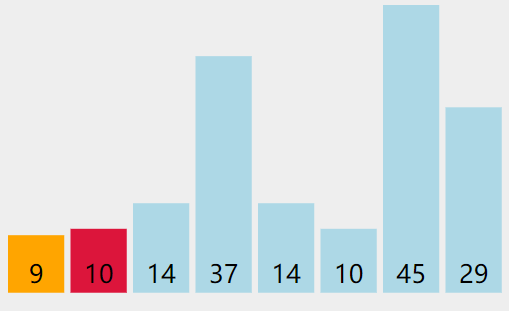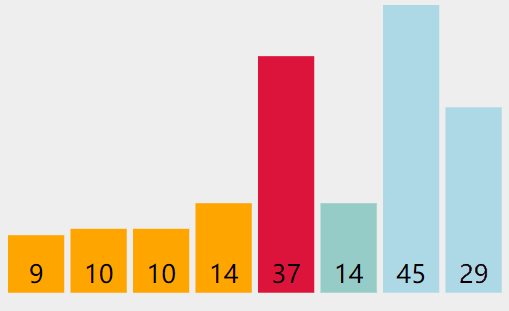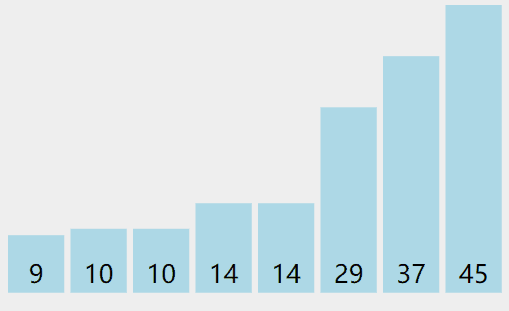
代码
template<typename T = double>
// 选择排序,arr 表示数组,n 表示数组大小
void selectionSort(T arr[], int n) {
for(int i = 0 ; i < n ; i ++) {
int minIndex = i;
for( int j = i + 1 ; j < n ; j ++ )
if( arr[j] < arr[minIndex] )
minIndex = j;
std::swap( arr[i] , arr[minIndex] );
}
}
插入排序
实现
- 将数组的[1:end]作为排序区间
- 将起始元素放在前段已排序数组的合理位置(大于前一个元素,小于后一个元素)。
- 将排序区间的起始位置后移一位,执行步骤2
优化
针对步骤2,将交换操作换为赋值操作
- 未优化前 当当前元素小于前一元素时,两者交换
- 优化后 保存当前元素,将大于该元素的区间元素整体后移,将当前元素保存至区间的首位
实际操作过程
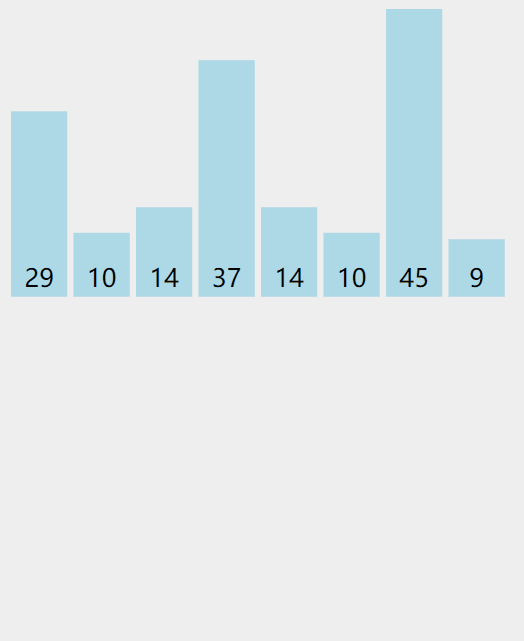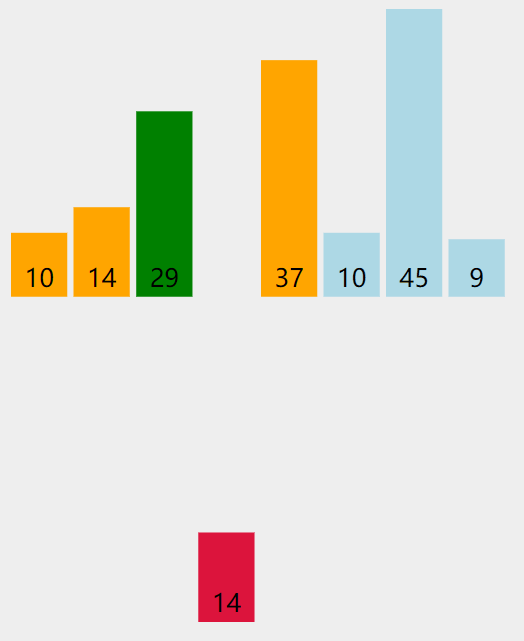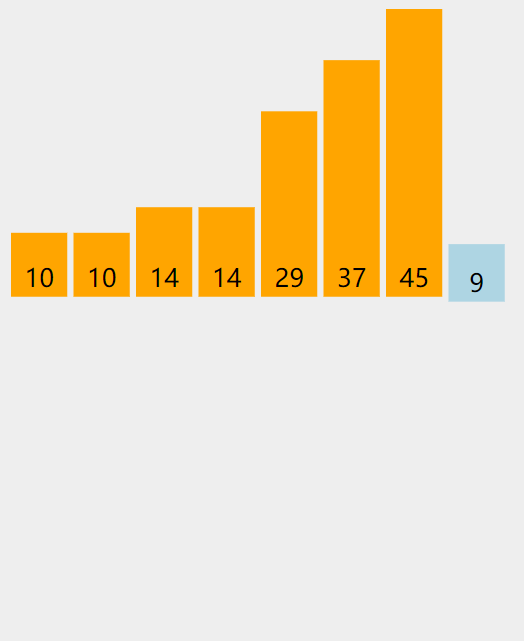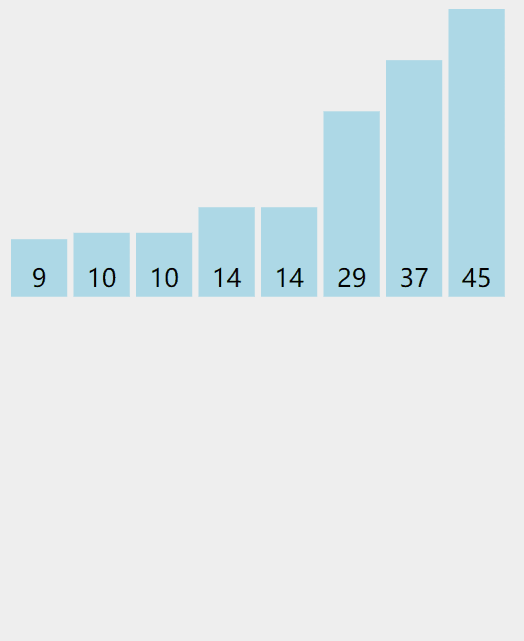
代码实现
template<typename T = double>
// 对arr[l...r]范围的数组进行插入排序
void _insertionSort(T arr[], int l, int r) {
for( int i = l+1 ; i <= r ; i ++ ) {
T e = arr[i];
int j;
for (j = i; j > l && arr[j-1] > e; j--)
arr[j] = arr[j-1];
arr[j] = e;
}
return;
}
归并排序
实现
- 将数组分为两段
- 对每段执行归并排序
- 对两段执行归并操作
优化
- 当两部分已经有序则无须merge。
- 当排序数组较小时,则使用插入排序进行排序。
实际操作过程
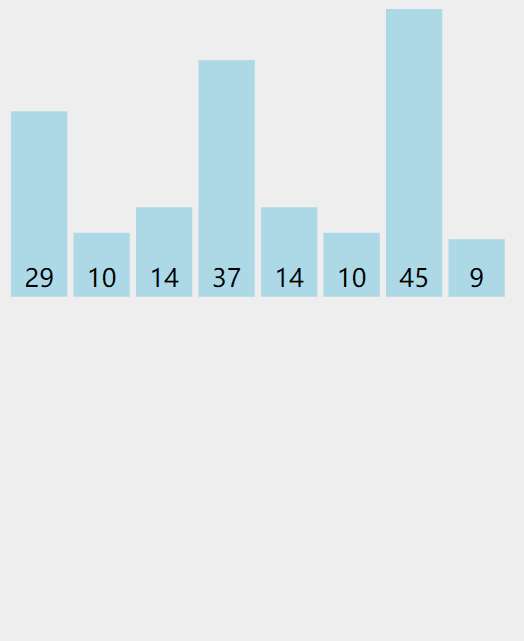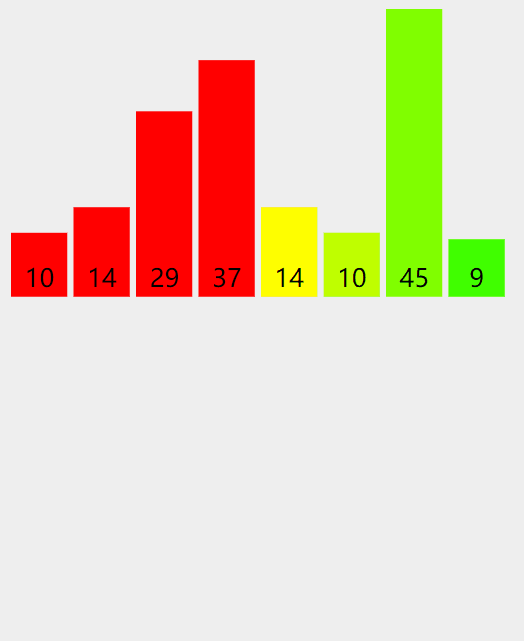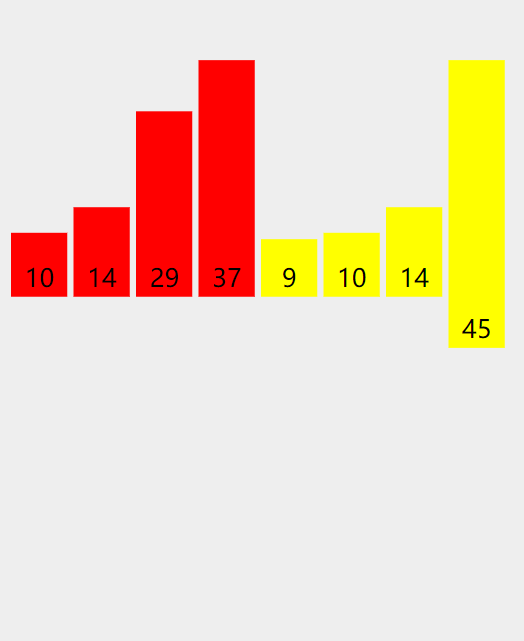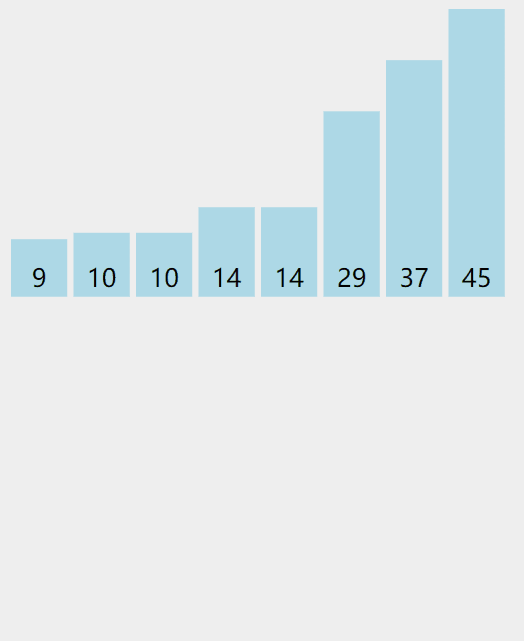
代码递归实现
template<typename T = double>
void __merge(T arr[], int l, int mid, int r) {
T aux[r-l+1];
for( int i = l ; i <= r; i ++ )
aux[i-l] = arr[i];
int i = l, j = mid+1;
for( int k = l ; k <= r; k ++ ) {
if( i > mid ) { arr[k] = aux[j-l]; j ++;} //保证 i 不越界
else if( j > r ){ arr[k] = aux[i-l]; i ++;} //保证 j 不越界
else if( aux[i-l] <= aux[j-l] ){ arr[k] = aux[i-l]; i ++;}
else { arr[k] = aux[j-l]; j ++;}
}
}
template<typename T = double>
void __mergeSort(T arr[], int l, int r) {
if( r - l <= 15 ){
_insertionSort(arr, l, r);
return;
}
int mid = (l+r)/2;
__mergeSort<T>(arr, l, mid); //排序
__mergeSort<T>(arr, mid+1, r); //排序
if( arr[mid] > arr[mid+1] )
__merge<T>(arr, l, mid, r); //归并
}
template<typename T = double>
void mergeSort(T arr[], int n) {
__mergeSort<T>( arr , 0 , n-1 );
}
代码循环实现
template <typename T>
void mergeSortBU(T arr[], int n) {
if( n <= 15 ){
_insertionSort(arr, 0, n-1);
return;
}
for(int sz = 1; sz <= n ; sz += sz)
for(int i = 0; i + sz < n ; i += sz + sz)
//对arr[i...i+sz-1]和arr[i+sz...i+2*sz-1]进行归并
if(arr[i + sz - 1] > arr[i + sz])
__merge( arr, i, i + sz - 1, std::min(i + sz + sz - 1, n - 1));
}
代码链表排序实现
由于归并排序的特殊性,所以非常适合链表这种数据结构的排序,所以在双向链表的归并排序C++实现(含注释,非递归)中具体进行了讲解双向链表的排序实现
快速排序
实现
- 起始元素作为分界元素v
- 认为剩下所有的元素均大于v,即[1,end]为大于v元素区间,从第二个元素向后扫描,当发现有小于v的元素,则将其与大于v元素区间的第一位进行交换
- 扫描完毕之后将,元素v即起始位置元素与小于v元素区间的首位进行交换。
- 对小于v元素区间和大于v元素区间分别执行步骤1
优化
- 针对近乎有序的数组:
- 随机取出一个元素v作为分界元素,与起始元素交换位置,当然不影响通常状态下的排序速度
- 认为
<v,>v区间均为空,从两端向中间搜索,将两端不符合条件的元素交换。
- 针对有较多重复键值的数组:
- 采取
quickSort 3 ways,将区间分为三部分,即<v,==v和>v。 认为三个区间均为空。 - 从两端向中间搜索,将小于v的元素与等于v的区间第一位元素交换,将大于v的元素,与大于v区间的前一位元素交换。
- 其中对于近乎有序且有较多重复键值的数组,与大于v区间的前一位元素交换前,先判断是否大于v,若大于v则,将区间起始位前移。
- 采取
- 在数组元素较少时选择插入排序进行排序
实际操作过程
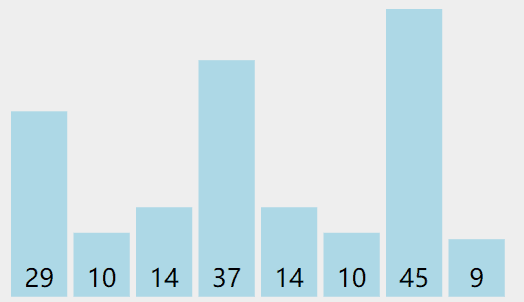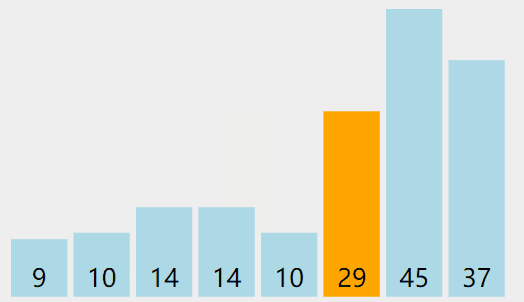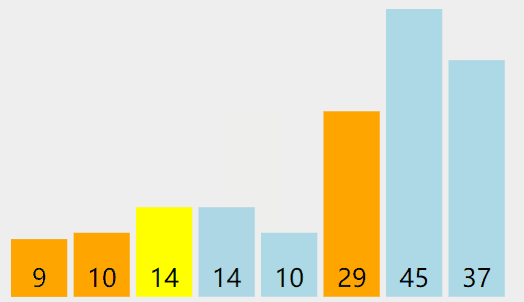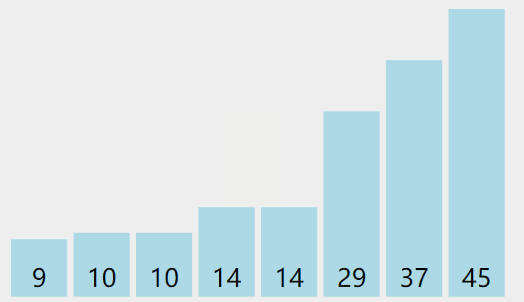
代码递归实现
template<typename T = double>
int _partition2(T arr[], int l, int r) {
std::swap<T>( arr[l] , arr[std::rand()%(r-l+1)+l] );
T v = arr[l];
int i = l+1, j = r;
while( true ){
while( i <= r && arr[i] < v )
i ++;
while( j >= l+1 && arr[j] > v )
j --;
if( i > j )
break;
std::swap<T>( arr[i] , arr[j] );
i ++;
j --;
}
std::swap<T>( arr[l] , arr[j]);
return j;
}
template<typename T = double>
void _quickSort(T arr[], int l, int r) {
if( r - l <= 15 ){
_insertionSort<T>(arr,l,r);
return;
}
int p = _partition2(arr, l, r);
_quickSort<T>(arr, l, p-1 );
_quickSort<T>(arr, p+1, r);
}
template<typename T = double>
void quickSort(T arr[], int n) {
std::srand(std::time(nullptr));
_quickSort<T>(arr, 0, n-1);
}
template <typename T>
void __quickSort3Ways(T arr[], int l, int r) {
if( r - l <= 15 ){
_insertionSort<T>(arr,l,r);
return;
}
std::swap( arr[l], arr[std::rand()%(r-l+1)+l ] );
T v = arr[l];
int lt = l; // arr[l+1...lt] < v
int gt = r + 1; // arr[gt...r] > v
int i = l+1; // arr[lt+1...i) == v
while( i < gt ){
if( arr[i] < v ){
std::swap( arr[i], arr[lt+1]);
i ++;
lt ++;
}
else if( arr[i] > v ){
while(arr[gt-1] > v && gt-1 != i)
gt --;
std::swap( arr[i], arr[--gt]);
}
else{ // arr[i] == v
i ++;
}
}
std::swap( arr[l] , arr[lt] );
__quickSort3Ways<T>(arr, l, lt-1);
__quickSort3Ways<T>(arr, gt, r);
}
template <typename T>
void quickSort3Ways(T arr[], int n) {
std::srand(std::time(nullptr));
__quickSort3Ways<T>( arr, 0, n-1);
}
C++标准库调用
在C++的标准库中已有排序算法的实现,在无特殊需求时,我们可以使用标准模板函数进行排序,常用的四个函数为std::sort、std::stable_sort、std::partial_sort、std::list::sort,其使用的是快速排序和归并排序进行实现的,调用方式如下为:
#include <algorithm>
#include <functional>
#include <array>
#include <iostream>
//用于链表打印
std::ostream& operator<<(std::ostream& ostr, const std::list<int>& list)
{
for (auto &i : list) {
ostr << " " << i;
}
return ostr;
}
int main()
{
std::array<int, 10> s = {5, 7, 4, 2, 8, 6, 1, 9, 0, 3};
// 用标准库比较函数对象进行快速排序
std::sort(s.begin(), s.end(), std::less<int>());
for (auto a : s) {
std::cout << a << " ";
}
std::cout << '\n';
s = std::array<int, 10>{5, 7, 4, 2, 8, 6, 1, 9, 0, 3};
// 用标准库比较函数对象进行部分快速排序
std::partial_sort(s.begin(), s.begin() + 3, s.end(), std::less<int>());
for (int a : s) {
std::cout << a << " ";
}
std::cout << '\n';
s = std::array<int, 10>{5, 7, 4, 2, 8, 6, 1, 9, 0, 3};
// 用标准库比较函数对象进行归并排序
std::stable_sort(s.begin(), s.end(), std::less<int>());
for (auto a : s) {
std::cout << a << " ";
}
std::cout << '\n';
std::list<int> list = { 8,7,5,9,0,1,3,2,6,4 };
// 用标准库比较函数对象进行链表的归并排序
list.sort(std::less<int>());
std::cout << list << "\n";
}
文章中GIF图片是使用网站https://visualgo.net/进行制作的
至此代码实现和优化过程已完成,具体的时间复杂度和排序特性将在博文各个常用的排序算法的适用场景详细分析(原地,稳定,最好、最坏、平均时间复杂度)中讲解。
任世事无常,勿忘初心



 浙公网安备 33010602011771号
浙公网安备 33010602011771号