二叉搜索树C++详细实现
相信大部分人都会实现二叉搜索树,实际上就是根据与当前节点相比的大与小进行整个树的建立。这里部分代码引用的是刘雨波老师的二叉搜索树代码,为了方便关于二叉搜索树其他内容的讲解,代码基本上具有注释,如果哪里写的不明白可以留言,因为我自己也修改了一下,不知道是否存在bug。
具体的功能有:
- 搜索元素
- 删除元素
- 插入元素
- 最大元素获取
- 最小元素获取
- 删除最大元素
- 删除最小元素
- 前、中、后、层序遍历
- 获取ceil值(大于所查找元素的全部元素中的最小元素)
- 获取floor值(小于所查找元素的全部元素中的最大元素)
- 获取元素的排名
- 查找排名第n个元素
下面针对常用功能进行讲解,由于搜索,删除以及插入元素的实现方法很简单,这里就不进行讲解了,具体的文字叙述在博文数据结构与算法之二叉查找树精简要点总结中已有提到,同时遍历方法在博文二叉搜索树的深度&广度优先遍历 C++实现中已经讲解了。
最大(小)值获取与删除
实际上由于二叉树的特性,由于中序遍历便是从小到大的排序,所以最大值和最小值均位于二叉树的最左端和最右端的叶子节点。这样我们只需要对一个节点进行操作,很简单就不多讲了。
获取ceil值
ceil值指的是大于所查找元素的全部元素中的最小元素,实现方法是保存搜索路径中最新的大于元素的值。下面进行该实现方法的分析。
搜索过程中当前节点的元素值与所查找元素一共有四种情况:
1. 当前节点元素小于所查找的元素,并且当前节点是父节点的右子节点
由于当前节点元素小于所查找元素,而我们需要的是大于等于所查找元素的节点,所以无需考虑当前节点。由于当前节点是父节点的右子节点,所以其大于父节点,所以父节点也小于所查找节点值。所以无需操作。
2. 当前节点元素小于所查找的元素,并且当前节点是父节点的左子节点
由于当前节点元素小于所查找元素,而我们需要的是大于等于所查找元素的节点,所以无需考虑当前节点。由于当前节点是父节点的左子节点,所以其小于父节点,所以父节点也大于所查找节点值。这时由于根据情况3,4已经保存了父节点的元素值。
3. 当前节点元素大于所查找的元素,并且当前节点是父节点的右子节点
由于当前节点元素大于所查找元素,所以保存当前节点的元素值。由于当前节点是父节点的右子节点,所以其大于父节点,所以所查找节点位于父节点的右子树,及所查找元素也大于父节点。所以这时应该保存当前节点元素值。
4. 当前节点元素大于所查找的元素,并且当前节点是父节点的左子节点
由于当前节点元素大于所查找元素,所以保存当前节点的元素值。由于当前节点是父节点的左子节点,所以其小于父节点,所以所查找节点位于父节点的左子树,及所查找元素也小于父节点。所以这时应该保存父节点元素值。
不知道看到这里读者是否已经看懂了这个实现方法的可行性,但是有一点没有考虑到,就是说不在搜索路径中的节点是否也可能是ceil值呢,现在我们再来分析一下,实际情况也分为两种:
1. 当前节点元素大于所查找的元素
这时下一步将进行,即左子树的查找,同时由于当前元素值大于所查找的元素值,所以当前元素值的小于于右子树的全部节点元素值。所以有以下的关系式。
所以右子树不需要遍历。
2. 当前节点元素小于所查找的元素
这时下一步将进行,即右子树的查找,同时由于当前元素值大于所查找的元素值,所以当前元素值的大于左子树的全部节点元素值。所以左子树也不需要遍历
所以可以看出每次我们保存的都是搜索路径中的最新大于所查找元素的节点元素值(有点绕,多担待😁),同时我们保证每一个搜索到的元素都按照这样的步骤进行操作便可以实现ceil元素的获取了,可见我们的实现方法是正确的
代码实现如下
Key ceil(Key key) {
return ceil(root, key);
}
Key ceil(Node *node, Key key) {
Node *ceilNode = nullptr;
while (true) {
if (node == nullptr)
break;
if (key == node->key)
break;
else if (key < node->key) {
ceilNode = node;
node = node->left;
} else {
node = node->right;
}
}
return ceilNode == nullptr ? -1 : ceilNode->key;
}
获取floor值
floor值指的是小于所查找元素的全部元素中的最大元素,实现方法是保存搜索路径中最新的小于元素的值。下面进行该实现方法的分析。
搜索过程中当前节点的元素值与所查找元素一共有也四种情况:
- 当前节点元素小于所查找的元素,并且当前元素是父节点的右子节点
- 当前节点元素小于所查找的元素,并且当前元素是父节点的左子节点
- 当前节点元素大于所查找的元素,并且当前元素是父节点的右子节点
- 当前节点元素大于所查找的元素,并且当前元素是父节点的左子节点
由于这四种情况与ceil值获取原理类似便不再讲解。
代码实现如下
Key floor(Key key) {
return floor(root, key);
}
Key floor(Node *node, Key key) {
Node *floorNode = nullptr;
while (true) {
if (node == nullptr)
break;
if (key == node->key)
break;
else if (key < node->key) {
node = node->left;
} else {
floorNode = node;
node = node->right;
}
}
return floorNode == nullptr ? -1 : floorNode->key;
}
查找排名第n的元素
对于正在刷题的同学,肯定做过获取第n个元素这个算法,是通过中序遍历获取的,这里提供另一种思路,在二叉树中为每一个节点添加count变量,存储当前节点下全部节点的个数(包括本身)。如下图所示:
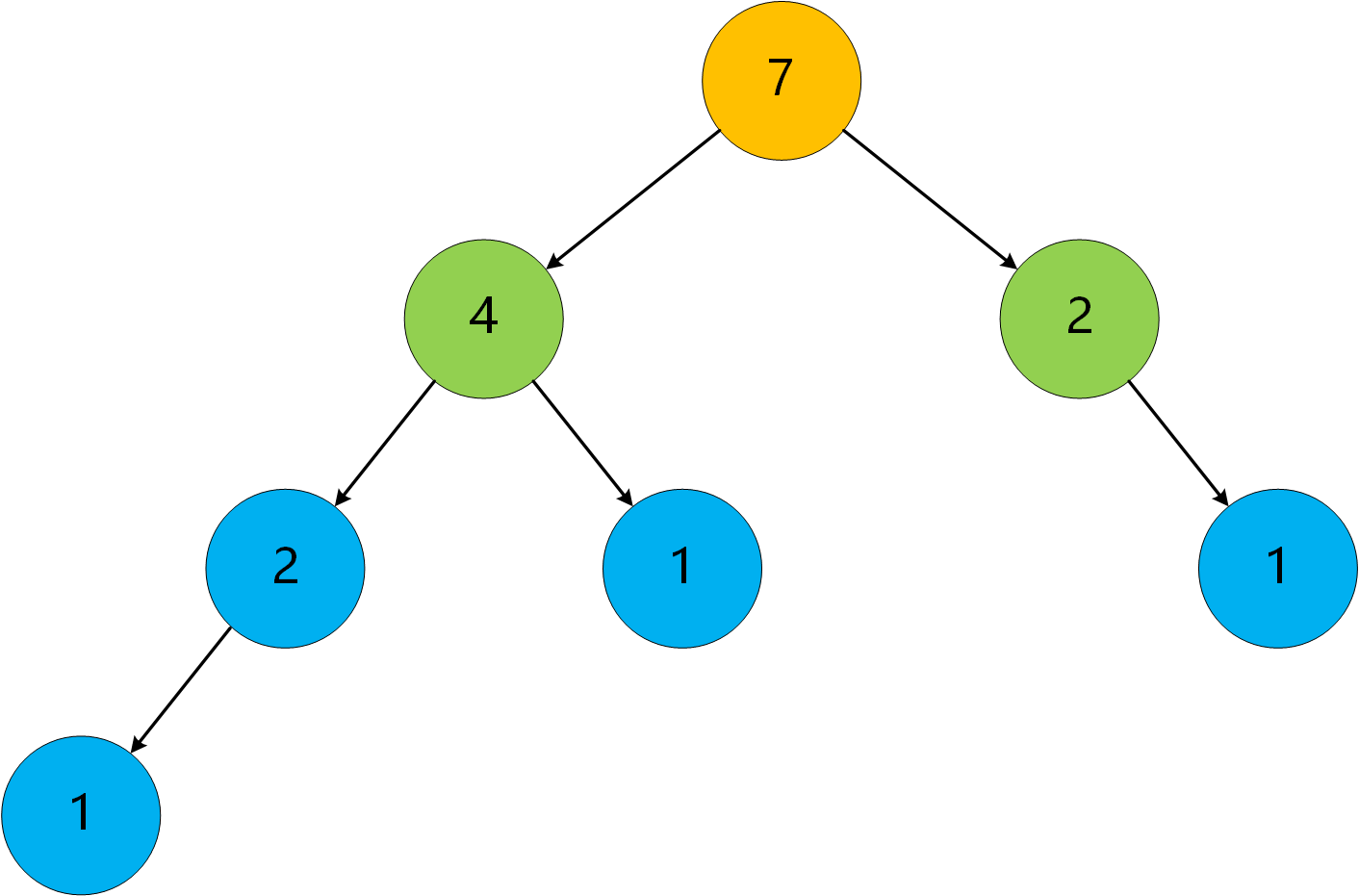
通过维护该树中所含元素的个数count可以求得,其与查找元素相似,在查找过程中,令当大于当前节点元素时,执行rank -= 该节点左子树的节点个数+1,当rank=该节点左子树的节点个数+1时,当前节点为所求节点;
实际上这分为三种情况,我来简单分析一下:
1. 当前节点左子节点的Count(左子树的节点数)大于当前的Rank值 - 1
由于左子树的Count值大于当前的Rank值 - 1,所以左子树包含的元素多于Rank值 - 1,而当前值大于左子树所有节点,即当前值的排名大于Rank,所以应该想左子树搜索。
2. 当前节点左子节点的Count(左子树的节点数)小于当前的Rank值 - 1
由于左子树的Count值小于当前的Rank值 - 1,所以左子树包含的元素小于Rank值 - 1,而当前值大于左子树所有节点,即当前值的排名小于Rank,所以应该向右子树搜索。
3. 当前节点左子节点的Count(左子树的节点数)等于当前的Rank值 - 1
由于左子树的Count值小于当前的Rank值 - 1,所以左子树包含的元素等于Rank值 - 1,而当前值大于左子树所有节点,即当前值的排名等于Rank,所以当前节点为所需节点。
代码实现如下
Value *select(int rank) {
return select(root, rank);
}
Value *select(Node *node, int rank) {
if (rank <= 0)
return nullptr;
while (true) {
if (node == nullptr)
return nullptr;
if (rank == (node->left != nullptr ? node->left->count + 1 : 1))
return &node->value;
else {
if (rank < (node->left != nullptr ? node->left->count + 1 : 1)) {
node = node->left;
} else {
rank -= (node->left != nullptr ? node->left->count + 1 : 1);
node = node->right;
}
}
}
}
查找元素的排名rank
通过维护该树中所含元素的个数n可以求得,其与查找元素相似,在查找过程中,令当大于等于当前节点元素时执行 rank += 该节点左子树的节点个数+1,即可求得rank;因为如果是搜索右子树时,则在原来的rank基础上又增加了左子树全部节点的个数。这里的分析和查找排名第n的元素类似,便不详细展开了。
代码实现如下
int rank(Key key) {
return rank(root, key);
}
int rank(Node *node, Key key) {
int _rank = 0;
while (true) {
if (node == nullptr)
return -1;
if (key == node->key) {
_rank += node->right != nullptr ? node->count - node->right->count : node->count;
return _rank;
} else {
if (key < node->key) {
node = node->left;
} else {
_rank += node->right != nullptr ? node->count - node->right->count : node->count;
node = node->right;
}
}
}
}
二叉树的完整代码
template<typename Key, typename Value>
class binarySearchTree {
private:
struct Node {
Key key;
Value value;
int count;
Node *left;
Node *right;
Node(Key key, Value value) {
this->key = key;
this->value = value;
this->count = 1;
this->left = this->right = nullptr;
}
Node(Node *node) {
this->key = node->key;
this->value = node->value;
this->count = node->count;
this->left = node->left;
this->right = node->right;
}
};
Node *root;
int count;
public:
binarySearchTree() {
root = nullptr;
count = 0;
}
~binarySearchTree() {
destroy(root);
assert(count == 0);
}
// 返回二叉树的元素个数
int size() {
return count;
}
// 返回二叉树是否为空
int isEmpty() {
return count == 0;
}
// 插入节点
void insert(Key key, Value value) {
if (!this->contain(key)) {
if (root == nullptr) {
root = new Node(key, value);
count++;
return;
}
root->count++;
insert(root, key, value);
}
}
// 检查二叉树是否包含键值为key的元素
bool contain(Key key) {
return contain(root, key);
}
// 在二叉树中寻找键值为key的value值
Value *search(Key key) {
return search(root, key);
}
// 前序遍历
void preOrder() {
preOrder(root);
}
// 中序遍历
void inOrder() {
inOrder(root);
}
// 后序遍历
void postOrder() {
postOrder(root);
}
// 层序遍历
void levelOrder() {
std::queue<Node *> q;
q.push(root);
while (!q.empty()) {
Node *node = q.front();
q.pop();
std::cout << node->key << " ";
if (node->left)
q.push(node->left);
if (node->right)
q.push(node->right);
}
}
// 寻找最小的键值
Key minimum() {
assert(count != 0);
Node *minNode = minimum(root);
return minNode->key;
}
// 寻找最大的键值
Key maximum() {
assert(count != 0);
Node *maxNode = maximum(root);
return maxNode->key;
}
// 从二叉树中删除最小值所在节点
void removeMin() {
if (root)
root = removeMin(root);
}
// 从二叉树中删除最大值所在节点
void removeMax() {
if (root)
root = removeMax(root);
}
// 从二叉树中删除键值为key的节点
void remove(Key key) {
root = remove(root, key);
}
Key floor(Key key) {
return floor(root, key);
}
Key ceil(Key key) {
return ceil(root, key);
}
int rank(Key key) {
return rank(root, key);
}
int getCount(Key key) {
return getCount(root, key);
}
Value *select(int rank) {
return select(root, rank);
}
private:
// 在以node为根的二叉搜索树中查找key所对应的value
Value *search(Node *node, Key key) {
while (true) {
if (node == nullptr)
return nullptr;
if (key == node->key)
return &(node->value);
else if (key < node->key)
node = node->left;
else
node = node->right;
}
}
Key floor(Node *node, Key key) {
Node *floorNode = nullptr;
while (true) {
if (node == nullptr)
break;
if (key == node->key)
break;
else if (key < node->key) {
node = node->left;
} else {
floorNode = node;
node = node->right;
}
}
return floorNode == nullptr ? -1 : floorNode->key;
}
Key ceil(Node *node, Key key) {
Node *ceilNode = nullptr;
while (true) {
if (node == nullptr)
break;
if (key == node->key)
break;
else if (key < node->key) {
ceilNode = node;
node = node->left;
} else {
node = node->right;
}
}
return ceilNode == nullptr ? -1 : ceilNode->key;
}
int rank(Node *node, Key key) {
int _rank = 0;
while (true) {
if (node == nullptr)
return -1;
if (key == node->key) {
_rank += node->right != nullptr ? node->count - node->right->count : node->count;
return _rank;
} else {
if (key < node->key) {
node = node->left;
} else {
_rank += node->right != nullptr ? node->count - node->right->count : node->count;
node = node->right;
}
}
}
}
Value *select(Node *node, int rank) {
if (rank <= 0)
return nullptr;
while (true) {
if (node == nullptr)
return nullptr;
if (rank == (node->left != nullptr ? node->left->count + 1 : 1))
return &node->value;
else {
if (rank < (node->left != nullptr ? node->left->count + 1 : 1)) {
node = node->left;
} else {
rank -= (node->left != nullptr ? node->left->count + 1 : 1);
node = node->right;
}
}
}
}
// 向以node为根的二叉搜索树中,插入节点(key, value)
// 返回插入新节点后的二叉搜索树的根
void insert(Node *node, Key key, Value value) {
while (true) {
if (key == node->key) {
node->value = value;
return;
} else {
if (key < node->key) {
if (node->left != nullptr) {
node = node->left;
node->count += 1;
} else {
node->left = new Node(key, value);
count++;
return;
}
} else {// key > node->key
if (node->right != nullptr) {
node = node->right;
node->count += 1;
} else {
node->right = new Node(key, value);
count++;
return;
}
}
}
}
}
// 查看以node为根的二叉搜索树中是否包含键值为key的节点
bool contain(Node *node, Key key) {
while (true) {
if (node == nullptr)
return false;
if (key == node->key)
return true;
else if (key < node->key)
node = node->left;
else
node = node->right;
}
}
// 查看以node为根的二叉搜索树中key节点的count
int getCount(Node *node, Key key) {
while (true) {
if (node == nullptr)
return -1;
if (key == node->key)
return node->count;
else if (key < node->key)
node = node->left;
else
node = node->right;
}
}
// 对以node为根的二叉搜索树进行前序遍历
void preOrder(Node *node) {
if (node != nullptr) {
std::cout << node->key << " ";
preOrder(node->left);
preOrder(node->right);
}
}
// 对以node为根的二叉搜索树进行中序遍历
void inOrder(Node *node) {
if (node != nullptr) {
inOrder(node->left);
std::cout << node->key << " ";
inOrder(node->right);
}
}
// 对以node为根的二叉搜索树进行后序遍历
void postOrder(Node *node) {
if (node != nullptr) {
postOrder(node->left);
postOrder(node->right);
std::cout << node->key << " ";
}
}
void destroy(Node *node) {
if (node != nullptr) {
destroy(node->left);
destroy(node->right);
delete node;
count--;
}
}
// 在以node为根的二叉搜索树中,返回最小键值的节点
Node *minimum(Node *node) {
if (node->left == nullptr)
return node;
return minimum(node->left);
}
// 在以node为根的二叉搜索树中,返回最大键值的节点
Node *maximum(Node *node) {
if (node->right == nullptr)
return node;
return maximum(node->right);
}
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
Node *removeMin(Node *node) {
if (node->left == nullptr) {
Node *rightNode = node->right;
delete node;
count--;
return rightNode;
}
node->left->count--;
node->left = removeMin(node->left);
return node;
}
// 删除掉以node为根的二分搜索树中的最大节点
// 返回删除节点后新的二分搜索树的根
Node *removeMax(Node *node) {
if (node->right == nullptr) {
Node *leftNode = node->left;
delete node;
count--;
return leftNode;
}
node->right->count--;
node->right = removeMax(node->right);
return node;
}
// 删除掉以node为根的二分搜索树中键值为key的节点
// 返回删除节点后新的二分搜索树的根
Node *remove(Node *node, Key key) {
if (node == nullptr)
return nullptr;
if (key < node->key) {
node->left->count--;
node->left = remove(node->left, key);
return node;
} else if (key > node->key) {
node->right->count--;
node->right = remove(node->right, key);
return node;
} else { // key == node->key
if (node->left == nullptr) {
Node *rightNode = node->right;
delete node;
count--;
return rightNode;
}
if (node->right == nullptr) {
Node *leftNode = node->left;
delete node;
count--;
return leftNode;
}
assert(node->left != nullptr && node->right != nullptr);
Node *successor = new Node(minimum(node->right));
count++;
successor->count = node->count--;
successor->right = removeMin(node->right);
successor->left = node->left;
delete node;
count--;
return successor;
}
}
};



 浙公网安备 33010602011771号
浙公网安备 33010602011771号