线性回归(Linear Regression)
理论实现
最简单的想法是
\[y \approx \sum _ { i = 0 } ^ { d } w _ { i } x _ { i }
\]
线性回归的假设函数为: \(h(\mathrm{x}) = \mathrm{w}^{T} \mathrm{x}\)。类似于 perceptron 只是没有 sign 函数。
线性回归的目的是找到一个方差最小的超平面(线条),所以误差检测使用流行的方差(squared error)
\[\operatorname{err}(\tilde{y}, y) =(\tilde{y}-y)^{2}
\]
in-sample / out-of-sample 误差为:
\[E _ { \mathrm { in } } ( \mathbf { w } ) = \frac { 1 } { N } \sum _ { n = 1 } ^ { N } ( \underbrace { h \left( \mathbf { x } _ { n } \right) } _ { \mathbf { w } ^ { T } \mathbf { x } _ { n } } - y _ { n } ) ^ { 2 }\\
E _ { \text {out } } ( \mathbf { w } ) = \underset { ( \mathbf { x } , y ) \sim P } { \mathcal { E } } \left( \mathbf { w } ^ { T } \mathbf { x } - y \right) ^ { 2 }
\]
为了表示方便写出 in-sample 误差 \(E _ { \mathrm { in } } ( \mathbf { w } )\) 的矩阵形式:
\[\begin{aligned} E _ { \mathrm { in } } ( \mathbf { w } )
& = \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \left( \mathbf { w } ^ { T } \mathbf { x } _ { n } - y _ { n } \right) ^ { 2 } = \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \left( \mathbf { x } _ { n } ^ { T } \mathbf { w } - y _ { n } \right) ^ { 2 } \\
&= \frac { 1 } { N } \left\| \begin{array} { c } \mathbf { x } _ { 1 } ^ { T } \mathbf { w } - y _ { 1 } \\ \mathbf { x } _ { 2 } ^ { T } \mathbf { w } - y _ { 2 } \\ \cdots \\ \mathbf { x } _ { N } ^ { T } \mathbf { w } - y _ { N } \end{array} \right\| ^ { 2 }\\
&= \frac { 1 } { N } \left\| \left[ \begin{array} { c } - - \mathbf { x } _ { 1 } ^ { T } - - \\ - - \mathbf { x } _ { 2 } ^ { T } - - \\ \cdots \\ - - \mathbf { x } _ { N } ^ { T } - - \end{array} \right] \mathbf { w } - \left[ \begin{array} { c } y _ { 1 } \\ y _ { 2 } \\ \cdots \\ y _ { N } \end{array} \right] \right\| ^ { 2 }\\
& = \frac { 1 } { N } \| \underbrace { X } _ { N \times d + 1 } \underbrace { \mathbf { w } } _ { d + 1 \times 1 } - \underbrace { \mathbf { y } } _ { N \times 1 } \| ^ { 2 }
\end{aligned}
\]
那现在的任务便是
\[\min _ { w } E _ { i n } ( \mathbf { w } ) = \frac { 1 } { N } \| X \mathbf { w } - \mathbf { y } \| ^ { 2 }
\]
此时的 \(E _ { \mathrm { in } } ( \mathbf { w } )\) 曲线如下:
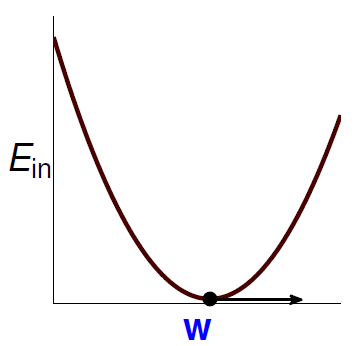
由公式和图形可知 \(E _ { \mathrm { in } } ( \mathbf { w } )\) 是连续(continuous),可微(differentiable),凸(convex)的。那么最小化 \(E _ { \mathrm { in } } ( \mathbf { w } )\) 的必要条件(necessary condition)是:
\[\nabla E _ { \text {in } } ( \mathbf { w } ) \equiv \left[ \begin{array} { c } \frac { \partial E _ { \text {in } } } { \partial w _ { 0 } } ( \mathbf { w } ) \\ \frac { \partial E _ { \text {in } } } { \partial w _ { 1 } } ( \mathbf { w } ) \\ \cdots \\ \frac { \partial E _ { \text {in } } } { \partial w _ { d } } ( \mathbf { w } ) \end{array} \right] = \left[ \begin{array} { c } 0\\ 0\\ \cdots\\ 0\\ \end{array} \right]
\]
那么现在的任务便是找出\(\mathbf{w}_{LIN}\) 使得 \(\nabla E _ { \text {in } }(\mathbf{w}_{LIN}) = 0\)。
矩阵形式的多项式展开为:
\[E _ { \mathrm { in } } ( \mathbf { w } ) = \frac { 1 } { N } \| \mathrm { Xw } - \mathbf { y } \| ^ { 2 } = \frac { 1 } { N } \left( \mathbf { w } ^ { T } \mathbf { X } ^ { T } \mathbf { X } \mathbf { w } - 2 \mathbf { w } ^ { T } \mathbf { X } ^ { T } \mathbf { y } + \mathbf { y } ^ { T } \mathbf { y } \right)
\]
所以其矩阵求导结果为(可类比于非向量形式):
\[\nabla E _ { \text {in } } ( \mathbf { w } ) = \frac { 2 } { N } \left( X ^ { T } X \mathbf { w } - X ^ { T } \mathbf { y } \right)
\]
那么现在令其为零可求得:
\[\mathbf { w } _ { \mathrm { LIN } } = \mathrm { X } ^ { \dagger } \mathbf { y }
\]
其中 \({ \dagger }\) 代表伪逆,当\(\mathrm { X }^{T} \mathrm { X }\)非奇异时也可使用 \(\mathbf { w } _ { \mathrm { LIN } } = (\mathrm { X }^{T} \mathrm { X })^{-1} \mathrm { X } \mathbf { y }\) 求得。
总结一下Linear Regression算法的实现步骤为:
- 通过数据集,获取输入矩阵(input matrix)和输出向量(output vector)
\[X = \underbrace{\left[ \begin{array} { c } - - \mathbf { x } _ { 1 } ^ { T } - - \\ - - \mathbf { x } _ { 2 } ^ { T } - - \\ \cdots \\ - - \mathbf { x } _ { N } ^ { T } - - \end{array} \right]}_{N \times (d+1)} \,\,\,\,\,\,\,\,\,\, \mathbf{y} = \underbrace{\left[ \begin{array} { c } y _ { 1 } \\ y _ { 2 } \\ \cdots \\ y _ { N } \end{array} \right]}_{N \times 1} \\
\]
- 计算伪逆 (pseudo-inverse)\(\underbrace{\mathrm { X } ^ { \dagger }}_{(d+1) \times N}\)
- return \(\underbrace{\mathbf { w } _ { \mathrm { LIN } }}_{d+1 \times 1} = \mathrm { X } ^ { \dagger } \mathbf { y }\)
Hat Matrix 的几何视角
下面公式的意义为对于服从统一分布的数据,经过多次抽取后训练误差的平均 \(\overline{E _ { \text {in } }}\),而其大概长下面这个样子是
\[\overline{E _ { \text {in } }} = \underset { \mathcal { D } _ { \sim P N } } { \mathcal { E } } \left\{ E _ { \text {in } } \left( \mathbf { w } _ { \text {LIN } } \text { w.r.t. } \mathcal { D } \right) \right\} = \text{noise level} \cdot \left( 1 - \frac { d + 1 } { N } \right)
\]
\[\begin{aligned}
E _ { \mathrm { in } } \left( \mathbf { w } _ { \mathrm { LIN } } \right) = \frac { 1 } { N } \| \mathbf { y } - \underbrace { \hat { \mathbf { y } } } _ { \text {predictions } } \| ^ { 2 }
& = \frac { 1 } { N } \| \mathbf { y } - \mathrm { X } \underbrace { \mathrm { X } ^ { \dagger } \mathbf { y } } _ { \mathrm { W } _ { \mathrm { LIN } } } \| ^ { 2 }\\
& = \frac { 1 } { N } \| (\underbrace{\mathbf { I }}_{\text{identity}} - \mathrm { X } \underbrace { \mathrm { X } ^ { \dagger }) \mathbf { y } } _ { \mathrm { W } _ { \mathrm { LIN } } } \| ^ { 2 }
\end{aligned}
\]
这里叫 \(\mathrm { X } \mathrm { X } ^ {\dagger}\) 为 hat matrix \(H\)。
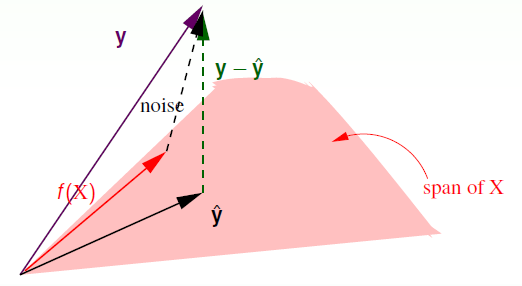
经过上述推导,可以得出 \(\hat {\mathbf { y } }= \mathrm { X }\mathbf { w } _ { \mathrm { LIN } }\) ,即 \(\hat {\mathbf { y } }\) 是 \(\mathbf{x}_{n}\) 的线性组合,也是由 \(\mathbf{x}_{n}\) 展开的空间中的一个向量;同时由于 \(\mathbf { y }\) 是独立于该空间外的一个向量,同时由于 \(\mathbf { y }-\hat {\mathbf { y } }\) 最小,那么 \(\mathbf { y }-\hat {\mathbf { y } }\) 必然垂直于该空间。进而可以得出 \(\hat {\mathbf { y } }\) 是 \(\mathbf { y }\) 在该空间上的一个投影,而投影矩阵便是 \(H\)。所以 \(I - H\) 也可以看作 \(\mathbf { y }\) 向 \(\mathbf { y }-\hat {\mathbf { y } }\) 映射的投影矩阵。
可以推导得 \(\text{trace}(I - H) = N - (d + 1)\),不详细解释。物理意义是将一个\(N\)维向量向\(d+1\)维空间做投影时,其余数的自由度最多有只有\(N - (d + 1)\)。
那么 noise 向量向该空间内投影后取余仍然是 \(( \mathbf { I } - \mathrm { H } )\text{noise} = \mathbf { y }-\hat {\mathbf { y } }\) ,即:
\[\begin{aligned} E _ { \text {in } } \left( \mathbf { w } _ { \mathrm { LIN } } \right) = \frac { 1 } { N } \| \mathbf { y } - \hat { \mathbf { y } } \| ^ { 2 } & = \frac { 1 } { N } \| ( \mathbf { I } - \mathrm { H } ) \text { noise } \| ^ { 2 } \\
& = \frac { 1 } { N } ( N - ( d + 1 ) ) {\| \text{noise} \|} ^ { 2 } \\
& = \frac { 1 } { N } ( N - ( d + 1 ) ) \sigma ^ { 2 }
\end{aligned}
\]
经过理论推导可以得出(这里不详细推导):
\[\begin{aligned}
\overline{E _ { \text {in} }} &= ( 1 - \frac { d + 1 } { N } ) \sigma ^ { 2 } \\
\overline{E _ { \text {out} }} &= ( 1 + \frac { d + 1 } { N } ) \sigma ^ { 2 }
\end{aligned}
\]
将两者绘制出随数据量增加的变化曲线如下:
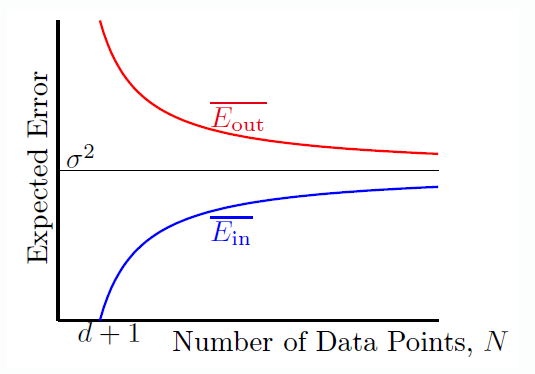
可以看出当 \(N \rightarrow \inf\) 时,两者均收敛,且两者之差为 \(\frac { 2(d + 1) } { N }\)。类似于 VC bound。
线性回归(Linear Regression)\(\rightarrow\)分类(Classification)
由于 Linear Classification 是一种 NP-Hard 问题,那可以将回归的解决方法用于分类吗?
先对比一下两者的误差测量函数:
\[\operatorname { err } _ { 0 / 1 } = \left\| \operatorname { sign } \left( \mathbf { w } ^ { T } \mathbf { x } \right) \neq y \right\| \quad \text { err } _ { \mathrm { sqr } } = \left( \mathbf { w } ^ { T } \mathbf { x } - y \right) ^ { 2 }
\]
绘制出曲线如下:
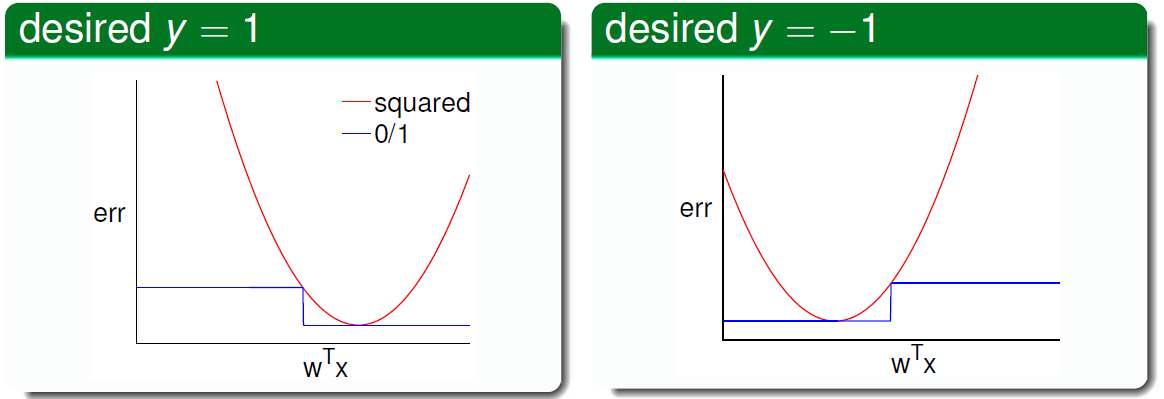
可见\(\operatorname { err } _ { 0 / 1 } < \operatorname { err } _ { \text{sqr} }\),所以可以得出:
\[\begin{aligned}
\text{classification } E_{out}(\mathbf{w})
& \leq \text{classification } E_{in}(\mathbf{w}) + \sqrt{\cdots \cdots} \\
& \leq \text{regression } E_{in}(\mathbf{w}) + \sqrt{\cdots \cdots}
\end{aligned}
\]
所以说如果回归误差作为上限很小,那么分类误差也会很小。所以线性回归可以用于分类。
由于存在误差所以可以将\(\mathbf{w}_{LIN}\)作为 PLA/Pocket 算法的初始(基础)向量。







