逻辑回归（Logistic Regression）
软性二分类（Soft Binary Classification）
逻辑回归实际上是一种软性二分类（Soft Binary Classification），与 硬性二分类（Hard Binary Classification）的区别是数据一致，但是目标函数不同，软性二分类的目标是给出分类结果为正负样本的概率分别为多少，比如预测是否发放信用卡时，不在是 0/1 ，而是预测发放信用卡的概率的是多大。
目标函数公式如下：
\[f ( \mathbf { x } ) = P ( + 1 | \mathbf { x } ) \in [ 0,1 ]
\]
逻辑假设函数（Logistic Hypothesis）
与硬二分类（perceptron）不同的是不在使用 sign 函数，取而代之的是逻辑函数 \(\theta(s)\)，利用分数（\(\mathbf{w}^{T}\mathbf{x}\)）来估计概率，所以逻辑假设函数（Logistic hypothesis）如下：
\[h(\mathbf{x})=\operatorname{\theta}\left(\mathbf{w}^{T}\mathbf{x}\right)
\]
其中 \(\theta(s)\) 的数学表达为：
\[\theta ( s ) = \frac { e ^ { s } } { 1 + e ^ { s } } = \frac { 1 } { 1 + e ^ { - s } }
\]
可以推导出 \(1 - \theta ( s ) = \theta ( -s )\)。
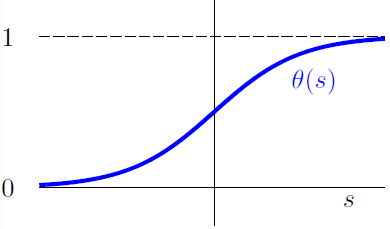
绘制出曲线如下：
可见 \(\theta(s)\) 是光滑（smooth），单调（monotonic），像 S 一样的乙状（sigmoid）函数。
逻辑假设函数的最终形式为：
\[h ( \mathbf { x } ) = \frac { 1 } { 1 + \exp \left( - \mathbf { w } ^ { T } \mathbf { x } \right) }
\]
那么其也具备 \(\theta(s)\) 的性质，即 \(1 - h ( \mathbf { x } ) = h ( \mathbf { -x } )\)。
由前所述，逻辑回归的目标函数可以获取该样本为分别为正负样本的概率：
\[P ( y | \mathbf { x } ) = \left\{ \begin{array} { l l } f ( \mathbf { x } ) & \text { for } y = + 1 \\ 1 - f ( \mathbf { x } ) & \text { for } y = - 1 \end{array} \right.
\]
交叉熵误差（Cross-Entropy Error）
现在有了逻辑假设函数，那么 \(E _ { \text {in } }(\mathbf{w})\) 如何设计呢，这里选择全部样本分类正确的概率，这里叫做 \(\text{likelihood}(h)\)：
Consider \(\mathcal { D } = \left\{ \left( \mathbf { x } _ { 1 } , 1 \right) , \left( \mathbf { x } _ { 2 } , -1 \right) , \ldots , \left( \mathbf { x } _ { N } , -1 \right) \right\}\) :
\[\begin{aligned}\text { likelihood}( h ) & = P \left( \mathrm { x } _ { 1 } \right) P( 1 | \mathrm { x }_{1}) \times P \left( \mathrm { x } _ { 2 } \right) P( -1 | \mathrm { x }_{2}) \times \ldots P \left( \mathrm { x } _ { N } \right) P( -1 | \mathrm { x }_{N}) \\& = P \left( \mathrm { x } _ { 1 } \right) h \left( \mathrm { x } _ { 1 } \right) \times P \left( \mathrm { x } _ { 2 } \right) \left( 1 - h \left( \mathrm { x } _ { 2 } \right) \right) \times \ldots P \left( \mathrm { x } _ { N } \right) \left( 1 - h \left( \mathrm { x } _ { N } \right) \right) \\
& = P \left( \mathrm { x } _ { 1 } \right) h \left( \mathrm { x } _ { 1 } \right) \times P \left( \mathrm { x } _ { 2 } \right) h \left( -\mathrm { x } _ { 2 } \right) \times \ldots P \left( \mathrm { x } _ { N } \right) h \left(- \mathrm { x } _ { N } \right) \\& = P \left( \mathrm { x } _ { 1 } \right) h \left( y_{1} \mathrm { x } _ { 1 } \right) \times P \left( \mathrm { x } _ { 2 } \right) h \left( y_{2} \mathrm { x } _ { 2 } \right) \times \ldots P \left( \mathrm { x } _ { N } \right) h \left(y_{n} \mathrm { x } _ { N } \right) \\& = \prod _ { n = 1 } ^ { N } h \left( y _ { n } \mathbf { x } _ { n } \right) \\
\end{aligned}
\]
那么最佳假设函数 \(g\) 为：
\[g = \underset { h } { \operatorname { argmax } } \operatorname { likelihood } ( h )
\]
为了方便计算这里将\(\text { likelihood} ( h )\) 做一下转换：
\[\text { likelihood} ( \mathbf{w} ) \propto \prod _ { n = 1 } ^ { N } \theta \left( y _ { n } \mathbf { w } ^ { T } \mathbf { x } _ { n } \right)
\]
现在可以将其转换为相同任务的另一种形式，将连乘和求最大值转换为累加和求最小值：
\[\begin{aligned}
\max_{\mathbf{w}} \text { likelihood} ( \mathbf{w} )
& \Rightarrow \max_{\mathbf{w}} \ln \text { likelihood} ( \mathbf{w} ) \\
& \Rightarrow \max_{\mathbf{w}} \sum_{n=1}^{N} \ln \theta \left( y _ { n } \mathbf { w } ^ { T } \mathbf { x } _ { n } \right)\\
& \Rightarrow \min_{\mathbf{w}} \frac{1}{N}\sum_{n=1}^{N} -\ln \theta \left( y _ { n } \mathbf { w } ^ { T } \mathbf { x } _ { n } \right) \\
& \Rightarrow \min_{\mathbf{w}} \frac{1}{N}\sum_{n=1}^{N} -\ln \left( \frac{1}{1 + \exp \left( y _ { n } \mathbf { w } ^ { T } \mathbf { x } _ { n } \right) }\right)\\
& \Rightarrow \min_{\mathbf{w}} \frac{1}{N}\sum_{n=1}^{N} \ln \left( 1 + \exp \left( y _ { n } \mathbf { w } ^ { T } \mathbf { x } _ { n } \right) \right)\\
& \Rightarrow \min_{\mathbf{w}} \frac{1}{N}\sum_{n=1}^{N} \text{err} \left( \mathbf { w } , \mathbf { x } _ { n } , y _ { n }\right) \Rightarrow E_{\text{in}}(\mathbf{w})
\end{aligned}
\]
其中 \(\text{err} \left( \mathbf { w } , \mathbf { x } _ { n } , y _ { n }\right) = \ln \left( 1 + \exp \left( y _ { n } \mathbf { w } ^ { T } \mathbf { x } _ { n } \right) \right)\) 被称作交叉熵误差（cross-entropy error）。
梯度下降 （Gradient Descent）
求得的\(E_{\text{in}}\) 仍然是连续的（continuous）， 可微的（differentiable），二次可微的（twice-differentiable），凸的（convex）函数。那么根据连续可微凸函数的最优必要条件梯度为零，便可以获得最优的hypothesis。
下面来推导一下梯度 \(\nabla E_{\text{in}} (\mathbf{w})\)：
为了书写方便用圆圈和方块表示两个部分：
\[E _ { \mathrm { in } } ( \mathbf { w } ) = \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \ln ( \underbrace { 1 + \exp ( \overbrace { - y _ { n } \mathbf { w } ^ { T } \mathbf { x } _ { n } }^{\bigcirc} ) } _ { \square } )
\]
那么 \(E_{\text{in}}\) 在 \(\mathbf{w}_i\) 上的偏导为：
\[\begin{aligned}
\frac { \partial E _ { \text {in } } ( \mathbf { w } ) } { \partial \mathbf { w } _ { i } }
& = \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \left( \frac { \partial \ln ( \square ) } { \partial \square } \right) \left( \frac { \partial ( 1 + \exp ( \bigcirc ) ) } { \partial \bigcirc } \right) \left( \frac { \partial - y _ { n } \mathbf { W } ^ { T } \mathbf { x } _ { n } } { \partial w _ { i } } \right)\\
& = \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \left( \frac { 1 } { \square } \right) \left( { \exp ( \bigcirc ) } \right) \left( { - y _ { n } \mathbf { x } _ { n,i } } \right)\\
& = \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \left( \frac { \exp ( \bigcirc ) } { \exp ( \bigcirc ) + 1 } \right) \left( { - y _ { n } \mathbf { x } _ { n,i } } \right)\\
& = \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \theta(\bigcirc) \left( { - y _ { n } \mathbf { x } _ { n,i } } \right)\\
\end{aligned}
\]
那么进一步可求得：
\[\nabla E_{\text{in}} (\mathbf{w}) = \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \theta(- y _ { n } \mathbf{w}^{T} \mathbf { x } _ { n }) \left( { - y _ { n } \mathbf { x } _ { n } } \right)\\
\]
如何使得梯度为零呢？
这里借鉴与PLA，使用迭代优化策略（iterative optimization approach）：
For \(t=0,1, \ldots\)
\[\mathbf { w } _ { t + 1 } \leftarrow \mathbf { w } _ { t } + \eta \mathbf { v }
\]
when stop, return last \(\mathbf{w}\) as \(g\).
其中 \(\mathbf{v}\) 为单位方向向量，即 \(||\mathbf{v}|| = 1\)；而 \(\eta\) 代表了步长，所以用为正实数。
那么优化目标便变成：
\[\min _ { \| \mathbf { v } \| = 1 } E _ { \mathrm { in } } \left( \mathbf { w } _ { t } + \eta \mathbf { v } \right)
\]
方向向量 \(\mathbf{v}\)
那么先不考虑步长，认为其非常小，那么可以通过一阶泰勒展开转换为：
\[E _ { \mathrm { in } } \left( \mathbf { w } _ { t } + \eta \mathbf { v } \right) \approx E _ { \mathrm { in } } \left( \mathbf { w } _ { t } \right) + \eta \mathbf { v } ^ { T } \nabla E _ { \mathrm { in } } \left( \mathbf { w } _ { t } \right)
\]
可以看出：
\[\min _ { \| \mathbf { v } \| = 1 } \underbrace { E _ { \text {in } } \left( \mathbf { w } _ { t } \right) } _ { \text {known } } + \underbrace { \eta } _ { \text {given positive } } \mathbf { v } ^ { T } \underbrace { \nabla E _ { \text {in } } \left( \mathbf { w } _ { t } \right) } _ { \text {known } }
\]
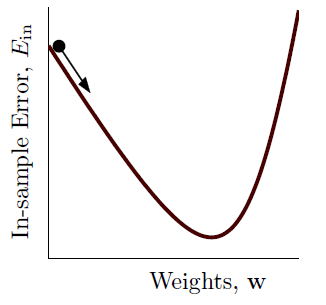
看下图，当在原始点向最优点搜索时，应当顺着负梯度方向搜索。
同时从理论上讲，在不考虑步长时，当两个向量方向相反时，其乘积最小，所以方向向量应该是与梯度方向完全相反的单位向量：
\[\mathbf { v } = - \frac { \nabla E _ { \mathrm { in } } \left( \mathbf { W } _ { t } \right) } { \left\| \nabla E _ { \mathrm { in } } \left( \mathbf { W } _ { t } \right) \right\| }
\]
那么迭代函数（\(\eta\) is small）则为：
\[\mathbf { w } _ { t + 1 } \leftarrow \mathbf { w } _ { t } - \eta \frac { \nabla E _ { \mathrm { in } } \left( \mathbf { w } _ { t } \right) } { \left\| \nabla E _ { \mathrm { in } } \left( \mathbf { w } _ { t } \right) \right\| }
\]
步长 \(\eta\)
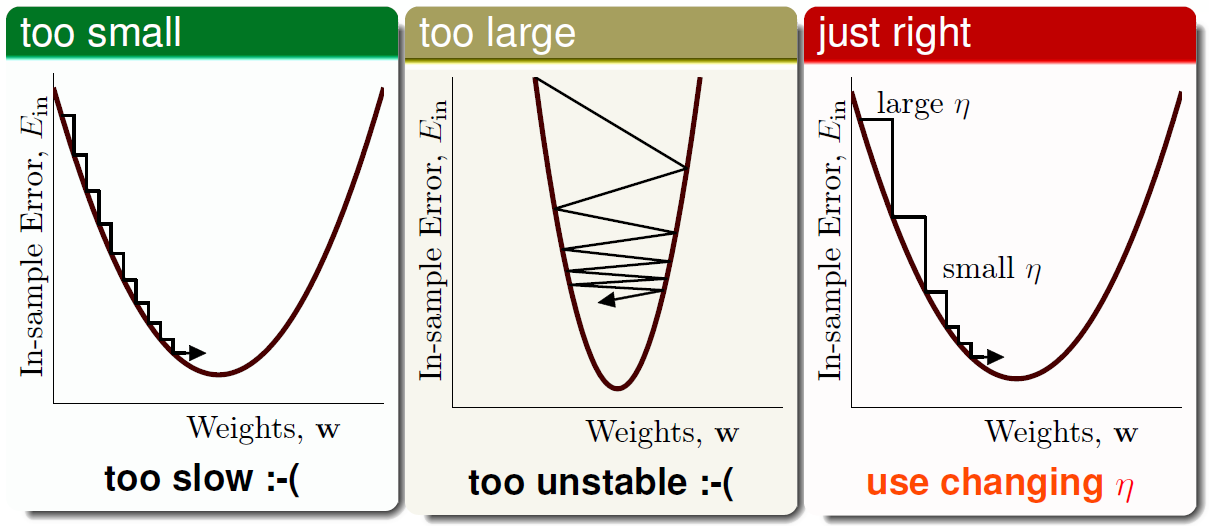
观察下面三条曲线：
可以看出步长应当随着梯度大小进行调整，也就是第三条曲线上的搜索过程是最佳的。即步长 \(\eta\) 应与 \(\left\| \nabla E _ { \mathrm { in } } \left( \mathbf { W } _ { t } \right) \right\|\) 单调（monotonic）相关。
现在令 \(\eta = \eta \cdot \left\| \nabla E _ { \mathrm { in } } \left( \mathbf { W } _ { t } \right) \right\|\) ，那么迭代式可进一步转换为：
\[\mathbf { w } _ { t + 1 } \leftarrow \mathbf { w } _ { t } - \eta { \nabla E _ { \mathrm { in } } \left( \mathbf { w } _ { t } \right) }
\]
这就是梯度下降法，一个简单而有常用的优化工具（a simple & popular optimization tool）。
算法实现
initialize \(\mathbf{w}_{0}\)
For \(t=0,1, \ldots\)
\[\nabla E_{\text{in}} (\mathbf{w}) = \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \theta(- y _ { n } \mathbf{w}^{T} \mathbf { x } _ { n }) \left( { - y _ { n } \mathbf { x } _ { n } } \right)\\
\]
\[\mathbf { w } _ { t + 1 } \leftarrow \mathbf { w } _ { t } - \eta { \nabla E _ { \mathrm { in } } \left( \mathbf { w } _ { t } \right) }
\]
- … until \(\nabla E_{\text{in}} (\mathbf{w}) = 0\) or enough iterations
return \({\mathbf{w}}_{t+1}\) as g
逻辑回归（Logistic Regression）\(\rightarrow\)分类（Classification）
在学习线性回归时就讨论过是否可以用于分类，现在进行相同的分析：
先令 \(s = \mathbf { w } ^ { T } \mathbf { x }\) ，同时当用于二分类时 \(y \in \{ - 1 , + 1 \}\) 所以各误差函数可以转换如下：
\[\begin{aligned}
\text{err}_ { \text{0/1 } } ( s , y ) & = [ \operatorname { sign } ( s ) \neq y ] = [ \operatorname { sign } ( y s ) \neq 1 ] \\
\text{err}_ { \text{SQR} } ( s , y ) & = ( y - s ) ^ { 2 } = ( y s - 1 ) ^ { 2 }\\
\text{err}_ { \text{CE } } ( s , y ) & = \ln ( 1 + \exp ( - y s ) ) \\
\text{err}_ { \text{SCE} } ( s , y ) & = \log _ { 2 } ( 1 + \exp ( - y s ) ) \end{aligned}
\]
其中 \(\text{err}_ { \text{SCE} }\) 是通过 \(\text{err}_ { \text{CE} }\) 乘以 \(1/ \ln (2)\) 获得的。
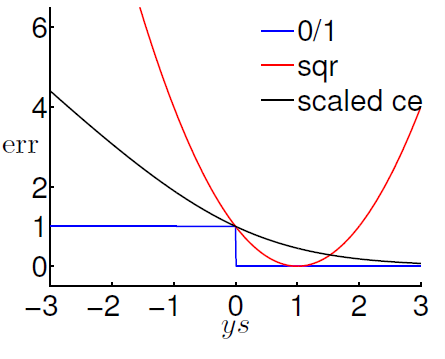
绘制出误差函数的曲线图关系（其中 \(\text{err}_ { \text{CE} }\) 与 \(\text{err}_ { \text{SCE} }\) 相似不再绘制）：
由图可知：
\[\operatorname { err } _ { 0 / 1 } ( s , y ) \leq \operatorname { err } _ { \mathrm { SCE } } ( s , y ) = \frac { 1 } { \ln 2 } \operatorname { err } _ { \mathrm { CE } } ( s , y )
\]
进而推导得：
\[E _ { \mathrm { in } } ^ { 0 / 1 } ( \mathbf { w } ) \leq E _ { \mathrm { in } } ^ { \mathrm { SCE } } ( \mathrm { W } ) = \frac { 1 } { \ln 2 } E _ { \mathrm { in } } ^ { \mathrm { CE } } ( \mathbf { w } )\\
E _ { \mathrm { out } } ^ { 0 / 1 } ( \mathbf { w } ) \leq E _ { \mathrm { out } } ^ { \mathrm { SCE } } ( \mathrm { W } ) = \frac { 1 } { \ln 2 } E _ { \mathrm { out } } ^ { \mathrm { CE } } ( \mathbf { w } )
\]
那么可以得知：
\[\begin{aligned}
E _ { \mathrm { out } } ^ { 0 / 1 } ( \mathbf { w } ) & \leq E _ { \mathrm { in } } ^ { 0 / 1 } ( \mathbf { w } ) + \Omega ^ { 0 / 1 } \\
& \leq \frac{1}{\ln 2} E _ { \mathrm { in } } ^ { CE } ( \mathbf { w } ) + \Omega ^ { 0 / 1 }
\end{aligned}
\]
或者：
\[\begin{aligned} E _ { \text {out } } ^ { 0 / 1 } ( \mathbf { w } ) & \leq \frac { 1 } { \ln 2 } E _ { \text {out } } ^ { \mathrm { CE } } ( \mathbf { W } ) \\ & \leq \frac { 1 } { \ln 2 } E _ { \text {in } } ^ { \mathrm { CE } } ( \mathbf { W } ) + \frac { 1 } { \ln 2 } \Omega ^ { \mathrm { CE } } \end{aligned}
\]
进而得知：
\[\text { small } E _ { \mathrm { in } } ^ { \mathrm { CE } } ( \mathbf { w } ) \Rightarrow \text { small } E _ { \mathrm { out } } ^ { 0 / 1 } ( \mathbf { w } )
\]
所以逻辑回归可以用于分类。
实际运用中：
- linear regression sometimes used to set w0 for PLA/pocket/logistic regression
线性回归可用于获取PLA/pocket/logistic regression的初始权重向量
- logistic regression often preferred over pocket
逻辑回归比口袋算法更为常用
随机梯度下降 （Stochastic Gradient Descent）
随机梯度下降的思想为：
\[\text{stochastic gradient} = \text{true gradient} + \text{zero-mean ‘noise’ directions}
\]
即认为在迭代足够多步后：
\[\text{average true gradient} \approx \text{average stochastic gradient}
\]
其迭代公式为：
\[\mathbf { w } _ { t + 1 } \leftarrow \mathbf { w } _ { t } + \eta \underbrace { \theta \left( - y _ { n } \mathbf { w } _ { t } ^ { T } \mathbf { x } _ { n } \right) \left( y _ { n } \mathbf { x } _ { n } \right) } _ { - \nabla \operatorname { err } \left( \mathbf { w } _ { t } , \mathbf { x } _ { n } , y _ { n } \right) }
\]
由此看出其使用单个样本的误差梯度替换全部的梯度，将时间复杂度由 \(O(N)\) 降为 \(O(1)\) 。
