机器学习中特征转换或利用是整个流程中的核心内容,这里介绍三个与之有关的三个主流技术:
- Embedding Numerous Features: how to exploit and regularize
numerous features? \(\rightarrow\) inspires Support Vector Machine (SVM) model (如何挖掘利用众多特征和控制复杂度)
- Combining Predictive Features: how to construct and blend
predictive features? \(\rightarrow\) Inspires Adaptive Boosting (AdaBoost) model (如何构造并混合一些预测特征)
- Distilling Implicit Features: how to identify and learn implicit
features? \(\rightarrow\) inspires Deep Learning model (如何学出或找出一些特征)
线性支持向量机 (Linear Support Vector Meachine)
基本概念
实际上相当于“大间隔的分割超平面 ” (Large - Margin Separating Hyperplane)。什么意思呢?
以线性分类模型 PLA 为例,其最终目标是找出一个超平面将所有的样本分割开。支持向量机实际上是在此基础上,保证离分割线最近的一些样本(\(\mathbf{x}_{n}\))与超平面之间的距离(distance to closest \(\mathbf{x}_{n}\))尽量大。这使得对噪声的容忍度(amount of noise tolerance)更大,或者说该超平面鲁棒性(robustness of hyperplane)更强。(more robust because of larger distance to closest \(\mathbf{x}_{n}\))。
这样可以假设边界不是一条宽度不计的超平面,而是一个有宽度的胖超平面(fat hyperplane)。那么这里的胖度实际上就相当于鲁棒性即 \(\text{robustness} \equiv \text{fatness}\)。
那么现在的目标就是找出那个最胖的一个超平面(fattest separating hyperplane)。
\[\begin{aligned}
\max _{\mathbf{w}} \quad & \text {fatness }(\mathbf{w})\\
\text{subject to} \quad &\mathrm{w} \text{ classifies every } \left(\mathrm{x}_{n}, y_{n}\right) \text{ correctly}\\
& \text {fatness }(\mathbf{w})=\min _{n=1, \ldots, N} \operatorname{distance}\left(\mathbf{x}_{n}, \mathbf{w}\right)
\end{aligned}
\]
至此胖胖的超平面正式叫做间隔(margin),据此将上式改写为:
\[\begin{aligned}
\max _{\mathbf{w}} \quad & \text {margin }(\mathbf{w})\\
\text{subject to} \quad & y_{n} \mathbf{w}^{T}\mathbf{x} > 0\\
& \text {margin }(\mathbf{w})=\min _{n=1, \ldots, N} \operatorname{distance}\left(\mathbf{x}_{n}, \mathbf{w}\right)
\end{aligned}
\]
因为间隔的求取需要将 \(\mathbf{w}_0\) 和 \((\mathbf{w}_0, \cdots , \mathbf{w}_d)\) 分开 (to be derived),所以在本章中假设函数(超平面)的表达式为:
\[h(\mathbf{x})=\operatorname{sign}\left(\mathbf{w}^{T}\mathbf{x} + b\right)
\]
最优化问题转换
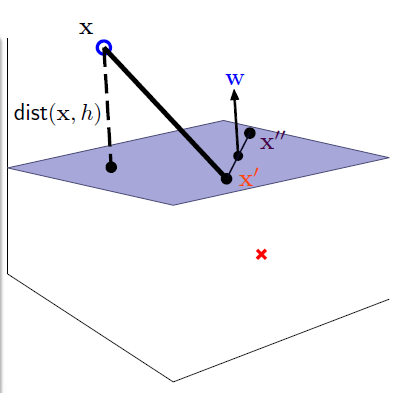
第一步:获取距离(distance)
![在这里插入图片描述]()
假设超平面上的任意两点 \(\mathbf{x}^{\prime}\) 和 \(\mathbf{x}^{\prime \prime}\),那么:
- \(\mathbf{w}^{T}\mathbf{x}^{\prime} = -b\),\(\mathbf{w}^{T}\mathbf{x}^{\prime \prime} = -b\)
- \(\mathbf{w} \perp \text{ hyperplane}\):
\[\left(\begin{array}{cc}
\mathbf{w}^{T} & \underbrace{\left(\mathbf{x}^{\prime \prime}-\mathbf{x}^{\prime}\right)}_\text { vector on hyperplane }
\end{array}\right)=0
\]
- 所以样本到超平面(hyperplane)距离的计算公式为 \(\text{distance }= \text{project }(\mathbf{x} - \mathbf{x}^{\prime}) \text{ to } \perp \text{ hyperplane}\)。
即:
\[\operatorname{distance}(\mathbf{x}, b, \mathbf{w})=\left|\frac{\mathbf{w}^{T}}{\|\mathbf{w}\|}\left(\mathbf{x}-\mathbf{x}^{\prime}\right)\right| \stackrel{(1)}{=} \frac{1}{\|\mathbf{w}\|}\left|\mathbf{w}^{T} \mathbf{x}+b\right|
\]
第二步:去绝对值号
对于分割超平面(separating hyperplane)有:
\[y_{n}\left(\mathbf{w}^{T} \mathbf{x}_{n}+b\right)>0
\]
距离公式可以进一步写为:
\[\operatorname{distance}(\mathbf{x}, b, \mathbf{w})= \frac{1}{\|\mathbf{w}\|}\left|\mathbf{w}^{T} \mathbf{x}+b\right|= \frac{1}{\|\mathbf{w}\|} y_{n} \left(\mathbf{w}^{T} \mathbf{x}+b\right)
\]
第三步:缩放 margin
将最小的 margin 缩放至 \(\frac{1}{\|\mathbf{w}\|}\),即令:
\[\min_{n=1,\cdots,N} y_{n} \left(\mathbf{w}^{T} \mathbf{x}+b\right) = 1
\]
可以看出此缩放跟样本无关,只是将 \(\mathbf{x}\) 和 \(b\) 进行了缩放。至此可以将约束条件转换为其必要条件:
\[y_{n}\left(\mathbf{w}^{T} \mathbf{x}_{n}+b\right) \geq 1 \text{ for all } n
\]
第四步:去根号,将最小化改为最大化
由于根号不好求取,所以这里将其转换为等价最优化问题求其倒数平方的最小值,并添加 \(\frac{1}{2}\)。
\[\begin{aligned}
\min _{b, w} \quad & \frac{1}{2} w^{T} w \\
\text{subject to }\quad & y_{n}\left(\mathbf{w}^{T} \mathbf{x}_{n}+b\right) \geq 1 \text{ for all } n
\end{aligned}
\]
第五步:转换为二次规划问题
二次规划(QP,全称 quadratic programming),是一个较为容易的优化问题。二次规划的标准形式为:
\[\begin{aligned}
\text{optimal } \mathrm{u} \leftarrow & \mathrm{QP}(\mathrm{Q}, \mathrm{p}, \mathrm{A}, \mathrm{c}) \\
\min _{u} \quad & \frac{1}{2} u^{T} Q u+p^{T} u\\
\text{subject to }\quad & \mathbf{a}_{m}^{T} \mathbf{u} \geq c_{m}
\text{ for } m=1,2, \ldots, M
\end{aligned}
\]
对比支持向量机的最优化问题的数学表达,可以得出:
\[\begin{aligned}
\text{objective function:} \quad &\mathbf{u}=\left[\begin{array}{l}
b \\
\mathbf{w}
\end{array}\right] ; Q=\left[\begin{array}{ll}
0 & \mathbf{0}_{d}^{T} \\
\mathbf{0}_{d} & \mathrm{I}_{d}
\end{array}\right] ; \mathbf{p}=0_{d+1}\\
\text{constraints:} \quad &\mathbf{a}_{n}^{T}=y_{n}\left[\begin{array}{ll}
1 & \mathbf{x}_{n}^{T}
\end{array}\right] ; c_{n}=1 ; M=N
\end{aligned}
\]
线性 SVM(with QP Solver)的训练步骤
- \(\mathbf{u}=\left[\begin{array}{l} b \mathbf{w} \end{array}\right] ; Q=\left[\begin{array}{ll}
0 & \mathbf{0}_{d}^{T} \\
\mathbf{0}_{d} & \mathrm{I}_{d}
\end{array}\right] ; \mathbf{p}=0_{d+1}
\mathbf{a}_{n}^{T}=y_{n}\left[\begin{array}{ll}
1 & \mathbf{x}_{n}^{T}
\end{array}\right] ; c_{n}=1 ; M=N\)
- \(\left[\begin{array}{l}b \\ w\end{array}\right] \leftarrow Q P(Q, p, A, c)\)
- return \(b\,\& \,w\) as \(g_{\mathbf{svm}}\)
以二维平面为例求取支持向量机:
假设样本的分布为:
\[X=\left[\begin{array}{ll}
0 & 0 \\
2 & 2 \\
2 & 0 \\
3 & 0
\end{array}\right] \quad y=\left[\begin{array}{l}
-1 \\
-1 \\
+1 \\
+1
\end{array}\right] \quad \begin{aligned}
&-b \geq 1 &(i)\\
-2 w_{1}-2 w_{2}& - b \geq 1&(ii) \\
2 w_{1} \quad \quad \quad &+b \geq 1 &(iii)\\
3 w_{1} \quad \quad \quad &+b \geq 1 &(iv)
\end{aligned}
\]
可以求解的:
\[g_{\mathrm{svm}}(\mathbf{x})=\operatorname{sign}\left(x_{1}-x_{2}-1\right)
\]
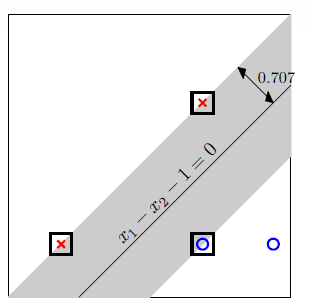
示意图如下:
![在这里插入图片描述]()
其中画方框的边缘样本(boundary example) 叫做支持向量(support vector),而支持向量机则是通过这些支持向量求取最胖的超平面,这便是支持向量机的来源。
大间隔(Large-Margin)的意义
与L2正则化的关系
写到这里肯定会想到,采用最大间隔的超平面的意义是什么?
现在将其与 L2范数正则化(weight-decay regularization)进行对比:
\[\begin{array}{c|c|c}
& \text { minimize } & \text { constraint } \\
\hline \text { regularization } & E_{\text {in }} & \mathbf{w}^{T} \mathbf{w} \leq C \\
\hline \text { SVM } & \mathbf{w}^{T} \mathbf{w} & E_{\text {in }}=0 \text { [and more] }
\end{array}
\]
可见实际上线性支持向量机(Linear SVM)是一种以 \(E_{\text {in }}=0\) 为条件的L2范数正则化。
大间隔算法(large-margin algorithm)
SVM 可以理解为一种大间隔算法(large-margin algorithm)\(\mathcal{A}_{\rho}\):returns \(g\) with \(\operatorname{margin}(g) \geq \rho\) (if exists), or 0 otherwise。
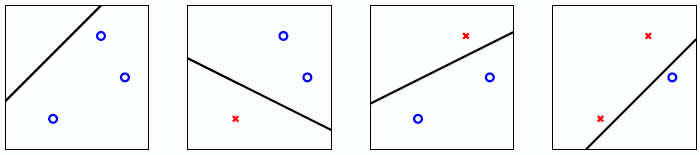
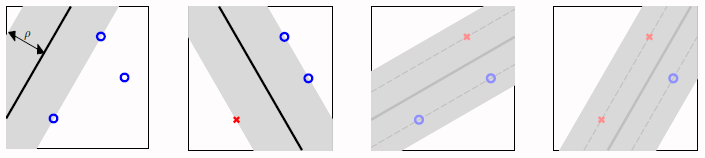
当间隔不断扩大时,有些可以 shatter 的情况会因为在间隔内而不能 shatter。
当 \(\rho = 0\) 时,输入个数为三时,可以shatter。
![在这里插入图片描述]()
当 \(\rho = 1.126\) 时,输入个数为三时,不可以shatter了。
![在这里插入图片描述]()
这代表了更少的二分法(fewer dichotomies)\(\Rightarrow\) 更小的 ‘VC dim’ \(\Rightarrow\) 更好的泛化能力。
核支持向量机(Kernel SVM)
大间隔超平面(Large-Margin Hyperplane)
下面列举以下原来所求取的模型的特点与大间隔超平面算法做对比:
\[\begin{array}{c|c|c|c}
& \begin{array}{c}
\text { large-margin } \\
\text { hyperplanes }
\end{array} & \text { hyperplanes } & \begin{array}{c}
\text { hyperplanes } \\
+\text { feature transform } \Phi
\end{array} \\
\hline \# & \text { even fewer } & \text { not many } & \text { many } \\
\hline \text { boundary } & \text { simple } & \text { simple } & \text { sophisticated }
\end{array}
\]
其中 \(\#\) 代表了 \(\mathcal{H}\) 的大小。可以观察图表看出,大间隔超平面可以保证更小的 \(\mathcal{H}\) ,虽然边界简单。所以说非线性支持向量机可能可以实现:
\[\begin{array}{c|c}
& \text { large-margin } \\
& \text { hyperplanes } \\
& +\text { numerous feature transform } \Phi \\
\hline
\# & \text { not many } \\
\hline
\text { boundary } & \text { sophisticated }
\end{array}
\]
即边界复杂度上升,但 \(\mathcal{H}\) 的大小仍然不算太大。
非线性支持向量机(Non-Linear SVM)
经过非线性转换后最优化问题变为:
\[\begin{array}{ll}
\min _{b, w} & \frac{1}{2} \mathbf{w}^{T} \mathbf{w} \\
\text { s.t. } & y_{n}(\mathbf{w}^{T} \underbrace{\mathbf{z}_{n}}_{\Phi\left(\mathbf{x}_{n}\right)}+b) \geq 1 \\
& \text { for } n=1,2, \ldots, N
\end{array}
\]
实现步骤转换为:
- \(\begin{aligned}
\mathbf{u}=\left[\begin{array}{l}
b \\
\mathbf{w}
\end{array}\right] ; Q=\left[\begin{array}{ll}
0 & \mathbf{0}_{\tilde{d}}^{T} \\
\mathbf{0}_{\tilde{d}} & \mathrm{I}_{\tilde{d}}
\end{array}\right] ; \mathbf{p}=0_{\tilde{d}+1} \mathbf{a}_{n}^{T}=y_{n}\left[\begin{array}{ll}
1 & \mathbf{z}_{n}^{T}
\end{array}\right] ; c_{n}=1 ; M=N
\end{aligned}\)
- \(\left[\begin{array}{l}b \\ w\end{array}\right] \leftarrow Q P(Q, p, A, c)\)
- \(\text { return } b \in \mathbb{R} \, \& \, \mathrm{w} \in \mathbb{R}^{d} \text { with }g_{\mathrm{svm}}(\mathbf{x})=\operatorname{sign}\left(\mathbf{w}^{T} \mathbf{\Phi}(\mathbf{x})+b\right)\)
但是可以明显看出随着 \(\mathbf{\Phi}(\mathbf{x})\) 非线性转换函数维度 \({\tilde{d}}\) 的增加,计算的复杂度也随之增加,那么如何解决该问题呢,下面进行解决 —— 核技术。
对偶支持向量机(Dual SVM)
在使用核技术之前需要先将支持向量机转换为对偶问题。
对偶问题(Dual Problem)
首先将其转换为无约束最优化问题:写出其拉格朗日方程(Lagrange Function),其中 \(\alpha_{n}\) 为拉格朗日乘数(Lagrange Multiplier)
\[\mathcal{L}(b, \mathbf{w}, \alpha)=
\underbrace{\frac{1}{2} \mathbf{w}^{T} \mathbf{w}}_{\text {objective }}+\sum_{n=1}^{N} \alpha_{n}(\underbrace{1-y_{n}\left(\mathbf{w}^{T} \mathbf{z}_{n}+b\right)}_{\text {constraint }})
\]
那么 SVM 的等价问题可写为:
\[\mathrm{SVM} \equiv \min_{b, \mathrm{w}}\left(\max _{\text{all } \alpha_{n} \geq 0} \mathcal{L}(b, \mathbf{w}, \alpha)\right)
\]
其中对于 \((b, \mathbf{w})\) 存在任何违背约束条件时:
\[\max _{\text {all } \alpha_{n} \geq 0}\left(\square+\sum_{n} \alpha_{n}(\text { some positive })\right) \rightarrow \infty
\]
这是因为求取最大值的操作,在 constraint 部分为 positive 时,\(\alpha_{n}\) 会无限增长,最终导致趋近于正无穷。
其中对于 \((b, \mathbf{w})\) 均符合约束条件时:
\[\max _{\text {all } \alpha_{n} \geq 0}\left(\square+\sum_{n} \alpha_{n}(\text { all non-positive })\right)=\square
\]
这是因为求取最大值的操作,在 constraint 部分为 negative 时,\(\alpha_{n}\) 会无限趋近于零,最终导致后半部分趋近于零。
那么 SVM 的等价问题可进一步写为:
\[\mathrm{SVM} = \min _{b, \mathrm{w}}\left(\infty \text { if violate } ; \frac{1}{2} \mathrm{w}^{T} \mathrm{w} \text { if feasible }\right)
\]
对于任何一个 \(\alpha_{n}^{\prime} \geq 0\) 的 \(\alpha^{\prime}\)有以下不等式:
\[\min _{b, \mathbf{w}}\left(\max _{\text {all } \alpha_{n} \geq 0} \mathcal{L}(b, \mathbf{w}, \boldsymbol{\alpha})\right) \geq \min _{b, \mathbf{w}} \mathcal{L}\left(b, \mathbf{w}, \alpha^{\prime}\right)
\]
因为最大值 \(\geq\) 任何值(包括最佳值),即。
\[\underbrace{\min _{b, w}\left(\max _{\text {all } \alpha_{n} \geq 0} \mathcal{L}(b, \mathbf{w}, \alpha)\right)}_{\text{equiv. to original (primal) SVM}} \geq \underbrace{\max _{\text {all } \alpha_{n} \geq 0} \left( \min _{b, w} \mathcal{L}\left(b, \mathbf{w}, \alpha^{\prime}\right)\right)}_{\text {Lagrange dual problem }}
\]
在上述公式中:
如果是 \(\leq\) :代表了弱对偶;
如果是 \(=\) :代表了强对偶;对于QP(二次规划问题)需要满足以下条件:
- 原问题的凸的
- 原问题是可行的(是 \(\Phi\) 可分的)
- 线性约束
拉格朗日的对偶问题:实际上就是求原问题下界的最大值。
所以说线性支持向量机是存在对偶最优解的。
拉格朗日对偶问题(Lagrange Dual Problem)
对偶问题的显式为:
\[\max _{\text {all } \alpha_{n} \geq 0}\left(\min _{b, w} \underbrace{\frac{1}{2} \mathbf{w}^{T} \mathbf{w}+\sum_{n=1}^{N} \alpha_{n}\left(1-y_{n}\left(\mathbf{w}^{T} \mathbf{z}_{n}+b\right)\right)}_{\mathcal{L}(b, \mathbf{w}, \alpha)}\right)
\]
由于里面优化问题为无约束最优化问题,所以其最优解满足:
\[\frac{\partial \mathcal{L}(b, \mathbf{w}, \alpha)}{\partial b}=0=-\sum_{n=1}^{N} \alpha_{n} y_{n}
\]
所以当以此为约束条件时将不影响最优解得求取,那么最优化问题可以进行以下转换:
\[\max _{\text {all } \alpha_{n} \geq 0}\left(\min _{b, w} {\frac{1}{2} \mathbf{w}^{T} \mathbf{w}+\sum_{n=1}^{N} \alpha_{n}\left(1-y_{n}\left(\mathbf{w}^{T} \mathbf{z}_{n}+b\right)\right)}\right) \\
\Rightarrow \max _{\text {all } \alpha_{n} \geq 0}\left(\min _{b, w} {\frac{1}{2} \mathbf{w}^{T} \mathbf{w}+\sum_{n=1}^{N} \alpha_{n}\left(1-y_{n}\left(\mathbf{w}^{T} \mathbf{z}_{n}\right)\right) + \sum_{n=1}^{N} \alpha_{n} y_{n} \cdot b}\right) \\
{\mathop {\Longrightarrow}\limits^{\sum_{n=1}^{N} \alpha_{n} y_{n} = 0} \max _{\text {all } \alpha_{n} \geq 0, \sum y_{n} \alpha_{n}=0}\left(\min _{b, \mathbf{w}} \frac{1}{2} \mathbf{w}^{T} \mathbf{w}+\sum_{n=1}^{N} \alpha_{n}\left(1-y_{n}\left(\mathbf{w}^{T} \mathbf{z}_{n}\right)\right)\right)}\\
\]
由于里面优化问题为无约束最优化问题,所以其最优解同时也满足:
\[\frac{\partial \mathcal{L}(b, w, \alpha)}{\partial w_{i}}=0=w_{i}-\sum_{n=1}^{N} \alpha_{n} y_{n} z_{n, i} \Rightarrow \mathbf{w}=\sum_{n=1}^{N} \alpha_{n} y_{n} \mathbf{z}_{n}
\]
所以该优化问题可以进一步转换为:
\[\begin{array}{ll}
&\max\limits_{ \text { all } \alpha_{n} \geq 0, \sum y_{n} \alpha_{n}=0, \mathbf{w}=\sum \alpha_{n} y_{n} z_{n}}\left(\min _{b, w} \frac{1}{2} \mathbf{w}^{T} \mathbf{w}+\sum_{n=1}^{N} \alpha_{n}-\mathbf{w}^{T} \mathbf{w}\right) \\
\Longleftrightarrow &\max\limits_{ \text { all } \alpha_{n} \geq 0, \sum y_{n} \alpha_{n}=0, \mathbf{w}=\sum \alpha_{n} y_{n} z_{n}}-\frac{1}{2}\left\|\sum_{n=1}^{N} \alpha_{n} y_{n} \mathbf{z}_{n}\right\|^{2}+\sum_{n=1}^{N} \alpha_{n}
\end{array}
\]
KKT 优化条件(Karush-Kuhn-Tucker Conditions)
KKT条件是对偶问题的优化的充要条件:
- 原问题的可行条件:\(y_{n}\left(\mathbf{w}^{T} \mathbf{z}_{n}+b\right) \geq 1\)
- 对偶问题的可行条件:\(\alpha_{n} \geq 0\)
- 对偶问题的内部最小化问题的最优条件:\(\sum y_{n} \alpha_{n}=0 ; \mathbf{w}=\sum \alpha_{n} y_{n} \mathbf{z}_{n}\)
- 原问题的内部最大化问题的最优条件:\(\alpha_{n}\left(1-y_{n}\left(\mathbf{w}^{T} \mathbf{z}_{n}+b\right)\right)=0\) (complementary slackness)
现在可以通过最优化 \(\alpha\) 根据KKT条件求解 \((b,\mathbf{w})\)。
求解对偶 SVM(Lagrange Dual SVM)
第一步:求解QP问题,获得\(\alpha\)
\[\begin{aligned}
\min _{\alpha} \quad & \frac{1}{2} \sum_{n=1}^{N} \sum_{m=1}^{N} \alpha_{n} \alpha_{m} y_{n} y_{m} \mathbf{z}_{n}^{T} \mathbf{z}_{m}-\sum_{n=1}^{N} \alpha_{n} \\
\text {subject to} \quad & \sum_{n=1}^{N} y_{n} \alpha_{n}=0 \\
& \alpha_{n} \geq 0, \text { for } n=1,2, \ldots, N
\end{aligned}
\]
可以看出这里有:\(N\) 个变量 \(\alpha_n\) 以及 \(N + 1\) 个线性约束条件。
转换为经典的 QP 问题
\[\begin{aligned}
\min _{\alpha} \quad & \frac{1}{2} \alpha^{T} Q \alpha+p^{T} \alpha \\
\text{subject to } \quad & \underbrace{\mathbf{a}_{i}^{T} \boldsymbol{\alpha} \geq c_{i} \quad \text{for } i=1,2, \ldots}_{A^{T} \alpha \geq C}
\end{aligned}
\]
其中
- \(q_{n, m}=y_{n} y_{m} \mathbf{z}_{n}^{T} \mathbf{z}_{m}\)
- \(\mathbf{p}=-\mathbf{1}_{N \times 1}\)
- \(\mathbf{a}_{\geq}=\mathbf{y}, \mathbf{a}_{\leq}=-\mathbf{y},\mathbf{a}_{n}^{T}=n\) - th unit direction \(\Rightarrow A = \left[a_{\geq},a_{\leq} ,a_{n} \right]\)
- \(c_{\geq}=0, c_{\leq}=0 ; c_{n}=0 \Rightarrow c=\left[c_{\geq},c_{\leq} ,c_{n} \right]\)
第二步:根据KKT,获得\((b,\mathbf{w})\)
根据KKT条件中的第三条:\(\mathbf{w}=\sum \alpha_{n} y_{n} \mathbf{z}_{n}\)
根据KKT条件中的第四条:找出\(\alpha_{n}>0\) 便可据此求得 \(b=y_{n}-\mathbf{w}^{T} \mathbf{z}_{n}\)。\(\Rightarrow\) 假设不存在 \(\alpha_{n}>0\) 即 \(\alpha_{n}=0\),那么根据KKT条件中的第三条有对于任意的 \(n\) 有 \(w_n = 0\),同时KKT条件中的第一条有 \(y_{n}b \geq 1\),只有当样本种类单一(只有一类)时:才能满足此条件,显然不成立(这只有在数据严重不平衡才会存在),所以当数据得当时,一定可以求出 \(b\)。
值得注意的是:与 PLA 通过错误点校正相仿,SVM只通过支持向量进行校正。
核技巧(kernel trick)
在前文中虽然可以看出将问题转变为 在 \(N + 1\) 个线性约束条件下,求解\(N\) 个变量 \(\alpha_n\)。但是 \(q_{n, m}=y_{n} y_{m} \mathbf{z}_{n}^{T} \mathbf{z}_{m}\),需要在 \(\tilde d\) 维空间上进行 \(\mathbf{z}_{m}\) 和 \(\mathbf{z}_{n}\) 内积的求取。如何加速这一过程呢?在映射(升维)之前将内积求出,至此引出了核技术。
以 \(\Phi_{2}\) 的快速内积为例:
\(\Phi_{2}\) 即二阶多项式转换:
\[\Phi_{2}(\mathbf{x})=\left(1, x_{1}, x_{2}, \ldots, x_{d}, x_{1}^{2}, x_{1} x_{2}, \ldots, x_{1} x_{d}, x_{2} x_{1}, x_{2}^{2}, \ldots, x_{2} x_{d}, \ldots, x_{d}^{2}\right)
\]
其内积可以转换为:
\[\begin{aligned}
\Phi_{2}(\mathrm{x})^{T} \Phi_{2}\left(\mathrm{x}^{\prime}\right) &=1+\sum_{i=1}^{d} x_{i} x_{i}^{\prime}+\sum_{i=1}^{d} \sum_{j=1}^{d} x_{i} x_{j} x_{i}^{\prime} x_{j}^{\prime} \\
&=1+\sum_{i=1}^{d} x_{i} x_{i}^{\prime}+\sum_{i=1}^{d} x_{i} x_{i}^{\prime} \sum_{j=1}^{d} x_{j} x_{j}^{\prime} \\
&=1+\mathrm{x}^{T} \mathrm{x}^{\prime}+\left(\mathrm{x}^{T} \mathrm{x}^{\prime}\right)\left(\mathrm{x}^{T} \mathrm{x}^{\prime}\right)
\end{aligned}
\]
即\(\Phi_{2}\) 的转换和内积操作时间复杂度为:\(O(d)\) 而不是原来的 \(O(d^2)\)。
至此给出定义 :Kernel = Transform + Inner Product。即 transform \(\Phi \Longleftrightarrow\) kernel function: \(K_{\Phi}\left(\mathbf{x}, \mathbf{x}^{\prime}\right) \equiv \Phi(\mathbf{x})^{T} \mathbf{\Phi}\left(\mathbf{x}^{\prime}\right)\)。
那么二阶多项式转换的核函数可写为:
\[\Phi_{2} \Longleftrightarrow K_{\Phi_{2}}\left(\mathbf{x}, \mathbf{x}^{\prime}\right)=1+\left(\mathbf{x}^{T} \mathbf{x}^{\prime}\right)+\left(\mathbf{x}^{T} \mathbf{x}^{\prime}\right)^{2}
\]
至此可以将QP问题中涉及转换后内积求解的部分全部转换:
- 二次项系数 \(q_{n, m}=y_{n} y_{m} \mathbf{z}_{n}^{T} \mathbf{z}_{m}=y_{n} y_{m} K\left(\mathbf{x}_{n}, \mathbf{x}_{m}\right)\)
- 最佳偏差系数 \(b\) from \(\mathrm{SV}\left(\mathrm{x}_{s}, y_{s}\right)\) :
\[b=y_{s}-\mathbf{w}^{T} \mathbf{z}_{s}=y_{s}-\left(\sum_{n=1}^{N} \alpha_{n} y_{n} \mathbf{z}_{n}\right)^{T} \mathbf{z}_{s}=y_{s}-\sum_{n=1}^{N} \alpha_{n} y_{n}\left(K\left(\mathbf{x}_{n}, \mathbf{x}_{s}\right)\right)
\]
- 最佳假设函数 \(g_{\text {svm }}\) for test input \(\mathbf{x}\) :
\[g_{\mathrm{svm}}(\mathrm{x})=\operatorname{sign}\left(\mathbf{w}^{T} \Phi(\mathbf{x})+b\right)=\operatorname{sign}\left(\sum_{n=1}^{N} \alpha_{n} y_{n} K\left(\mathbf{x}_{n}, \mathbf{x}\right)+b\right)
\]
所以核技巧使用有效的和函数,避免了在 \(\tilde d\) 维空间上进行计算操作。
核支持向量机的具体实现步骤为:
- \(q_{n, m}=y_{n} y_{m} K\left(\mathbf{x}_{n}, \mathbf{x}_{m}\right) ; \mathbf{p}=-\mathbf{1}_{N} ;(\mathrm{A}, \mathbf{c})\) for equ./bound constraints
- \(\alpha \leftarrow \mathrm{QP}\left(\mathrm{Q}_{\mathrm{D}}, \mathrm{p}, \mathrm{A}, \mathrm{c}\right)\)
- \(b \leftarrow\left(y_{s}-\sum\limits_{\text {SV indices } n} \alpha_{n} y_{n} K\left(\mathrm{x}_{n}, \mathrm{x}_{s}\right)\right) \text { with } \mathrm{SV}\left(\mathrm{x}_{s}, y_{s}\right)\)
- return SVs and their \(\alpha_{n}\) as well as \(b\) such that for new \(\mathbf{x}\)
\[g_{\mathrm{svm}}(\mathbf{x})=\operatorname{sign}\left(\underset{\text { SV indices } n}{\sum} \alpha_{n} y_{n} K\left(\mathbf{x}_{n}, \mathbf{x}\right)+b\right)
\]
时间复杂度分析:
- 上述第一步中每一个 \(q_{n, m}=y_{n} y_{m} K\left(\mathbf{x}_{n}, \mathbf{x}_{m}\right)\) 的时间复杂度为 kernel evaluation,同时 \(\mathrm{Q}_{\mathrm{D}}\) 中有 \(N^2\) 个元素,所以总时间复杂度为: \(O(N^2) \cdot (\text{kernel evaluation})\)
- 上述第二步中的时间复杂度为带有 \(N\) 个变量和 \(N+1\) 约束的二次规划问题的时间消耗。
- 上述第三步和第四步的时间复杂度为 \(O(\#SV) \cdot (\text{kernel evaluation})\) ,其中 \(\#SV\) 为支持向量的个数
所以实际上核支持向量机是使用计算技巧避免了依赖于映射空间维度 \(\tilde d\) 并只需使用支持向量进行预测。
多项式核函数(Polynomial Kernel)
在原来的 \(\Phi_{2}\) 基础上赋予不一样的系数,可以将其转换为一下形式:
\[\Phi_{2}(\mathbf{x})=\left(1, \sqrt{2} x_{1}, \ldots, \sqrt{2} x_{d}, x_{1}^{2}, \ldots, x_{d}^{2}\right) \\
\Leftrightarrow K_{2}\left(\mathbf{x}, \mathbf{x}^{\prime}\right)=1+2 \mathbf{x}^{T} \mathbf{x}^{\prime}+\left(\mathbf{x}^{T} \mathbf{x}^{\prime}\right)^{2}
\]
进一步泛化:
\[\Phi_{2}(\mathbf{x})=\left(1, \sqrt{2 \gamma} x_{1}, \ldots, \sqrt{2 \gamma} x_{d}, \gamma x_{1}^{2}, \ldots, \gamma x_{d}^{2}\right) \\
\Leftrightarrow K_{2}\left(\mathbf{x}, \mathbf{x}^{\prime}\right)=1+2 \gamma \mathbf{x}^{T} \mathbf{x}^{\prime}+\gamma^{2}\left(\mathbf{x}^{T} \mathbf{x}^{\prime}\right)^{2}
\]
至此可以写出二阶多项式核的一般形式:
\[K_{2}\left(\mathbf{x}, \mathbf{x}^{\prime}\right)=\left(1+\gamma \mathbf{x}^{T} \mathbf{x}^{\prime}\right)^{2} \text { with } \gamma>0
\]
虽然随着 \(\gamma\) 的变换,该核函数的power是一样的,但是其内积不同,也就是几何定义中的距离不同。
那么据此可以写出通用的多项式核(General Polynomial Kernel):
\[\begin{aligned}
K_{1}\left(\mathbf{x}, \mathbf{x}^{\prime}\right) &=\left(0+1 \cdot \mathbf{x}^{T} \mathbf{x}^{\prime}\right)^{1} \\
K_{2}\left(\mathbf{x}, \mathbf{x}^{\prime}\right) &=\left(\zeta+\gamma \mathbf{x}^{T} \mathbf{x}^{\prime}\right)^{2} \text { with } \gamma>0, \zeta \geq 0 \\
K_{3}\left(\mathbf{x}, \mathbf{x}^{\prime}\right) &=\left(\zeta+\gamma \mathbf{x}^{T} \mathbf{x}^{\prime}\right)^{3} \text { with } \gamma>0, \zeta \geq 0 \\
& \vdots \\
K_{Q}\left(\mathbf{x}, \mathbf{x}^{\prime}\right) &=\left(\zeta+\gamma \mathbf{x}^{T} \mathbf{x}^{\prime}\right)^{Q} \text { with } \gamma>0, \zeta \geq 0
\end{aligned}\]
其中 \(K_1\) : 代表了正常的内积, 叫做线性核。一定要记住线性先行。
高斯核函数(Gaussian Kernel)
上述的多项式核函数都是有限维度的,那么现在使用核技巧避免了对映射空间的依赖,是否存在拥有无限维度(infinite dimensional)或者说最有力(most powerful)的映射函数 \(\Phi\) 呢?——引出高斯核函数
\[\begin{aligned}
K\left(x, x^{\prime}\right) & =\exp \left(-\left(x-x^{\prime}\right)^{2}\right) \\
&=\exp \left(-(x)^{2}\right) \exp \left(-\left(x^{\prime}\right)^{2}\right) \exp \left(2 x x^{\prime}\right) \\
&{\mathop{\Longrightarrow}\limits^{\text { Taylor }}} \exp \left(-(x)^{2}\right) \exp \left(-\left(x^{\prime}\right)^{2}\right)\left(\sum_{i=0}^{\infty} \frac{\left(2 x x^{\prime}\right)^{i}}{i !}\right) \\
&=\sum_{i=0}^{\infty}\left(\exp \left(-(x)^{2}\right) \exp \left(-\left(x^{\prime}\right)^{2}\right) \sqrt{\frac{2^{i}}{i !}} \sqrt{\frac{2^{i}}{i !}}(x)^{i}\left(x^{\prime}\right)^{i}\right.\\
&=\Phi(x)^{T} \Phi\left(x^{\prime}\right)
\end{aligned}
\]
这时便有了无限维的映射函数:
\[\Phi(x)=\exp \left(-x^{2}\right) \cdot\left(1, \sqrt{\frac{2}{1 !}} x, \sqrt{\frac{2^{2}}{2 !}} x^{2}, \ldots\right)
\]
所以通用的高斯核函数(Gaussian Kernel)可以写为:
\[K\left(\mathbf{x}, \mathbf{x}^{\prime}\right)=\exp \left(-\gamma\left\|\mathbf{x}-\mathbf{x}^{\prime}\right\|^{2}\right) \text { with } \gamma>0
\]
所以拥有高斯核的高斯支持向量机(Gaussian SVM)的表达式如下:
\[\begin{aligned}
g_{\mathrm{svm}}(\mathbf{x}) &=\operatorname{sign}\left(\sum_{\mathrm{SV}} \alpha_{n} y_{n} K\left(\mathrm{x}_{n}, \mathbf{x}\right)+b\right) \\
&=\operatorname{sign}\left(\sum_{\mathrm{SV}} \alpha_{n} y_{n} \exp \left(-\gamma\left\|\mathbf{x}-\mathbf{x}_{n}\right\|^{2}\right)+b\right)
\end{aligned}
\]
又叫做径向基函数核(Radial Basis Function (RBF) kernel)。其中 Radial 代表了类似 Gaussian 这样由中心向外放射的函数,而 Basis 代表了线性组合。
值得注意的是当 \(\gamma\) 过大时,会导致过拟合
不同核函数的优缺(Comparison of Kernels)
- 线性核(Linear Kernel):important and basic
- 优点:安全(Linear first),快速(使用Special QP 求解很快),可解释性强(\(\mathbf{w}\) 和 \(SVs\) 可以代表一些东西)。
- 缺点:有局限性,只适用于线性可分的数据
- 多项式核(Polynomial Kernel):perhaps small-Q only(尽量使用低阶次的)
- 优点:阶次(Q)可控,解决非线性
- 缺点:数值计算难以处理(高阶次时),且三个参数 \(( \gamma , \zeta , Q )\) 难以选择。
- 高斯核(Gaussian Kernel):one of most popular but be used with care
- 优点:比线性核和多项式核有更高的空间,且数值计算好处理(bounded),只需要选择一个参数。
- 缺点:比线性计算慢,\(\mathbf{w}\) 的可解释性差,比线性计算的更慢,太有力(too powerful)了容易导致过拟合(overfit)。
其他有效的核(Other Valid Kernels)
一个核函数有效的充分必要条件是: Mercer’s condition
- 对称(symmetric)
- 矩阵\(K\)总是半正定的,矩阵\(K\)的组成为:\(k _ { i j } = K \left( \mathbf { x } _ { i } , \mathbf { x } _ { j } \right)\),即
\[\begin{aligned}K & = \left[ \begin{array} { c c c c } \boldsymbol { \Phi } \left( \mathbf { x } _ { 1 } \right) ^ { T } \boldsymbol { \phi } \left( \mathbf { x } _ { 1 } \right) & \boldsymbol { \Phi } \left( \mathbf { x } _ { 1 } \right) ^ { T } \boldsymbol { \Phi } \left( \mathbf { x } _ { 2 } \right) & \dots & \mathbf { \Phi } \left( \mathbf { x } _ { 1 } \right) ^ { T } \boldsymbol { \Phi } \left( \mathbf { x } _ { N } \right) \\ \boldsymbol { \Phi } \left( \mathbf { x } _ { 2 } \right) ^ { T } \boldsymbol { \phi } \left( \mathbf { x } _ { 1 } \right) & \boldsymbol { \Phi } \left( \mathbf { x } _ { 2 } \right) ^ { T } \boldsymbol { \Phi } \left( \mathbf { x } _ { 2 } \right) & \dots & \boldsymbol { \Phi } \left( \mathbf { x } _ { 2 } \right) ^ { T } \boldsymbol { \phi } \left( \mathbf { x } _ { N } \right) \\ \cdots & \cdots & \cdots & \cdots \\ \boldsymbol { \Phi } \left( \mathbf { x } _ { N } \right) ^ { T } \Phi \left( \mathbf { x } _ { 1 } \right) & \boldsymbol { \Phi } \left( \mathbf { x } _ { N } \right) ^ { T } \Phi \left( \mathbf { x } _ { 2 } \right) & \ldots & \boldsymbol { \Phi } \left( \mathbf { x } _ { N } \right) ^ { T } \Phi \left( \mathbf { x } _ { N } \right) \end{array} \right] \\
&= { \left[ \begin{array} { l l l l } \mathbf { z } _ { 1 } & \mathbf { z } _ { 2 } & \ldots & \mathbf { z } _ { N } \end{array} \right] ^ { T } \left[ \begin{array} { l l l l } \mathbf { z } _ { 1 } & \mathbf { z } _ { 2 } & \ldots & \mathbf { z } _ { N } \end{array} \right] } \\
&= \mathrm { ZZ } ^ { T } \text { must always be positive semi-definite } \end{aligned}
\]
软间隔支持向量机(Soft-Margin SVM)
在之前介绍的都是硬间隔支持向量机,不允许存在分类错误的状况(在噪声存在的情况下)。这里结合 Pocket 算法,对于分类错误的样本点实施以惩罚。
这里引入系数 \(C\),用于权衡大间隔和噪声容忍度(large margin & noise tolerance)。
\[\begin{array} { l l } \min _ { b , w } & \frac { 1 } { 2 } \mathbf { w } ^ { \top } \mathbf { w } + C \cdot \sum _ { n = 1 } ^ { N } \left[\kern-0.25em\left[ y _ { n } \neq \operatorname { sign } \left( \mathbf { w } ^ { \top } \mathbf { z } _ { n } + b \right) \right] \kern-0.25em \right] \\ \text { s.t. } & y _ { n } \left( \mathbf { w } ^ { T } \mathbf { z } _ { n } + b \right) \geq 1 \text { for correct } n \\ & y _ { n } \left( \mathbf { w } ^ { T } \mathbf { z } _ { n } + b \right) \geq - \infty \text { for incorrect } n \end{array}
\]
可以进一步写为
\[\begin{array} { l l } \min _ { b , w } & \frac { 1 } { 2 } \mathbf { w } ^ { T } \mathbf { w } + C \cdot \sum _ { n = 1 } ^ { N } \left[ \kern-0.25em \left[y _ { n } \neq \operatorname { sign } \left( \mathbf { w } ^ { T } \mathbf { z } _ { n } + b \right) \right] \kern-0.25em \right]\\ \text { s.t. } & y _ { n } \left( \mathbf { w } ^ { T } \mathbf { z } _ { n } + b \right) \geq 1 - \infty \cdot \left[ \kern-0.25em \left[ y _ { n } \neq \operatorname { sign } \left( \mathbf { w } ^ { T } \mathbf { z } _ { n } + b \right) \right] \kern-0.25em \right] \end{array}
\]
但是值得注意的是 \(\left[ \kern-0.15em \left[ \right]\kern-0.15em \right]\) 操作是非线性的,所以无法使用QP求解器求解。所以这里想到计算边距对的违反程度(margin violation) 而不是错误的个数(error count),从而转换为二次项:
\[\begin{aligned} \min _ { b , \mathbf { w } , \xi } & \frac { 1 } { 2 } \mathbf { w } ^ { T } \mathbf { w } + C \cdot \sum _ { n = 1 } ^ { N } \xi _ { n } \\ \text { s.t. } & y _ { n } \left( \mathbf { w } ^ { T } \mathbf { z } _ { n } + b \right) \geq 1 - \xi _ { n } \text { and } \xi _ { n } \geq 0 \text { for all } n \end{aligned}
\]
可以看出本问题是一个二次规划问题 \(\mathrm { QP } \text { with } \tilde { d } + 1 + N \text { variables, } 2 N \text { constraints }\),为了摆脱对 \(\tilde { d }\) 的依赖,现求解其对偶问题。
拉格朗日对偶问题(Lagrange Dual Problem)
首先将其转换为无约束最优化问题:写出其拉格朗日方程(Lagrange Function),其中 \(\alpha_{n},\beta_n\) 为拉格朗日乘数(Lagrange Multiplier)。
\[\begin{aligned}
\mathcal { L } ( b , \mathbf { w } , \boldsymbol { \xi } , \alpha , \boldsymbol { \beta } ) = & \frac { 1 } { 2 } \mathbf { w } ^ { \top } \mathbf { w } + C \cdot \sum _ { n = 1 } ^ { N } \xi _ { n } \\ & + \sum _ { n = 1 } ^ { N } \alpha _ { n } \cdot \left( 1 - \xi _ { n } - y _ { n } \left( \mathbf { w } ^ { T } \mathbf { z } _ { n } + b \right) \right) \\ &+ \sum _ { n = 1 } ^ { N } \beta _ { n } \cdot \left( - \xi _ { n } \right)
\end{aligned}
\]
现在求取拉格朗日的对偶问题(Lagrange dual):
\[\max _ { \alpha _ { n } \geq 0 , \beta _ { n } \geq 0 } \left( \min _ { b , \mathbf { w } , \xi } \mathcal { L } ( b , \mathbf { w } , \boldsymbol { \xi } , \boldsymbol { \alpha } , \boldsymbol { \beta } ) \right) \\
\Longrightarrow \max _ { \alpha _ { n } \geq 0 , \beta _ { n } \geq 0 } \left( \min _ { b , \mathbf { w } , \xi } \frac { 1 } { 2 } \mathbf { w } ^ { \top } \mathbf { w } + C \cdot \sum _ { n = 1 } ^ { N } \xi _ { n } + \sum _ { n = 1 } ^ { N } \alpha _ { n } \cdot \left( 1 - \xi _ { n } - y _ { n } \left( \mathbf { w } ^ { T } \mathbf { z } _ { n } + b \right) \right) + \sum _ { n = 1 } ^ { N } \beta _ { n } \cdot \left( - \xi _ { n } \right) \right)
\]
求解对偶 Soft-Margin SVM
与硬间隔支持向量机相似:
由于里面优化问题为无约束最优化问题,所以其最优解满足:
\[\frac { \partial \mathcal { L } } { \partial \xi _ { n } } = 0 = C - \alpha _ { n } - \beta _ { n }
\]
即 \(\beta _ { n } = C - \alpha _ { n },0 \leq \alpha _ { n } \leq C\) 代入原问题有,可以得出:
\[\max _ { \alpha _ { n } \geq 0 , \beta _ { n } \geq 0 } \left( \min _ { b , \mathbf { w } , \xi } \frac { 1 } { 2 } \mathbf { w } ^ { \top } \mathbf { w } + C \cdot \sum _ { n = 1 } ^ { N } \xi _ { n } + \sum _ { n = 1 } ^ { N } \alpha _ { n } \cdot \left( 1 - \xi _ { n } - y _ { n } \left( \mathbf { w } ^ { T } \mathbf { z } _ { n } + b \right) \right) + \sum _ { n = 1 } ^ { N } \beta _ { n } \cdot \left( - \xi _ { n } \right) \right) \\
\Longrightarrow \max _ { \alpha _ { n } \geq 0 , \beta _ { n } \geq 0 } \left( \min _ { b , \mathbf { w } , \xi } \frac { 1 } { 2 } \mathbf { w } ^ { \top } \mathbf { w } + \sum _ { n = 1 } ^ { N } \alpha _ { n } \cdot \left( 1 - y _ { n } \left( \mathbf { w } ^ { T } \mathbf { z } _ { n } + b \right) \right) \right)
\]
至此可以看出其内部问题与硬间隔支持向量机的内部问题一样:
\[\frac { \partial \mathcal { L } } { \partial b } = 0 \Rightarrow
\sum _ { n = 1 } ^ { N } \alpha _ { n } y _ { n } = 0 \\
\frac { \partial \mathcal { L } } { \partial w _ { i } } = 0 \Rightarrow
\mathbf { w } = \sum _ { n = 1 } ^ { N } \alpha _ { n } y _ { n } \mathbf { z } _ { n }
\]
所以与硬间隔支持向量机不同地方是限制条件中 \(\alpha_n\) 的上限(upper bound)改变了:
\[\begin{aligned}
\min _{\alpha} \quad & \frac{1}{2} \sum_{n=1}^{N} \sum_{m=1}^{N} \alpha_{n} \alpha_{m} y_{n} y_{m} \mathbf{z}_{n}^{T} \mathbf{z}_{m}-\sum_{n=1}^{N} \alpha_{n} \\
\text {subject to} \quad & \sum_{n=1}^{N} y_{n} \alpha_{n}=0 \\
& 0 \leq \alpha_{n} \leq C, \text { for } n=1,2, \ldots, N
\end{aligned}
\]
可以看出这是一个QP问题带有 \(N\) 个变量和 \(2N+1\) 个限制条件。
核软间隔支持向量机算法(Kernel Soft-Margin SVM Algorithm)的具体实现步骤为:
- \(q_{n, m}=y_{n} y_{m} K\left(\mathbf{x}_{n}, \mathbf{x}_{m}\right) ; \mathbf{p}=-\mathbf{1}_{N} ;(\mathrm{A}, \mathbf{c})\) for equ./bound constraints
- \(\alpha \leftarrow \mathrm{QP}\left(\mathrm{Q}_{\mathrm{D}}, \mathrm{p}, \mathrm{A}, \mathrm{c}\right)\)
- \(b \leftarrow
y _ { s } - \sum \limits_ { \mathrm { SV } \text { indices } n } \alpha _ { n } y _ { n } K \left( \mathbf { x } _ { n } , \mathbf { x } _ { s } \right)\)
- return SVs and their \(\alpha_{n}\) as well as \(b\) such that for new \(\mathbf{x}\)
\[g_{\mathrm{svm}}(\mathbf{x})=\operatorname{sign}\left(\underset{\text { SV indices } n}{\sum} \alpha_{n} y_{n} K\left(\mathbf{x}_{n}, \mathbf{x}\right)+b\right)
\]
其中 \(b\) 的获取是通过KKT条件中的第四条,\(\alpha _ { n } \left( 1 - \xi_n - y _ { n } \left( \mathbf { w } ^ { T } \mathbf { z } _ { n } + b \right) \right) = 0, (C - \alpha_n)\xi_n = 0\) 当 \(0< \alpha_n < C\) 时,\(\xi_n = 0\),\(b=y_{n}-\mathbf{w}^{T} \mathbf{z}_{n}\),在前文推导过,\(\alpha_n\) 不可能全为零,当然同理可以推导不可能全为 \(C\),但是不能保证 \(\alpha_n\) 只能为 零 或 \(C\)。所以如果不存在 \(\alpha_s \in (0,C)\) ,那么需要对 \(b\) 进行条件限制后求解,当然大部分情况下是存在的。
\(\alpha_n\) 的物理意义(Physical Meaning)
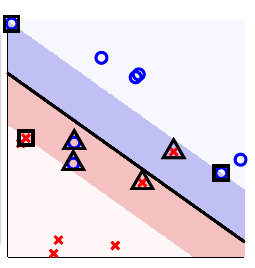
![在这里插入图片描述]()
\(\square\) 代表了 free SV \(\left( 0 < \alpha _ { n } < C \right)\) 即 \(\xi _ { n } = 0,\Rightarrow\) on fat boundary, locates \(b\)。
\(\Delta\) 代表了 bounded SV \(\left( \alpha _ { n } = C \right)\) 即 \(\xi _ { n } = \text{violation amount},\Rightarrow\) ‘violate’/on fat boundary
其他无符号的不是支持向量 \(\left(\alpha _ { n } = 0\right)\) 即 \(\xi _ { n } = 0,\Rightarrow\) ‘away from’/on fat boundary
也就是说 \(b\) 需要在有 free SV 的情况下才能求解。当然 \(\alpha_n\) 也可以用于数据分析两种支持向量的数量。
模型选择(Model Selection)
交叉验证(Cross Validation)
\(E _ { \mathrm { cv } } ( C , \gamma )\) 是一种非平滑的函数,很难优化,所以 V折交叉验证(V-fold cross validation )经常用于模型选择,方法是通过对 不同的 \(( C , \gamma )\) 的网格值(grid values,不同数值组合)测试交叉验证误差 \(E _ { \text {cv} }\) 的大小,选取最优的模型。
交叉验证误差:对于软间隔 SVM 是非常流行的评价标准。
支持向量的个数(number of SV)
值得注意的是支持向量的个数(#SV)可用于表达 \(E _ { \text {loocv} }\) (Leave one out cross validation)的一种上限:
\[E _ { \text {loocv } } \leq \frac { \# \mathrm { SV } } { N }
\]
下面进行证明,在证明之前,先回顾一下 SVM 的求取过程,即非支持向量对于最佳模型是无影响的:
\[\begin{array} { l } \text { for } \left( \mathbf { x } _ { N } , y _ { N } \right) : \text { if optimal } \alpha _ { N } = 0 \text { (non-SV) } \\ \Longrightarrow \left( \alpha _ { 1 } , \alpha _ { 2 } , \ldots , \alpha _ { N - 1 } \right) \text { still optimal when leaving out } \left( \mathbf { x } _ { N } , y _ { N } \right) \end{array}
\]
并且每一个样本的误差均小于等于零,其非支持向量的误差为零,也就是说:
\[\begin{aligned} e _ { \text {non-SV } } & = \operatorname { err } \left( g ^ { - } , \text {non-SV } \right) \\ & = \operatorname { err } ( g , \text { non-SV } ) = 0 \\ e _ { S V } & \leq 1 \end{aligned}
\]
所以虽然只是上限,但是当交叉验证非常耗时时,支持向量的个数经常用于估计模型的安全性,支持向量的个数越多越容易过拟合。方法是通过对 不同的 \(( C , \gamma )\) 的网格值(grid values,不同数值组合)测试支持向量(CV)的个数,选取最优的模型。
软间隔实用工具有:LIBLINEAR(线性的),LIBSVM(非线性的)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号