机器学习技法 之 神经网络（Neural Network）

动机（Motivation）

感知机的线性融合（Linear Aggregation of Perceptrons）

中文中的感知器或感知机均指的是Perceptron 。

将 Perceptrons 作为 Linear Aggregation 的基模型，搭配方式的网络结构图图如下所示：

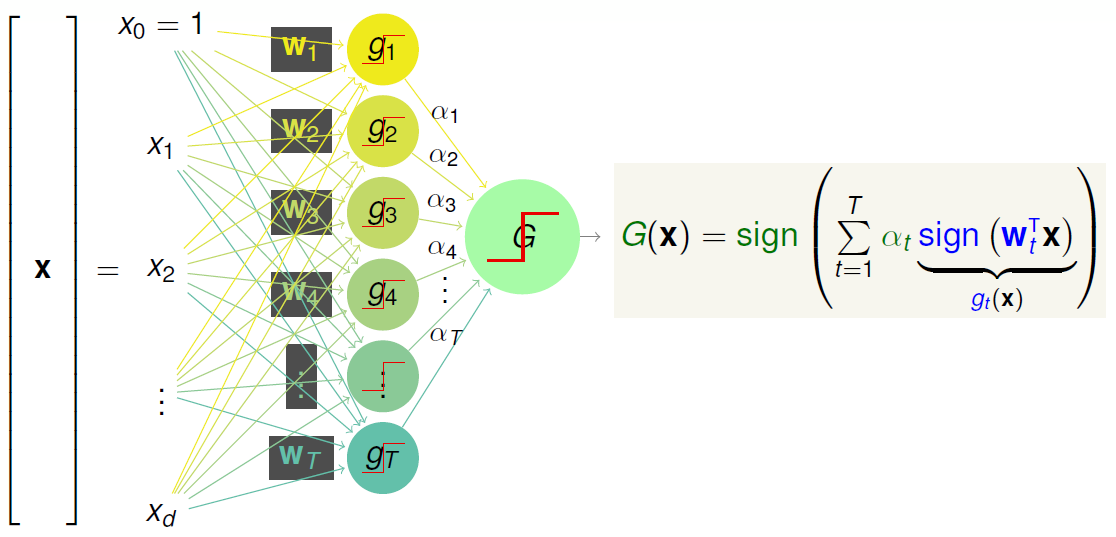
可以看出这里使用了两层的权重 \(\mathbf{w}_t\) 和 \(\alpha\)，和两层的 sign 函数分别在 \(g_t\) 和 \(G\)。那这个模型 \(G\) 可以实现什么样子的边界（boundary can G implement）呢。

逻辑操作（Logic Operations with Aggregation）

首先来看一下如何实现逻辑与的操作呢？

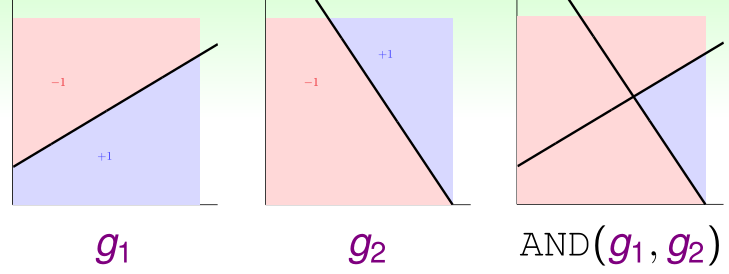
假设负样本对应 FALSE ，同时正样本对应 TRUE。那么在二维平面的与操作对应的图形展示如上图所示，那么实现该功能的感知器的线性融合具体实现网络图为：

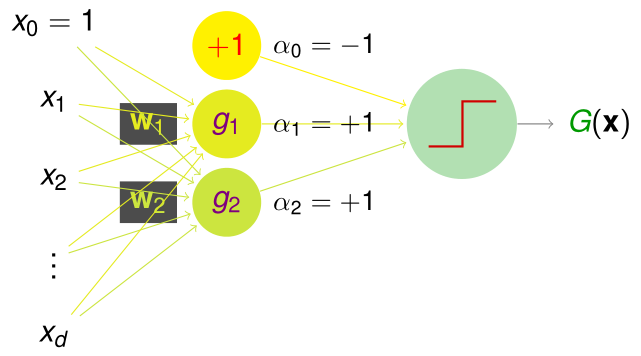
那么该网络实现的功能函数为：

\[G ( \mathbf { x } ) = \operatorname { sign } \left( - 1 + g _ { 1 } ( \mathbf { x } ) + g _ { 2 } ( \mathbf { x } ) \right) \]

也就是说当 \(g _ { 1 } ( \mathbf { x } ) = g _ { 2 } ( \mathbf { x } ) = + 1 ( \mathrm { TRUE } )\) 时，\(G ( \mathbf { x } ) = + 1 ( \mathrm { TRUE } )\)。其他情况下：\(G ( \mathbf { x } ) = - 1 ( \mathrm { FALSE } )\)。

即 \(G \equiv \operatorname { AND } \left( g _ { 1 } , g _ { 2 } \right)\)，实现了与操作，当然或操作以及非操作也可同理实现。

强大但有局限性（Powerfulness and Limitation）

先说它的 Powerfulness ，以下图为例：

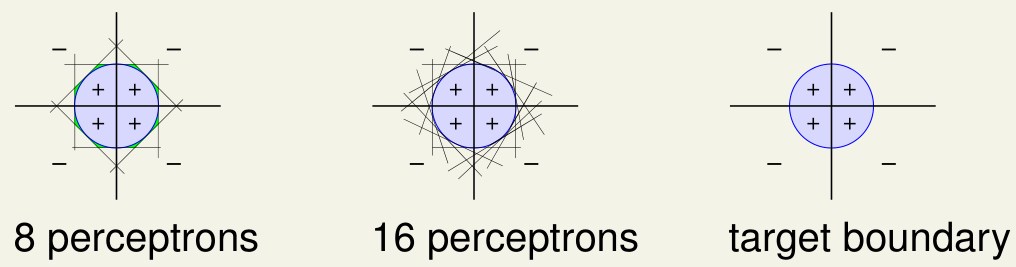
如果目标边界是一个圆形，园内为正样本，圆外为负样本。当然单个样本是无法实现，这样的样本分类的，但是随着 Perceptrons 的增加，边界越来越光滑并趋于一个目标边界（target boundary 圆形）。

实际上如果有足够多的 Perceptrons ，可以组成任意形状的光滑凸多边形，当然要注意 \(d _ { \mathrm { vc } } \rightarrow \infty\)，即 Perceptrons 过多导致的模型复杂度过高。

但是这个强大的模型，是无法实现 XOR（Exclusive OR）操作的。

多层感知机（Multi-Layer Perceptrons: Basic Neural Network）

对于不可分的数据一般的操作都是使用多次转换，那么这里如果实现异或操作呢，那就是先使用与操作进行转换，再使用或操作进行转换：

\[\mathrm { XOR } \left( g _ { 1 } , g _ { 2 } \right) = \operatorname { OR } \left( \operatorname { AND } \left( - g _ { 1 } , g _ { 2 } \right) , \operatorname { AND } \left( g _ { 1 } , - g _ { 2 } \right) \right) \]

具体实现的网络结构图如下：

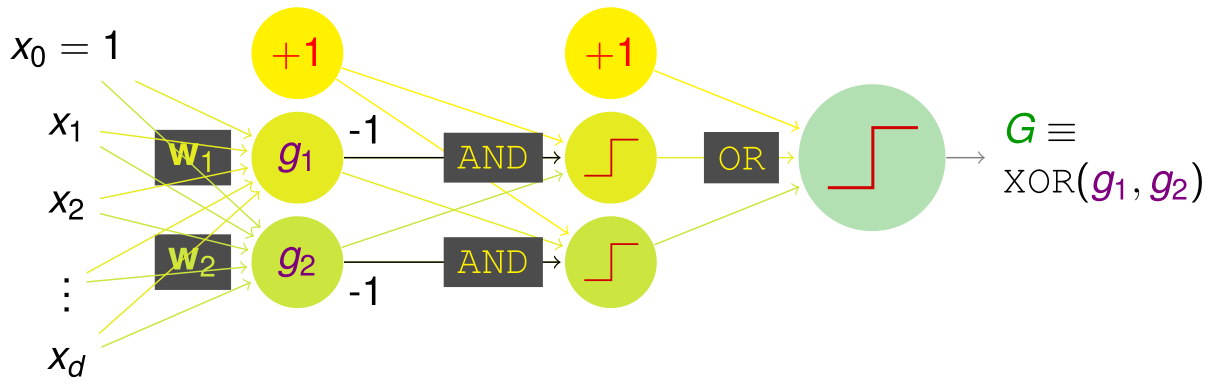
单个感知机很简单、有局限性，所以使用 aggregation of perceptrons 建立单层的感知机，单层感知机也存在自己的局限性，所以由此提出了多层感知机的概念。

perceptron (simple) ⇒ aggregation of perceptrons (powerful) ⇒ multi-layer perceptrons (more powerful)

多层感知机实际上来源于生物神经元（Biological Neurons），是一个仿生物模型（bio-inspired model），所以也称之为神经网络。

神经网络输出端假设函数（Neural Network Hypothesis: Output）

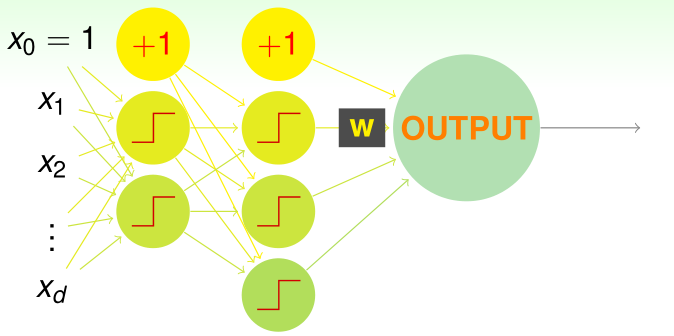
对于上述的两层神经网络，可以写出 OUTPUT 端的分数值为：

\[s = \mathbf { w } ^ { T } \phi ^ { ( 2 ) } \left( \phi ^ { ( 1 ) } ( \mathbf { x } ) \right) \]

可以看出输出端是一个简单的线性模型，所以下面这三种原来学过的线性模型都可以用在这里：

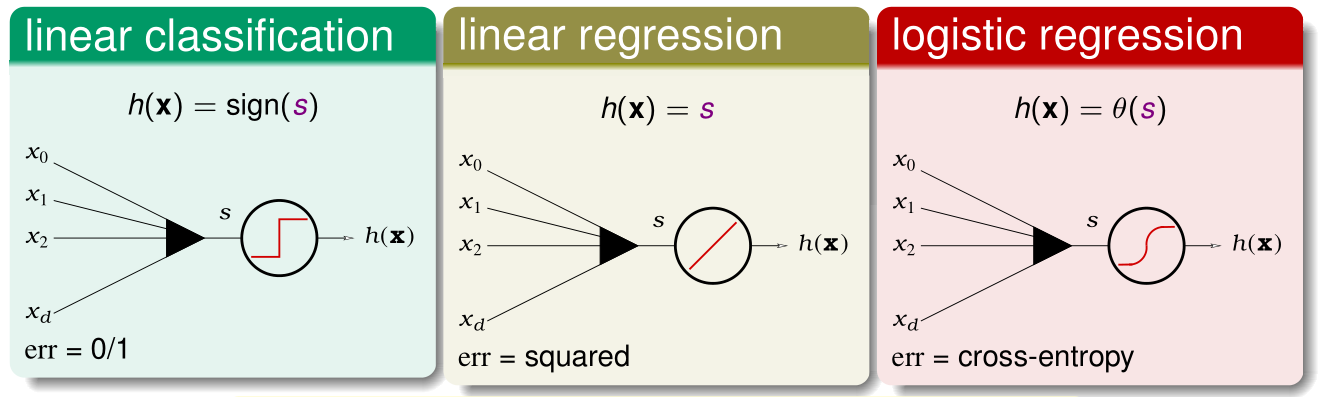
本文中套用的是 Linear Regression（with squared error），进行讲解的。当然也可以延伸到其他线性模型。

神经网络隐含层假设函数（Neural Network Hypothesis: Transformation）

隐含层实际上就是中间转换层。在前文中，中间转换层均适用的是 Perceptron。但是其使用的 sign 的输出值是一个离散值，难以优化权值 \(\mathbf{w}\)。同时如果使用 linear，那么整个神经网络也是线性的，那么用处不大（less useful）。

比较流行的是 tanh（Hyperbolic Tangent，双曲正切函数），其数学表达如下：

\[\begin{aligned} \tanh ( s ) & = \frac { \exp ( s ) - \exp ( - s ) } { \exp ( s ) + \exp ( - s ) } \\ & = 2 \theta ( 2 s ) - 1 \end{aligned} \]

三种曲线如下图所示：

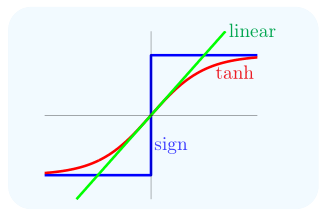
可以看出 tanh 是平滑曲线，易于优化，并且更接近于生物神经元。在本文中便以 tanh 作为 transformation function。

那有了输出端假设函数和隐含层的假设函数，原来的神经网络问题便可以转换为下图的结构：

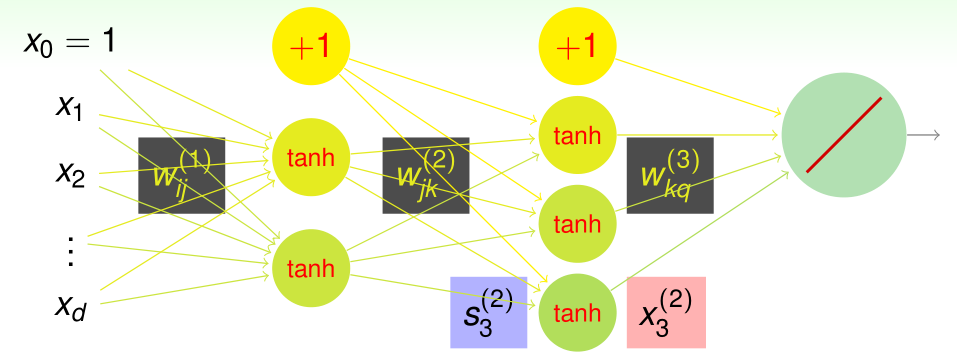
那么现在做如下定义：

每一层神经元（Node）的个数由 \(d ^ { ( \ell ) }\) 表示，那么从输入（0层）到输出（L层）的由个数表达的连接方式为：

\[d ^ { ( 0 ) } - d ^ { ( 1 ) } - d ^ { ( 2 ) } \ldots - d ^ { ( L ) } \]

权重的表示比较复杂，\(w^{ ( \ell ) }_{ij}\) 表示的是由第 \(\ell-1\) 层第 \(i\) 个神经元向第 \(\ell\) 层第 \(j\) 个神经元进行传输时所乘的权重：

\[w^{ ( \ell ) }_{ij} : \left\{ \begin{array} { l l } 1 \leq \ell \leq L & \text { layers } \\ 0 \leq i \leq d ^ { ( \ell - 1 ) } & \text { inputs } \\ 1 \leq j \leq d ^ { ( \ell ) } & \text { outputs } \end{array} \right. \]

分数 \(s _ { j } ^ { ( \ell ) }\) 表示的是第 \(\ell\) 层的第 \(j\) 个神经元的输入值：

\[\text { score } s _ { j } ^ { ( \ell ) } = \sum _ { i = 0 } ^ { d ^ { ( \ell - 1 ) } } w _ { i j } ^ { ( \ell ) } x _ { i } ^ { ( \ell - 1 ) } \]

转换值 \(x _ { j } ^ { ( \ell ) }\) 表示的是第 \(\ell\) 层的第 \(j\) 个神经元的输出值

\[\text { transformed } x _ { j } ^ { ( \ell ) } = \left\{ \begin{array} { l l } \tanh \left( s _ { j } ^ { ( \ell ) } \right) & \text { if } \ell < L \\ s _ { j } ^ { ( \ell ) } & \text { if } \ell = L \end{array} \right. \]

那么现在的特征（属性）\(\mathbf{x}\) 将被作为 \(\mathbf{x}^{(0)}\)，通过隐含层（hidden layers）获得 \(x _ { j } ^ { ( \ell ) }\)，最终得到输出层\(x _ { 1} ^ { ( L) }\)。

实际上每一层都是在从数据中学习转换模式（transformation to be learned from data），将每一层的转换函数写出：：

\[\phi ^ { ( \ell ) } ( \mathbf { x } ) = \tanh \left( \left[ \begin{array} { c } \sum _ { i = 0 } ^ { d^{( \ell )} } w _ { i 1 } ^ { ( \ell ) } x _ { i } ^ { ( \ell - 1 ) } \\ \vdots \end{array} \right] \right) \]

可以看出该转换函数是将输入的 \(\mathbf{x}\) 与权重向量做内积，然后使用 tanh 函数转换输出，什么时候两者的值最大呢？在机器学习可行性分析时用到过，两个向量在不考虑向量长度时，两个向量越接近，角度越小，那么内积越大。所以这个函数一定程度上表示两者的模式是否匹配或接近（whether x ‘matches’ weight vectors in pattern）。

所以神经网络（NNet）实际上就是通过层间的连接权重来进行模式提取的过程（pattern extraction with layers of connection weights）。

反向传播算法（Backpropagation Algorithm）

那现在的问题是如何学习权重 \(\left\{ w _ { i j } ^ { ( \ell ) } \right\}\)，使得 \(\text { minimize } E _ { \text {in } } \left( \left\{ w _ { i j } ^ { ( \ell ) } \right\} \right)\)。

因为只有输出端的预测误差，所以基本的思路是，从输出端出发，从输出端向后层层反馈。

输出端的预测误差：

\[e _ { n } = \left( y _ { n } - \operatorname { NNet } \left( \mathbf { x } _ { n } \right) \right) ^ { 2 } \]

最后一层的权值优化怎么实现呢，因为有预测误差，那么通过（随机）梯度下降法便可以实现优化目标。

首先应该求取 \(\frac { \partial e _ { n } } { \partial w _ { i j } ^ { ( l ) } }\)，令其为零。求法如下：

先将预测误差展开为显式：

\[e _ { n } = \left( y _ { n } - \mathrm { N } \operatorname { Net } \left( \mathbf { x } _ { n } \right) \right) ^ { 2 } = \left( y _ { n } - s _ { 1 } ^ { ( L ) } \right) ^ { 2 } = \left( y _ { n } - \sum _ { i = 0 } ^ { d ^ { ( L - 1 ) } } w _ { i 1 } ^ { ( L ) } x _ { i } ^ { ( L - 1 ) } \right) ^ { 2 } \]

对于最后一层（Output Layer）的梯度值求取：

\[\begin{aligned} & \frac { \partial e _ { n } } { \partial w _ { i 1 } ^ { ( L ) } } \\ = & \frac { \partial e _ { n } } { \partial s _ { 1 } ^ { ( L ) } } \cdot \frac { \partial s _ { 1 } ^ { ( L ) } } { \partial w _ { i 1 } ^ { ( L ) } } \\ = & - 2 \left( y _ { n } - s _ { 1 } ^ { ( L ) } \right) \cdot \left( x _ { i } ^ { ( L - 1 ) } \right) \end{aligned} \]

对于中间的隐含层的梯度值求取：

\[\begin{aligned} & \frac { \partial e _ { n } } { \partial w _ { i j } ^ { ( \ell ) } } \\ = & \frac { \partial e _ { n } } { \partial s _ { j } ^ { ( \ell ) } } \cdot \frac { \partial s _ { j } ^ { ( \ell ) } } { \partial w _ { i j } ^ { ( \ell ) } } \\ = & \delta _ { j } ^ { ( \ell ) } \cdot \left( x _ { i } ^ { ( \ell - 1 ) } \right) \end{aligned} \]

由于这里中间层的 \(\frac { \partial e _ { n } } { \partial s _ { j } ^ { ( \ell ) } }\) 不好求取，所以暂时由 \(\delta _ { j } ^ { ( \ell ) }\) 代替，当然输出层的 \(\delta _ { 1 } ^ { ( L) } = - 2 \left( y _ { n } - s _ { 1 } ^ { ( L ) } \right)\)。

下面进行 \(\delta _ { j } ^ { ( \ell ) }\) 的实际值计算：

根据网络结构的传递，可以写出如下的值传递关系：

\[s _ { j } ^ { ( \ell ) } \stackrel { \tanh } { \Longrightarrow } x _ { j } ^ { ( \ell ) } \stackrel { w _ { j k } ^ { ( \ell + 1 ) } } { \Longrightarrow } \left[ \begin{array} { c } s _ { 1 } ^ { ( \ell + 1 ) } \\ \vdots \\ s _ { k } ^ { ( \ell + 1 ) } \\ \vdots \end{array} \right] \Longrightarrow \cdots \Longrightarrow e _ { n } \]

这样的话，便可以通过 \(\delta _ { j } ^ { ( \ell+1 ) }\) 计算 \(\delta _ { j } ^ { ( \ell) }\)。

\[\begin{aligned} \delta _ { j } ^ { ( \ell ) } = \frac { \partial e _ { n } } { \partial s _ { j } ^ { ( \ell ) } } & = \sum _ { k = 1 } ^ { d ^ { ( \ell + 1 ) } } \frac { \partial e _ { n } } { \partial s _ { k } ^ { ( \ell + 1 ) } } \frac { \partial s _ { k } ^ { ( \ell + 1 ) } } { \partial x _ { j } ^ { ( \ell ) } } \frac { \partial x _ { j } ^ { ( \ell ) } } { \partial s _ { j } ^ { ( \ell ) } } \\ & = \sum _ { k } \left( \delta _ { k } ^ { ( \ell + 1 ) } \right) \left( w _ { j k } ^ { ( \ell + 1 ) } \right) \left( \tanh ^ { \prime } \left( s _ { j } ^ { ( \ell ) } \right) \right) \end{aligned} \]

由于最后一个 \(\delta _ { j } ^ { ( \ell) }\) 可以求得，即\(\delta _ { 1 } ^ { ( L ) }\)。那么从后向前可以计算出全部的 \(\delta _ { j } ^ { ( \ell) }\)。

由此得出经典的反向传播算法（Backpropagation (Backprop) Algorithm）。

\[\begin{aligned} & \text { initialize all weights } w _ { i j } ^ { ( \ell ) } \\ & \text { for } t = 0,1 , \ldots , T \\ & \qquad\text { (1) } \text { Stochastic: randomly pick } n \in \{ 1,2 , \cdots , N \} \\ & \qquad \text { (2) } \text { forward: compute all } x _ { i } ^ { ( \ell ) } \text { with } \mathbf { x } ^ { ( 0 ) } = \mathbf { x } _ { n } \\ &\qquad \text { (3) } \text { backward: compute all } \delta _ { j } ^ { ( \ell ) } \text { subject to } \mathbf { x } ^ { ( 0 ) } = \mathbf { x } _ { n } \\ &\qquad \text { (4) } \text { gradient descent: } w _ { i j } ^ { ( \ell ) } \leftarrow w _ { i j } ^ { ( \ell ) } - \eta x _ { i } ^ { ( \ell - 1 ) } \delta _ { j } ^ { ( \ell ) } \\ &\text { return } g _ { \text {NNET } } ( \mathbf { x } ) = \left( \cdots \tanh \left( \sum _ { j } w _ { j k } ^ { ( 2 ) } \cdot \tanh \left( \sum _ { i } w _ { i j } ^ { ( 1 ) } x _ { i } \right) \right) \right) \end{aligned} \]

实际运用中对于 for 循环中的 1,2,3 步，执行很多次，也就是说不只随机选取一个 \(n\)，而是取多个，计算 \(x _ { i } ^ { ( \ell - 1 ) } \delta _ { j } ^ { ( \ell ) }\) 的平均值，用于第 4 步更新梯度，这样的操作叫 小批量梯度下降法（mini-batch GD），跟随机梯度下降法的区别是每次选取不只一个样本点。

基础的神经网络算法（basic NNet algorithm）: 使用反向传播算法可以有效的计算梯度值（basic NNet algorithm: backprop to compute the gradient efficiently)。

值得注意的是，当且仅当 \(s _ { i } ^ { ( L ) } = 0\) 时有：

\[x _ { i } ^ { ( L ) } = \tanh \left( s _ { i } ^ { ( L ) } \right) = 0 \]

神经网络的优化（Neural Network Optimization）

局部最优（Local Minimum）

通常多层感知机是凹函数（generally non-convex when multiple hidden layers），那么通过使用梯度下降法实现的反向传播算法很难达到全局最优解（global minimum），常常只停留在局部最优解（local minimum）。

当然不同的初始值对应了不同的局部最优解：

\[\text { different initial } w _ { i j } ^ { ( \ell ) } \Longrightarrow \text { different local minimum } \]

那么便可以通过随机的初始值获取到不同的局部最优点来缓和这一缺陷。同时应当注意，当权值过高时，分数也会很高，这就导致使用 tanh 函数的话，其处于平缓的位置（saturate），梯度很小（small gradient）优化速度会很慢，所以这里建议多尝试几个几个随机的小初始权值。

虽然在神经网络的优化很难，但是却很实用。

VC维数（VC Dimension）

神经网络的复杂度如下：

\[d _ { \mathrm { vc } } = O ( V D ) \text { where } V = \# \text { of neurons, } D = \# \text { of weights } \]

所以其优点是当神经元（neurons）足够多时，也就是说 \(V\) 很大，\(d _ { \mathrm { vc } }\) 很大，那么可以用于解决（拟合）任何线性或非线性问题（函数）。但是 \(d _ { \mathrm { vc } }\) 很大时，很可以会出现过拟合问题。

正则化（Regularization）

那么权重衰减（二范数）正则化，也可以用到这里：

\[\text { weight-decay (L2) regularizer } \Omega ( \mathbf { w } ) = \sum \left( w _ { i j } ^ { ( l ) } \right) ^ { 2 } \]

但是这里有一个问题就是在缩小权重时：

大的权重会缩小比较大，小的权重会缩小比较小，类似于对于任何权重都取一半值，那么这样会导致权重永远不可能为零。

\[\text { large weight } \rightarrow \text { large shrink; small weight } \rightarrow \text { small shrink } \]

那么现在想使得权重向量为稀疏（sparse）向量（某些元素值为零）即 \(w _ { i j } ^ { ( l ) } = 0\)，从而有效的降低 \(d _ { \mathrm { vc } }\)，L1 范数正则化是一种解决方案，但是 L1 范数存在不可微的情况，而神经网络又是基于梯度下降法进行优化的，这样的话L1范数不太适合于神经网络。这里提出一种权重消除正则化（weight-elimination regularizer）：

\[\sum \frac { \left( w _ { i j } ^ { ( \ell ) } \right) ^ { 2 } } { 1 + \left( w _ { i j } ^ { ( \ell ) } \right) ^ { 2 } } \]

可以看出利用该正则化方法实现稀疏向量。

早停法（Early Stopping）

梯度下降法实际上是在当前位置（当前权重 \(\mathbf{w}_i\)）的周围搜索最优解（优化后权重 \(\mathbf{w}_{i+1}\)），这一过程类似于下图：

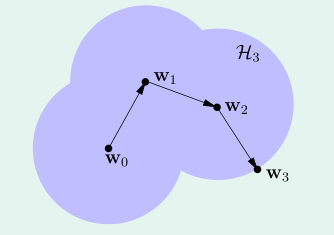
所以随着迭代次数的增加，搜索过的范围越来越广，那么有效的 VC Dimension 也会不断的增加。所以如果迭代次数减少，那么 VC Dimension 也会相应的减小。

回顾一下随着 VC Dimension 增加，\(E_{\text{in}}\) 和 \(E_{\text{out}}\) 的变化曲线：

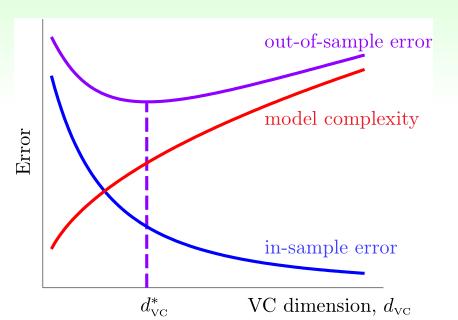
所以最佳的 VC Dimension 在中间，那么最佳的迭代次数也应该在中间，否则很可能出现过拟合问题。当然最佳的迭代次数可以通过 validation 获得。