机器学习技法 之 径向基函数网络（RBF Network）

径向基函数网络（Radial Basis Function Network）：就是将基假设函数进行线性聚合。

径向基函数网络假设函数（RBF Network Hypothesis）

先回顾一下高斯支持向量机（Gaussian SVM）：

\[g _ { \mathrm { svm } } ( \mathbf { x } ) = \operatorname { sign } \left( \sum _ { \mathrm { SV } } \alpha _ { n } y _ { n } \exp \left( - \gamma \left\| \mathbf { x } - \mathbf { x } _ { n } \right\| ^ { 2 } \right) + b \right) \]

其实际上是找出系数 \(\alpha_n\) 将以 \(\mathbf { x } _ { n }\) 为中心的高斯函数进行线性结合。

Gaussian kernel 又叫 Radial Basis Function (RBF) kernel，其中 Radial 指的是这里之关系 \(\mathbf { x }\) 与中心 \(\mathbf { x } _ { n }\) 之间的距离（类似于一种放射线长度求解）。

那么写出高斯支持向量机中的径向基假设函数：

\[g _ { n } ( \mathbf { x } ) = y _ { n } \exp \left( - \gamma \left\| \mathbf { x } - \mathbf { x } _ { n } \right\| ^ { 2 } \right) \]

那么高斯支持向量机可以改写为：

\[g _ { \mathrm { svm} } ( \mathbf { x} ) = \operatorname { sign } \left( \sum _ { \mathrm { SV } } \alpha _ { n } g _ { n } ( \mathbf { x } ) + b \right) \]

可以看出被选择的径向基假设函数的线性结合（linear aggregation of selected radial hypotheses）。

RBF Network 的网络结构示意图如下：

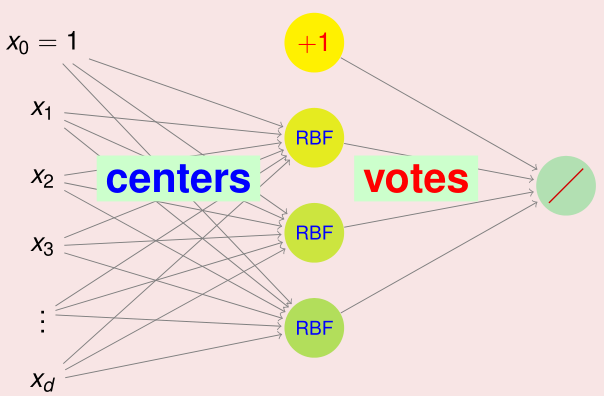
实际上 RBFNet 是 NNet 的一个分支，可见输出层虽然使用的是投票，但是这也是一种线性组合所以与神经网络是一样的。但是隐含层是不同的，在神经网络中使用的是内积加 tanh 输出，而在 RBFNet 中使用的是距离计算加高斯函数。

那么可以写出 RBFNet 的输出假设函数：

\[h ( \mathbf { x } ) = \text { Output } \left( \sum _ { m = 1 } ^ { M } \beta _ { m } \operatorname { RBF } \left( \mathbf { x } , \mu _ { m } \right) + b \right) \]

其中 \(\mu _ { m }\) 是中心点，\(\beta _ { m }\) 是投票系数。

对比与高斯支持向量机：

1. RBF（径向基函数）选择的是高斯函数。
2. Output（输出）选择 sign 做为二分类输出。
3. M 则是支持向量的个数（#SV）。
4. \(\mu _ { m }\) 则是支持向量 \(\mathbf{x}_m\)。
5. \(\beta _ { m }\) 则是通过 SVM Dual 问题求解 \(\alpha_m\) 与 \(y_m\) 的乘积。

不失普遍性的来说：如果要学习径向基函数网络的话，需要选择四个部分：径向基函数 RBF ，输出层假设函数 Output ，中心点的求取 \(\mu _ { m }\) ，投票的系数 \(\beta _ { m }\)。

实际上核技巧实际上就是根据在 \(\mathcal Z\) 空间上的内积求取相似性，比如多项式核：

\[\operatorname { Poly } \left( \mathbf { x } , \mathbf { x } ^ { \prime } \right) = \left( 1 + \mathbf { x } ^ { T } \mathbf { x } ^ { \prime } \right) ^ { 2 } \]

而RBF则是直接通过在 \(\mathcal X\) 空间上的距离求取相似性，一般认为距离越近相似性越大，也就是说距离与相似性单调相关。比如下面这个截断相似性函数：

\[\text { Truncated } \left( \mathbf { x } , \mathbf { x } ^ { \prime } \right) = \left[ \left\| \mathbf { x } - \mathbf { x } ^ { \prime } \right\| \leq 1 \right] \left( 1 - \left\| \mathbf { x } - \mathbf { x } ^ { \prime } \right\| \right) ^ { 2 } \]

而高斯函数则处于他们的交集。

\[\text { Gaussian } \left( \mathbf { x } , \mathbf { x } ^ { \prime } \right) = \exp \left( - \gamma \left\| \mathbf { x } - \mathbf { x } ^ { \prime } \right\| ^ { 2 } \right) \]

相似性是很好的一种特征转换方法。在RBF中则是将中心距离相似性作为特征转换的。其他的相似性函数比如神经元函数或者DNA序列相似性函数：

\[\begin{array} { c } \text { Neuron } \left( \mathbf { x } , \mathbf { x } ^ { \prime } \right) = \tanh \left( \gamma \mathbf { x } ^ { T } \mathbf { x } ^ { \prime } + 1 \right) \\ \text { DNASim } \left( \mathbf { x } , \mathbf { x } ^ { \prime } \right) = \text { EditDistance } \left( \mathbf { x } , \mathbf { x } ^ { \prime } \right) \end{array} \]

RBF网络的训练/学习（RBF Network Learning）

完全RBF网络（Full RBF Network）

如果不考虑 bais ，那么可以写为：

\[h ( \mathbf { x } ) = \operatorname { Output } \left( \sum _ { m = 1 } ^ { M } \beta _ { m } \operatorname { RBF } \left( \mathbf { x } , \boldsymbol { \mu } _ { m } \right) \right) \]

如果令 \(M = N\) 并且每一个 \(\mu _ { m } = \mathbf { x } _ { m }\) 那么这个RBF网络便是完全RBF网络（full RBF Network）。这么做的物理意义是 \(\mathbf { x } _ { m }\) 将通过系数 \(\beta_ { m }\) 来影响每一个与之相似的 \(\mathbf x\)。

那么举例来说，如果使用一个 uniform influence 即 \(\beta _ { m } = 1 \cdot y _ { m }\)，也就是说大家票数一致。

\[g _ { \text {unitorm } } ( \mathbf { x } ) = \operatorname { sign } \left( \sum _ { m = 1 } ^ { N } y _ { \operatorname { m} } \exp \left( - \gamma \left\| \mathbf { x } - \mathbf { x } _ { m } \right\| ^ { 2 } \right) \right) \]

所以说完全RBF网络是一种偷懒的做法，省去了中心向量 \(\mu _ m\) 的求取。

最邻近算法（Nearest Neighbor）

由于高斯函数衰减很快，那么会导致离中心最近的值会获得很大的权重，支配（dominates）投票过程，也就是说具有 “专断权”。所以这个过程更类似于选择一个最大值（最近向量），而不是聚合过程。即：

\[g _ { \text {nbor } } ( \mathbf { x } ) = y _ { m } \text { such that } \mathbf { x } \text { closest to } \mathbf { x } _ { m } \]

所以叫做最邻近模型（nearest neighbor model）。

常用的是 K 邻近模型，根矩 Top k 最邻近的样本进行均值投票（uniformly aggregate k neighbor），虽然很懒（lazy）但是很直观。

无正则化用于插值（Interpolation）

那么如果用于 Regression，那么以平方误差作为误差测量函数，最后的假设函数可以写为：

\[h(\mathbf x) = \left( \sum _ { m = 1 } ^ { N } \beta _ { m } \operatorname { RBF } \left( \mathbf { x } , \mathbf { x } _ { m } \right) \right) \]

可以看出这就是在通过 RBF 映射到的空间上训练线性回归模型

那映射后的数据表示为：

\[\mathbf { z } _ { n } = \left[ \operatorname { RBF } \left( \mathbf { x } _ { n } , \mathbf { x } _ { 1 } \right) , \operatorname { RBF } \left( \mathbf { x } _ { n } , \mathbf { x } _ { 2 } \right) , \ldots , \operatorname { RBF } \left( \mathbf { x } _ { n } , \mathbf { x } _ { N } \right) \right] \]

矩阵 \(\mathrm { Z }\) 由 \(n\) 个 \(\mathbf { z } _ { n }\) 构成，所以矩阵 \(\mathrm { Z }\) 为 \(N\text{(example)} \times N\text{(centers)}\) 的对称方阵（symmetric square matrix），根据线性回归可以写出 \(\beta\) 的最优解：

\[\beta = \left( \mathrm { Z } ^ { T } \mathrm { Z } \right) ^ { - 1 } \mathrm { Z } ^ { T } \mathbf { y } , \text { if } \mathrm { Z } ^ { T } \mathrm { Z } \text { invertible } \]

那么如果全部的 \(\mathbf { x } _ { n }\) 的都是不同的，那么 \(\mathrm { Z }\) （with Gaussian RBF）便是可逆的（invertible）。

又因为 \(\mathrm { Z }\) 是对称方阵，也就是说 \(\mathrm { Z }^T = \mathrm { Z }\)。那么可以化简为：

\[\beta = \left( \mathrm { Z } \mathrm { Z } \right) ^ { - 1 } \mathrm { Z } \mathbf { y } = \mathrm { Z } ^ { - 1 } \mathbf { y } \]

正则化（Regularization）

那么 \(\mathrm { x } _ { 1 }\) 的 RBF的网络输出为：

\[g _ { \mathrm { RBF } } \left( \mathrm { x } _ { 1 } \right) = \boldsymbol { \beta } ^ { T } \mathrm { z } _ { 1 } = \mathbf { y } ^ { T } \mathrm { Z } ^ { - 1 } ( \text {first column of } \mathrm { Z } ) = \mathbf { y } ^ { T } \left[ \begin{array} { l l l l } 1 & 0 & \ldots & 0 \end{array} \right] ^ { T } = y _ { 1 } \]

也就是说 \(g _ { \mathrm { RBF } } \left( \mathrm { x } _ { n } \right) = y _ { n } , \text { i.e. } E _ { \mathrm { in } } \left( g _ { \mathrm { RBF } } \right) = 0\)，那么这样的结果用于精确插值的函数估计（exact interpolation for function approximation）是非常好的，但是在机器学习中便会出现过拟合问题。所以可以加入 Regularization，当然前面学习过岭回归（ridge regression），可以将 regularized full RBFNet \(\beta\) 的求解改写为：

\[\beta = \left( \mathrm { Z } ^ { T } \mathrm { Z } + \lambda \mathrm { I } \right) ^ { - 1 } \mathrm { Z } ^ { T } \mathrm { y } \]

在 kernel ridge regression 中，有一个 \(\mathbf { K }\) 矩阵：

\[\mathrm { Z } = \left[ \text {Gaussian } \left( \mathbf { x } _ { n } , \mathbf { x } _ { m } \right) \right] = \text { Gaussian kernel matrix } \mathbf { K } \]

在 kernel ridge regression 中，\(\beta\) 的求解为：

\[\beta = ( \mathrm { K } + \lambda \mathrm { I } ) ^ { - 1 } \mathrm { y } \]

两者很相近，但是由于正则化的对象不同所以求解公式也不同，在核岭回归中的针对的正则化对象为无限多维的转换。而 RBF 中针对的是有限多维的 \(N\) 维的转换。

K均值算法（k-Means Algorithm）

反观 SVM，实际上并没有使用到全部的 \(\mathbf x_n\) ，而只是用到了支持向量，即 \(M \ll N\)。

\[g _ { \mathrm { svm } } ( \mathbf { x } ) = \operatorname { sign } \left( \sum _ { \mathrm { SV } } \alpha _ { m } y _ { m } \exp \left( - \gamma \left\| \mathbf { x } - \mathbf { x } _ { m } \right\| ^ { 2 } \right) + b \right) \]

也就是通过限制中心的个数和投票的权重来达到正则化的效果（regularization by constraining number of centers and voting weights）。

现在的思路是找出一些“中心”代表（prototypes）。

聚类问题（Clustering Problem）

找代表的过程实际上是一种聚类问题。什么意思呢？

\[\begin{array} { l } \quad \text { if } \mathbf { x } _ { 1 } \approx \mathbf { x } _ { 2 } \\ \Longrightarrow \text { no need both } \operatorname { RBF } \left( \mathbf { x } , \mathbf { x } _ { 1 } \right) \& \operatorname { RBF } \left( \mathbf { x } , \mathbf { x } _ { 2 } \right) \text { in RBFNet } \\ \Longrightarrow \text { cluster } \mathbf { x } _ { 1 } \text { and } \mathbf { x } _ { 2 } \text { by one prototype } \mu \approx \mathbf { x } _ { 1 } \approx \mathbf { x } _ { 2 } \end{array} \]

也就是说 \(\operatorname { RBF } \left( \mathbf { x } , \mathbf { x } _ { 1 } \right)\) 可以很大程度上代表（表示） \(\operatorname { RBF } \left( \mathbf { x } , \mathbf { x } _ { 2 } \right)\)。

那么这种通过代表（代理人）进行聚类（clustering with prototype）的过程为：

1. 将 \(\left\{ \mathbf { x } _ { n } \right\}\) 分为M个互斥（不想交）的集合（disjoint sets）：\(S _ { 1 } , S _ { 2 } , \cdots , S _ { M }\)。
2. 为每一个 \(S_m\) 选择最佳的 \({ \mu } _ { m } \approx \mathbf { x } _ { 1_m } \approx \cdots \approx \mathbf { x } _ { K_m }\) ，其中 \(\mathbf { x } _ { 1_m } \cdots \mathbf { x } _ { K_m } \in S _ { m }\)。

使用平方测量的聚类误差

\[E _ { \mathrm { in } } \left( S _ { 1 } , \cdots , S _ { M } ; \mu _ { 1 } , \cdots , \mu _ { M } \right) = \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \sum _ { m = 1 } ^ { M } \left[ \mathbf { x } _ { n } \in S _ { m } \right] \left\| \mathbf { x } _ { n } - \boldsymbol { \mu } _ { m } \right\| ^ { 2 } \]

所以现在的聚类问题的优化目标为：

\[\min _ { \left\{ S _ { 1 } , \cdots , S _ { M } : \mu _ { 1 } , \cdots , \mu _ { M } \right\} } E _ { i n } \left( S _ { 1 } , \cdots , S _ { M } ; \mu _ { 1 } , \cdots , \mu _ { M } \right) \]

优化（Optimization）

在优化过程中涉及到两个部分的最佳化问题：如何分群以及如何寻找中心点。

这样的组合和数值（ combinatorial-numerical optimization）两个问题结合优化的过程是比较难以优化的：

那么如果只对一个问题寻优，那么问题就会简单很多。

分区寻优（Partition Optimization）

假设 \(\mu _ { 1 } , \mu _ { 2 } , \ldots , \mu _ { k }\) 已经固定，那么一个又一个地通过下面这个公式选择最优的组群：

\[\text { optimal chosen subset } S _ { m } = \text { the one with minimum } \left\| \mathbf { x } _ { n } - \boldsymbol { \mu } _ { m } \right\| ^ { 2 } \]

也就是对于每一个 \(\mathbf { x } _ { n }\) 都在 \(\mu _ { 1 } , \mu _ { 2 } , \ldots , \mu _ { k }\) 中选择最近的 \(\mu _ { m }\) ，并以此为依据进行最优分区（optimally partitioned）。

代表寻优（Prototype Optimization）

假设 \(S _ { 1 } , \cdots , S _ { M }\) 已经固定，那么这个优化问题便成为了一个关于每一个 \(\mu _ m\) 的无约束最优化问题：

\[\nabla _ { \boldsymbol { \mu } _ { m } } E _ { \mathrm { in } } = - 2 \sum _ { n = 1 } ^ { N } \left[ \mathbf { x } _ { n } \in S _ { m } \right] \left[ \mathbf { x } _ { n } - \boldsymbol { \mu } _ { m } \right) = - 2 \left( \left( \sum _ { \mathbf { x } _ { n } \in S _ { m } } \mathbf { x } _ { n } \right) - \left| S _ { m } \right| \boldsymbol { \mu } _ { m } \right) \]

可以看出来最优的代表值便是全部样本的平均值：

\[\text { optimal prototype } \mu _ { m } = \text { average of } \mathbf { x } _ { n } \text { within } S _ { m } \]

对于每个 \(S _ { 1 } , S _ { 2 } , \ldots , S _ { k }\) 都求均值作为最佳 \(\mu_m\) 的计算方法（optimally computed）。

具体实现

\[\begin{array} { l } \text { (1) initialize } \mu _ { 1 } , \mu _ { 2 } , \ldots , \mu _ { k } : \text { say, as } k \text { randomly chosen } x _ { n } \\ \text { (2) alternating optimization of } E _ { \text {in } } \text { : repeatedly } \\ \qquad \text { (1) Optimize } S _ { 1 } , S _ { 2 } , \ldots , S _ { k } : \text { each } x _ { n } \text { optimally partitioned using its closest } \mu _ { i } \\ \qquad \text { (2) Optimize } \mu _ { 1 } , \mu _ { 2 } , \ldots , \mu _ { k } \text { : each } \mu _ { n } \text { optimally computed as the consensus within } S _ { m } \\ \qquad \text { until converge } \end{array} \]

收敛（converge ）：\(S _ { 1 } , S _ { 2 } , \ldots , S _ { k }\) 不再改变。因为上述的交替迭代过程是使得 \(E _ { \text {in } }\) 不断变小的过程，同时\(E _ { \text {in } }\) 的最小值为 0，所以必然收敛。

由于交替寻优（alternating minimization）的特性，K均值算法成为了最流行的距离算法。

正则化RBF网络

使用K均值算法，找出K个具有代表性的 \(\mu _ k\)，来构造 \(N \text{(examples)} \times K \text{(centers)}\) 的 \(\mathrm{Z}\) 矩阵。

那么 RBF Network Using k-Means 的实现过程为：

\[\begin{array} { l } \text { (1) run } k \text { -Means with } k = M \text { to get } \left\{ \boldsymbol { \mu } _ { m } \right\} \\ \text { (2) construct transform } \Phi ( \mathbf { x } ) \text { from RBF (say, Gaussian) at } \mu _ { m } \\ \qquad \mathbf { \Phi } ( \mathbf { x } ) = \left[ \operatorname { RBF } \left( \mathbf { x } , \mu _ { 1 } \right) , \operatorname { RBF } \left( \mathbf { x } , \mu _ { 2 } \right) , \ldots , \operatorname { RBF } \left( \mathbf { x } , \mu _ { M } \right) \right] \\ \text { (3) run linear model on } \left\{ \left( \mathbf { \Phi } \left( \mathbf { x } _ { n } \right) , y _ { n } \right) \right\} \text { to get } \beta \\ \text { (4) return } g _ { \text {RBFNET } } ( \mathbf { x } ) = \text { LinearHypothesis } ( \boldsymbol { \beta } , \mathbf { \Phi } ( \mathbf { x } ) ) \end{array} \]

这实际上就是使用无监督学习方法来辅助特征转换（using unsupervised learning (k-Means) to assist feature transform）。需要的参数有两个：一个是代表的个数 \(M\)，另一个是RBF的选择（比如中心为 \(\gamma\) 的高斯函数）。

k-Means和RBF网络的实际应用（k-Means and RBF Network in Action）

K-Means in Action

下面展示k-Means算法的实际优化过程：

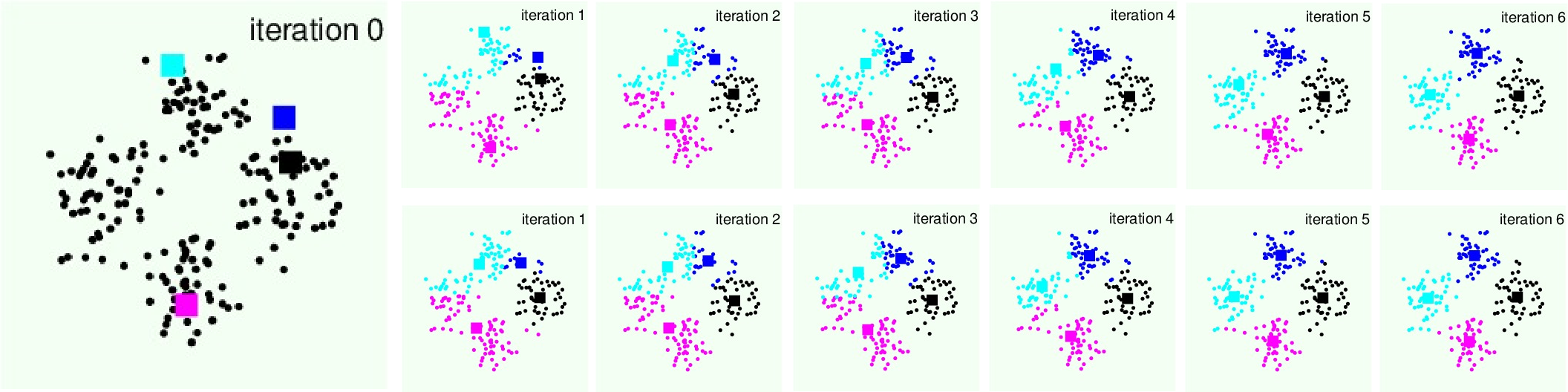
其中第一行是分区优化，第二行是代表（中心点）寻优。可看出合理的初始值和k可以获得不错的聚类效果。

RBF Network Using k-Means in Action

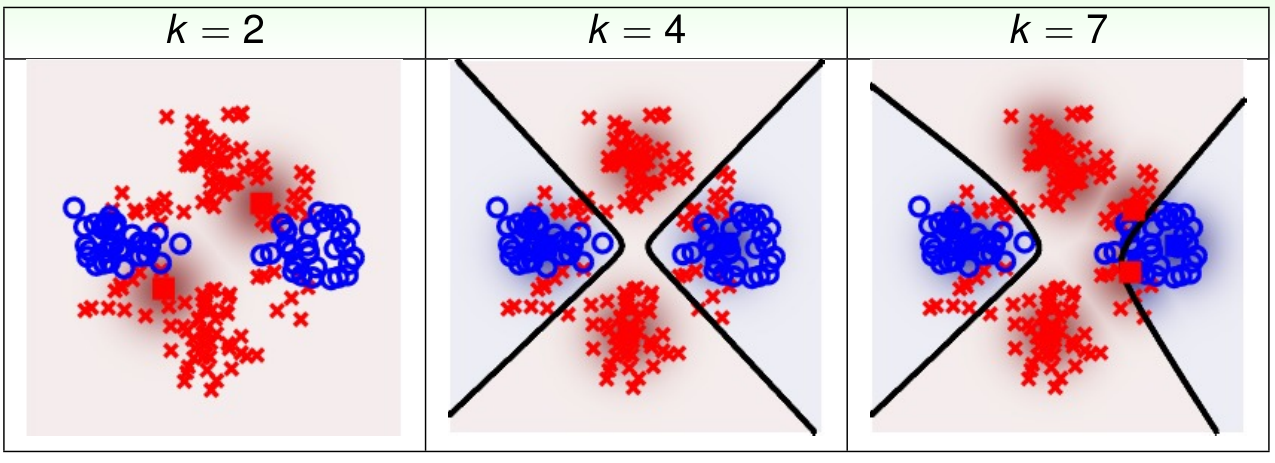
图中发黑的地方代表了高斯密度函数的分布形式。可以看出合理的中心点可以使得 RBF Network 获得比较好的效果。

Full RBF Network in Action

最左边是使用了正则化的RBF的分类效果。最右边是最近邻算法的分类效果。因为两者在一定程度上都用到了全部的数据，所以看起来有些过拟合。所以在实际运用中完全 RBF 网络很少使用。