核逻辑回归(Kernel Logistic Regression)
SVM 和 Regularization 之间的联系
软间隔支持向量机的原最优化问题为:
\[\begin{aligned} \min _ { b , \mathbf { w } , \xi } & \frac { 1 } { 2 } \mathbf { w } ^ { T } \mathbf { w } + C \cdot \sum _ { n = 1 } ^ { N } \xi _ { n } \\ \text { s.t. } & y _ { n } \left( \mathbf { w } ^ { T } \mathbf { z } _ { n } + b \right) \geq 1 - \xi _ { n } \text { and } \xi _ { n } \geq 0 \text { for all } n \end{aligned}
\]
转换为无约束问题如下:
\[\min _ { b , \mathbf { w } } \quad \frac { 1 } { 2 } \mathbf { w } ^ { T } \mathbf { w } + C \underbrace{\sum _ { n = 1 } ^ { N } \max \left( 1 - y _ { n } \left( \mathbf { w } ^ { T } \mathbf { z } _ { n } + b \right) , 0 \right)}_{\widehat { \mathrm { err } }}
\]
可简化为:
\[\min \quad \frac { 1 } { 2 } \mathbf { w } ^ { \top } \mathbf { w } + C \sum \widehat { \mathrm { err } }
\]
与 L2 范数正则化相比:
\[\min \quad \frac { \lambda } { N } \mathbf { w } ^ { T } \mathbf { w } + \frac { 1 } { N } \sum \mathrm { err }
\]
可见两者十分相似。但是为什么不用该无约束问题求解呢:这是因为:
- 这不是一个 QP 问题,不能使用核技巧
- 取最大函数不是可微的,很难求解。
下面列出 SVM 与其他模型的简单对比:
\[\begin{array} { c | c | c } & \text { minimize } & \text { constraint } \\ \hline \text { regularization by constraint } & E _ { \text {in } } & \mathbf { w } ^ { T } \mathbf { w } \leq C \\ \hline \text { hard-margin SVM } & \mathbf { w } ^ { T } \mathbf { w } & E _ { \text {in } } = 0 \text { [and more] } \\ \hline \hline \text { L2 regularization } & \frac { \lambda } { N } \mathbf { w } ^ { T } \mathbf { w } + E _ { \text {in } } & \\ \hline \text { soft-margin SVM } & \frac { 1 } { 2 } \mathbf { w } ^ { T } \mathbf { w } + C N \widehat {E _ { \text {in } }} & \\ \end{array}
\]
可以观察出以下特性:
\[\begin{array} { c } \text { large margin } \Longleftrightarrow \text { fewer hyperplanes } \Longleftrightarrow L 2 \text { regularization of short w } \\ \text { soft margin } \Longleftrightarrow \text { special } \widehat { \text { err } } \\ \text { larger } C \Longleftrightarrow \text { smaller } \lambda \Longleftrightarrow \text { less regularization } \end{array}
\]
即间隔越大意味着更少的超平面,类似于L2正则化中系数的衰减。\(C\) 越大意味着更小的 \(\lambda\),更弱的正则化。
将SVM看作一种正则化方法的话,可以跟简单理解如何扩展和连接到其他学习模型。
SVM 和 Logistic Regression 之间的联系
现在令 \(\text { linear score } s = \mathbf { w } ^ { T } \mathbf { z } _ { n } + b\),那么不同的误差测量(Error Measure)表达式可以写为:
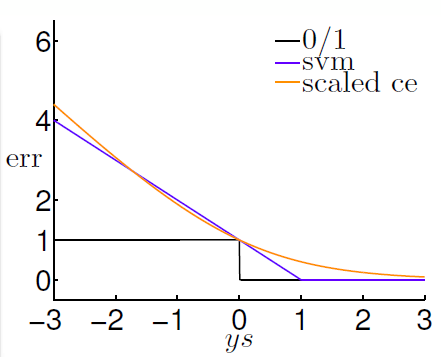
\[\begin{array} { l } \operatorname { err } _ { 0 / 1 } ( s , y ) = [ y s \leq 0 ] \\ \operatorname { err } _ { \text {svm } } ( s , y ) = \max ( 1 - y s , 0 ) \\\operatorname { err } _ { \text {sce } }( s , y ) = \log _ { 2 } ( 1 + \exp ( - y s ) ) \text { : } \end{array}
\]
其中 \(\operatorname { err } _ { \text {svm} }\) 和 \(\operatorname { err } _ { \text {sce} }\) 均是 \(\operatorname{ err } _ { 0 / 1 }\) 的凸上限,\(\operatorname { err } _ { \text {sce} }\) 用在 Logistic Regression 中做误差测量。
具体如下图所示:
![在这里插入图片描述]()
\[\begin{array} { ccccc } - \infty & \longleftarrow & y s & \longrightarrow & & + \infty \\ \approx - y s & & \widehat { \mathrm { err } } _ { \mathrm { svm } } ( S , y ) & && = 0 \\ \approx - y s & & ( \ln 2 ) \cdot \operatorname { err }_{\text{sce}} ( s , y ) & & & \approx 0 \end{array}
\]
所以可以看出 regularized LogReg 与 SVM 十分相似。
两阶段学习模型(Two-Level-Learning)
如何实现呢?概括来说为使用逻辑回归在经过SVM映射的空间上学习。所以叫两阶段学习模型(Two-Level-Learning)。具体步骤为:
- 使用 SVM 找出分割超平面
- 在超平面周围,根据距离,使用 Logistic Regression 学习出真实分数。具体操作为通过缩放(A 和 \(\theta\))和 偏移(B)建立距离和分数之间的联系。
数学表达如下:
\[g ( \mathbf { x } ) = \theta \left( A \cdot \left( \mathbf { w} _ { \mathrm { svm } } ^ { T } \mathbf { \Phi } ( \mathbf { x } ) + b _ { \mathrm { SVM } } \right) + B \right)
\]
通常 \(A > 0, B \approx 0\) 更合理一些。\(A > 0\) 代表了SVM的分类结果大体是对的,\(B \approx 0\) 代表了分割超平面与实际值偏差很小。
可以写出其显示数学表达:
\[\min _ { A , B } \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \log \left( 1 + \exp \left( - y _ { n } ( A \cdot ( \underbrace { \mathbf { w } _ { \mathrm { SVM } } ^ { T } \mathbf { \Phi } \left( \mathbf { x } _ { n } \right) + b _ { \mathrm { SVM } } } _ { \Phi _ { \mathrm { SVM } } \left( \mathbf { x } _ { n } \right) } ) + B ) \right) \right)
\]
那么该两阶段学习模型的具体步骤为:
\[\begin{array} { l } 1. \text { run SVM on } \mathcal { D } \text { to get } \left( b _ { \mathrm { svm} } , \mathbf { w } _ { \mathrm { svm} } \right) [ \mathrm { or } \text { the equivalent } \alpha ] , \text { and } \text { transform } \mathcal { D } \text { to } \mathbf { z } _ { n } ^ { \prime } = \mathbf { w } _ { \mathrm { SVM } } ^ { T } \mathbf { \Phi } \left( \mathbf { X } _ { n } \right) + b _ { \mathrm { SVM } } \\ \text { -actulal model performs this step in a more complicated manner } \\ 2. \text { run LogReg on } \left\{ \left( \mathbf { z } _ { n } ^ { \prime } , y _ { n } \right) \right\} _ { n = 1 } ^ { N } \text { to get } ( A , B ) \\ \text { -actual model adds some special regularization here } \\ 3. \text { return } g ( \mathbf { x } ) = \theta \left( A \cdot \left( \mathbf { w } _ { \mathrm { svm} } ^ { T } \mathbf { \Phi } ( \mathbf { x } ) + b _ { \mathrm { svm} } \right) + B \right) \end{array}
\]
核逻辑回归(Kernel Logistic Regression)
前面提到的二阶段学习模型是一种核逻辑回归的近似解法,那么如何实现真正的核逻辑回归呢?
关键是最优解 \(\mathbf { w } _ { * }\) 满足一下条件:
\[\mathbf { w } _ { * } = \sum _ { n = 1 } ^ { N } \beta _ { n } \mathbf { z } _ { n }
\]
因为 \(\mathbf { w } _ { * } ^ { T } \mathbf { z } = \sum _ { n = 1 } ^ { N } \beta _ { n } \mathbf { z } _ { n } ^ { T } \mathbf { z } = \sum _ { n = 1 } ^ { N } \beta _ { n } K \left( \mathbf { x } _ { n } , \mathbf { x } \right)\),这样的话便可以使用核技巧了。
那么对于任何一个L2正则化线性模型(L2-regularized linear model)即:
\[\min _ { \mathbf { w } } \frac { \lambda } { N } \mathbf { w } ^ { T } \mathbf { w } + \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \operatorname { err } \left( y _ { n } , \mathbf { w } ^ { T } \mathbf { z } _ { n } \right)
\]
现在假设其最优解由两个部分组成,\(\mathbf { w } _ { \| } \in \operatorname { span } \left( \mathbf { z } _ { n } \right)\) 及 \(\mathbf { w } _ { \perp } \perp \operatorname { span } \left( \mathbf { z } _ { n } \right)\) 即:
\[\mathbf { w } _ { * } = \mathbf { w } _ { \| } + \mathbf { w } _ { \perp }
\]
那么有:
\[\mathbf { w } _ { * } ^ { T } \mathbf { w } _ { * } = \mathbf { w } _ { \| } ^ { T } \mathbf { w } _ { \| } + 2 \mathbf { w } _ { \| } ^ { T } \mathbf { w } _ { \perp } + \mathbf { w } _ { \perp } ^ { T } \mathbf { w } _ { \perp } \quad > \mathbf { w } _ { \| } ^ { T } \mathbf { w } _ { \| }
\]
也就是说 \(\mathbf { w } _ { \| }\) 优于 \(\mathbf { w } _ { * }\),与 \(\mathbf { w } _ { * }\) 是最优解的假设相悖,所以 \(\mathbf { w } _ { * } = \mathbf { w } _ { \| }\),不存在 \(\mathbf { w } _ { \perp }\)。也就是说 \(\mathbf { w } _ { * }\) 可以由 \(\mathbf{z}_n\) 组成,\(\mathbf { w } _ { * }\) 位于 \(\mathcal{Z}\) 空间。
所以说任何一个L2正则化线性模型都可以被kernel,所以可以改写为:
\[\min _ { \beta } \frac { \lambda } { N } \sum _ { n = 1 } ^ { N } \sum _ { m = 1 } ^ { N } \beta _ { n } \beta _ { m } K \left( \mathbf { x } _ { n } , \mathbf { x } _ { m } \right) + \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \log \left( 1 + \exp \left( - y _ { n } \sum _ { m = 1 } ^ { N } \beta _ { m } K \left( \mathbf { x } _ { m } , \mathbf { x } _ { n } \right) \right) \right)
\]
至此便可以使用 GD/SGD 等优化算法进行寻优了。值得注意的是虽然与SVM相似,但是与SVM不同的是其系数 \(\beta_n\) 常常是非零的。
核岭回归(Kernel Ridge Regression)
岭回归的原问题模型如下:
\[\min _ { \mathbf { w } } \frac { \lambda } { N } \mathbf { w } ^ { T } \mathbf { w } + \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \left( y _ { n } - \mathbf { w } ^ { T } \mathbf { z } _ { n } \right) ^ { 2 }
\]
前文已经证得任何L2正则化线性模型都可以被 kernel,所以这里写出核岭回归的数学表达为:
\[\begin{aligned} \min _ { \boldsymbol { \beta } } & \underbrace{\frac { \lambda } { N } \sum _ { n = 1 } ^ { N } \sum _ { m = 1 } ^ { N } \beta _ { n } \beta _ { m } K \left( \mathbf { x } _ { n } , \mathbf { x } _ { m } \right)}_{ \text {regularization of } \beta \text{ K-based features } } + \frac { 1 } { N } \underbrace { \sum _ { n = 1 } ^ { N } \left( y _ { n } - \sum _ { m = 1 } ^ { N } \beta _ { m } K \left( \mathbf { x } _ { n } , \mathbf { x } _ { m } \right) \right) ^ { 2 } } _ { \text {linear regression of } \beta \text{ K-based features } \boldsymbol { \beta } }\\ & = \frac { \lambda } { N } \boldsymbol { \beta } ^ { T } \mathbf { K } \boldsymbol { \beta } + \frac { 1 } { N } \left( \boldsymbol { \beta } ^ { T } \mathbf { K } ^ { T } \mathbf { K } \boldsymbol { \beta } - 2 \boldsymbol { \beta } ^ { T } \mathbf { K } ^ { T } \mathbf { y } + \mathbf { y } ^ { T } \mathbf { y } \right) \end{aligned}
\]
也就是说之前得所有核技巧都可以用到这里。
那么可以根据目标函数导数为零,求出系数 \(\beta\) 的解析解,其目标函数的导数求得如下:
\[\nabla E _ { \mathrm { aug } } ( \beta ) = \frac { 2 } { N } \left( \lambda \mathrm { K } ^ { T } \mathrm { I } \beta + \mathrm { K } ^ { T } \mathrm { K } \beta - \mathrm { K } ^ { T } \mathbf { y } \right) = \frac { 2 } { N } \mathrm { K } ^ { T } ( ( \lambda \mathrm { I } + \mathrm { K } ) \beta - \mathrm { y } )
\]
令其为零有:
\[\beta = ( \lambda I + K ) ^ { - 1 } y
\]
由于 \(K\) 必然是半正定的(根据 Mercer’s condition),那么当 \(\lambda > 0\) 时,\(( \lambda I + K ) ^ { - 1 }\) 必然存在。这里的稠密矩阵求逆操作的时间复杂度为:\(O(N^3)\)。值得注意的是虽然与SVM相似,但是与SVM不同的是其系数 \(\beta_n\) 常常是非零的。
支持向量回归(Support Vector Regression)
管回归(Tube Regression)
管回归说的是在回归线周围一定范围内,不算错误,即实际值和预测值的差在一定范围内认为其无错:
\[\begin{array} { l } | s - y | \leq \epsilon : 0 \\ | s - y | > \epsilon : | s - y | - \epsilon \end{array}
\]
即
\[\operatorname { err } ( y , s ) = \max ( 0 , | s - y | - \epsilon ) \\
\]
该误差叫做 \(\epsilon\)-insensitive error(不敏感误差)。
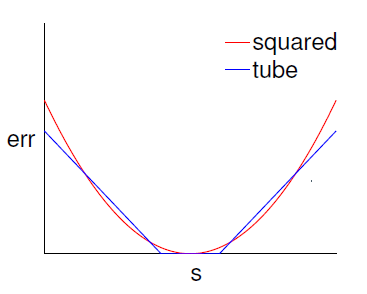
与平方(squared)误差 \(\operatorname { err } ( y , s ) = ( s - y ) ^ { 2 }\) 相比,当 \(| s - y |\) 较小时,两者相似。但是当 \(| s - y |\) 较大时,增长较缓,也就是杂讯(nosie)的影响相较小。
![在这里插入图片描述]()
那么 L2 管回归 的优化目标为:
\[\min _ { \mathbf { w } } \frac { \lambda } { N } \mathbf { w } ^ { T } \mathbf { w } + \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \max \left( 0 , \left| \mathbf { w } ^ { T } \mathbf { z } _ { n } - y \right| - \epsilon \right)
\]
标准支持向量回归(Standard Support Vector Regression)
为了使用 SVM 的优点(稀疏系数矩阵),现在将 L2 管回归的系数改变一下:
\[\min _ { b , \mathbf { w } } \quad \frac { 1 } { 2 } \mathbf { w } ^ { T } \mathbf { w } + C \sum _ { n = 1 } ^ { N } \max \left( 0 , \left| \mathbf { w } ^ { T } \mathbf { z } _ { n } + b - y _ { n } \right| - \epsilon \right)
\]
同时由于这里的max操作不可微,所以需要转换一下:
\[\begin{aligned} \min _ { b , \mathbf { w } , \xi ^ { \vee } , \xi ^ { \wedge } } & \frac { 1 } { 2 } \mathbf { w } ^ { T } \mathbf { w } + C \sum _ { n = 1 } ^ { N } \left( \xi _ { n } ^ { \vee } + \xi _ { n } ^ { \wedge } \right) \\ \text { s.t. } & - \epsilon - \xi _ { n } ^ { \vee } \leq y _ { n } - \mathbf { w } ^ { T } \mathbf { z } _ { n } - b \leq \epsilon + \xi _ { n } ^ { \wedge } \\ & \xi _ { n } ^ { \vee } \geq 0 , \xi _ { n } ^ { \wedge } \geq 0 \end{aligned}
\]
由于这里有上下两个边界,所以相比SVM多了一个辅助系数,需要 \(\xi _ { n } ^ { \vee } , \xi _ { n } ^ { \wedge }\) 两个辅助系数。至此便可以使用二次规划求解最优值了。
对偶支持向量回归(Dual Support Vector Regression)
为了使用核技巧,仍需求解对偶问题。这里引入两个拉格朗日乘数 \(\alpha_ { n } ^ { \vee } , \alpha_ { n } ^ { \wedge }\)
\[\begin{array} { l l l } \text { objective function } & &\frac { 1 } { 2 } \mathbf { w } ^ { T } \mathbf { w } + C \sum _ { n = 1 } ^ { N } \left( \xi _ { n } ^ { \vee } + \xi _ { n } ^ { \wedge } \right) \\ \text { Lagrange multiplier } \alpha _ { n } ^ { \wedge } & \text { for } & y _ { n } - \mathbf { w } ^ { T } \mathbf { z } _ { n } - b \leq \epsilon + \xi _ { n } ^ { \wedge } \\ \text { Lagrange multiplier } \alpha _ { n } ^ { \vee } & \text { for } & - \epsilon - \xi _ { n } ^ { \vee } \leq y _ { n } - \mathbf { w } ^ { T } \mathbf { z } _ { n } - b \end{array}
\]
某些 KKT 条件如下:
\[\begin{array} { l }
\frac { \partial \mathcal { L } } { \partial w _ { i } } = 0 : \mathbf { w } = \sum _ { n = 1 } ^ { N } \underbrace { \left( \alpha _ { n } ^ { \wedge } - \alpha _ { n } ^ { \vee } \right) } _ { \beta_n } \mathbf { z } _ { n } \\ \frac { \partial \mathcal { L } } { \partial b } = 0 : \sum _ { n = 1 } ^ { N } \left( \alpha _ { n } ^ { \wedge } - \alpha _ { n } ^ { \vee } \right) = 0 \\
\alpha _ { n } ^ { \wedge } \left( \epsilon + \xi _ { n } ^ { \wedge } - y _ { n } + \mathbf { w } ^ { T } \mathbf { z } _ { n } + b \right) = 0 \\ \alpha _ { n } ^ { \vee } \left( \epsilon + \xi _ { n } ^ { \vee } + y _ { n } - \mathbf { w } ^ { T } \mathbf { z } _ { n } - b \right) = 0 \end{array}
\]
与SVM求解过程类似,可以写出其对偶问题如下:
\[\begin{aligned} \min & \frac { 1 } { 2 } \sum _ { n = 1 } ^ { N } \sum _ { m = 1 } ^ { N } \left( \alpha _ { n } ^ { \wedge } - \alpha _ { n } ^ { \vee } \right) \left( \alpha _ { m } ^ { \wedge } - \alpha _ { m } ^ { \vee } \right) k _ { n , m } \\ & + \sum _ { n = 1 } ^ { N } \left( \left( \epsilon - y _ { n } \right) \cdot \alpha _ { n } ^ { \wedge } + \left( \epsilon + y _ { n } \right) \cdot \alpha _ { n } ^ { \vee } \right) \\ \text { s.t. } & \sum _ { n = 1 } ^ { N } \left( \alpha _ { n } ^ { \wedge } - \alpha _ { n } ^ { \vee } \right) = 0 \\ & 0 \leq \alpha _ { n } ^ { \wedge } \leq C , 0 \leq \alpha _ { n } ^ { \vee } \leq C \end{aligned}
\]
系数的稀疏性分析:
当 \(\left| \mathbf { w } ^ { T } \mathbf { z } _ { n } + b - y _ { n } \right| < \epsilon\) ,也就是说样本严格位于管内,那么会有:
\[\begin{array} { l } \Longrightarrow \xi _ { n } ^ { \wedge } = 0 \text { and } \xi _ { n } ^ { \vee } = 0 \\ \Longrightarrow \left( \epsilon + \xi _ { n } ^ { \wedge } - y _ { n } + \mathbf { w } ^ { T } \mathbf { z } _ { n } + b \right) \neq 0 \text { and } \left( \epsilon + \xi _ { n } ^ { \vee } + y _ { n } - \mathbf { w } ^ { T } \mathbf { z } _ { n } - b \right) \neq 0 \\ \Longrightarrow \alpha _ { n } ^ { \wedge } = 0 \text { and } \alpha _ { n } ^ { \vee } = 0 \\ \Longrightarrow \beta _ { n } = 0 \end{array}
\]
所以说 \(\beta\) 是稀疏的,同时在 SVR 中,哪些在管上或外的样本(\(\beta_n \neq 0\))叫做支持向量。
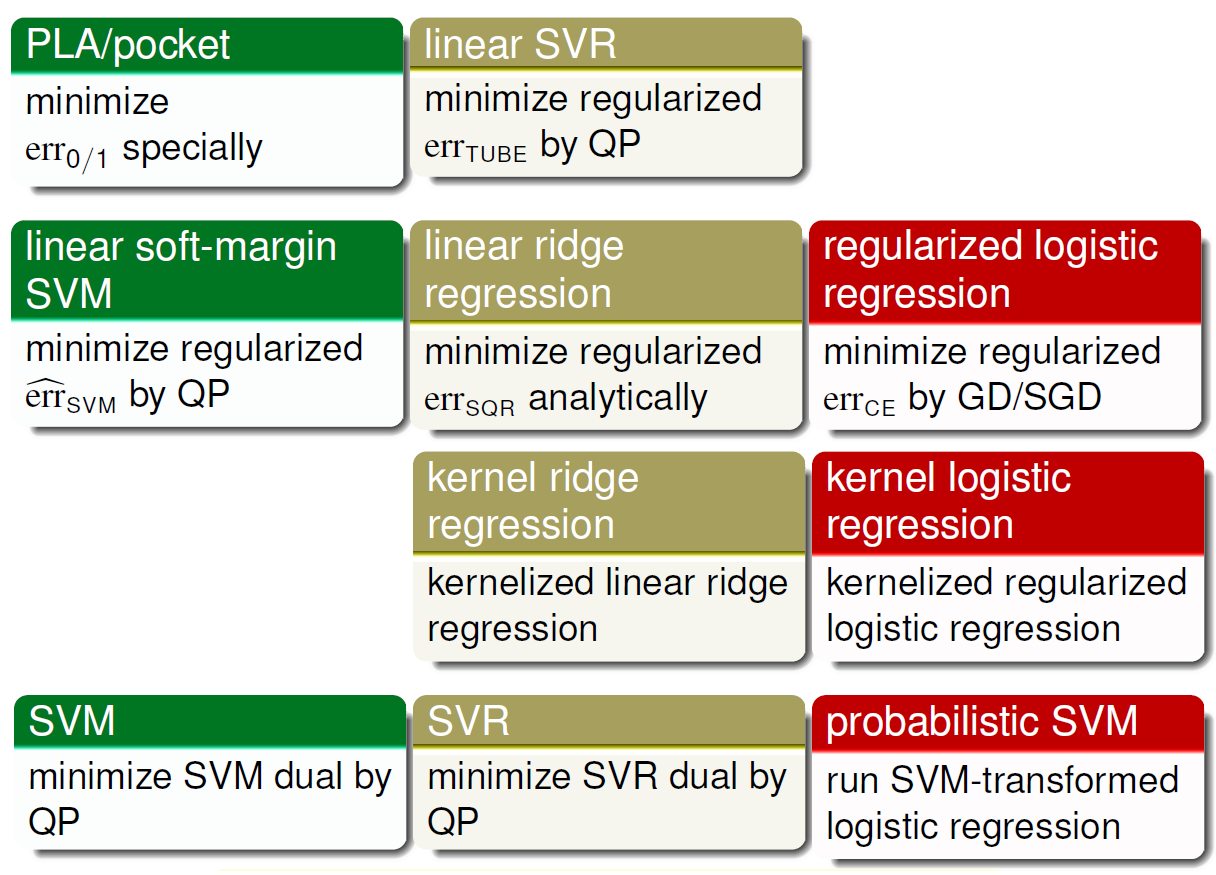
线性或核模型总结
![在这里插入图片描述]()
- 第一行由于效果不好,所以不太常用。
- 第二行比较常用的工具箱是LIBLINEAR
- 第三行由于其稠密的 \(\beta\) 所以也不太常用
- 第四行比较常用的工具箱是LIBSVM



 浙公网安备 33010602011771号
浙公网安备 33010602011771号