主成分分析（Principal Components Analysis）

主成分分析PCA(Principal Component Analysis),作用是:

1. 聚类 Clustering：把复杂的多维数据点,简化成少量数据点,易于分簇
2. 降维：降低高维数据,简化计算,达到数据降维,压缩,降噪的目的

PCA 的目的就是找到一个低维映射空间，使得数据映射后方差最大。

理论实现：

首先对样本空间为 \(d\) 维全部的数据中心化，使得均值为 0，即将所有的样本与样本均值相减获得新的样本：

\[\mathbf { x } _ { i } = \mathbf { x } _ { i } - \mu \]

也就是说转换后：

\[\frac { 1 } { N } \sum _ { i = 1 } ^ { N } \mathbf { x } _ { i } = 0_d \]

知识补充：

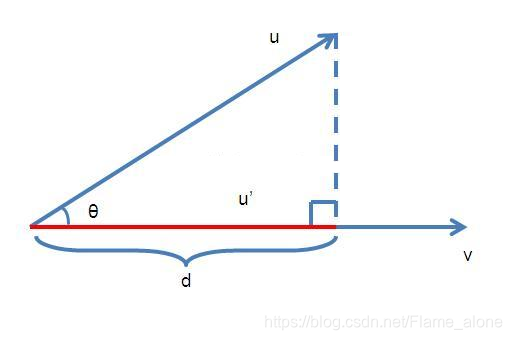
求向量 u 在向量 v 上的投影：

那么根据上图可以列出以下公式

\[\begin{aligned} u ^ { \prime } & = \frac { d } { | v | } v \\ d & = | u | \cos \theta \\ \cos \theta & = \frac { u^T \cdot v } { | u | | v | } \end{aligned} \]

所以可以解出向量 \(u\) 在向量 \(v\) 上的投影 \(u^\prime\) 为：

\[u^\prime = \frac { u ^ T \cdot v } { | v | ^ { 2 } } v \]

那么将向量 \(v\) 所在直线视为一维空间，那么向量 \(u\) 映射在该维度的表示为

\[u^v = \frac { u ^ T \cdot v } { | v | } = \frac { v ^ T \cdot u } { | v | } \]

也就是说映射后的长度（有方向）成为向量 \(u\) 映射在该维度的表示。

那么现在求取映射后空间，先考虑映射到一维空间，也就是说向一个向量做投影，假如现在向向量 \(u _ { 1 }\) 做投影。

那么由于一开始的中心化操作，使得映射后均值仍然为零：

\[\frac { 1 } { n } \sum _ { i = 1 } ^ { n } \frac { u _ { 1 } ^ { T } } { | u _ { 1 } | } \mathbf x _ { i } = \frac { u _ { 1 } ^ { T } } { | u _ { 1 } | } \sum _ { i = 1 } ^ { n } \frac { 1 } { n } \mathbf x _ { i } = 0 \]

那么映射后的方差有：

\[ \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \left( \frac { u _ { 1 } ^ { T } } { | u _ { 1 } | } \mathbf x _ { i } - 0\right) ^ { 2 } = \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \frac { u _ { 1 } ^ { T } } { | u _ { 1 } | } \mathbf x _ { i } \mathbf x _ { i } ^ { T } \frac { u _ { 1 } } { | u _ { 1 } | } = \frac { u _ { 1 } ^ { T } } { | u _ { 1 } | } \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \mathbf x _ { i } \mathbf x _ { i } ^ { T } \frac { u _ { 1 } } { | u _ { 1 } | } =\frac { u _ { 1 } ^ { T } } { | u _ { 1 } | }S \frac { u _ { 1 } } { | u _ { 1 } | } \]

其中 \(S\) 为数据集的协方差矩阵：

\[S = \frac { 1 } { n } \sum _ { i , j = 1 } ^ { n } \mathbf x _ { i } ^ { T } \cdot \mathbf x _ { j } \]

现在想要映射在该一维空间后数据的方差最大，那么该优化问题为：

\[\begin{aligned} \max _ { u _ { 1 } } \quad & u _ { 1 } ^ { T } \cdot S \cdot u _ { 1 } \\ \text { s.t.} \quad & \left\| u _ { 1 } \right\| _ { 2 } ^ { 2 } = 1 \end{aligned} \]

其中为了方便，将映射向量的长度定为一作为约束条件。为了去掉这一约束条件，使用拉格朗日乘数法转换该最优化问题：

\[ \max _ { u _ { 1 } } \left\{ u _ { 1 } ^ { T } \cdot S \cdot u _ { 1 } + \lambda \left( 1 - \left\| u _ { 1 } \right\| _ { 2 } ^ { 2 } \right) \right\} \]

对于凸优化问题，在最优点出导数为零，所以最优解的必要条件为：

\[2 u _ { 1 } \cdot S + \lambda \left( - 2 u _ { 1 } \right) = 0 \]

也就是说：

\[S u _ { 1 } = \lambda u _ { 1 } \]

可以看出 \(u _ { 1 }\) 是协方差矩阵 \(S\) 的一个特征向量，那么现在代入到原最优化问题：

\[\begin{aligned} \max _ { u _ { 1 } } \quad & u _ { 1 } ^ { T } \cdot \lambda \cdot u _ { 1 } \\ \text { s.t.} \quad & \left\| u _ { 1 } \right\| _ { 2 } ^ { 2 } = 1 \end{aligned} \]

可以进一步转换为：

\[\begin{aligned} \max _ { u _ { 1 } } \quad & \lambda \\ \text { s.t.} \quad & \left\| u _ { 1 } \right\| _ { 2 } ^ { 2 } = 1 \end{aligned} \]

也就是说在约束条件下希望该特征值最大。那么推广到多维空间映射，仍然适用。那么最佳的多维空间则由 Top \(d^{\prime}\) 特征值（最大的\(d^{\prime}\) 个特征值）所对应的特征向量构成。

那么PCA的具体实现流程 ：

\[\begin{aligned} & \text { 1. let }\overline { \mathbf { x } } = \frac { 1 } { N } \sum _ { n = 1 } ^ { N } \mathbf { x } _ { n } , \text { and let } \mathbf { x } _ { n } \leftarrow \mathbf { x } _ { n } - \overline { \mathbf { x } } , X^T = [\mathbf x_1,\cdots,\mathbf x_N] \\ & \text { 2. calculate } \tilde { d } \text { top eigenvectors } \mathbf { w } _ { 1 } , \mathbf { w } _ { 2 } , \ldots , \mathbf { w } _ { \tilde { d } } \text { of } \mathbf { X } ^ { T } \mathbf { X } \\ & \text { 3. return feature transform } \mathbf { \Phi } ( \mathbf { x } ) = \mathbf { W } ( \mathbf { x } - \overline { \mathbf { x } } ) \end{aligned} \]