假如现在有 \(\ell\) 个同一分布的观察数据,每条数据都有 \(p\) 个特征。如果现在加入一个或多个观察数据,那么是否这些数据与原有的数据十分不同,甚至我们可以怀疑其是否属于同一分布呢?反过来讲,是否这些数据与原有的数据十分相似,我们无法将其区分呢?这便是异常检测工具和方法需要解决的问题。即现在只有正常的数据,那么当异常数据加入时,我们是否可以将其分辨出来呢?
通常情况下,要学习训练出一个在 \(p\) 维空间上的粗糙封闭的边界线,来分割出初始观测分布的轮廓线。然后,如果观测数据位于边界限定的子空间内,则认为它们来自与初始观测相同的总体。否则,如果他们在边界之外,我们可以在一定程度上说他们是异常的。
OCSVM
一种实现方法是 One-Class SVM (OCSVM),首次是在论文《Support Vector Method for Novelty Detection》中由 Bernhard Schölkopf 等人在 2000 年提出, 其与 SVM 的原理类似,更像是将零点作为负样本点,其他数据作为正样本点,来训练支持向量机。策略是将数据映射到与内核相对应的特征空间,在数据与原点间构建超平面,该超平面与原点呈最大距离。
现在假设该超平面为:
\[w \cdot \Phi ( \mathbf { x } ) - \rho = 0
\]
目标就是在分类正确的基础上最大化超平面与原点的距离:
\[\begin{array} { c c } \mathop{ \max} \limits_ { w \in F , \rho \in \mathbb { R } } & { |\rho| } / { \| w \| ^ { 2 }} \\ \text { subject to } & \left( w \cdot \Phi \left( \mathbf { x } _ { i } \right) \right) \geq \rho \end{array}
\]
同时根据超平面的定义,实际上 \(\rho\) 的正负和 \(w\) 向量中的元素正负同时调整就不会影响超平面,那么假如 \(\rho > 0\) ,那么优化问题可以重写为:
\[\mathop{ \max} \limits_ { w \in F , \rho \in \mathbb { R } } { \rho} / { \| w \| ^ { 2 }}
\]
为了防止参数求解的耦合问题,可以将其拆解为
\[\begin{aligned}
\mathop{ \max} \limits_ { w \in F , \rho \in \mathbb { R } } { \rho} + 1/{ \| w \| ^ { 2 }} \\
\mathop{ \min} \limits_ { w \in F , \rho \in \mathbb { R } } - { \rho} + { \| w \| ^ { 2 }}
\end{aligned}
\]
这样的话在求解问题时,由于 \(w\) 向量中元素的整体正负不会影响 \({ \| w \| ^ { 2 }}\) 的取值,那么其会保证 \(\rho\) 的最终取值为正值,也就是满足假设。同时为了方便梯度求解,将 \({ \| w \| ^ { 2 }}\) 添加一个 \(\frac{1}{2}\) 那么最终的优化目标可以写为:
\[\begin{array} { c c } \mathop{ \min} \limits_ { w \in F , \rho \in \mathbb { R } } & - { \rho} + \frac{1}{2}{ \| w \| ^ { 2 }} \\ \text { subject to } & \left( w \cdot \Phi \left( \mathbf { x } _ { i } \right) \right) \geq \rho \end{array}
\]
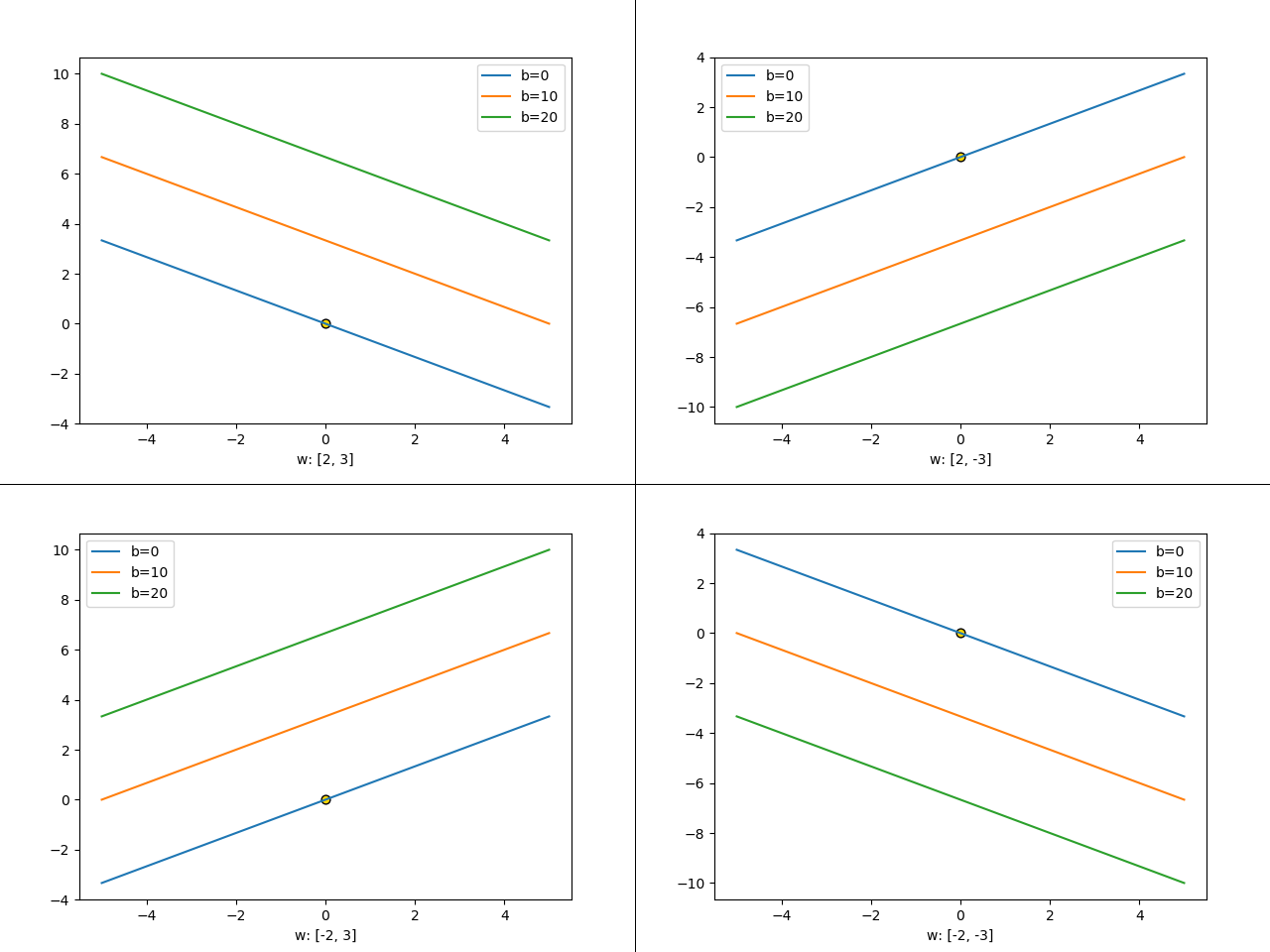
从另一方面想,实际上对于一个斜率一定的直线,当其偏移量的绝对值越大时,其离零点越来越近,下面以 \(w * x - b = 0\) 为例,当 w 确定时,\(|b|\) 越大,直线离原点越远:
![在这里插入图片描述]()
加入松弛变量 \(\xi\) 后,其优化的目标函数可以写为:
\[\begin{array} { c c } \mathop{ \min} \limits_ { w \in F , \boldsymbol { \xi } \in \mathbb { R } ^ { \ell } , \rho \in \mathbb { R } } & \frac { 1 } { 2 } \| w \| ^ { 2 } + \frac { 1 } { \nu \ell } \sum _ { i } \xi _ { i } - \rho \\ \text { subject to } & \left( w \cdot \Phi \left( \mathbf { x } _ { i } \right) \right) \geq \rho - \xi _ { i } , \quad \xi _ { i } \geq 0 \end{array}
\]
其中 \(v \in (0,1)\) 用于调节松弛程度,根据该目标函数进行优化求解得到 \(w\) 和 \(\rho\) 后,对多部分样本来说,其决策函数 \(f ( \mathbf { x } ) = \operatorname { sgn } ( ( w \cdot \Phi ( \mathbf { x } ) ) - \rho )\) 输出为正。
为了求解对偶问题使用核技巧,这里使用 Lagrange 乘数 \(\alpha_i,\beta_i\),可以写出拉格朗日方程:
\[\begin{aligned} L ( w , \boldsymbol { \xi } , \rho , \boldsymbol { \alpha } , \boldsymbol { \beta } ) = & \frac { 1 } { 2 } \| w \| ^ { 2 } + \frac { 1 } { v \ell } \sum _ { i } \xi _ { i } - \rho \\ & - \sum _ { i } \alpha _ { i } \left( \left( w \cdot \Phi \left( \mathbf { x } _ { i } \right) \right) - \rho + \xi _ { i } \right) - \sum _ { i } \boldsymbol { \beta } _ { i } \xi _ { i } \end{aligned}
\]
那么根据对参数 \(w , { \xi } , \rho\) 求偏导,可以写出部分 KKT条件:
\[\begin{aligned} w & = \sum _ { i } \alpha _ { i } \Phi \left( \mathbf { x } _ { i } \right) \\ \alpha _ { i } & = \frac { 1 } { v \ell } - \boldsymbol { \beta } _ { i } \leq \frac { 1 } { v \ell } , \quad \sum _ { i } \alpha _ { i } = 1 \end{aligned}
\]
那么通过导出对偶问题和使用核技巧,便可以实现通过支持向量 \(\left\{ \mathbf { x } _ { i } : i \in [ \ell ] , \alpha _ { i } > 0 \right\}\) 求得决策函数:
\[f ( \mathbf { x } ) = \operatorname { sgn } \left( \sum _ { i } \alpha _ { i } k \left( \mathbf { x } _ { i } , \mathbf { x } \right) - \rho \right)
\]
现在也可以写出对偶问题了:
\[\min _ { \boldsymbol { \alpha } } \frac { 1 } { 2 } \sum _ { i j } \alpha _ { i } \alpha _ { j } k \left( \mathbf { x } _ { i } , \mathbf { x } _ { j } \right) \text { subject to } 0 \leq \alpha _ { i } \leq \frac { 1 } { \nu \ell } , \sum _ { i } \alpha _ { i } = 1
\]
之后使用二次规划求解器求解 \(\alpha\) 即可,然后再根据 KKT 条件求出 \(w,\rho\),那么问题来了,数据跨越了零点怎么办? 做法很简单,使用映射函数将数据映射到一个空间,在该空间上数据不横跨原点,比如使用高斯核(\(\Phi(x)=\exp \left(-x^{2}\right) \cdot\left(1, \sqrt{\frac{2}{1 !}} x, \sqrt{\frac{2^{2}}{2 !}} x^{2}, \ldots\right)\))或二阶多项式核(\(\Phi_{2}(\mathbf{x})=\left(1, x_{1}, x_{2}, \ldots, x_{d}, x_{1}^{2}, x_{1} x_{2}, \ldots, x_{1} x_{d}, x_{2} x_{1}, x_{2}^{2}, \ldots, x_{2} x_{d}, \ldots, x_{d}^{2}\right)\)),可以看出其中有很多的恒非负数项,也就是在一个轴的一边,不会横跨原点。但是这都是博主的猜测,如果有读者看到论文的讲解部分可以留言纠正(英语水平有限🤷♂️)。
SVDD
另一种方法则是 SVDD,是在其同名论文《Support Vector Data Description》中由 DAVID M.J. TAX 等人提出。相比于 OCSVM,SVDD 定义了一个模型,该模型给出了一个包围全部数据的封闭边界:超球体。球体的特征是中心 \(a\) 和半径 \(R>0\)。我们通过最小化 \(R^2\) 来最小化球体的体积,并要求球体包含所有训练样本 \(x_i\)。这与Schólkopf、Burges和Vapnik(1995)中用于估计分类器的VC维数的方法(由包围数据的最小球体的直径限定)相同。并且文章中证明了该方法与 OCSVM 求解的超平面相似。其最优化目标如下:
\[\begin{aligned} \mathop{\min} \limits_ { R , a } & R ^ { 2 } + C \sum _ { i } \xi _ { i } \\
s . t . & \left\| \mathbf { x } _ { i } - \mathbf { a } \right\| ^ { 2 } \leq R ^ { 2 } + \xi _ { i } , \quad \xi _ { i } \geq 0 \quad \forall i \end{aligned}
\]
其中 \(C\) 用于控制误差的容忍度。同时为了求解对偶问题使用核技巧,这里使用 Lagrange 乘数 \(\alpha_i > 0,\gamma_i > 0\),可以写出拉格朗日方程:
\[\begin{aligned} L \left( R , \mathbf { a } , \alpha _ { i } , \gamma _ { i } , \xi _ { i } \right) = & R ^ { 2 } + C \sum _ { i } \xi _ { i } \\ & - \sum_i \alpha _ { i } \left\{ R ^ { 2 } + \xi _ { i } - \left( \left\| \mathbf { x } _ { i } \right\| ^ { 2 } - 2 \mathbf { a } \cdot \mathbf { x } _ { i } + \| \mathbf { a } \| ^ { 2 } \right) \right\} - \sum \gamma _ { i } \xi _ { i } \end{aligned}
\]
求偏导为零,可以得出:
\[\begin{aligned} \frac { \partial L } { \partial R } = 0 : & \qquad \sum _ { i } \alpha _ { i } = 1 \\ \frac { \partial L } { \partial \mathbf { a } } = 0 : & \qquad \mathbf { a } = \frac { \sum _ { i } \alpha _ { i } \mathbf { x } _ { i } } { \sum _ { i } \alpha _ { i } } = \sum _ { i } \alpha _ { i } \mathbf { x } _ { i } \\ \frac { \partial L } { \partial \xi _ { i } } = 0 : & \qquad C - \alpha _ { i } - \gamma _ { i } = 0 \end{aligned}
\]
通过上述第三个式子可以得出:
\[0 \leq \alpha _ { i } \leq C
\]
拉格朗日方程可以重写为:
\[L = \sum _ { i } \alpha _ { i } \left( \mathbf { x } _ { i } \cdot \mathbf { x } _ { i } \right) - \sum _ { i , j } \alpha _ { i } \alpha _ { j } \left( \mathbf { x } _ { i } \cdot \mathbf { x } _ { j } \right)
\]
那么该优化目标可以重写为:
\[\max _ { \boldsymbol { \alpha } } \sum _ { i } \alpha _ { i } \left( \mathbf { x } _ { i } \cdot \mathbf { x } _ { i } \right) - \sum _ { i , j } \alpha _ { i } \alpha _ { j } \left( \mathbf { x } _ { i } \cdot \mathbf { x } _ { j } \right) \text { subject to } 0 \leq \alpha _ { i } \leq C
\]
之后使用二次规划求解器求解 \(\alpha\) 即可,然后再根据 KKT 条件求出 \(R,a,\xi\) 即可。
参考论文有:《Support Vector Data Description》,《Support Vector Method for Novelty Detection》,《Estimating the Support of a High-Dimensional Distribution》



 浙公网安备 33010602011771号
浙公网安备 33010602011771号