LibTorch | 使用神经网络求解一维稳态对流扩散方程

0. 写在前面

本文将使用基于LibTorch（PyTorch C++接口）的神经网络求解器，对一维稳态对流扩散方程进行求解，文中仅对神经网络求解器对特定问题的求解能力进行了介绍，单纯一个无监督学习问题，未涉及迁移到其他问题的适用性问题等。水平有限，如有问题还希望读者斧正。研究问题参考自教科书\(^{[1]}\)示例 8.3。

目录

• 0. 写在前面
• 1. 问题描述
• 3. 解析解
• 4. 神经网络
  • 4.1 网络结构
  • 4.2 源项代码
  • 4.3 训练代码
  • 4.4 CMakeLists.txt
• 5. 结果处理
• 6. 后记
• 参考文献

1. 问题描述

一维稳态对流扩散方程为

\[\nabla \cdot \left( \vec{u}\phi \right) = \nabla\cdot \left( \Gamma \nabla\phi \right) + S \]

其中，均匀恒定速度 \(u=2.0 \mathrm{m/s}\) ，运动粘性系数 \(\Gamma = 0.03 \mathrm{m^2/s}\) ，源项 \(S\) 的形式后文将叙述。

假设一维计算域长度为 \(L=1.5 \mathrm{m}\)，其上分布有均匀恒定速度场；待求物理量为 \(\phi\)，边界条件为左侧（\(x=0\)）处给定一类边界条件（\(\phi=0\)），右侧（\(x=L\)）处给定二类边界条件（\(\phi_{,x}=0\)）。如下图（图片来自教科书\(^{[1]}\)，图8.7）所示。

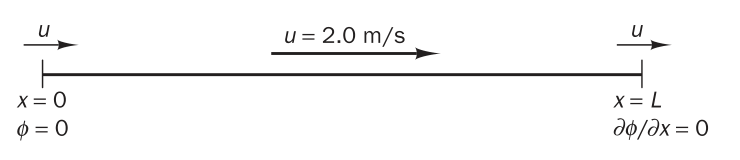
在计算域上源项分布如下图（图片来自教科书\(^{[1]}\)，图8.8）所示：

其中，\(a=-200\)，\(b=100\)，\(x_1=0.6\)，\(x_2=0.2\)。

源项数学表达式如式（1）所示。

\[S = \left\{ \begin{aligned} -200 x + 100&, \ \ 0.0\leqslant x < 0.6 \\ 100 x -80 &, \ \ 0.6 \leqslant x < 0.8 \\ 0&, \ \ x \geqslant 0.8 \end{aligned} \right . \tag1 \]

3. 解析解

上述一维稳态对流扩散方程存在解析解（参考文献中公式直接计算数值不对，这里做了一些修改，如果错了还请读者斧正）：

\[\frac{\phi(x)}{0.75b/L^2}= -C_1 - C_2 \exp(Px) + \frac{a_0}{P^2}\left( Px +1\right) + \sum_{n=1}^{\infty} a_n\left(\frac{L}{n\pi}\right) \frac{ P \sin\left(\frac{n\pi x}{L}\right) + \left(\frac{n\pi}{L}\right)\cos\left(\frac{n\pi x}{L}\right) } { P^2 + \left(\frac{n\pi}{L}\right)^2 } \]

其中，

\[\begin{aligned} P&=\frac{u}{\Gamma} \\ C_2&=\frac{a_0}{P^2\exp\left(PL\right)} + \sum_{n=1}^{\infty} \frac{a_n\cos\left(n\pi\right)} {\exp\left(PL\right)\left[P^2 + \left(\frac{n\pi}{L}\right)^2\right]}\\ C_1&= -C_2 + \frac{a_0}{P^2} +\sum_{n=1}^{\infty} \frac{a_n}{P^2 + \left(\frac{n\pi}{L}\right)^2} \\ a_0&= \frac{\left(x_1+x_2\right)\left(ax_1+b\right)+bx_1}{2L}\\ a_n&= \frac{2L}{n^2\pi^2} \left\{ \left(\frac{a\left(x_1+x_2\right)+b}{x_2}\right)\cos\left(\frac{n\pi x_1}{L}\right) - \left[ a + \left(\frac{ax_1+b}{x_2}\right) \cos\left(\frac{n\pi\left(x_1+x_2\right)}{L}\right) \right] \right\}\\ \end{aligned} \]

使用下面代码绘制解析解曲线。

import math
import matplotlib.pyplot as plt

a = -200.0 # [1/m]
b =  100.0 # [1]

L = 1.5    # [m]

x_1 = 0.6  # [m]
x_2 = 0.2  # [m]

u     = 2.0  # [m/s]
Gamma = 0.03 # [m^2/s]

P     = u / Gamma # [1/m]
P2    = P * P     # [1/m^2]
expPL = math.exp( P * L )

num_terms = 20000

def a_n(n):
    if n == 0 :
        return ( ( x_1 + x_2 ) * ( a * x_1 + b ) + b * x_1 ) / ( 2.0 * L )
    else:
        alpha = n * math.pi / L
        term0 = 2.0 * L / n / n / math.pi / math.pi
        term1 = ( a * ( x_1 + x_2 ) + b ) / x_2 * math.cos( alpha * x_1  )
        term2 = a + ( a * x_1 + b ) / x_2 * math.cos( alpha * ( x_1 + x_2 ) )
        return term0 * ( term1 - term2 )

def C2():
    term0 = a_n(0) / P2 / expPL
    term1 = 0.0
    for i in range(1,num_terms + 1):
        alpha = i * math.pi / L
        coeff = ( P2 + alpha * alpha )
        term1 += a_n(i) / expPL * math.cos( i * math.pi ) / coeff

    return term0 + term1

def C1():
    term0 = C2()
    term1 = a_n(0) / P2
    term2 = 0.0
    for i in range(1,num_terms + 1):
        alpha = i * math.pi / L
        coeff = ( P2 + alpha * alpha )
        term2 += a_n(i) / coeff

    return -term0 + term1 + term2

def phi(x):
    term0 = C1()
    term1 = C2() * math.exp( P * x )
    term2 = a_n(0) / P2 * ( P * x + 1.0 )
    term3 = 0.0
    for i in range(1,num_terms + 1):
        alpha = i * math.pi / L
        coeff = ( P2 + alpha * alpha )
        term3 += a_n(i) / alpha * ( P * math.sin( alpha * x ) + alpha * math.cos( alpha * x ) ) / coeff

    return term0 + term1 - term2 - term3

x = []
y = []
num_points = 50
for i in range(num_points):
    x_ = L / ( num_points - 1 ) * i
    x.append( x_ )
    y.append( -phi(x_) * 0.75 * b / L / L ) # 这里对参考文献中的公式做了修改

plt.grid()
plt.xlim( 0, 1.5 )
plt.ylim( 0, 12  )
plt.plot( x, y )
plt.show()

图像如下所示：

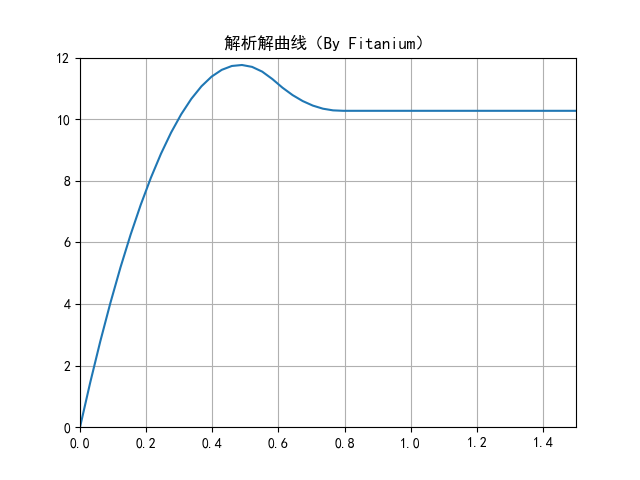
4. 神经网络

上述流畅处于稳态时，物理量 \(\phi\) 是位置 \(x\) 的函数，即 \(\phi=f(x)\)。那么我们这里的想法就是利用神经网络来表示这个函数，并通过利用机器学习方法（监督学习、自动微分）使该函数满足控制方程和边界条件。

对于上述关系，我们可以涉及类似下图中这种全连接神经网络（使用NN-SVG绘制）。

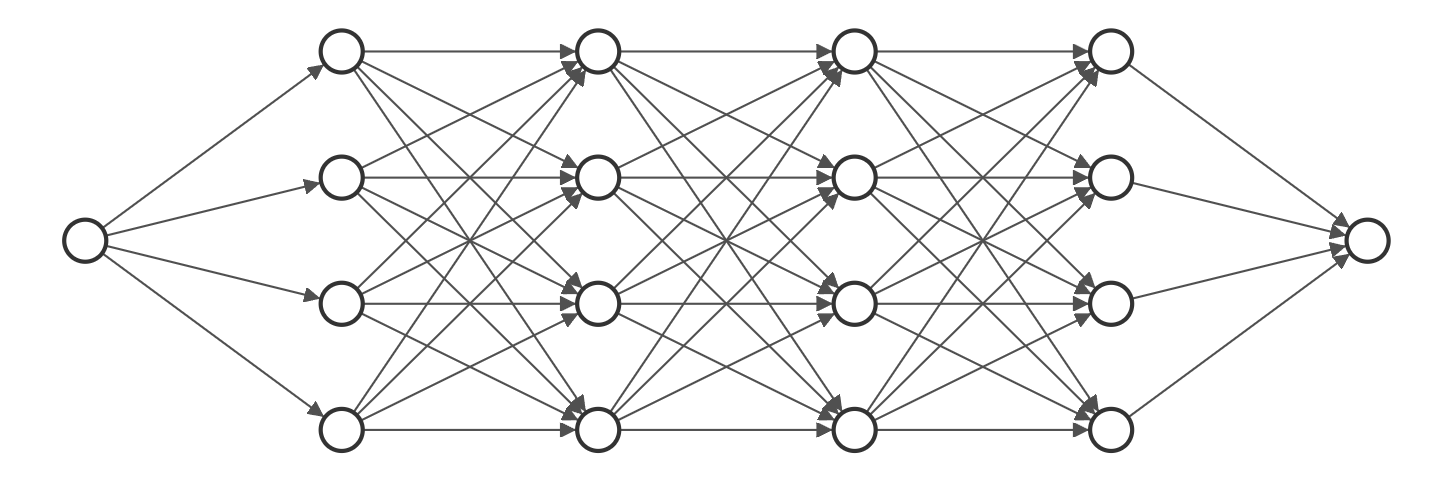
4.1 网络结构

这里我们设置了一个含有6层神经元的全连接神经网络，形式如上图所示，输入层和输出层均只有一个神经元，剩余4个隐藏层每层含有256个神经元。

神经网络类的声明如下，保存在文件 nets.hpp 文件中，其中需要声明向前传播算法方法以及相关模块变量。

#ifndef NETS_HPP
#define NETS_HPP

#include <torch\torch.h>
// 神经网络类
class Net : public torch::nn::Module {
public:
  Net(const int inDim, const int outDim);

  torch::Tensor forward(at::Tensor x);

private:
  torch::nn::Linear input{nullptr};
  torch::nn::Linear hidden0{nullptr};
  torch::nn::Linear hidden1{nullptr};
  torch::nn::Linear hidden2{nullptr};
  torch::nn::Linear output{nullptr};
};

#endif // NETS_HPP

接下来看一下神经网络的实现，我们将其实现保存在 nets.cpp 文件中，其中构造函数中将初始化这些模块变量；forward 方法为向前传播的实现，数据传播过程为 \(1\to 256\to 256\to 256\to 256\to 1\)，网络接受一个标量输入并最终返回一个标量输出；另外隐藏层全部采用 tanh 函数作为激活函数。

#include "nets.hpp"

Net::Net(const int inDim, const int outDim) {
  input = register_module("input", torch::nn::Linear(inDim, 256));
  hidden0 = register_module("hidden0", torch::nn::Linear(256, 256));
  hidden1 = register_module("hidden1", torch::nn::Linear(256, 256));
  hidden2 = register_module("hidden2", torch::nn::Linear(256, 256));
  output = register_module("output", torch::nn::Linear(256, outDim));
}

torch::Tensor Net::forward(at::Tensor x) {
  // 输入层   : 1   --> 隐藏层 0 : 256
  torch::Tensor phi = input->forward(x);
  phi = torch::tanh(phi); // 激活函数
  // 隐藏层 0 : 256 --> 隐藏层 1 : 256
  phi = hidden0->forward(phi);
  phi = torch::tanh(phi); // 激活函数
  // 隐藏层 1 : 256 --> 隐藏层 2 : 256
  phi = hidden1->forward(phi);
  phi = torch::tanh(phi); // 激活函数
  // 隐藏层 2 : 256 --> 隐藏层 3 : 256
  phi = hidden2->forward(phi);
  phi = torch::tanh(phi); // 激活函数
  // 隐藏层 3 : 256 --> 输出层   : 1
  phi = output->forward(phi);
  //
  return phi;
}

4.2 源项代码

分布源项为分段函数，这块比较简单，直接给出头文件和实现。

函数声明保存在 utils.hpp 文件中。

#ifndef UTILS_HPP
#define UTILS_HPP

float Source(const float x);

#endif // UTILS_HPP

函数实现保存在 utils.cpp 文件中。

#include "utils.hpp"

float Source(const float x) {
  if (x < 0.6) {
    return -200.0 * x + 100.0;
  } else if (x > 0.8) {
    return 0.0;
  } else {
    return 100.0 * x - 80.0;
  }
}

4.3 训练代码

这里，我们将训练代码保存在 main.cpp 文件中。由于空间位置不变，我们在迭代训练外构造输入参数。

graph TB A(开始) --> B[构造输入] B[构造输入] --> C[初始化神经网络和优化器] C[初始化神经网络和优化器] --> D[迭代训练] D[迭代训练] --> E[向前传播] E[向前传播] --> F[构造损失函数] F[构造损失函数] --> G[反向传播] G[反向传播] --> H[更新参数] H[更新参数] --> I[判断收敛] I[判断收敛] --> J{是否收敛} J{是否收敛} -- 是 --> K(结束) J{是否收敛} -- 否 --> D[迭代训练]

代码实现如下所示，其中计算PDE的损失时用到了自动微分，可参考笔者之前的随笔LibTorch 自动微分。

#include <fstream>
#include <iomanip>
#include <iostream>
#include <string>

#include "nets.hpp"
#include "utils.hpp"

int main(int argc, char *atgv[]) {
  std::cout << std::scientific << std::setprecision(7);

  const double L = 1.5;      // 计算域长度
  const int numElement = 20; // 输入点个数

  // 构造输入，维度为[N,1]，N行，每行为一个输入，维度为1
  std::vector<float> x;
  for (int i = 0; i < numElement; ++i) {
    x.push_back(L / double(numElement - 1) * double(i));
  }
  torch::Tensor xT = torch::from_blob(x.data(), {numElement, 1}, torch::kFloat)
                         .requires_grad_(true);

  // 初始化神经网络和随机梯度下降优化器
  std::shared_ptr<Net> net = std::make_shared<Net>(1, 1);
  std::shared_ptr<torch::optim::SGD> optimizer =
      std::make_shared<torch::optim::SGD>(net->parameters(), 1.e-4);

  // 开始迭代训练
  double lossVal = 10;
  int epochIdx = 0;
  std::vector<float> sol(numElement);
  while (lossVal > 1.e-3) {
    // 向前传播，最终输出是一个[N,1]的输出
    torch::Tensor out = net->forward(xT);

    // 构造损失函数（由3部分组成，PDE和两侧边界条件）
    auto ones = torch::ones_like(out);
    torch::Tensor ddx =
        torch::autograd::grad({out}, {xT}, {ones}, true, true, false)[0];
    torch::Tensor d2dx2 =
        torch::autograd::grad({ddx}, {xT}, {ones}, true, true, false)[0];
    auto sourceTerm = torch::zeros_like(out);
    for (int i = 0; i < numElement; ++i) {
      sourceTerm[i][0] = Source(xT[i][0].item<float>());
    }
    auto pde = 2.0 * ddx - 0.03 * d2dx2;
    auto pdeLoss = torch::mse_loss(pde, sourceTerm); // 偏微分方程

    auto tag1 = torch::zeros_like(out);
    for (int i = 0; i < numElement; ++i) {
      if (i == 0) {
        tag1[i][0] = 0.0;
      } else {
        tag1[i][0] = out[i][0].item<float>();
      }
    }
    auto bndLoss1 = torch::mse_loss(out, tag1); // 左侧边界条件

    auto tag2 = torch::zeros_like(ddx);
    for (int i = 0; i < numElement; ++i) {
      if (i == numElement - 1) {
        tag2[i][0] = 0.0;
      } else {
        tag2[i][0] = ddx[i][0].item<float>();
      }
    }
    auto bndLoss2 = torch::mse_loss(ddx, tag2); // 右侧边界条件

    auto totalLoss = pdeLoss + bndLoss1 + bndLoss2;

    // 反向传播
    optimizer->zero_grad();
    totalLoss.backward();
    optimizer->step();

    // 打印日志
    lossVal = totalLoss.item<float>();
    std::cout << "PDE_LOSS: " << pdeLoss.item<float>()
              << ", BND_LOSS1: " << bndLoss1.item<float>()
              << ", BND_LOSS2: " << bndLoss2.item<float>()
              << ", TOTAL_LOSS: " << lossVal << ", EPOCH.IDX: " << epochIdx
              << std::endl;

    epochIdx += 1;

    for (int i = 0; i < numElement; ++i) {
      sol[i] = out[i][0].item<float>();
    }
  }

  // 保存结果
  std::ofstream os;
  os.open("solution.txt", std::ios::out);
  for (int i = 0; i < numElement; ++i) {
    os << x[i] << " " << sol[i] << std::endl;
  }
  os.close();

  return 0;
}

4.4 CMakeLists.txt

这里使用 CMake 管理程序代码，内容如下所示。

cmake_minimum_required( VERSION 3.8 )

project( LibTorch)

set( CMAKE_CXX_STANDARD 14 )

set( INSTALL_PREFIX "D:/SoftwarePackage" )

## LibTorch
find_package(Torch REQUIRED PATHS "${INSTALL_PREFIX}/libtorch/share/cmake/Torch")
link_directories( "${INSTALL_PREFIX}/libtorch/lib" )

# My own code 
include_directories( . )
set(SRCS
    nets.cpp
    utils.cpp
)

set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} ${TORCH_CXX_FLAGS}" )
add_executable ( ${PROJECT_NAME} main.cpp ${SRCS} )
target_link_libraries(${PROJECT_NAME} ${TORCH_LIBRARIES} )

5. 结果处理

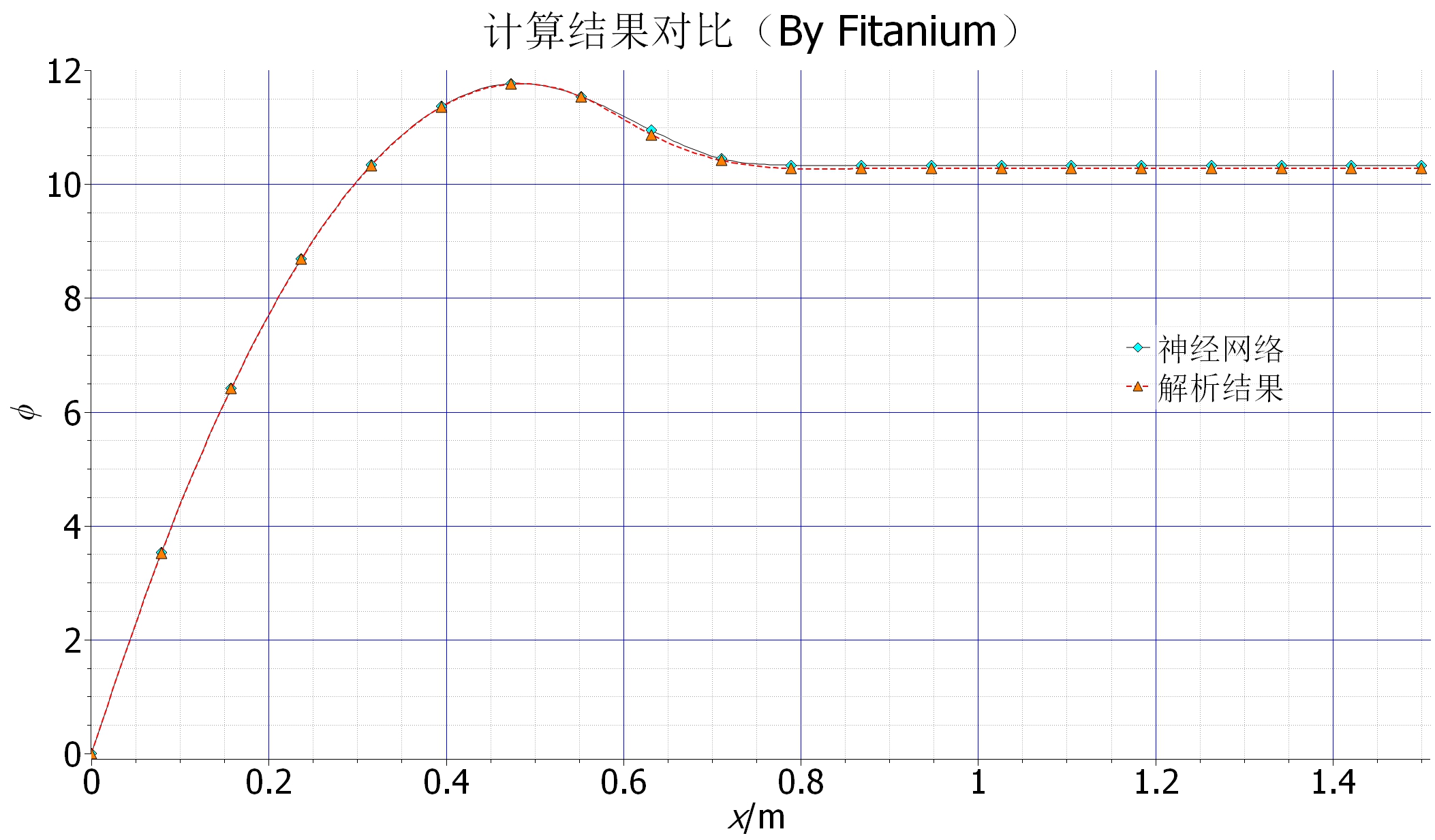
神经网络训练了近4万6千多次才满足收敛标准，其实还是挺慢的。其中误差最主要来自于神经网络无法满足偏微分方程（PDE），这和很多因素有关，比如网络结构，收敛判据等。

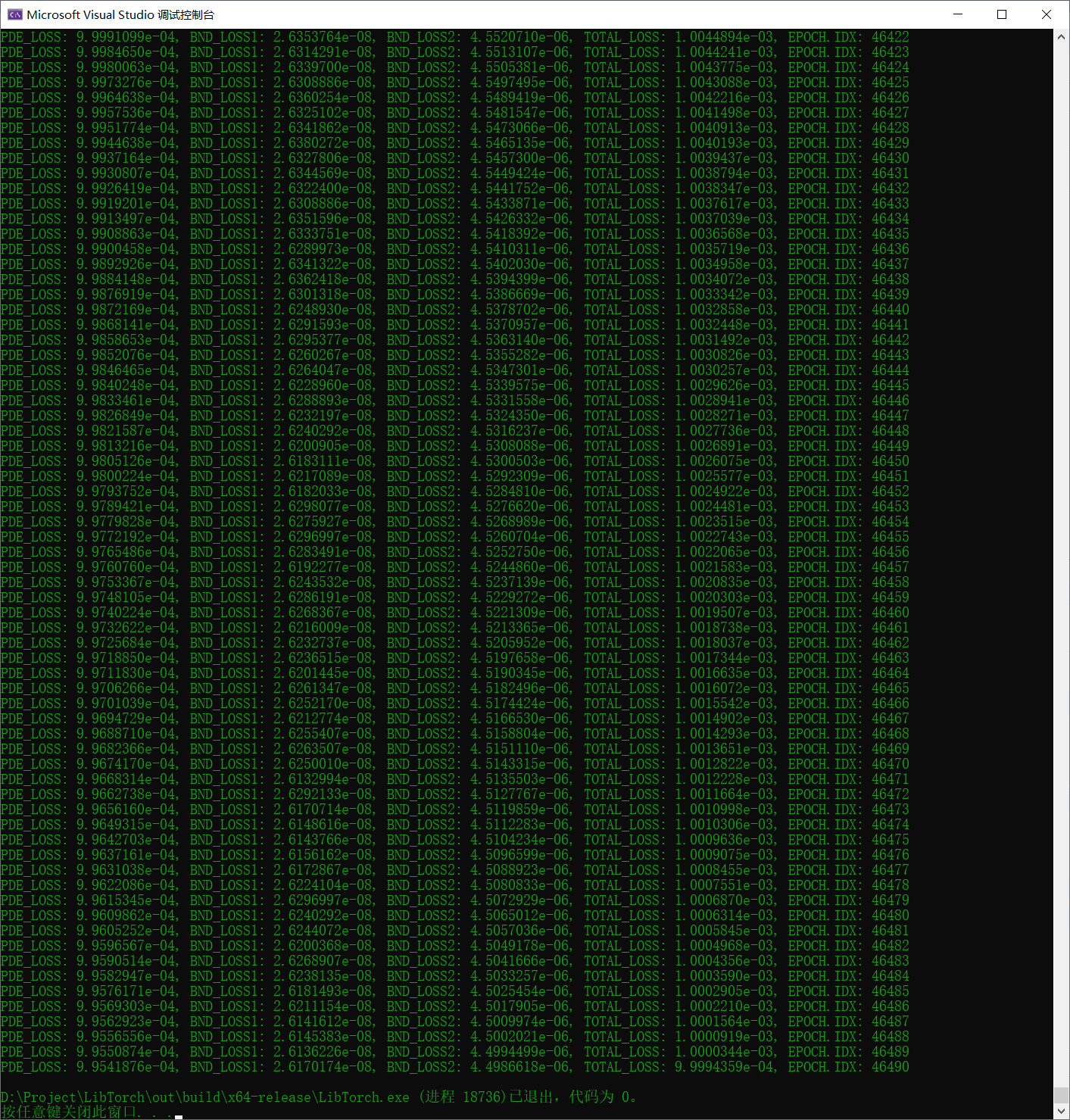
从下图数值结果来看，训练的神经网络给出的结果与解析解能够较好吻合，后段有一个明显的误差，但是相对较小，这个误差应该来自网络本身，网络结构简单，改进空间应该还是比较大。

本文写的比较简单，也没有使用批训练。此外，感兴趣的小伙伴可以尝试使用OpenFOAM求解，可参考笔者之前的随笔 OpenFOAM 编程 | One-Dimensional Transient Heat Conduction 。

6. 后记

发了这个随笔之后，有几个小伙伴提出了一些评论和问题（非常感谢能够提出一些东西让我思考），感觉挺不错的，我也想把自己的理解在此处记录一下，欢迎大家交流讨论：

1. 训练的这个神经网络可以用来求解其他类似问题吗？
   坦言之，这个随笔里的神经网络只能求解这个问题，其他问题解不了。第一点就是清楚一个模型的作用，笔者随笔里提到的模型只是假设了一个稳态解，然后用神经网络去学习这个解，因此它的作用是给定 \(x\) 坐标，输出对应的结果 \(\phi\)；第二点就是，这里的神经网络不是一个通用的求解器，对于这个问题训练完成后，模型参数确定了，对于其他问题，训练同样一个神经网络，参数可能完全不一样，所以很难说适用其他问题（大概率是不能）；第三点就是，如何定义“其它问题”，PDE形式、边界条件、初始条件，已知条件等的不同都会导致问题改变，即使使用有限体积法，所形成的的系数矩阵和右端项也是不一样的，而直接迁移使用对于神经网络来说有点太难了，所以结论仍然是解不了。

2. 为什么没有测试集？预测能力体现在哪里？
   在第一个问题中提到了，我们假定了稳态解的形式 \(\phi=f(x)\)，所以坐标 \(x\) 需要作为训练数据使用；而我们并没有 \((x_i,\phi_i)\) 这样的已知数据对（笔者也没有使用解析解，不想把这个神经网络变成一个单纯的监督学习任务，虽然加入部分已知数据可以加快收敛）；但是笔者的随笔里确实缺少测试过程，应该添加一些非训练点用作预测使用，笔者之后会补上。

代码修改如下

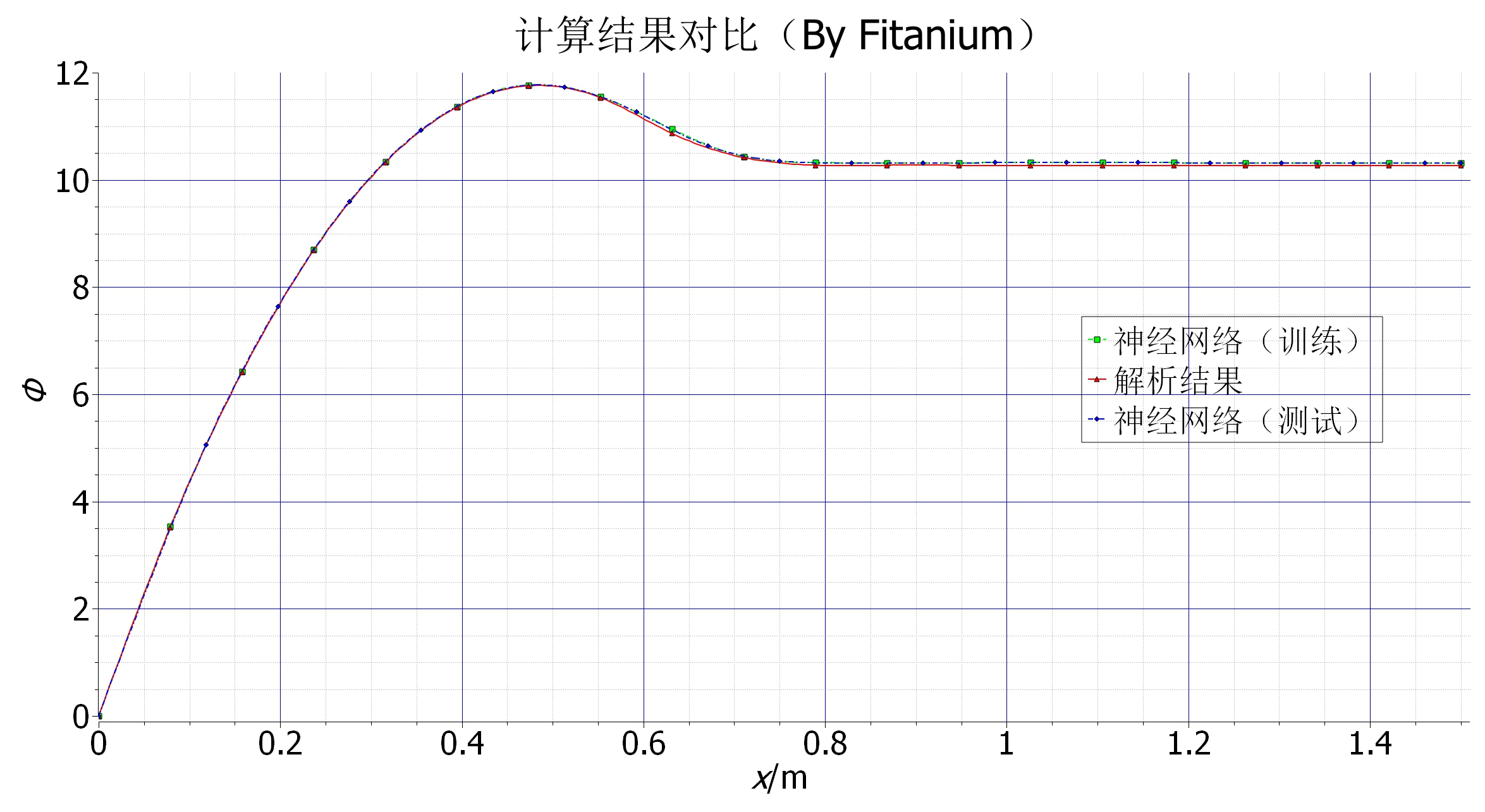
// 测试坐标点
std::vector<float> x_test;
for (int i = 0; i < numElement; ++i) {
  if (i == 0 || i == numElement - 1) {
    x_test.push_back(x[i]);
  } else {
    x_test.push_back(x[i] + L / double(numElement - 1) * 0.5); // 这里训练数据做了偏移
  }
}
torch::Tensor x_testT =
    torch::from_blob(x_test.data(), {numElement, 1}, torch::kFloat);

// 训练结束后，获得测试结果
torch::Tensor out = net->forward(x_testT);
os.open("solution_test.txt", std::ios::out);
for (int i = 0; i < numElement; ++i) {
  os << x_test[i] << " " << out[i][0].item<float>() << std::endl;
}
os.close();

然后，把训练结果、解析结果和测试结果绘制在同一张图里。

3. 这个随笔的意义在哪里？
   在于使用神经网络去得到一个变为分方程的解，侧重介绍这个无监督学习方法（自动微分、反向传播）的用法。

4. 训练数据点怎么选取的？
   均匀选取的，本文通过误差反向传播和自动微分求出解的形式，本文算例对坐标点没有什么要求，可能其它情况会有别的要求。

5. 不会过拟合吗？
   应该不会，这个问题和监督学习有挺大的区别，在于损失函数的形式，除左侧边界条件外，损失函数的其他部分（PDE和右侧边界）没有直接用到模型的输出，因此个人感觉不会过拟合。

参考文献

[1] H. Versteeg , W. Malalasekera. Introduction to Computational Fluid Dynamics, An: The Finite Volume Method 2nd Edition[M]. Pearson. 2007.