LibTorch 多项分布

最近在学习过程中需要对服从某种分布的离散型随机变量进行抽样，在LibTroch中查到了torch::multinomial（多项分布），该方法的接口如下：

at::Tensor multinomial(
    const at::Tensor & self,   // 概率分布
    int64_t num_samples,       // 一次抽样个数
    bool replacement=false,    // 是否重复抽样，默认不重复抽样（无放回地）
    c10::optional<at::Generator> generator=c10::nullopt // 随机数生成器
)

使用时需要注意几点：

• 第一个参数：给定的概率分布加和不为1时，将自动归一化。例如给定某个二项分布{0：0.2，1：0.3}，那么抽样时取0的概率为$0.2/(0.2+0.3) = 0.4$，取1的概率为$0.3/(0.2+0.3) = 0.6$。
• 第三个参数：设置为真时，将重复抽样（有放回地）。如果一次抽样个数等于样本空间个数，这里需要设置为真。

---

下面是一个多项分布的例子，假设样本空间为4，其概率分布如下

$x_i$	0	1	2	3
$p(x_i)$	0.1	0.2	0.3	0.4

统计10000000次抽样结果的频率，代码如下所示

#include <iostream>
#include <torch/torch.h>
 
int main(int argc, char* argv[])
{
    // 概率分布（加和不为一时，将自动进行归一化处理）
    torch::Tensor probs = torch::tensor({0.1, 0.2, 0.3, 0.4});
 
    int num_0 = 0;
    int num_1 = 0;
    int num_2 = 0;
    int num_3 = 0;
    for (int i = 1; i <= 10000000; ++i)
    {
        int sample = torch::multinomial(probs, 1, true).item<long>(); // 抽样
        switch (sample)
        {
            case 0:
                num_0 += 1;
                break;
            case 1:
                num_1 += 1;
                break;
            case 2:
                num_2 += 1;
                break;
            case 3:
                num_3 += 1;
                break;
            default:
                break;
        }
        std::cout << "freq of 0 is " << double(num_0) / i << std::endl
                  << "freq of 1 is " << double(num_1) / i << std::endl
                  << "freq of 2 is " << double(num_2) / i << std::endl
                  << "freq of 3 is " << double(num_3) / i << std::endl
                  << std::endl;
    }
 
    return 0;
}

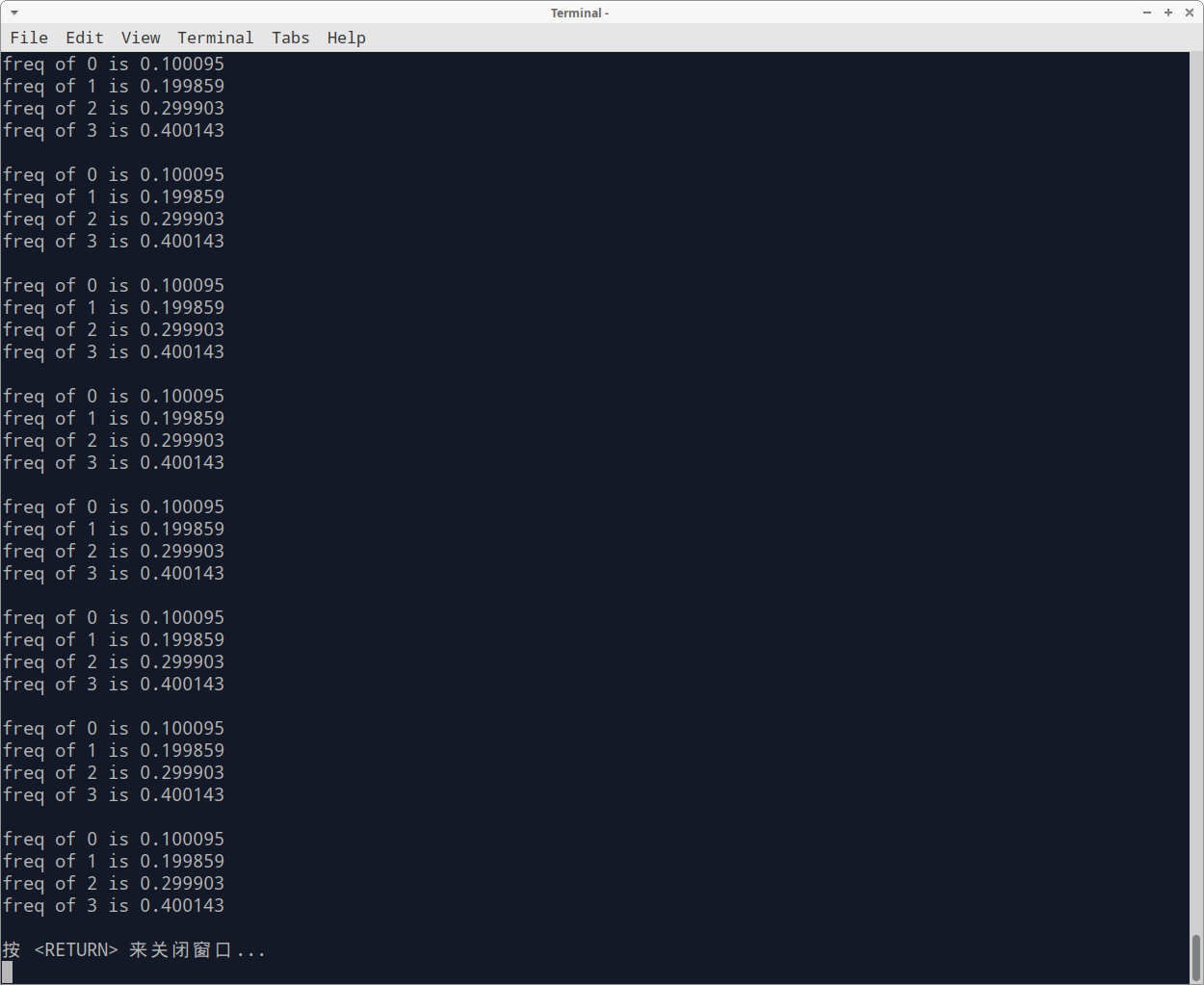
运行结果如下，每个事件的统计频率与其概率分布能够较好吻合。各位读者可以试一试将概率分布修改使其和值不为1，看看结果会是怎么样。。。

---

参考资料：
TORCH.MULTINOMIAL