7-2 最小重量机器设计问题 (25 分)
设某一机器由n个部件组成,每一种部件都可以从m个不同的供应商处购得。设wij是从供应商j 处购得的部件i的重量,cij是相应的价格。 试设计一个算法,给出总价格不超过d的最小重量机器设计。
输入格式:
第一行有3 个正整数n ,m和d, 0<n<30, 0<m<30, 接下来的2n 行,每行n个数。前n行是c,后n行是w。
输出格式:
输出计算出的最小重量,以及每个部件的供应商
输入样例:
3 3 4
1 2 3
3 2 1
2 2 2
1 2 3
3 2 1
2 2 2
结尾无空行
输出样例:
在这里给出相应的输出。例如:
4
1 3 1
代码:
#include <iostream>
#include <algorithm>
using namespace std;
int weight = 0;
int minweight = 10000;//得出的最小重量
int cost = 0;
int n, m, d;
int path[1000];
int result[1000];
int w[100][100];
int c[100][100];
void backtrack(int t)
{
if(t > n)
{
if(weight < minweight && cost <= d)//遇上更小的重量,记录最小重量以及其选择方式
{
minweight = weight;
for(int i = 1; i <= n; i++)
{
result[i] = path[i];
}
}
return;
}
else
{
for(int i = 1; i <= m; i++)
{
weight += w[t][i];
cost += c[t][i];
path[t] = i;//记录选择了的供应商
if(weight < minweight && cost <= d)
backtrack(t + 1);
weight -= w[t][i];
cost -= c[t][i];
}
}
}
int main(int argc, char** argv) {
cin >> n >> m >> d;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
cin >> c[i][j];
}
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
cin >> w[i][j];
}
}
backtrack(1);
cout << minweight << endl;
for(int i = 1; i <= n; i++)
cout << result[i] << " ";
// for(int i = 1; i <= n; i++)
// cout << path[i];
return 0;
}
1. 请用回溯法的方法分析“最小重量机器设计问题”
1.1 说明“最小重量机器设计问题"的解空间
解空间即供选择的所有可能
(1,1,1)(1,1,2)(1,1,3)
(1,2,1)(1,2,2)(1,2,3)
(1,3,1)(1,3,2)(1,3,3)
(2,1,1)(2,1,2)(2,1,3)
(2,2,1)(2,2,2)(2,2,3)
(2,3,1)(2,3,2)(2,3,3)
(3,1,1)(3,1,2)(3,1,3)
(3,2,1)(3,2,2)(3,2,3)
(3,3,1)(3,3,2)(3,3,3)
1.2 说明 “最小重量机器设计问题"的解空间树
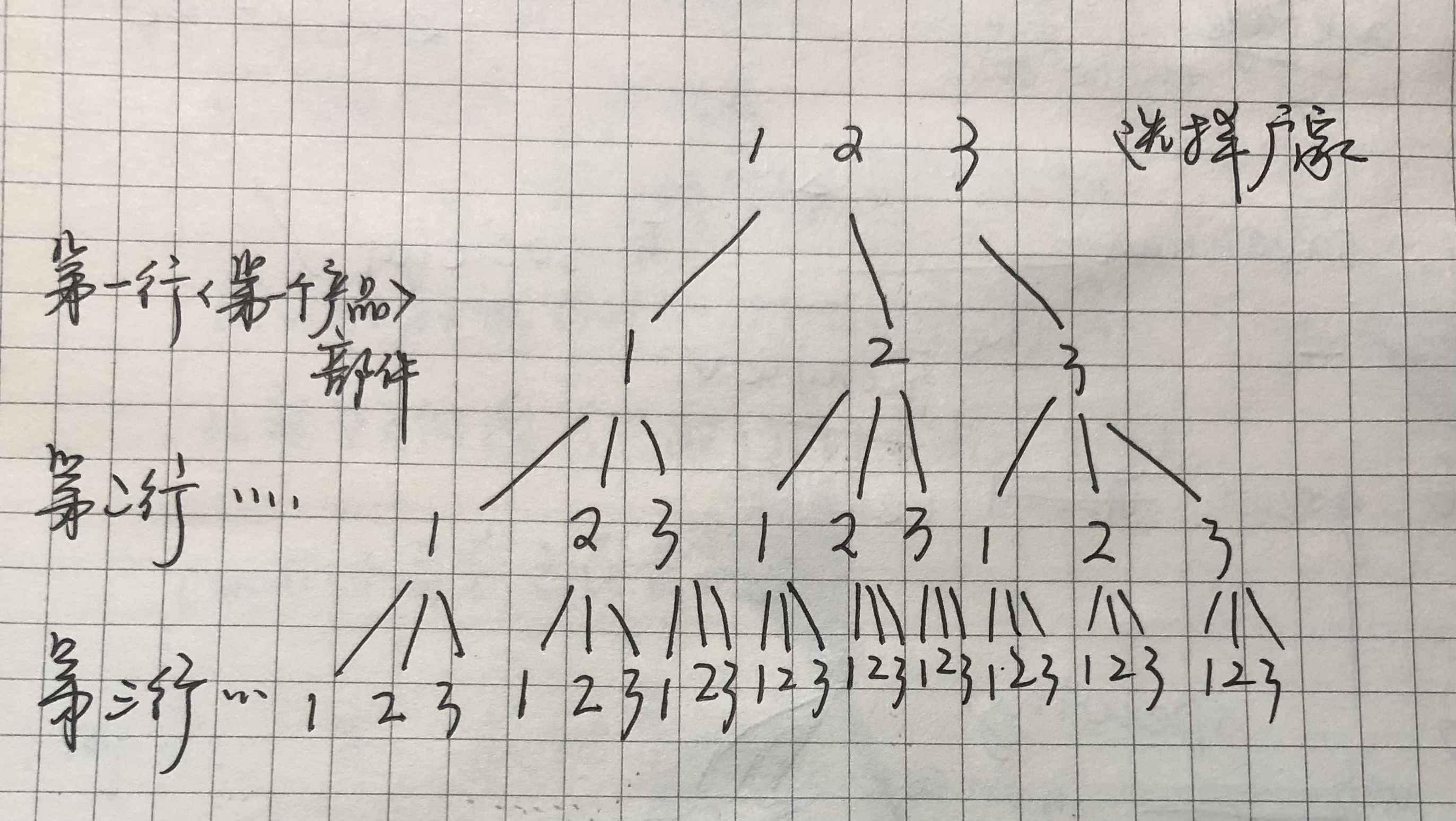
1.3 在遍历解空间树的过程中,每个结点的状态值是什么
(1)从第一个结点到当下结点的价值总和
(2)从第一个结点到当下结点的重量总和
2. 你对回溯算法的理解
有序地进行深度遍历,同时更新节点状态以查找出最优方案。要明确每个节点的状态值,遍历到叶子节点后,将更新过的状态值恢复,返回至上一节点(即回溯),继续进行遍历。

