【图像处理笔记】SIFT算法原理与源码分析
0 引言
特征提取就是从图像中提取显著并且具有可区分性和可匹配性的点结构。常见的点结构一般为图像内容中的角点、交叉点、闭合区域中心点等具有一定物理结构的点，而提取点结构的一般思想为构建能够区分其他图像结构的响应函数或者从特征线或轮廓中进行稀疏采样。Harris角点检测器便是运用二阶矩或自相关矩阵来加速局部极值搜索并保证方向的不变性。基于像素比较的特征提取方法也称为二值特征，通常具有极高的提取效率并具有一定的方向不变性以及所提取的特征点具有较高的重复率，对后续的匹配具有重要意义，然而这类方法受尺度和仿射变换的影响较大。针对上述问题，带有尺度信息的斑点特征成为特征提取的另一种形式，其最早是由Lindeberg 等人提出的高斯拉普拉斯（Laplace of Gaussian，LoG）函数响应来实现，并从中提出了尺度空间理论，其利用高斯响应函数的圆对称性和对局部团结构的极值响应特性以及对噪声抑制能力，通过不同高斯标准差实现在尺度空间上的极值搜索，从而提取对尺度、方向和噪声鲁棒的特征点并得到相应的尺度信息。为了避免大量的计算，D.Lowe 等人介绍了一种高斯差分（Difference-of-Gaussian，DoG）法来近似LoG的计算，并提出了著名的SIFT特征描述子。
SIFT是由Lowe[2004]开发的一个算法，用于提取图像中的不变特征。称它为变换的原因是，它会将图像数据变换为相对于局部图像特征的尺度不变坐标。SIFT是本章到目前为止讨论的最复杂的特征检测和描述方法。本节中用到了大量由实验确定的参数。因此，与前面介绍的许多方法不同，SIFT具有很强的探索性，因为我们目前所具备的知识还不能让我们将各种方法组合为一个能够求解单重方法所不能求解的问题的“系统”。因此，我们不得不通过实验确定控制更复杂系统性能的各种参数的相互作用。SIFT特征（称为关键点）对图像尺度和旋转是不变的，并且对仿射失真、三维视点变化、噪声和光照变化具有很强的鲁棒性。SIFT的输入是一幅图像，输出是一个n维特征向量，向量的元素是不变的特征描述子。
1 SIFT算法流程
Lowe将SIFT算法分为如下四步：
（1）尺度空间极值检测：搜索所有尺度上的图像位置。通过高斯差分函数来识别潜在的对于尺度和旋转不变的关键点。
（2）关键点定位：在每个候选的位置上，通过一个拟合精细的模型来确定位置和尺度。关键点的选择依据于它们的稳定程度。
（3）关键点方向确定：基于图像局部的梯度方向，分配给每个关键点位置一个或多个方向。所有后面的对图像数据的操作都相对于关键点的方向、尺度和位置进项变换，从而保证了对于这些变换的不变性。
（4）关键点描述：在每个关键点周围的邻域内，在选定的尺度上测量图像局部的梯度。这些梯度作为关键点的描述符，它允许比较大的局部形状的变形或光照变化。
1.1 尺度空间极值检测
1.1.1 尺度空间
SIFT算法的第一阶段是找到对尺度变化不变的图像位置。将图像利用不同的尺度参数进行平滑后得到一堆图像，目的是模拟图像的尺度减小出现的细节损失。在SIFT中，用于实现平滑的是高斯核，因此尺度参数是标准差。标准差的大小决定图像的平滑程度，大尺度对应图像的概貌特征，小尺度对应图像的细节特征。大的值对应粗糙尺度(低分辨率)，小的值对应精细尺度(高分辨率)。因此灰度图像f(x,y)的尺度空间 L(x,y,σ)是f与一个可变尺度高斯核G(x,y,σ)的卷积：
式中，尺度由参数σ控制，G的形式如下：
输入图像f(x,y)依次与标准差为σ，kσ，k2σ，k3σ，...，的高斯核卷积，生成一堆由一个常量因子k分隔的高斯滤波（平滑）图像。
Q1: 怎么理解平滑建立的尺度空间？
对于一副图像，近距离观察和远距离观察看到的图像效果是不同的，前者比较清晰，通过前者能看到图像的一些细节信息，后者比较模糊，通过后者能看到图像的一些轮廓的信息，这就是图像的尺度，图像的尺度是自然存在的，并不是人为创造的。尺度空间中各尺度图像的模糊程度逐渐变大，能够模拟人在距离目标由近到远时目标在视网膜上的形成过程。在平滑后图像上的一点，包含的是原图中一块像素的信息，属于语义层面的多尺度。
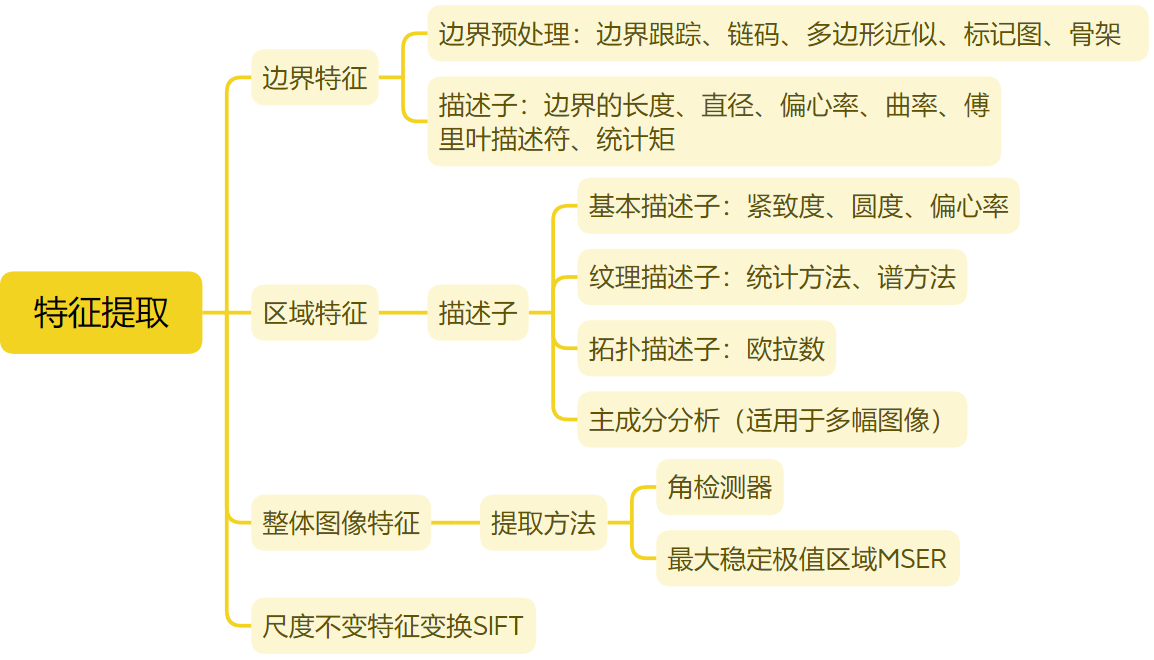
1.1.2 高斯金字塔
图像金字塔广泛应用于各种视觉应用中。图像金字塔是图像的集合，它是由原始图像产生，连续降采样，直到达到一些期望的停止点。常出现的两种金字塔是：高斯金字塔和拉普拉斯金字塔。高斯金字塔用于降采样，当我们要从金字塔中较低的图像重构上采样图像时，需要拉普拉斯金字塔。SIFT中的高斯金字塔与最原始的高斯金字塔有些区别，因为它在构造尺度空间时，将这些不同尺度图像分为了O个Octave、每个Octave又分为了S层。
- 对于O的选择：O = log2(min(M,N))-3，M、N指原图像的长和宽，求最小值后开log再减3
- 对于S的选择：S = n + 3，其中，n指我们希望提取多少个图片中的特征。当S=2时，每个Octave有5层。为什么要+3呢？因为后面要差分，5层差分得到4层，然后每层要和上下两层比较，也就是4层中有两层没法比较，只留下两层，即n是2。
- 关于比例因子k：为了满足尺度变化的连续性，某一组的每一层应该相差一个k倍。对于Octave2中的第一层，我们取Octave1中的倒数第三层，因为倒数第三层的σ为knσ，也就是为了凑2σ，达到一个隔点取点的降采样效果。所以有knσ=2σ，得k=1/n，当n=2时，k等于√2。即Octave1：【σ，...，knσ，kn+1σ，kn+2σ，kn+3σ】,Octave2：【knσ，kn+1σ，kn+2σ，kn+3σ,kn+4σ】
Q2:按照尺度空间的理论，模糊就已经改变尺度了，为什么还要下采样呢？
void SIFT_Impl::buildGaussianPyramid(const Mat& base, std::vector<Mat>& pyr, int nOctaves) const
{
CV_TRACE_FUNCTION();
std::vector<double> sig(nOctaveLayers + 3);
pyr.resize(nOctaves * (nOctaveLayers + 3));
// precompute Gaussian sigmas using the following formula:
// \sigma_{total}^2 = \sigma_{i}^2 + \sigma_{i-1}^2
sig[0] = sigma;
double k = std::pow(2., 1. / nOctaveLayers);
for (int i = 1; i < nOctaveLayers + 3; i++)
{
double sig_prev = std::pow(k, (double)(i - 1)) * sigma;
double sig_total = sig_prev * k;
//为了降低运算，将大尺度的高斯算子拆分为2个小尺度高斯算子的卷积
sig[i] = std::sqrt(sig_total * sig_total - sig_prev * sig_prev);
}
for (int o = 0; o < nOctaves; o++)
{
for (int i = 0; i < nOctaveLayers + 3; i++)
{
Mat& dst = pyr[o * (nOctaveLayers + 3) + i];
if (o == 0 && i == 0)
dst = base;
// base of new octave is halved image from end of previous octave
else if (i == 0)//每个Octave的第一层，都是上一个Octave的倒数第三层的下采样，这样可以得到连续的尺度
{
const Mat& src = pyr[(o - 1) * (nOctaveLayers + 3) + nOctaveLayers];
resize(src, dst, Size(src.cols / 2, src.rows / 2),
0, 0, INTER_NEAREST);
}
else
{ //每组中下一层由上一层高斯模糊得到，直接对第一层高斯模糊计算量太大
const Mat& src = pyr[o * (nOctaveLayers + 3) + i - 1];
GaussianBlur(src, dst, Size(), sig[i], sig[i]);
}
}
}
}
1.1.3 高斯拉普拉斯(LoG)金字塔
在介绍边缘检测的博客中，我们了解到二阶导数的过零点可以用于确定粗边缘的中心位置。Marr-Hildreth边缘检测子利用高斯拉普拉斯（LoG）函数来检测边缘，检测算子可以为不同尺度，大算子检测模糊边缘，小算子检测清晰的细节。LoG也是一种比较常用的斑点检测方法。
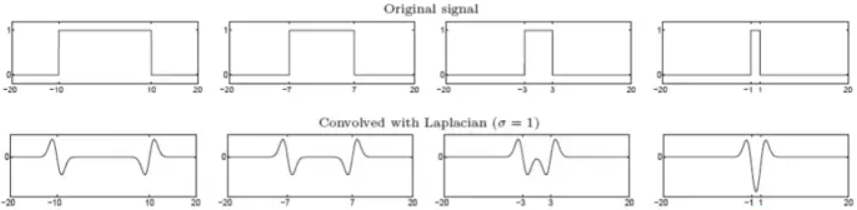
上面一行原始信号类似于一条线的灰度剖面，下面是在相同尺度σ下的LoG结果。可以看出总的LoG曲线其实是两条边界上LoG函数的结果的叠加，当两条边界足够接近时，可以将这个原始信号看作一个blob，两个LoG函数的结果也合二为一得到一个极值点，这个极值点对应blob的中心。所以边缘检测对应的是LoG的过零点，而斑点检测对应的是LoG的极值点。
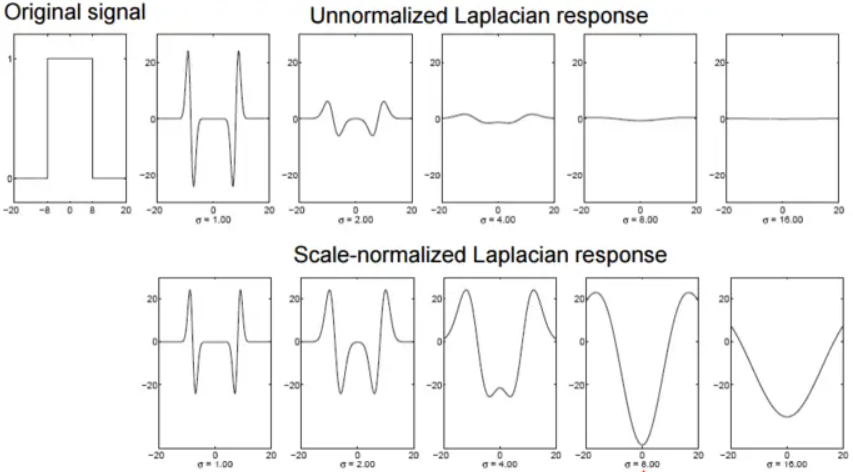
检测blob时，需要选择合适的尺度，然后LOG可以通过检测极值点来检测blob。上图第一行为原信号对不同尺度LoG的响应，可以发现随着尺度的不断增大，LoG曲线由双波谷逐渐融合成单波谷，但是响应的幅值越来越弱。这是因为，随着尺度的增大，LoG算子的最大幅度逐渐减小，导致响应也随着尺度的增大而减小。因此应该使用σ2对LoG进行归一化，即σ2▽2G。上图第二行是归一化后的拉普拉斯响应。归一化后选择产生最强响应的尺度，在该尺度上对应的极值就是blob的中心位置。理论表明，对于一个圆形blob，当二维LoG算子的零点值曲线和目标圆形边缘重合时取得最强响应。
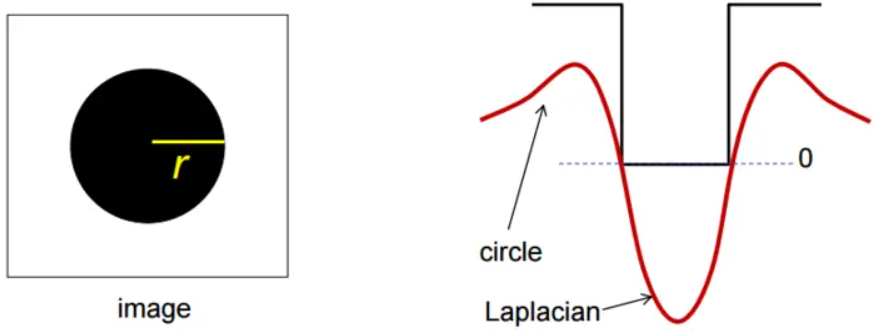
即令LoG=0，
得到σ = r/√2。使用LoG寻找斑点时不仅在图像上寻找极值点，还要求在尺度空间上也是极值点。也就是检测在尺度空间和图像空间都是极值的点，就是blob区域的中心点。
1.1.4 高斯差分(DOG)金字塔
二元连续高斯函数G(x,y,σ)对σ求导，可得
而LoG函数为
两者仅相差一个σ，即
根据极限又可以得到
因此，当k≈1时，有
两个不同方差的高斯函数相减记作DoG，和尺度归一化的LoG只相差一个倍数k-1，这个倍数是一个常数，不影响极值点检测。DoG计算速度快，LoG更精确。因此，我们用高斯差DoG近似高斯拉普拉斯LoG，具体做法就是将相邻两层的高斯尺度图像相减：
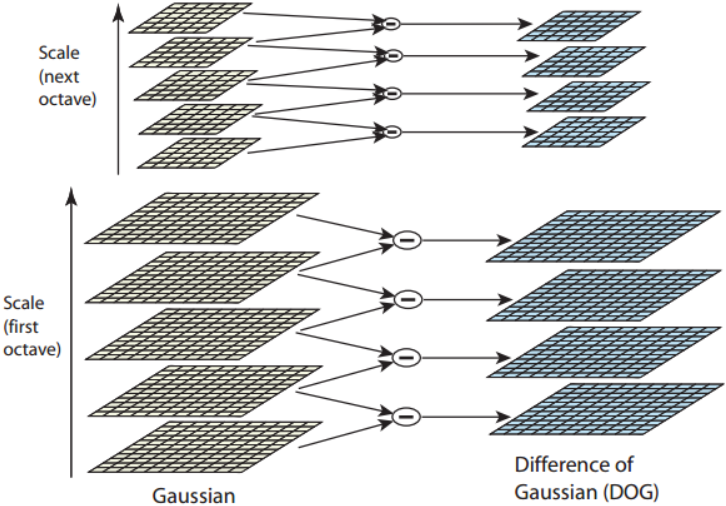为了在每组中检测n个尺度的极值点，DOG金字塔每组需n+2层图像，因为DOG金字塔的每一层和其上下两层比较得到极值点，第一层和最后一层是不能检测极值点的，而DOG金字塔由高斯金字塔相邻两层相减得到，则高斯金字塔每组需n+3层图像。
OpenCV构建DoG金字塔源码
并行计算，共nOctaves个Octave，每个Octave有nOctaveLayers+3层，共nOctaves * (nOctaveLayers + 2)个差分计算。
class buildDoGPyramidComputer : public ParallelLoopBody
{
public:
buildDoGPyramidComputer(
int _nOctaveLayers,
const std::vector<Mat>& _gpyr,
std::vector<Mat>& _dogpyr)
: nOctaveLayers(_nOctaveLayers),
gpyr(_gpyr),
dogpyr(_dogpyr) { }
void operator()(const cv::Range& range) const CV_OVERRIDE
{
CV_TRACE_FUNCTION();
const int begin = range.start;
const int end = range.end;
for (int a = begin; a < end; a++)
{
const int o = a / (nOctaveLayers + 2);//确定该图像属于哪个Octave
const int i = a % (nOctaveLayers + 2);//确定该图像属于Octave的第几层
const Mat& src1 = gpyr[o * (nOctaveLayers + 3) + i];
const Mat& src2 = gpyr[o * (nOctaveLayers + 3) + i + 1];
Mat& dst = dogpyr[o * (nOctaveLayers + 2) + i];
subtract(src2, src1, dst, noArray(), DataType<sift_wt>::type);//第i+1层减去第i层
}
}
private:
int nOctaveLayers;
const std::vector<Mat>& gpyr;
std::vector<Mat>& dogpyr;
};
void SIFT_Impl::buildDoGPyramid(const std::vector<Mat>& gpyr, std::vector<Mat>& dogpyr) const
{
CV_TRACE_FUNCTION();
int nOctaves = (int)gpyr.size() / (nOctaveLayers + 3);
dogpyr.resize(nOctaves * (nOctaveLayers + 2));//保存所有的DoG图像
// 并行计算，共nOctaves个Octave，每个Octave有nOctaveLayers+3层，共nOctaves * (nOctaveLayers + 2)个差分计算
parallel_for_(Range(0, nOctaves * (nOctaveLayers + 2)), buildDoGPyramidComputer(nOctaveLayers, gpyr, dogpyr));
}
1.2 找关键点
1.2.1 查找初始关键点
由高斯金字塔得到每组n+3层图像，所有相邻两幅高斯滤波图像得到n+2个差函数D(x,y,σ)。将这些差函数视为图像，图像的细节水平随着我们上调尺度空间而下降。下图显示了SIFT查找图像D(x,y,σ)中的极值的过程。
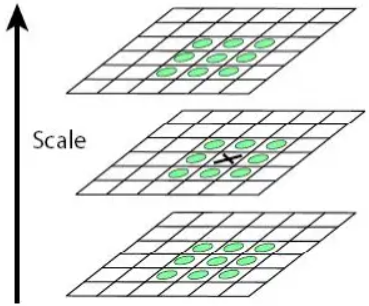
在D(x,y,σ)图像中的每个位置（显示为黑色x），将该位置的像素值与其在当前图像中的8个相邻像素值及其在上方和下方图像中的9个相邻像素值，即26个相邻像素，进行比较。如果该位置的值大于其所有相邻像素的值，或小于所有相邻像素的值，那么该位置被选为极值（最大值或最小值点）。在一个Octave的第一个（最后一个）尺度中检测不到任何极值，因为它没有相同大小的下方（上方）尺度图像。
OpenCV查找初始关键点源码
在DoG尺度空间中找初始极值点，是通过比较每一个像素与其26个邻域像素相比较。如果该位置的值大于其所有相邻像素的值，或小于所有相邻像素的值，那么该位置被选为极值。OpenCV中对应的是findScaleSpaceExtremaT类，其中包括了极值计算，调整极值，梯度计算等。下面为极值计算部分。
void process(const cv::Range& range)
{
CV_TRACE_FUNCTION();
const int begin = range.start;
const int end = range.end;
static const int n = SIFT_ORI_HIST_BINS;
float CV_DECL_ALIGNED(CV_SIMD_WIDTH) hist[n];
const Mat& img = dog_pyr[idx];
const Mat& prev = dog_pyr[idx - 1];
const Mat& next = dog_pyr[idx + 1];
for (int r = begin; r < end; r++)
{
const sift_wt* currptr = img.ptr<sift_wt>(r);
const sift_wt* prevptr = prev.ptr<sift_wt>(r);
const sift_wt* nextptr = next.ptr<sift_wt>(r);
int c = SIFT_IMG_BORDER;
// vector loop reminder, better predictibility and less branch density
for (; c < cols - SIFT_IMG_BORDER; c++)
{
sift_wt val = currptr[c];
if (std::abs(val) <= threshold)
continue;
sift_wt _00, _01, _02;
sift_wt _10, _12;
sift_wt _20, _21, _22;
_00 = currptr[c - step - 1]; _01 = currptr[c - step]; _02 = currptr[c - step + 1];
_10 = currptr[c - 1]; _12 = currptr[c + 1];
_20 = currptr[c + step - 1]; _21 = currptr[c + step]; _22 = currptr[c + step + 1];
bool calculate = false;
if (val > 0)//当val大于0，找极大值
{
sift_wt vmax = std::max(std::max(std::max(_00, _01), std::max(_02, _10)), std::max(std::max(_12, _20), std::max(_21, _22)));
if (val >= vmax)//当前点和8邻域相比是否为极大值
{
_00 = prevptr[c - step - 1]; _01 = prevptr[c - step]; _02 = prevptr[c - step + 1];
_10 = prevptr[c - 1]; _12 = prevptr[c + 1];
_20 = prevptr[c + step - 1]; _21 = prevptr[c + step]; _22 = prevptr[c + step + 1];
vmax = std::max(std::max(std::max(_00, _01), std::max(_02, _10)), std::max(std::max(_12, _20), std::max(_21, _22)));
if (val >= vmax)//当前点和上一层的8邻域相比是否为极大值
{
_00 = nextptr[c - step - 1]; _01 = nextptr[c - step]; _02 = nextptr[c - step + 1];
_10 = nextptr[c - 1]; _12 = nextptr[c + 1];
_20 = nextptr[c + step - 1]; _21 = nextptr[c + step]; _22 = nextptr[c + step + 1];
vmax = std::max(std::max(std::max(_00, _01), std::max(_02, _10)), std::max(std::max(_12, _20), std::max(_21, _22)));
if (val >= vmax)//当前点和下一层的8邻域相比是否为极大值
{
sift_wt _11p = prevptr[c], _11n = nextptr[c];
calculate = (val >= std::max(_11p, _11n));//当前点和上下两层对应点相比是否为极大值
}
}
}
}
else { // val cant be zero here (first abs took care of zero), must be negative// val要不是正的，要不是负的，不可能是0
sift_wt vmin = std::min(std::min(std::min(_00, _01), std::min(_02, _10)), std::min(std::min(_12, _20), std::min(_21, _22)));
if (val <= vmin)
{
_00 = prevptr[c - step - 1]; _01 = prevptr[c - step]; _02 = prevptr[c - step + 1];
_10 = prevptr[c - 1]; _12 = prevptr[c + 1];
_20 = prevptr[c + step - 1]; _21 = prevptr[c + step]; _22 = prevptr[c + step + 1];
vmin = std::min(std::min(std::min(_00, _01), std::min(_02, _10)), std::min(std::min(_12, _20), std::min(_21, _22)));
if (val <= vmin)
{
_00 = nextptr[c - step - 1]; _01 = nextptr[c - step]; _02 = nextptr[c - step + 1];
_10 = nextptr[c - 1]; _12 = nextptr[c + 1];
_20 = nextptr[c + step - 1]; _21 = nextptr[c + step]; _22 = nextptr[c + step + 1];
vmin = std::min(std::min(std::min(_00, _01), std::min(_02, _10)), std::min(std::min(_12, _20), std::min(_21, _22)));
if (val <= vmin)
{
sift_wt _11p = prevptr[c], _11n = nextptr[c];
calculate = (val <= std::min(_11p, _11n));
}
}
}
}
...//后面还有求亚像素精度极值，梯度方向直方图
}
1.2.2 改进关键点位置的精度
一个连续函数被取样时，它真正的最大值或最小值实际上可能位于样本点之间。得到接近真实极值（亚像素精度）的一种方法时，首先再数字函数中的每个极值点处拟合一个内插函数，然后在内插后的函数中查找改进精度后的极值位置。SIFT用D(x,y,σ)的泰勒级数展开的线性项和二次项，把原点移至被检测的样本点。这个公式的向量形式为
式中，D及其导数是在这个样本点处计算的，x=(x,y,σ)T是这个样本的偏移量，▽是我们熟悉的梯度算子，
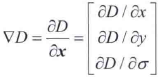
H是海森矩阵，
取D(x)关于x的导数并令其为零，可求得极值的位置x，即
就像在博客1.2节介绍的那样，海森矩阵和D的梯度是用相邻像素点的差来近似的，f'(x)=(f(x+1)-f(x-1))/2，二阶导数f''(x)=f(x+1)+f(x-1)-2f(x)。得到的3×3线性方程组加u三上很容易求解。如果偏移量x在其任意维度上都大于0.5，那么可以得出结论：极值靠近另一个样本点，在这种情况下，改变样本点，并对改变后的样本点进行内插。最后的偏移量x被添加到其样本点的位置，得到极值的内插后的估计位置。
SIFT使用极值位置函数值D(x)来剔除具有低对比度的不稳定极值，其中D(x)为
Lowe的实验结果称，若所有图像的值都在区间[0,1]内，则D(x)小于0.03的任何极值都会被剔除。这剔除了具有低对比度和/或局部化较差的关键点。
1.2.3 消除边缘响应
回顾边缘检测的博客可知，使用高斯差会得到图像中的边缘。但SIFT中我们感兴趣的关键点是“角状”特征，这些特征更加局部化。因此，消除了边缘导致的灰度过渡。为了量化边和角之间的差，我们研究局部曲折度。边在一个方向上由高曲折度表征，在正交方向上由低曲折度表征。图像中某点的曲折度可由该点处的一个2×2海森矩阵算出。因此，要在标量空间中的任何一层计算DoG的局部曲折度，可在该层中计算D的海森矩阵：
H的特征值与D的曲折度成正比。如对哈里斯-斯蒂芬斯(HS)角检测器的解释那样，我们可以避免直接计算特征值，H的迹等于特征值之和，H的行列式等于特征值之积。设α和β分别是H的最大特征值和最小特征值，有
注意，H是对称的，且大小为2×2。若行列式是负的，则不同曲折度具有不同的符号，且讨论的关键点不可能是一个极值，因此要丢弃它。令r表示最大特征值和最小特征值之比，即α=rβ，则
当特征值相等时，上式出现最小值，当r大于1时，随着r的增大而增大。因此，要检查低于某个阈值的r的主曲折度之比，只需检查
这个计算很简单。Lowe报告的实验结果中使用了值r=10，这意味着消除了曲折度之比大于10的关键点。
OpenCV源码adjustLocalExtrema
包括计算亚像素精度极值+剔除低对比度的不稳定极值+剔除曲折度较大的点，基于Lowe论文的Section 4
static bool adjustLocalExtrema(
const std::vector<Mat>& dog_pyr, KeyPoint& kpt, int octv,
int& layer, int& r, int& c, int nOctaveLayers,
float contrastThreshold, float edgeThreshold, float sigma
)
{
CV_TRACE_FUNCTION();
const float img_scale = 1.f / (255 * SIFT_FIXPT_SCALE);
const float deriv_scale = img_scale * 0.5f;
const float second_deriv_scale = img_scale;
const float cross_deriv_scale = img_scale * 0.25f;
float xi = 0, xr = 0, xc = 0, contr = 0;
int i = 0;
for (; i < SIFT_MAX_INTERP_STEPS; i++)
{
int idx = octv * (nOctaveLayers + 2) + layer;
const Mat& img = dog_pyr[idx];
const Mat& prev = dog_pyr[idx - 1];
const Mat& next = dog_pyr[idx + 1];
//D(x,y,σ)在样本点点的导数，用中心差分计算
Vec3f dD((img.at<sift_wt>(r, c + 1) - img.at<sift_wt>(r, c - 1)) * deriv_scale,
(img.at<sift_wt>(r + 1, c) - img.at<sift_wt>(r - 1, c)) * deriv_scale,
(next.at<sift_wt>(r, c) - prev.at<sift_wt>(r, c)) * deriv_scale);
// 基于中心差分的二阶导数
float v2 = (float)img.at<sift_wt>(r, c) * 2;
float dxx = (img.at<sift_wt>(r, c + 1) + img.at<sift_wt>(r, c - 1) - v2) * second_deriv_scale;
float dyy = (img.at<sift_wt>(r + 1, c) + img.at<sift_wt>(r - 1, c) - v2) * second_deriv_scale;
float dss = (next.at<sift_wt>(r, c) + prev.at<sift_wt>(r, c) - v2) * second_deriv_scale;
float dxy = (img.at<sift_wt>(r + 1, c + 1) - img.at<sift_wt>(r + 1, c - 1) -
img.at<sift_wt>(r - 1, c + 1) + img.at<sift_wt>(r - 1, c - 1)) * cross_deriv_scale;
float dxs = (next.at<sift_wt>(r, c + 1) - next.at<sift_wt>(r, c - 1) -
prev.at<sift_wt>(r, c + 1) + prev.at<sift_wt>(r, c - 1)) * cross_deriv_scale;
float dys = (next.at<sift_wt>(r + 1, c) - next.at<sift_wt>(r - 1, c) -
prev.at<sift_wt>(r + 1, c) + prev.at<sift_wt>(r - 1, c)) * cross_deriv_scale;
//海森矩阵
Matx33f H(dxx, dxy, dxs,
dxy, dyy, dys,
dxs, dys, dss);
//取D(X)关于X的导数并令其为零，可求得极值的位置X, X = (x, y, σ)T
//即，HX=-dD
Vec3f X = H.solve(dD, DECOMP_LU);
xi = -X[2];
xr = -X[1];
xc = -X[0];
//如果由泰勒级数插值得到的三个坐标的偏移量都小于0.5，说明已经找到特征点，则退出迭代
if (std::abs(xi) < 0.5f && std::abs(xr) < 0.5f && std::abs(xc) < 0.5f)
break;
//如果三个坐标偏移量中任意一个大于一个很大的数，则说明该极值点不是特征点，函数返回
if (std::abs(xi) > (float)(INT_MAX / 3) ||
std::abs(xr) > (float)(INT_MAX / 3) ||
std::abs(xc) > (float)(INT_MAX / 3))
return false;
//由上面得到的偏移量重新定义插值中心的坐标位置,用于下次迭代，上面偏移量小于0.5的话，四舍五入还在layer层的(r，c)点，就不用下面的几句
c += cvRound(xc);
r += cvRound(xr);
layer += cvRound(xi);
//如果新的坐标超出了金字塔的坐标范围，则说明该极值点不是特征点，函数返回
if (layer < 1 || layer > nOctaveLayers ||
c < SIFT_IMG_BORDER || c >= img.cols - SIFT_IMG_BORDER ||
r < SIFT_IMG_BORDER || r >= img.rows - SIFT_IMG_BORDER)
return false;
}
// ensure convergence of interpolation //如果迭代次数超过最大迭代次数，这个极值点不是特征点
if (i >= SIFT_MAX_INTERP_STEPS)
return false;
// 剔除具有低对比度的不稳定极值 D(X)=D+0.5*dD*X
{
int idx = octv * (nOctaveLayers + 2) + layer;
const Mat& img = dog_pyr[idx];
const Mat& prev = dog_pyr[idx - 1];
const Mat& next = dog_pyr[idx + 1];
Matx31f dD((img.at<sift_wt>(r, c + 1) - img.at<sift_wt>(r, c - 1)) * deriv_scale,
(img.at<sift_wt>(r + 1, c) - img.at<sift_wt>(r - 1, c)) * deriv_scale,
(next.at<sift_wt>(r, c) - prev.at<sift_wt>(r, c)) * deriv_scale);
float t = dD.dot(Matx31f(xc, xr, xi));
contr = img.at<sift_wt>(r, c) * img_scale + t * 0.5f;
if (std::abs(contr) * nOctaveLayers < contrastThreshold)//当响应值D(X)小于contrastThreshold时剔除
return false;
// 剔除曲折度较大的点，利用Hessian的迹和行列式计算曲折度，和上面不同，下面的Hessian是2×2的
// principal curvatures are computed using the trace and det of Hessian
float v2 = img.at<sift_wt>(r, c) * 2.f;
float dxx = (img.at<sift_wt>(r, c + 1) + img.at<sift_wt>(r, c - 1) - v2) * second_deriv_scale;
float dyy = (img.at<sift_wt>(r + 1, c) + img.at<sift_wt>(r - 1, c) - v2) * second_deriv_scale;
float dxy = (img.at<sift_wt>(r + 1, c + 1) - img.at<sift_wt>(r + 1, c - 1) -
img.at<sift_wt>(r - 1, c + 1) + img.at<sift_wt>(r - 1, c - 1)) * cross_deriv_scale;
float tr = dxx + dyy;
float det = dxx * dyy - dxy * dxy;
//若行列式是负的，则不同曲折度具有不同的符号，且讨论的关键点不可能是一个极值，因此要丢弃它。曲折度大就说明两个特征值相差大，就是边缘，丢弃
if (det <= 0 || tr * tr * edgeThreshold >= (edgeThreshold + 1) * (edgeThreshold + 1) * det)
return false;
}
//保存特征点信息
kpt.pt.x = (c + xc) * (1 << octv);
kpt.pt.y = (r + xr) * (1 << octv);
kpt.octave = octv + (layer << 8) + (cvRound((xi + 0.5) * 255) << 16);
kpt.size = sigma * powf(2.f, (layer + xi) / nOctaveLayers) * (1 << octv) * 2;
kpt.response = std::abs(contr);
return true;
}
1.3 计算关键点方向
在之前过程中，我们得到了SIFT认为稳定的关键点。因为我们知道每个关键点在尺度空间中的位置，因此实现了尺度独立性。下一步是根据局部性质为每个关键点分配方向，实现图像旋转的不变性。对此，SIFT使用了一种简单的方法：
- 使用关键点的尺度来选择最接近该尺度的高斯平滑图像L，然后采集关键点所在高斯金字塔图像3σ邻域窗口内像素的梯度幅度M(x,y)和方向角θ(x,y):
- 方向直方图由每个关键点邻域的样本点的梯度方向形成。直方图有36个容器，覆盖了图像平面上360°的方向范围（或者每45度一个柱共8个柱)。添加到直方图中的每个样本按其梯度幅度和一个圆形高斯函数加权（也就是说灰度差大的方向对关键点方向的影响更大，也增强特征点近的邻域点对关键点方向的作用，并减少突变的影响），圆形高斯函数的标准差是关键点尺度的1.5倍。
- 为了得到更精确的方向，通常还可以对离散的梯度直方图进行插值拟合。具体而言，关键点的方向可以由和主峰值最近的三个柱值通过抛物线插值得到。
- 在梯度直方图中，当存在一个相当于主峰值80%能量的柱值时，则可以在相同的位置以相同的尺度创建另一个关键点，关键点的方向不同。SIFT仅为15%左右的多方向点分配多个方向，但它们对图像匹配的贡献非常明显。
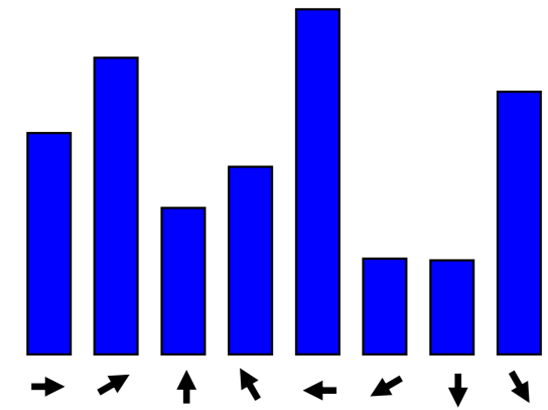
OpenCV源码calcOrientationHist
// Computes a gradient orientation histogram at a specified pixel
static float calcOrientationHist(
const Mat& img, Point pt, int radius,
float sigma, float* hist, int n
)
{
CV_TRACE_FUNCTION();
int i, j, k, len = (radius*2+1)*(radius*2+1);
float expf_scale = -1.f/(2.f * sigma * sigma);
cv::utils::BufferArea area;
float *X = 0, *Y = 0, *Mag, *Ori = 0, *W = 0, *temphist = 0;
area.allocate(X, len, CV_SIMD_WIDTH);
area.allocate(Y, len, CV_SIMD_WIDTH);
area.allocate(Ori, len, CV_SIMD_WIDTH);
area.allocate(W, len, CV_SIMD_WIDTH);
area.allocate(temphist, n+4, CV_SIMD_WIDTH);
area.commit();
temphist += 2;
Mag = X;
for( i = 0; i < n; i++ ) //初始化直方图
temphist[i] = 0.f;
for( i = -radius, k = 0; i <= radius; i++ )//两个for循环，计算(radius*2+1)*(radius*2+1)个dx，dy和w
{
int y = pt.y + i;
if( y <= 0 || y >= img.rows - 1 )
continue;
for( j = -radius; j <= radius; j++ )
{
int x = pt.x + j;
if( x <= 0 || x >= img.cols - 1 )
continue;
float dx = (float)(img.at<sift_wt>(y, x+1) - img.at<sift_wt>(y, x-1));//计算相对值，不用除以2了
float dy = (float)(img.at<sift_wt>(y-1, x) - img.at<sift_wt>(y+1, x));
X[k] = dx; Y[k] = dy; W[k] = (i*i + j*j)*expf_scale;//这里的W为高斯函数的e的指数
k++;
}
}
len = k;
// 计算邻域中所有元素的高斯加权值W，梯度幅角Ori 和梯度幅值Mag
// compute gradient values, orientations and the weights over the pixel neighborhood
cv::hal::exp32f(W, W, len);
cv::hal::fastAtan2(Y, X, Ori, len, true);
cv::hal::magnitude32f(X, Y, Mag, len);
k = 0;
for( ; k < len; k++ )//涨知识了，我每次都要写老长的判断，判断是在第几象限
{
int bin = cvRound((n/360.f)*Ori[k]);//判断邻域像素的梯度幅角属于n个柱体的哪一个，和Lowe推荐的方法不同，它选了最近的柱体，然后再平滑
//如果超出范围，则利用圆周循环确定其真正属于的那个柱体，比如dy=-1，dx=1，Ori=-45°，假设n=8，bin=-1，bin+=n，就是第7个柱体
if( bin >= n )
bin -= n;
if( bin < 0 )
bin += n;
temphist[bin] += W[k]*Mag[k];//直方图放入的值是带高斯加权的幅值，增强特征点近的邻域点对关键点方向的作用，并减少突变的影响
}
// smooth the histogram
temphist[-1] = temphist[n-1];//为了圆周循环，提前填充好直方图前后各两个变量
temphist[-2] = temphist[n-2];//公式不是要取前面两个和后面两个一起平滑嘛
temphist[n] = temphist[0];//也就是说，第一个应该取最后两个一起计算，所以把最后两个拷到前面去
temphist[n+1] = temphist[1];
// 平滑直方图
i = 0;
for( ; i < n; i++ )
{
hist[i] = (temphist[i-2] + temphist[i+2])*(1.f/16.f) +
(temphist[i-1] + temphist[i+1])*(4.f/16.f) +
temphist[i]*(6.f/16.f);
}
//计算直方图的主峰值
float maxval = hist[0];
for( i = 1; i < n; i++ )
maxval = std::max(maxval, hist[i]);
return maxval;
}
1.4 关键点描述
经过前面的步骤，已经为关键点分配了图像位置、尺度和方向，进而为这三个变量提供了不变性。下一步是为围绕每个明显不同的关键点的局部区域计算一个描述子，同时对尺度、方向、光照和图像视点的变化是尽可能不变的。基本思想是能用这些描述子来识别两幅或多幅图像中局部区域的匹配（相似性）。特征描述子的生成大致有三个步骤：
1. 校正旋转主方向，确保旋转不变性。为了保证特征矢量的旋转不变性，要以特征点为中心，在附近邻域内将坐标轴旋转θθ（特征点的主方向）角度，即将坐标轴旋转为特征点的主方向。旋转后邻域内像素的新坐标为：
2. 生成描述子，最终形成一个128维的特征向量。
以关键点为中心取16×16像素的一个区域，并使用像素差计算这个区域中每个点处的梯度幅度和方向。然后使用标准差等于这个区域大小一般的高斯加权函数来分配一个权重，将这个权重乘以每个点处的梯度幅度。高斯加权函数在图中显示为一个圆，权重随着到中心的距离增大而减小。这个函数的目的是，减少位置变化很小时描述子的突然变化。
将16×16的区域分为16个4×4区域，每个4×4区域中有16个方向，将所有的梯度方向量化为8个相隔45°的方向。SIFT不是把一个方向值分配给其最接近的容器，而是进行内插运算，根据这个值到每个容器中心的距离，按比例地在所有容器中分配直方图的输入。例如，容器的中心为[22.5, 67.5, 112.5, ..., 337.5]，每个输入需要乘以权重1-d，d是从这个值到容器中心的最短距离，度量单位是直方图间隔，最大的可能距离是1。假设某个方向值是22.5°，到第一个容器中心的距离是0，因此将满输入分配给这个容器。到下一个容器的距离是1，1-d=0，所以不分配给下一个容器，所有容器都是如此。假设某个方向值是45°，分配给第一个容器1/2，分配给第二个容器1/2。采用这种方法，为每个容器得到一个技术的比例分数，从而避免“边界”效应，即描述子方向的细微变化导致的为不同容器分配到同一个值的效应。
16个4×4区域得到16个直方图，将直方图的8个方向显示为一个小向量簇，其中每个向量的长度等于其对应容器的值。所以，一个描述子由4×4阵列组成，每个阵列包含8个方向值。在SIFT中，这描述子数据被组织为一个128维的向量。
3. 归一化处理，将特征向量长度进行归一化处理，进一步去除光照的影响。
为了降低光照的影响，对特征向量进行了两阶段的归一化处理。首先，通过将每个分量除以向量范数，把向量归一化为单位长度。由每个像素值乘以一个常数所引起的图像对比度的变化，将以相同的常数乘以梯度，因此对比度的变化将被第一次归一化抵消。每个像素加上一个常量导致的亮度变化不会影响梯度值，因为梯度值是根据像素插值计算的。因此描述子对光照的仿射变换是不变的。然后，也可能出现摄像机饱和等导致的非线性光照变化。这类变化会导致某些梯度的相对幅值的较大变化，但它们几乎不会影响梯度方向。SIFT通过对归一化特征向量进行阈值处理，降低了较大梯度值的影响，使所有分量都小于实验确定的值0.2。阈值处理后，特征向量被重新归一化为单位向量。
2 opencv中的SIFT
2.1 SIFT使用示例
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
int main() {
Mat src1 = imread("./1.jpg", 0);
Mat src2 = imread("./2.jpg", 0);
Mat img1 = imread("./2.jpg");
Mat img2 = imread("./2.jpg");
SIFT S;
Ptr<SIFT> pSIFT = SIFT::create(55);
vector<KeyPoint> points1, points2;
pSIFT->detect(src1, points1);
pSIFT->detect(src2, points2);
drawKeypoints(src1, points1, img1, Scalar(0,255,0));
drawKeypoints(src2, points2, img2, Scalar(0, 255, 0));
Mat discriptions1, discriptions2;
pSIFT->compute(src1, points1, discriptions1);
pSIFT->compute(src2, points2, discriptions2);
Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create("BruteForce");
vector<DMatch> matches;
matcher->match(discriptions1, discriptions2, matches);
Mat match_img;
drawMatches(src1, points1, src2, points2, matches, match_img);
imshow("markImg", match_img);
waitKey(0);
return 0;
}
2.2 源码分析
SIFT构造函数，查询用户是否提供关键点，然后调用以下函数
- 建立初始图像SIFT::createInitialImage()
- 建立高斯金字塔SIFT::buildGaussianPyramid()√
- 建立DoG金字塔 SIFT::buildDoGPyramid()√
- 在DoG中查找尺度空间极值点SIFT::findScaleSpaceExtrema()√，会调用下面两个函数
（1）对找到的极值点进行曲线插值拟合，并过滤 adjustLocalExtrema()√
（2）计算方向直方图 calcOrientationHist()√
- 计算描述子 calcDescriptors()
（1）计算sift描述子calcSIFTDescriptor()
上面在讲原理的时候已经写了一些源码注释（打√），下面是剩下的注释。
2.2.1 SIFT::createInitialImage()
其中σinit是第0层的尺度，σpre是被相机模糊后的尺度。在Lowe的论文使用了σ0=1.6，S=3。
为了尽可能多的保留原始图像信息，一般需要对原始图像进行扩大两倍采样，即升采样，从而生成一组采样图octave_1,此组采样图的第一层的模糊参数为：
也就是说，输入的图像已经是被模糊了（0.5），但你想要更模糊一点（1.6）的作为base。如果要先扩大图像尺寸的话，就先升采样后再用1.25的σ进行卷积。如果不升采样的话，就用sqrt(1.6*1.6-0.5*0.5)对原图做卷积，然后将结果作为base。
static Mat createInitialImage( const Mat& img, bool doubleImageSize, float sigma )
{
Mat gray, gray_fpt;
if( img.channels() == 3 || img.channels() == 4 )
{ //如果输入图像是彩色图像，则需要转换成灰度图像
cvtColor(img, gray, COLOR_BGR2GRAY);
gray.convertTo(gray_fpt, DataType<sift_wt>::type, SIFT_FIXPT_SCALE, 0);//调整图像的像素数据类型
}
else
img.convertTo(gray_fpt, DataType<sift_wt>::type, SIFT_FIXPT_SCALE, 0);
float sig_diff;
if( doubleImageSize )//如果需要扩大图像的长宽尺寸
{
//SIFT_INIT_SIGMA为0.5，即输入图像的尺度，SIFT_INIT_SIGMA×2 = 1.0，即图像扩大2倍以后的尺度
sig_diff = sqrtf( std::max(sigma * sigma - SIFT_INIT_SIGMA * SIFT_INIT_SIGMA * 4, 0.01f) );
Mat dbl;
#if DoG_TYPE_SHORT
resize(gray_fpt, dbl, Size(gray_fpt.cols*2, gray_fpt.rows*2), 0, 0, INTER_LINEAR_EXACT);
#else
resize(gray_fpt, dbl, Size(gray_fpt.cols*2, gray_fpt.rows*2), 0, 0, INTER_LINEAR);//利用双线性插值法把图像的长宽都扩大2倍
#endif
Mat result;
GaussianBlur(dbl, result, Size(), sig_diff, sig_diff);//对图像进行高斯平滑处理
return result;
}
else//如果不需要扩大图像的尺寸，sig_diff计算不同
{
sig_diff = sqrtf( std::max(sigma * sigma - SIFT_INIT_SIGMA * SIFT_INIT_SIGMA, 0.01f) );
Mat result;
GaussianBlur(gray_fpt, result, Size(), sig_diff, sig_diff);
return result;
}
}
1. 计算邻域内每个像素点的幅值和幅角
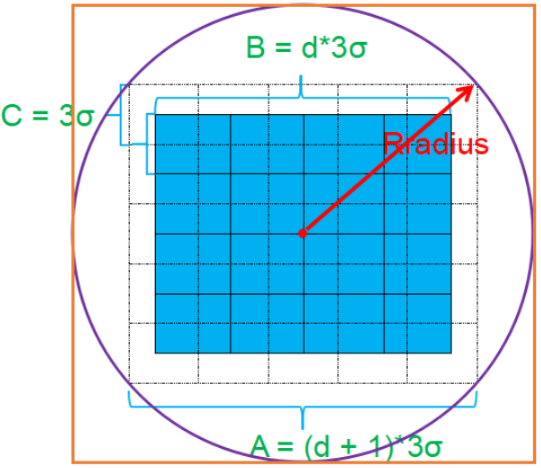
在前面的步骤中我们分别得到了关键点的位置（层，组，所在图像的横纵坐标），尺度，主方向信息。所以我们定位关键点到其所属的高斯金字塔中的那幅图中。用关键点周围(radius*2+1)*(radius*2+1)的邻域（橘色矩形框区域）来描述这个关键点，即计算邻域的幅值和幅角，其中
将这块区域分成d×d个小区域，SIFT中d取4，每个小区域的宽度是3σ，这里的σ是指相对于当前组第一层图片来说的。
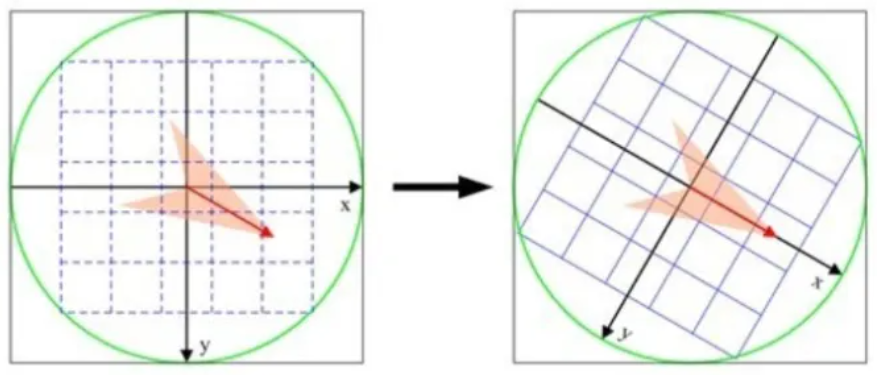
2. 校正旋转主方向，确保旋转不变性。
为了保证特征矢量的旋转不变性，要以特征点为中心，在附近邻域内将坐标轴旋转θ（特征点的主方向）角度，即将坐标轴旋转为特征点的主方向。如下图所示
旋转后邻域内像素的新坐标为：
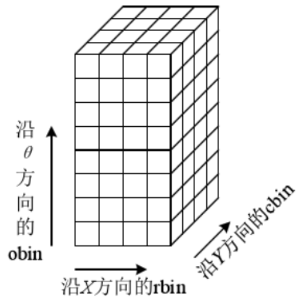
3.建立三维直方图
在计算特征点描述符的时候，我们不需要精确知道邻域内所有像素的梯度幅值和幅角，我们只需要根据直方图知道其统计值即可。如图所示，三维直方图是由d*d*n个长宽为1的单位立方体组成的，高对应邻域像素幅角的大小，把360度分成8等分。立方体的底就是特征点的邻域区域，该区域被划分为4×4个子区域，邻域中的像素根据坐标位置，把它们归属到这16个子区域中的一个，再根据该像素幅角的大小，把它分到这8等分中的一份，这样每个像素点都能对应到其中的一个立方体内，三维直方图建立起来了。
正方体的中心代表着该正方体，但是落入正方体内的邻域像素不可能都在中心，因此我们需要对上面的梯度幅值做进一步的处理，根据它对中心点位置的贡献大小进行加权处理，即在正方体内，根据像素点相对于正方体中心的距离，对梯度幅值做加权处理。所以，三维直方图的值，也就是正方体的值需要下面四个步骤完成：
1）计算落入该正方体内的邻域像素的梯度幅值A
2）根据该像素相对于特征点的距离，对A进行高斯加权处理，得到B
3）根据该像素相对于它所在的正方体的中心的贡献大小，再对B进行加权处理，得到C
由于计算相对于正方体中心点的贡献大小略显繁琐,例如像素（0.25,0.25,0.25），中心点为（0.5,0.5,0.5），相对距离是（0.25,0.25,0.25），贡献权重为(1-0.25)*(1-0.25)*(1-0.25)。因此在实际应用中，我们需要经过坐标平移，把中心点平移到正方体的顶点上,这样只要计算正方体内的点对正方体的8个顶点的贡献即可。根据三线性插值法，对某个顶点的贡献值是以该顶点和正方体内的点为对角线的两个顶点，所构成的立方体的体积。也就是对8个顶点的贡献分别为：
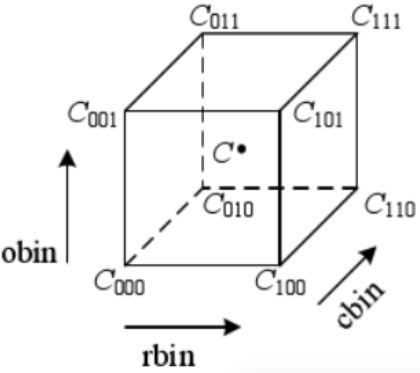
经过上述处理后我们得到128维描述子，在OpenCV中，一共对描述子进行了两次归一化处理。第一次使用以下公式对描述子进行归一化处理，并对大于0.2的描述子进行截断处理：
假设经过第一次归一化后描述子用qi表示，第二次归一化操作是
其中分母要大于FLT_EPSILON。
void calcSIFTDescriptor(
const Mat& img, Point2f ptf, float ori, float scl,
int d, int n, Mat& dstMat, int row
)
{
Point pt(cvRound(ptf.x), cvRound(ptf.y));//特征点坐标位置
float cos_t = cosf(ori*(float)(CV_PI/180));//特征点方向的余弦
float sin_t = sinf(ori*(float)(CV_PI/180));//特征点方向的正弦
float bins_per_rad = n / 360.f;// 1/45
float exp_scale = -1.f/(d * d * 0.5f); //高斯加权函数中的e指数的常数部分
float hist_width = SIFT_DESCR_SCL_FCTR * scl;//SIFT_DESCR_SCL_FCTR = 3.f，即3σ
int radius = cvRound(hist_width * 1.4142135623730951f * (d + 1) * 0.5f);//特征点邻域区域的半径
// Clip the radius to the diagonal of the image to avoid autobuffer too large exception
radius = std::min(radius, (int)std::sqrt(((double) img.cols)*img.cols + ((double) img.rows)*img.rows));//避免邻域过大
cos_t /= hist_width;//归一化处理
sin_t /= hist_width;
//len为特征点邻域区域内像素的数量，histlen为直方图的数量，即特征矢量的长度，实际应为d×d×n，+2是为圆周循环留出一定的内存空间
int i, j, k, len = (radius*2+1)*(radius*2+1), histlen = (d+2)*(d+2)*(n+2);
int rows = img.rows, cols = img.cols;
//开辟一段内存空间
cv::utils::BufferArea area;
float *X = 0, *Y = 0, *Mag, *Ori = 0, *W = 0, *RBin = 0, *CBin = 0, *hist = 0, *rawDst = 0;
area.allocate(X, len, CV_SIMD_WIDTH);
area.allocate(Y, len, CV_SIMD_WIDTH);
area.allocate(Ori, len, CV_SIMD_WIDTH);
area.allocate(W, len, CV_SIMD_WIDTH);
area.allocate(RBin, len, CV_SIMD_WIDTH);
area.allocate(CBin, len, CV_SIMD_WIDTH);
area.allocate(hist, histlen, CV_SIMD_WIDTH);
area.allocate(rawDst, len, CV_SIMD_WIDTH);
area.commit();
Mag = Y;
//直方图数组hist清零
for( i = 0; i < d+2; i++ )
{
for( j = 0; j < d+2; j++ )
for( k = 0; k < n+2; k++ )
hist[(i*(d+2) + j)*(n+2) + k] = 0.;
}
//遍历当前特征点的邻域范围
for( i = -radius, k = 0; i <= radius; i++ )
for( j = -radius; j <= radius; j++ )
{
// Calculate sample's histogram array coords rotated relative to ori.
// Subtract 0.5 so samples that fall e.g. in the center of row 1 (i.e.
// r_rot = 1.5) have full weight placed in row 1 after interpolation.
//计算旋转后的位置坐标
float c_rot = j * cos_t - i * sin_t;
float r_rot = j * sin_t + i * cos_t;
//把邻域区域的原点从中心位置移到该区域的左下角，以便后面的使用。因为变量cos_t 和sin_t 都已
//进行了归一化处理，所以原点位移时只需要加d/2即可。而再减0.5f的目的是进行坐标平移，从而在
//三线性插值计算中，计算的是正方体内的点对正方体8个顶点的贡献大小，而不是对正方体的中心点的
//贡献大小。之所以没有对角度obin 进行坐标平移，是因为角度是连续的量，无需平移
float rbin = r_rot + d/2 - 0.5f;
float cbin = c_rot + d/2 - 0.5f;
int r = pt.y + i, c = pt.x + j;//得到邻域像素点的位置坐标
//确定邻域像素是否在d×d 的正方形内，以及是否超过了图像边界
if( rbin > -1 && rbin < d && cbin > -1 && cbin < d &&
r > 0 && r < rows - 1 && c > 0 && c < cols - 1 )
{
//计算x和y方向的一阶导数，这里没有除以2，因为没有分母部分不影响后面所进行的归一化处理
float dx = (float)(img.at<sift_wt>(r, c+1) - img.at<sift_wt>(r, c-1));
float dy = (float)(img.at<sift_wt>(r-1, c) - img.at<sift_wt>(r+1, c));
X[k] = dx; Y[k] = dy; RBin[k] = rbin; CBin[k] = cbin;
W[k] = (c_rot * c_rot + r_rot * r_rot)*exp_scale;//高斯加权函数中的e 指数部分
k++;//统计实际的邻域像素的数量
}
}
len = k;
cv::hal::fastAtan2(Y, X, Ori, len, true);//计算梯度幅角
cv::hal::magnitude32f(X, Y, Mag, len);//计算梯度幅值
cv::hal::exp32f(W, W, len);//计算高斯加权函数
k = 0;
for( ; k < len; k++ )
{
float rbin = RBin[k], cbin = CBin[k];//得到d×d 邻域区域的坐标，即三维直方图的底内的位置
float obin = (Ori[k] - ori)*bins_per_rad;//得到幅角所属的8等份中的某一个等份，即三维直方图的高的位置
float mag = Mag[k]*W[k];//得到高斯加权以后的梯度幅值
//r0，c0和o0 为三维坐标的整数部分，它表示属于的哪个正方体
int r0 = cvFloor( rbin );//向下取整
int c0 = cvFloor( cbin );
int o0 = cvFloor( obin );
//rbin，cbin和obin 为三维坐标的小数部分，即将中心点移动到正方体端点时C点在正方体内的坐标
rbin -= r0;
cbin -= c0;
obin -= o0;
//如果角度o0 小于0 度或大于360 度，则根据圆周循环，把该角度调整到0～360度之间
if( o0 < 0 )
o0 += n;
if( o0 >= n )
o0 -= n;
// histogram update using tri-linear interpolation
//根据三线性插值法，计算该像素对正方体的8个顶点的贡献大小，即8个立方体的体积，这里还需要乘以高斯加权后的梯度值mag
float v_r1 = mag*rbin, v_r0 = mag - v_r1;
float v_rc11 = v_r1*cbin, v_rc10 = v_r1 - v_rc11;
float v_rc01 = v_r0*cbin, v_rc00 = v_r0 - v_rc01;
float v_rco111 = v_rc11*obin, v_rco110 = v_rc11 - v_rco111;
float v_rco101 = v_rc10*obin, v_rco100 = v_rc10 - v_rco101;
float v_rco011 = v_rc01*obin, v_rco010 = v_rc01 - v_rco011;
float v_rco001 = v_rc00*obin, v_rco000 = v_rc00 - v_rco001;
//得到该像素点在三维直方图中的索引
int idx = ((r0+1)*(d+2) + c0+1)*(n+2) + o0;
//8个顶点对应于坐标平移前的8个直方图的正方体，对其进行累加求和
hist[idx] += v_rco000;
hist[idx+1] += v_rco001;
hist[idx+(n+2)] += v_rco010;
hist[idx+(n+3)] += v_rco011;
hist[idx+(d+2)*(n+2)] += v_rco100;
hist[idx+(d+2)*(n+2)+1] += v_rco101;
hist[idx+(d+3)*(n+2)] += v_rco110;
hist[idx+(d+3)*(n+2)+1] += v_rco111;
}
// finalize histogram, since the orientation histograms are circular
//由于圆周循环的特性，纵向的n+2个正方体，使得第n个和第n+1个的值加到第0个和第1个上，而底部的（d+2）*（d+2）则是舍弃多出来的2
for( i = 0; i < d; i++ )
for( j = 0; j < d; j++ )
{
int idx = ((i+1)*(d+2) + (j+1))*(n+2);
hist[idx] += hist[idx+n];
hist[idx+1] += hist[idx+n+1];
for( k = 0; k < n; k++ )
rawDst[(i*d + j)*n + k] = hist[idx+k];
}
// copy histogram to the descriptor,
// apply hysteresis thresholding
// and scale the result, so that it can be easily converted
// to byte array
float nrm2 = 0;
len = d*d*n;
k = 0;
for( ; k < len; k++ )
nrm2 += rawDst[k]*rawDst[k];//将所有特征矢量的平方和累加起来
float thr = std::sqrt(nrm2)*SIFT_DESCR_MAG_THR;//累加平方和*0.2为阈值
i = 0, nrm2 = 0;
for( ; i < len; i++ )
{
float val = std::min(rawDst[i], thr);//大于阈值的值用thr代替
rawDst[i] = val;
nrm2 += val*val;
}
nrm2 = SIFT_INT_DESCR_FCTR/std::max(std::sqrt(nrm2), FLT_EPSILON);//截断后的用于归一化的值
k = 0;
if( dstMat.type() == CV_32F )
{
float* dst = dstMat.ptr<float>(row);
for( ; k < len; k++ )
{
dst[k] = saturate_cast<uchar>(rawDst[k]*nrm2);//归一化
}
}
else // CV_8U
{
uint8_t* dst = dstMat.ptr<uint8_t>(row);
for( ; k < len; k++ )
{
dst[k] = saturate_cast<uchar>(rawDst[k]*nrm2);
}
}
}
参考
1. 冈萨雷斯《数字图像处理（第四版）》Chapter 11（所有图片可在链接中下载）
2. 图像处理基础（六）基于 LOG 的 blob 兴趣点检测
4. 图像处理基础 （四）边缘提取之 LOG 和 DOG 算子
6. sift程序详解
