【图像处理笔记】特征提取之整体图像特征(Harris角点，MSER)

0 引言

特征提取之边界特征和特征提取之区域特征两篇博客介绍的描述子非常适合于某些应用（如工业检测），在这些应用中，可以使用图像分割中的方法可靠地分割图像中的各个区域。主分量特征向量与前面的内容是不同的，因为它们基于多幅图像。在某些应用中，如搜索图像数据库寻找匹配（如人脸识别），图像之间的变化非常广泛，因此这些方法都不再适用。本节将讨论两种解决这一问题的特征检测方法：（1）基于角的检测（2）处理图像中的所有区域。

1 哈里斯-斯蒂芬斯角检测器

1.1 原理及实现

我们直观的认为角是曲线方向的快速变化。角是高度有效的特征，因为它们对视点是独特且合理不变的。由于这些特性，角在诸如自动导航跟踪、立体机器视觉算法和图像数据库查询等应用中频繁用于匹配图像特征。

最常用的角点定义时Harris提出的，这些角点被称为“哈尔角点”，可以被认为是原始的关键点。它们的定义依赖于一个区域中的像素的自相关概念。简单来说，这意味着“如果图像被移动了少量(Δx,Δy)位置，它与原来的自己有多相似？”

哈尔从以下自相关函数开始计算，令f表示图像，并令f(s,t)表示由(s,t)的值定义的一小块图像。尺寸相同但移动了(x,y)的小块图像是f(s+x,t+y)。于是，两幅小块图像的差的平方的加权和为

式中，w(s,t)是一个后面很快就要讨论的加权函数。位移后的小块图像可以用泰勒级数展开的线性项来近似：

式中，fx(s,t)=df/dx和fy(s,t)=df/dy，它们都在(s,t)处计算。于是，上式可写为

用矩阵形式可写为

式中，

矩阵M是自相关矩阵。它的各项是在(s,t)处计算的。如果w(s,t)是各向同性的，那么M是对称的，因为A是对称的。在HS检测器中使用的加权函数w(s,t)通常有两种形式：（1）在小块图像内为1，在其他位置为0（即它的形状类似盒式低通滤波器核）；（2）指数形式，高斯加权，使靠近窗口中心的平方差比里中心更远的平方差的权重更大。当计算速度很快且噪音电平较低时，使用盒式核；数据平滑很重要时，使用指数函数。根据哈尔的定义，角点是图像中的自相关矩阵具有两个大的特征值的位置。实质上，这意味着在任何方向移动一小段距离都会造成图像改变。

哈里斯-斯蒂芬斯(HS)角检测器在图像上方移动一个小窗来检测灰度变化，像空间滤波那样。我们感兴趣的是三个场景，

（1）各个方向上零（或小）灰度变化的区域，这发生在检测器窗位于一个恒定（或几乎恒定）区域时，如位置A所示；

（2）在某个方向上变化但在其正交方向上不变化的区域，这发生在检测器窗口横跨两个区域之间的边界时，如位置B所示；

（3）所有方向发生重大变化的区域，这发生在检测器窗口包含一个角（或孤立点）时，如位置C所示。HS角检测器是试图区分这三个条件的数学公式。

实对称矩阵（如M）的特征向量指向最大的数据拓展方向，且对应的特征值与特征向量方向上的数据拓展成正比。事实上，特征向量是拟合数据的一个椭圆的主轴，特征值的幅度是从这个椭圆的中心到椭圆与主轴的交点的距离。该算法具有旋转不变性，但当图像被放大后，使用同样的窗口，就检测不到角点了，因此该算法不具有尺度不变性。下面说明如何使用这些性质来区分我们感兴趣的三种情况。

1. 求导：使用导数核w_y=[-1 0 1]和w_x=w_y^T计算(f_x,f_y)值。

2. 导数聚类：由于在小块图像中的每个点处计算导数时，噪声引起的变化会产生分散值，而分散的扩展与噪声水平及其性质直接相关。

平坦区域的导数形成了一个近似为圆形的聚类，其特征值几乎相同，产生了对这些点的一个近乎圆形的拟合。
包含边缘的小块图像的导数，沿x轴的扩展更大，沿y轴的扩展和平坦区域的几乎相同。于是两个特征值一个大一个小。拟合数据的椭圆在x方向拉长了。
包含角的小块图像的导数数据沿两个方向扩展，得到两个大特征值和一个大得多的几乎为圆形的拟合椭圆。

因此得出结论：（1）两个小特征值表示几乎恒定的灰度；（2）一个小特征值和一个大特征值表示存在垂直边界或水平边界；（3）两个大特征值表示存在一个角或孤立的亮点。因此我们可以用小块图像中由导数形成的矩阵的特征值来区分三种感兴趣的场景。

3. 角响应测度：由于特征值计算开销大，HS检测器使用了角响应测度。我们知道，一个平方矩阵的积等于该矩阵的特征值之和，该矩阵的行列式等于其特征值的积，角响应测度就是基于此，定义为

式中，k是一个常数，根据经验确定，默认为0.04。可以将k是为一个敏感因子，k越小，检测器越有可能找到角。当两个特征值都较大时，测度R具有较大正值，这表示存在一个角；一个特征值较大而另一个特征值较小时，测度R具有较小的负值；两个特征值都较小时，测度R的绝对值较小，表明小块图像时平坦的。R通常结合一个阈值T使用。当小块图像的R>T那么在小块图像中检测到了一个角。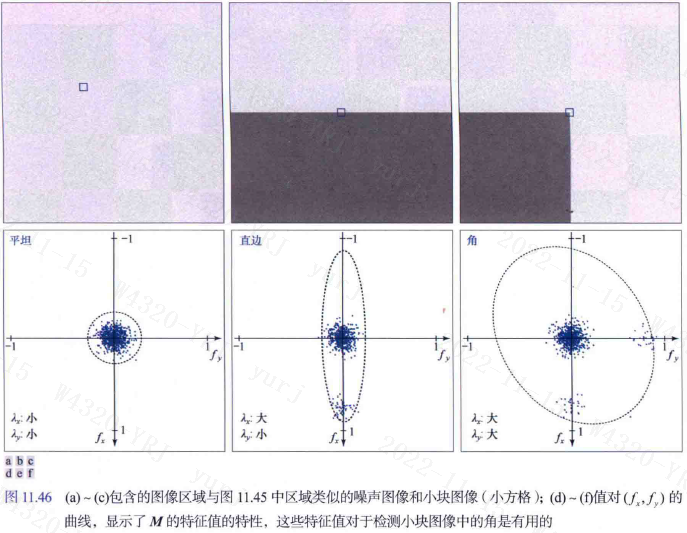

示例算法实现

#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
int main() {
    Mat src = imread("./12.bmp", 0);
    Mat markImg = imread("./12.bmp");
    Mat kx = (Mat_<float>(1, 3) << -1, 0, 1);
    Mat ky = (Mat_<float>(3, 1) << -1, 0, 1);
    vector<Rect> rects = { Rect(2225,350,30,30), Rect(2225,405,30,30), Rect(2190,405,30,30) };

    for (int i = 0; i < rects.size(); i++) {
        rectangle(markImg, rects[i], Scalar(0, 255, 0), 1);
        Mat roi = src(rects[i]);//从一张图上裁的三个区域
        Mat mask = Mat::zeros(Size(500, 500), CV_8UC1);
        Mat fx, fy;
        filter2D(roi, fx, CV_32F, kx);
        filter2D(roi, fy, CV_32F, ky);
        vector<Point> points;
        for (int i = 0; i < 30; i++) {
            for (int j = 0; j < 30; j++) {
                Point p = Point(fx.at<float>(i, j), fy.at<float>(i, j));
                Point p_offset = p + Point(250, 250);
                mask.at<uchar>(p_offset.y, p_offset.x) = 255;
                points.push_back(p_offset);
            }
        }
        Mat M = Mat::zeros(Size(2, 2), CV_32FC1);
        fx /= Scalar::all(255);
        fy /= Scalar::all(255);
        Mat q1, q2, q3;
        multiply(fx, fx, q1);
        multiply(fx, fy, q2);
        multiply(fy, fy, q3);
        M.at<float>(0, 0) = sum(sum(q1))[0];
        M.at<float>(0, 1) = sum(sum(q2))[0];
        M.at<float>(1, 0) = sum(sum(q2))[0];
        M.at<float>(1, 1) = sum(sum(q3))[0];

        Mat values;
        eigen(M, values);
        cout << "lamda1:" << values.ptr<float>(0)[0] << ", lamda2:" << values.ptr<float>(1)[0];
        double R = determinant(M) - 0.04 * pow(trace(M)[0], 2);
        cout << ", R:" << R << endl;
        imshow("roi"+to_string(i), roi);
        imshow("mask" + to_string(i), mask);
    }
    waitKey(0);
    return 0;
}

1.2 OpenCV中的Harris角检测器

OpenCV 中提供了 Harris 角点检测函数cv::cornerHarris()。

void cornerHarris( InputArray src, //输入图像，单通道的8位图像或浮点数图像
                   OutputArray dst, //输出图像，Harris检测器的响应，大小与src相同，格式为CV_32FC1
int blockSize,//邻域尺寸
                   int ksize, //Sobel算子的核大小
                   double k,//Harris检测器调节参数，通常取0.04-0.06
                   int borderType = BORDER_DEFAULT );//边界扩充类型

OpenCV函数cv::cornerSubPix()用于细化角点位置，以亚像素精度检测到角点位置.不仅可以用于对 Harris 角点检测结果进行细化检测，也可以用于对其它角点检测结果进行细化检测。

void cornerSubPix( InputArray image, 
                   InputOutputArray corners,
                   Size winSize,  
                   Size zeroZone,
                   TermCriteria criteria );

示例标定板找角点

下面的标定板过渡像素比较多，我们先找到Harris角，然后通过角（一些像素）的中心来细化它们。

#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;

int main() {
    Mat src = imread("./13.bmp", 0);
    Mat markImg = imread("./13.bmp");
    imshow("src", markImg);
    Mat dst, binImg;
    cornerHarris(src, dst, 5, 9, 0.04);
    normalize(dst, dst, 0, 1.0, NORM_MINMAX);
    threshold(dst, binImg, 0.25, 1, THRESH_BINARY);
    binImg.convertTo(binImg, CV_8U, 255);
    vector<vector<Point>> contours;
    findContours(binImg, contours, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE);
    vector<Point2f> corners;
    for (size_t i = 0; i < contours.size(); i++)
    {
        Point2f center; float radius;
        minEnclosingCircle(contours[i], center, radius);
        if(radius>2)
            corners.push_back(center);
    }
    TermCriteria criteria = TermCriteria(TermCriteria::EPS + TermCriteria::MAX_ITER, 1000, 0.001);
    cornerSubPix(src, corners, cv::Size(7, 7), cv::Size(-1, -1), criteria);
    for (size_t i = 0; i < corners.size(); i++)
        circle(markImg, corners[i], 3, Scalar(0, 255, 0), 3);
    imshow("markImg", markImg);
    waitKey(0);
    return 0;
}

2 最大稳定极值区域（MSER)

2.1 原理

　　上节讨论的哈里斯-斯蒂芬斯(HS)角检测器在由灰度的急剧过渡（如直边缘的交点，它在图像中会导致类似角的特征）表征的应用中是有用的。相反，Matas et al.[2002]提出的最大稳定极值区域（MSER）面向的更多的是“斑点”。像HS角检测器那样，MSER通常会产生整体图像特征，以便在两幅或多幅图像之间建立对应关系。

　　MSER算法是主要是基于分水岭的思想进行检测，其过程是：对一幅灰度图像取不同的阈值进行二值化处理，阈值从0至255递增，这个递增的过程就好比是一片土地上的水面不断上升，随着水位的不断上升，一些较低的区域就会逐渐被淹没，从天空鸟瞰，大地变为陆地、水域两部分，并且水域部分在不断扩大。在这个“漫水”的过程中，图像中的某些连通区域变化很小，甚至没有变化，则该区域就被称为最大稳定极值区域。

　　上面的过程可以转换为有根的连通树，它成为分量数。这棵树的每个节点表示一个极值区域，分析分量数的节点可以求出MSER。对于树中的每个连通区域，我们计算一个稳定性测度，定义为

式中，|R|是连通区域R的面积（像素数量），T是值域T∈[min(I), max(I)]内的一个阈值，ΔT是一个规定的阈值增量Ri，Rj，R是不同阈值得到的连通区域。MSER是分量数中的一个节点区域，该节点在该路径上具有局部极小的一个稳定值。可能有点难以理解，举个栗子，下面的图像灰度区间为[5,225]，取阈值T=10，ΔT=50对图像的不同区域进行分割。左边一列是阈值处理后的结果，右边是分量数。注意，数的根朝上。下图只有一个MSER。

2.2 OpenCV中的MSER

cv::MSER类的实例可以通过create方法创建。在初始化时指定被检测区域的最小和最大尺寸，以便限制被检测特征的数量。

Ptr<MSER> create( int delta=5, //允许灰度阈值的最小变化步长，即一次灰度值增加的量，取值范围（0,160），默认为5
                  int min_area=60, //允许区域最小的面积
                  int max_area=14400,//允许区域最大的面积
                  double max_variation=0.25, //允许不同强度阈值下的区域之间的最大面积变化率，取值范围为(0,1)，越接近1，则越多区域被认为是稳定的，如果接近0，则只能找到非常少的稳定区域，默认为0.25
                  double min_diversity=.2,//对于彩色图像，回溯以切断多样性小于 min_diversity 的 mser
                  int max_evolution=200, //对于彩色图像，进化步骤
                  double area_threshold=1.01,//对于彩色图像，导致重新初始化的区域阈值
                  double min_margin=0.003, //对于彩色图像，忽略太小的边距
                  int edge_blur_size=5 );//对于彩色图像，边缘模糊的光圈大小

可以通过调用 detectRegions 方法来获得 MSER，指定输入图像和一个相关的输出数据结构

void detectRegions( InputArray image,//输入图像可以是灰度图或者灰度图的梯度图
                    std::vector<std::vector<Point> >& msers,//mser区域用点表示
                    std::vector<Rect>& bboxes ) = 0;//mser区域用rect表示

示例利用MSER提取文字区域

　　书上的例子有点抽象，我搜了下，MSER在传统OCR中应用较广，是一个较为流行的文字检测传统方法（相对于基于深度学习的AI文字检测而言）。在一幅有文字的图像上，文字区域由于颜色（灰度值）是一致的，因此在水平面（阈值）持续增长的过程中，一开始不会被“淹没”，直到阈值增加到文字本身的灰度值时才会被“淹没”。该算法可以用来粗略地定位出图像中的文字区域位置。我找了张图试了下，效果不错，但是那张图直接做阈值分割+查找轮廓也能得到一样的效果。所以我又找了一张车牌，唔，有点东西。

#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;

bool cmp(Rect r1, Rect r2) {
    return r1.x < r2.x;
}
float IOU(const Rect& box1, const Rect& box2)
{
    if (box1.x > box2.x + box2.width) { return 0.0; }
    if (box1.y > box2.y + box2.height) { return 0.0; }
    if (box1.x + box1.width < box2.x) { return 0.0; }
    if (box1.y + box1.height < box2.y) { return 0.0; }
    float colInt = min(box1.x + box1.width, box2.x + box2.width) - max(box1.x, box2.x);
    float rowInt = min(box1.y + box1.height, box2.y + box2.height) - max(box1.y, box2.y);
    float intersection = colInt * rowInt;
    float area1 = box1.width * box1.height;
    float area2 = box2.width * box2.height;
    return intersection / (area1 + area2 - intersection);
}

vector<Rect> nms(vector<Rect> boxes, double overlapThreshold) {
    sort(boxes.begin(), boxes.end(), cmp); //将矩形框排序
    Rect r = boxes[0];
    vector<Rect> boxes_selectes = { r };
    int i = 1;
    while (i < boxes.size()) {
        if (!(IOU(r, boxes[i]) > overlapThreshold)) {//计算交并比
            boxes_selectes.push_back(boxes[i]);
            r = boxes[i];
        }
        i++;
    }
    return boxes_selectes;
}
int main() {
    Mat src = imread("./1.jpg", 0);
    Mat markImg = imread("./1.jpg");
    imshow("src", markImg);    
    vector<vector<Point> > points;
    vector<Rect> rects;
    Ptr<MSER> ptrMSER = MSER::create(1, 50, 10000);
    ptrMSER->detectRegions(src, points, rects);
    // 根据文字的大小筛选
    vector<Rect> boxes;
    for (int i = 0; i < rects.size(); i++) {
        if (rects[i].width < 60 && rects[i].height>60)
            boxes.push_back(rects[i]);
    }
    // 非极大值抑制
    vector<Rect> boxes_selectes = nms(boxes, 0.1);
    for (int i = 0; i < boxes_selectes.size(); i++)
        rectangle(markImg, boxes_selectes[i], Scalar(0, 255, 0), 1);
    imshow("markImg", markImg);
    waitKey(0);
    return 0;
}

参考：

1. 冈萨雷斯《数字图像处理（第四版）》Chapter 11（所有图片可在链接中下载）

2. 深度学习文本定位

posted @ 2022-11-19 11:18 湾仔码农阅读(1354) 评论(0) 编辑收藏举报

刷新页面返回顶部

FishL

博观而约取，厚积而薄发