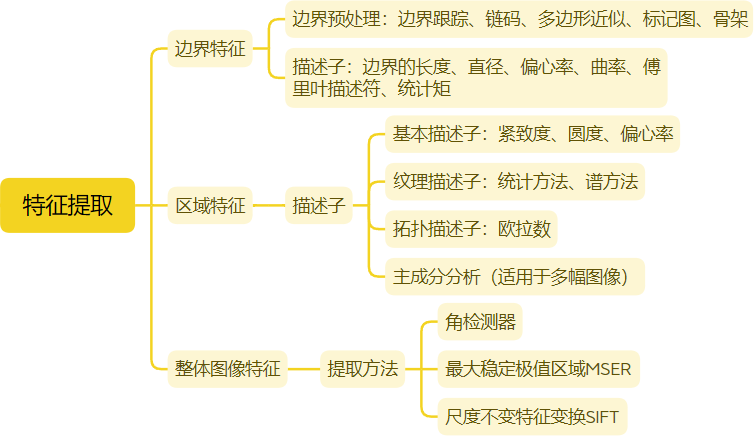
【图像处理笔记】特征提取之边界特征

0 引言

　　图像分割为多个区域或它们的边界后，需要进行特征提取，特征提取包括特征检测和特征描述。特征检测是指在边界、区域或图像中发现特征，特征描述是将定量属性分配给检测到的特征。例如，可以检测一个区域边界上的角，并用它们的方向和位置来描述这些角，其中的方向和位置都是定量属性。在特征提取之前，应尽可能利用预处理来归一化输入图像。例如，在照度变化严重到难以提取特征时，通过直方图均衡化来自动地预处理图像。基本思想是，使用极可能多的先验信息来预处理图像，以提高特征提取得准确性。

　　特征分为不变的和协变的。比如，考虑一组变换{平移，反射，旋转}，“面积”是一个不变的特征描述子。在加入{缩放}后，“面积”相对于这组变换是协变的，因为对区域面积缩放任意一个引子，也会对描述子的值缩放相同的因子。描述子“方向”（这个区域的主轴方向）也是协变的。本章大多数描述子都是协变的，最好的做法是将协变性归一化为相关的不变性。例如，通过计算一个区域的实际方向并旋转该区域，使其主轴指向预定义的方向，可以补偿这个区域方向的变化。如果对图像中检测到的每个区域都这样做，那么旋转就不再是协变的。特征的另一个主要分类是特征分为局部特征和全局特征，如果某个特征被用应用到一个集合的一个成员，那么我们称它为局部特征；如果某个特征被应用到整个集合，那么我们称它为全局特征。

1 边界预处理

分割技术产生的原始数据是一个边界上像素或一个区域内像素的形式。标准的做法是将其压缩为方便计算描述子的形式。接下来将讨论适合这一目的的各种边界预处理方法，包括：如果得到的是一个区域的像素，如何得到其边界【边界跟踪】，得到边界点后对其进行压缩（近似）【链码、多边形近似、骨架等】，以减少数据量或减少噪声干扰。

1.1 边界跟踪

在得到一个边界上或区域内的像素后，首先我们需要区域边界上的点按顺时针方向或逆时针方向排列。OpenCV提供函数cv::findContours()从二值图像中寻找轮廓(边界）。

findContours(InputOutputArray image, //通常是阈值分割或边缘检测得到二值图像
            OutputArrayOfArrays contours, //vector<vector<Point>> contours
            OutputArray hierarchy, // 轮廓的层次结构和拓扑信息
            int mode, // 轮廓的检索模式
            int method, //轮廓的近似方法
            Point offset = Point());//每个轮廓点的偏移量，可选项

关于该函数的详细讲解见链接，这边不再赘述。书上介绍了摩尔边界跟踪算法，它的输出是一个有序的点序列。我们假设（1）处理的是二值图像，图像中的目标点和背景点分别标为1和0；（2）为消除目标与图像边界合并的可能性，图像填充了0边框。为了清晰期间，我们将讨论局限于单个区域。通过逐个地处理区域，这种方法可拓展到多个不相连的区域。

以下算法跟踪二值图像中1值区域R的边界：

1. 令起点b₀是图像中最左上方标记为1的点。令c₀表示b₀的西边的零点(见上图(b))。显然，c₀总是一个背景点。从c₀开始顺时针行进，检查b₀的8邻点。令b₁表示值为1的第一个邻点，并令c₁是序列中禁止接着b₁的背景点。存储b₀的位置，以便在步骤5中使用。

2. 令b=b0,c=c0。

3. 从c开始顺时针行进，令b的8个邻点表示为n1，n2，...， n8。找到标记为1的第一个邻点，并将它表示为nk。

4. 令b=n_k，c=n_k-1；

5. 重复步骤3和4，直到b=b₀。算法停止时，找到的b个点序列就是有序边界点的集合。

示例对一个区域进行边界跟踪耗时0.02ms

vector<Point> boundaryTrack(Mat binImg) {
    uchar* b = binImg.ptr();
    int istep = binImg.cols;
    int n = 0;
    for (; n < binImg.rows * binImg.cols; n++) {
        if (*b == 255)
            break;
        b++;
    }
    int index = n;
    int end = 0;
    vector<Point> boundaryPoints;
    while (end != n) {
        boundaryPoints.push_back(Point(index % istep, index * 1.0 / istep));
        int neighbor[16] = { -istep , -istep + 1, 1, istep + 1, istep, istep - 1, -1, -istep - 1,
         -istep , -istep + 1, 1, istep + 1, istep, istep - 1, -1, -istep - 1};
        int i = 0; int gray = 0;
        for (; i < 8; i++) {
            gray = (int)b[neighbor[i]]; 
            if (gray == 0)
                break;
        }
        int j = i;
        for (; j < i + 8; j++) {
            gray = (int)b[neighbor[j]];
            if (gray != 255)
                continue;
            b+=neighbor[j];
            index += neighbor[j];
            end = index;
            break;
        }
    }
    return boundaryPoints;
}

1.2 链码

链码通过来连接规定长度和方向的直线段来表示边界。在OpenCV3之前，cv::findContours()函数可以选择CV_CHAIN_CODE，以Freeman链码的方式输出轮廓，所有其他方法输出多边形。本节假设所有都是简单的闭合曲线（即曲线是闭合的而不是自相交的）。

1.2.1 弗里曼链码

一般来说，链码表示基于线段的4连通或8连通。使用一种编号方案来对每个线段的方向进行编码，如下图所示，由这种方向数序列形成的边界码称为弗里曼链码。

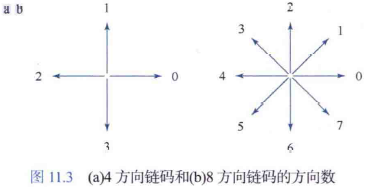
数字图像通常是再x方向和y方向以等间距的网格格式获取和处理的，因此顺时针方向跟踪边界并为连接每对像素的线段分配一个方向可以生成链码。但是，这样做会导致：（1）得到的链会相当长；（2）噪声或不完美的分割在边界的小扰动会导致链码发生与边界的主要形状特征无关的变化。解决这些问题的一种方法是，选择更大的网络间距对边界重取样，然后遍历原始边界点时，将其分配给大网格的节点。

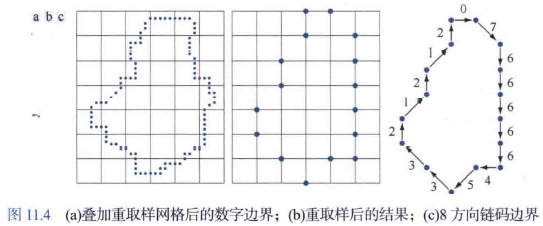
　　链码的数值取决于起点。对于闭合边界，任选一起点S得到原链码，将链码看作由各方向数构成的n位自然数，将该码按一个方向循环，使其构成的n位自然数最小，此时就形成起点唯一的链码，称为归一化链码，也称为规格化链码。我们将这样转换后所对应的链码起点作为这个边界的归—化链码的起点。也可以用一阶差分来对起点归一化。这个差分是通过计算方向变化的次数得到的，其中方向变换分隔了两个相邻的链码元素。如果将链码是为一个循环序列，并相对于起点归一化链码，那么一阶差分的第一个元素可用链码的最后一个分量和第一个分量之间的过渡计算得到。例如，4方向链码10103322的一阶差分是3133030。改变重取样的间隔实现尺寸的归一化。使用链码表示边界会明显减少存储边界所需的数据量。此外，使用链码数可为分析边界的形状提供统一的方法。

示例：弗里曼链码

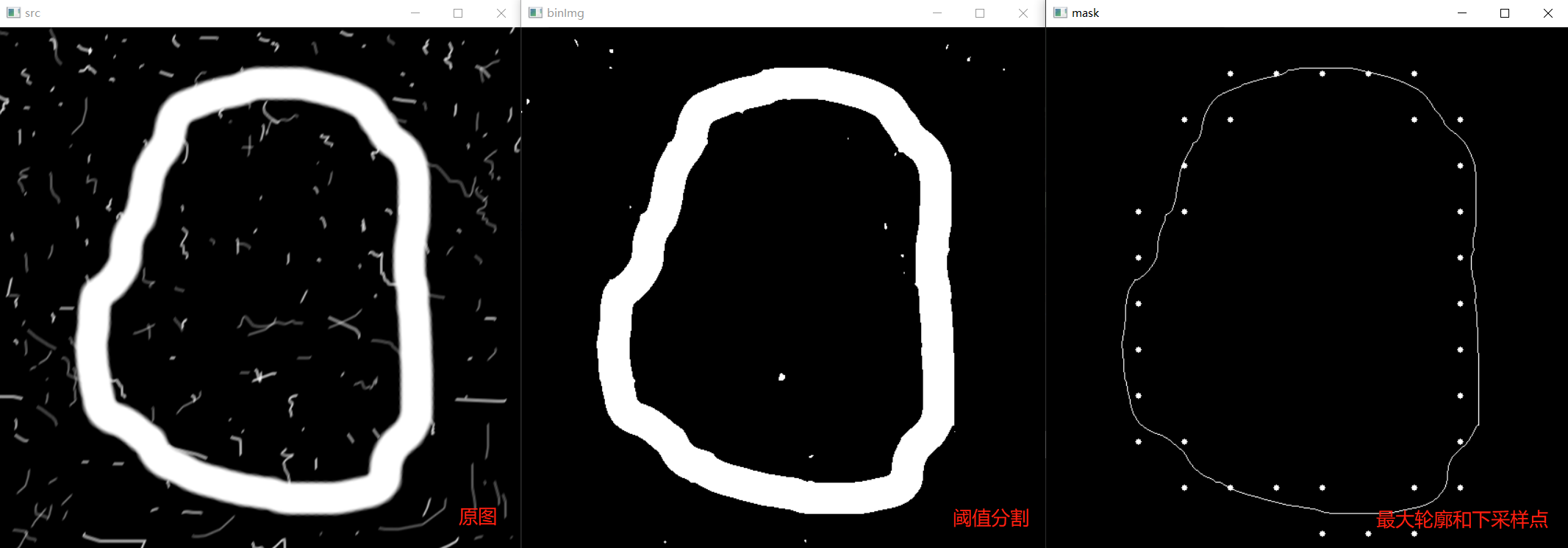
　　随机反射镜片中嵌入的一个圆形笔画的图像，大小为570×570像素的8比特灰度图像。本例的目的是得到一个弗里曼链码、幅度最小的对应整数及笔画外边界的一阶差分。由于感兴趣的目标嵌入在小镜片中，因此提取边界会产生一条噪声曲线，导致无法描述目标的一般形状。先用9×9像素的盒式核平滑原图像，再利用Otsu对图像进行全局阈值处理。直接得到外边界的链码会导致一个具有较小变化的长序列，它不能代表边界的全局形状，因此重定义这个边界。本例使用节点间距为50像素的重取样网格，这种较为简单的近似保留了原边界的主要特征。

#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;

// 1361点下采样为35点，首尾相交
void subsamplePoints(vector<Point>& pts1, vector<Point>& pts2, int gridsep) {
    pts2.clear();
    for (size_t i = 0; i < pts1.size(); i++) {
        int x = pts1[i].x * 1.0 / gridsep + 0.5;
        int y = pts1[i].y * 1.0 / gridsep + 0.5;
        Point p = Point(x * gridsep, y * gridsep);
        if(pts2.size()==0 || p!= pts2.back())
            pts2.push_back(p);
    } 
}
// 默认的Point由于不能比较大小,故无法作为map的键值,此处提供比较方法
class cmpPoints :public binary_function<Point, Point, bool>
{
public:
    bool operator()(const Point& p1, const Point& p2) const
    {
        return p1.x < p2.x || p1.y < p2.y;
    }
};
// 确定p2相对于p1的方向
Point cmp(Point& p1, Point& p2) {
    int dx = p2.x - p1.x;
    if (dx > 0) dx = 1;
    if (dx < 0) dx = -1;
    int dy = p2.y - p1.y;
    if (dy > 0) dy = 1;
    if (dy < 0) dy = -1;
    return Point(dx, dy);
}
// 生成链码
void FreemanChainCode(vector<Point>& pts) {
    map<Point, int, cmpPoints> mymap = { {Point(1, 0), 0}, {Point(1, 1), 1}, {Point(0, 1), 2}, {Point(-1, 1),3}, {Point(-1, 0), 4},
                              {Point(-1, -1), 5}, {Point(0, -1), 6}, {Point(1, -1), 7}};
    for (size_t i = 0; i < pts.size()-1; i++) {
        Point p = cmp(pts[i], pts[i + 1]);
        cout << mymap[p] << " ";
    }
}
int main()
{
    Mat markImg = imread("./1.tif");
    Mat src, binImg;
    cvtColor(markImg, src, COLOR_BGR2GRAY);
    boxFilter(src, src, -1, Size(5, 5));// 9×9盒式滤波器（半径为5）
    threshold(src, binImg, 200, 255, THRESH_OTSU);// 大津阈值法
    // 找最大轮廓
    vector<vector<Point>> contours;
    findContours(binImg, contours, RETR_EXTERNAL, CHAIN_APPROX_NONE);//simple模式少点
    int max_idx = 0; double max_area = 0.0;
    for (size_t i = 0; i < contours.size(); i++)
    {
        double area = contourArea(contours[i]);
        if (max_area < area) {
            max_area = area;
            max_idx = i;
        }
    }
    Mat mask = Mat::zeros(src.size(), CV_8U);
    drawContours(mask, contours, max_idx, Scalar(255), 1);
    // 下采样轮廓点
    vector<Point> subPoints;
    subsamplePoints(contours[max_idx], subPoints, 50);
    for (size_t k = 0; k < subPoints.size(); k++) {
        circle(mask, subPoints[k], 3, Scalar(255), -1);
    }
    // 生成链码
    FreemanChainCode(subPoints);//4 4 2 4 2 2 4 2 2 2 2 2 0 2 0 0 0 2 0 0 6 0 6 6 6 6 6 6 6 6 4 6 4 4
    return 0;
}

1.2.2 斜率链码

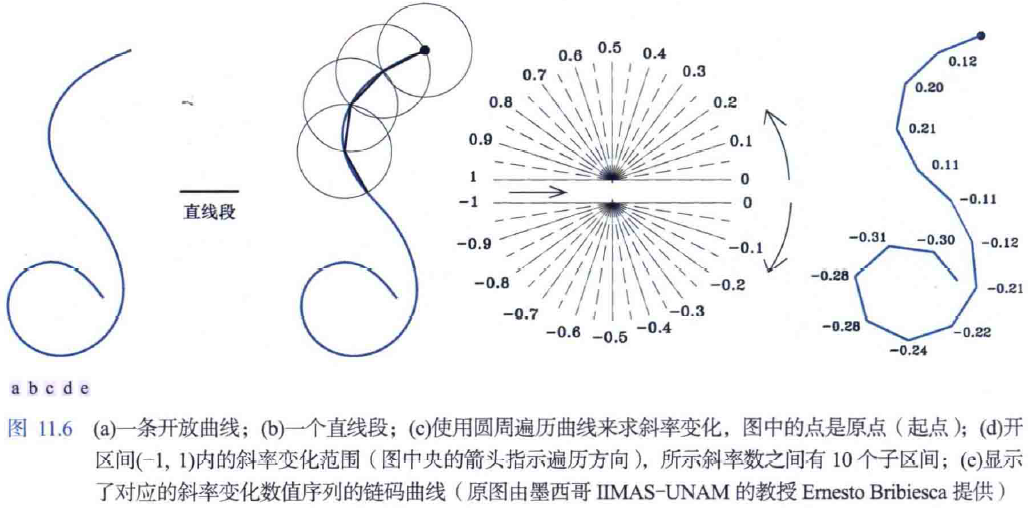
　　使用弗里曼链码时，通常要求重取样边界来平滑小的变化，这意味着首先要定义一个网格，然后将所有的边界点分配给网格中最近的邻点。这种方法的一种替代方式是使用斜率链码(SCC)。二维曲线的SCC是通过在曲线周围放置等长的直线段得到的，其中直线段的端点与曲线相接。要得到SCC，就要计算相邻直线段之间的斜率变化，并将斜率变化归一化到连续的（开）区间(-1,1)。这种方法需要定义直线段的长度，而弗里曼链码则要求定义一个网格并将曲线点分配给网格，因此后者更复杂。和弗里曼链码一样，SCC是旋转独立、平移独立的，但是更大范围内的斜率变化提供了更精确的表示。下图说明了如何生成SCC。利用半径为直线段长度的圆与曲线的交点得到链码的节点，即可求到斜率的变化。感觉好像不太用得到，暂时就不去实现了。

1.3 用最小周长多边形近似边界

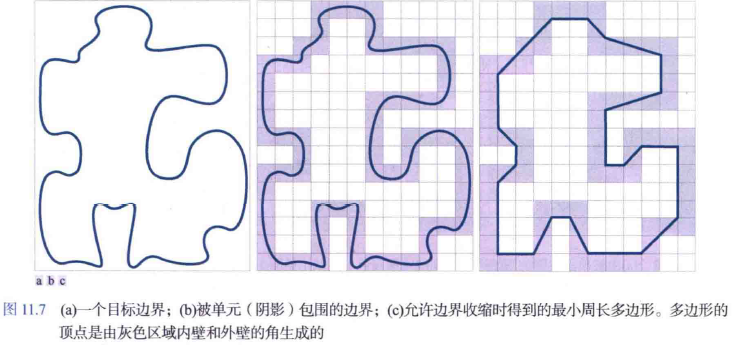
多边形近似的目的是使用数量尽可能少的线段来得到给定边界的基本形状。一般来说这个问题并不简单，可能会变成耗时的迭代搜索。最有效的方法之一是使用最小周长多边形（MPP）来表示边界。

OpenCV 中的函数cv::approxPolyDP()可以用于对图像轮廓点进行多边形拟合。

void approxPolyDP( InputArray curve,//存储在std::vector或Mat中的2D曲线点集
                   OutputArray approxCurve,//输出点集，表示拟合曲线或多边形，数据与输入参数 curve 一致
                   double epsilon, //用于指定逼近精度的参数，为原始曲线与逼近曲线的最大距离
                   bool closed );//闭合标志，True 表示闭合多边形，False 表示多边形不闭合

示例多边形近似边界

...同上个例子
vector<Point> contours_ploy;
approxPolyDP(contours[max_idx], contours_ploy, 15, true);
for (int j = 0; j < contours_ploy.size() - 1; j++)
{
    line(mask, contours_ploy[j], contours_ploy[j+1],Scalar(0, 255, 0));
}
line(mask, contours_ploy[0], contours_ploy[contours_ploy.size() - 1], Scalar(0, 255, 0));

1.4 标记图

标记图是二维边界的一维函数表示，它可以由各种方式生成。最简单的方式之一是把质心到边界的距离画成角度的函数，如下图所示。使用标记图的基本思想是将边界表示简化为一维函数，因为一维函数与原始的二维边界相比更容易描述。

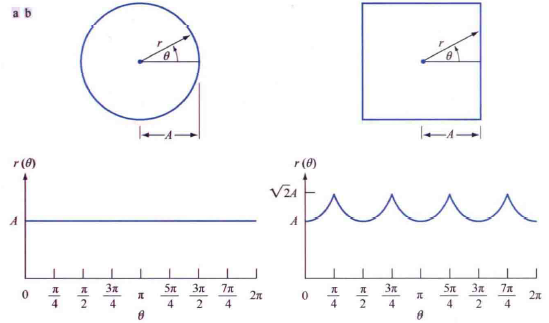
由于形状大小的变化会导致对应标记图的幅值发生变化，我们可以放缩所有函数，使它们的值域相等。这个方法的优点是简单，但缺点是放缩只取决于最大最小值，如果有噪声，会出现明显的误差。一种更好但计算量更大的方法是让每个样本除以标记图的方差。无论哪种方法，中心思想都是消除对尺寸的依赖性，同时保留波形的基本形状。

1.5 骨架

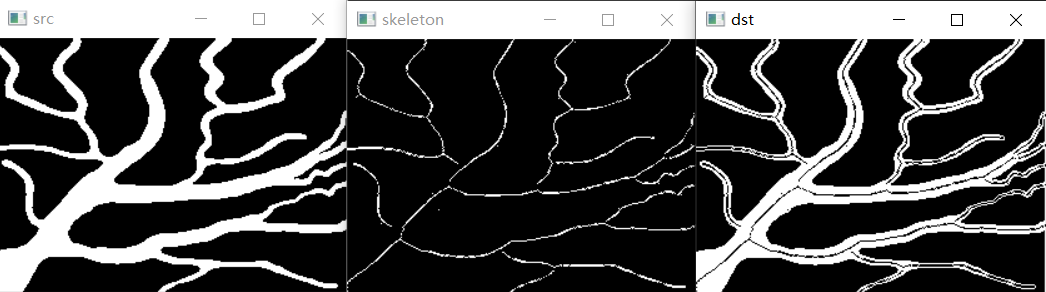
骨架与区域的形状有关，可由边界计算。可以采用如下两种方式之一获取骨架：（1）保持端点和线的连通性的同时，连续细化区域；（2）通过有效实现 Blum提出的中轴变化MAT来计算其区域的中轴。【图像处理笔记】二值图像形态学中讨论过细化，接下来会再用形态学腐蚀进行细化。具有边界B的区域R的MAT如下：对于R中的每个点p，在B中找到它的最近邻点。如果p有多个这样的邻点，那么它属于R的中轴。“最近”的概念取决于距离测量的定义。根据草原大火的概念，可以直观地解释一个区域的MAT。我们可以将一个图像区域视为一片均匀的、干燥的草地，并假设同时在边界的所有点处点火。所有的燃烧前沿会以同样的速度进入这个区域。这个区域的MAT是由一个以上的燃烧前沿在同一时间到达的点的集合。一般来说，与细化处理相比，MAT更容易产生有意义的骨架。然而，计算一个区域的MAT需要计算每个内部点到区域边界上的每个点的距离，而这在大多数应用中是不切实际的。相反，这种方法由距离变换等效地得到骨架。

示例形态学提取骨架

Mat src = imread("./1.png", 0);
Mat binImg, erodeImg, openImg, subImg;
Mat skeleton = Mat::zeros(src.size(), CV_8U);
threshold(src, binImg, 0, 255, THRESH_OTSU);
Mat ele = getStructuringElement(MORPH_CROSS, Size(3, 3));
while (true) {
    morphologyEx(binImg, erodeImg, MORPH_ERODE, ele);
    morphologyEx(erodeImg, openImg, MORPH_OPEN, ele);
    subtract(erodeImg, openImg, subImg);
    skeleton.setTo(255, subImg);
    binImg = erodeImg;
    if (!countNonZero(openImg))
        break;
}

2 边界特征描述子

2.1 基本边界描述子

长度：边界上的像素数量是边界长度的近似。用链码（间距为1）表示边界时，长度是垂直分量的数量+水平分量的数量+√2对角分量的数量；用多边形表示边界时，长度等于多边形各条边的长度之和。

直径：选定距离测度，在边界上两点之间的距离的最大值为直径。这两个点连接的直线段为长轴，边界的短轴定义为垂直于长轴的直线。

偏心率：长轴与短轴之比称为边界的偏心率。

曲折度：定义为斜率的变化率。一般来说，原始数字边界上某点处的曲折度不可靠，因为这些边界往往是局部“粗糙”的。平滑可能会有帮助，更有效的是多边形近似后，计算相邻边界直线段的斜率之差。在这种情况下，我们只关注顶点处的曲折度。顺时针方向遍历多边形时，如果顶点p处的斜率变化是非负的，那么顶点是凸顶点，否则称顶点为凹顶点。使用斜率变化范围可以进一步细化这一描述。例如，顶点p处斜率的绝对变化小于10°时，顶点p就标记为近直线段的一部分；斜率的绝对变化在90°±30°范围时，顶点p标记为“类角”点。将边界表示为斜率链码时，曲折度为链元素的绝对值之和，很容易表示。

示例使用斜率链码描述曲折度

　　血管形态学的一个重要测度是血管曲折度。这个指标有助于早产儿视网膜病变ROP的计算机辅助诊断。ROP会使得视网膜内的血管异常生长，进而使得视网膜脱离眼睛的后部，最终导致失明。下图显示了一名新生儿的视网膜图像。眼科医生根据视网膜血管的外观对ROP的初始治疗进行诊断和决策。我们提取了每条血管的边界，并计算了其长度（像素数）P。为了使得SCC比较有意义，我们归一化了三个边界，使得每个边界都有相同数量m的直线段。因此，每个SCC的元素的数量为m-1。由一个SCC表示的曲线的弯折度定义为链元素的绝对值之和。下表显示了基于51个直线段的A、B和C血管的弯曲度。曲折度的值与我们对三条血管的视觉分析结果一致，B的曲折度稍大于A的曲折度，C的曲折度最小。

2.2 形状数

　　4方向弗里曼链码边界的形状数定义为最小幅度的一阶差分。最小幅度是指，在不改变循环的相对位置基础上重新排列的数列，使数列最小。例如下面的链码003221，重点在第一个差分数，它等于链码尾1到链码头0需要改变方向的次数3，3是最大的，将链码排列为首位一致，第一个差分数即为0，此时的一阶差分是幅度最小的。形状数的阶n定义为一阶差分表示中的数字的数量。此外，对于封闭边界，n是偶数，它的值限制了不同形状的数目。

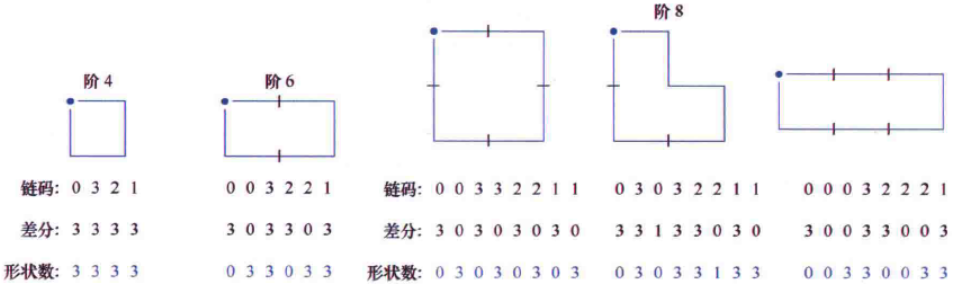
示例计算形状数

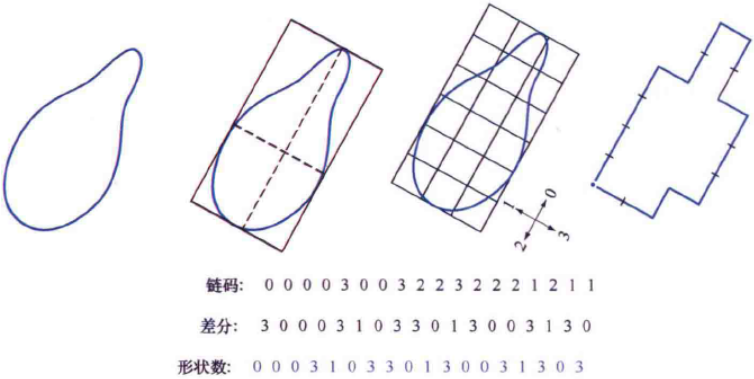
假设要得到下图边界阶为18的一个形状数。首先，找到最小外接矩形。接着找到最接近的18阶矩形，是3×6的矩形。链码方向与生成的网格对齐。最后是得到链码，并使用其一阶差分来计算形状数。

2.3 傅里叶描述子

　　傅里叶描述子（Fourier shape descriptors）的基本思想是用目标边界曲线的傅里叶变换来描述目标区域的形状，将二维描述问题简化为一维描述问题。傅里叶描述子具有旋转、平移和尺度不变性。其最主要的作用之一是应用在形状识别中，如字符识别。

将组成边界的K个坐标对(x₀,y₀)，(x₁,y₁)，···，(x_K-1,y_K-1)视为复数，于是有s(k)=x(k)+jy(k)，式中，k=1,2,···,K-1。s(k)的傅里叶变换(DFT)是

式中，u=1,2,···,K-1。复数系数a(u)称为边界的傅里叶描述子。这些系数的傅里叶反变换可以恢复s(k)，也就是利用傅里叶描述子进行重建边界。如果用了所有的傅里叶级数，那么反变换就等于原输入，但假设只使用前P个系数，即对u>p-1令a(u)= 0，此时的结果对反变换的s(k)有如下近似：

参数k的值域仍然是0到K-1，即近似边界中存在相同数量的点，但是未在每个点的重建中使用那么多项。注意：

重建过程和频率域低通滤波是一样的，都是删除高频系数，保留低频然后在反变换。高频分量决定细节，而低频分量决定整体形状。因此删除的系数越多，边界上丢失的细节越多。
DFT的周期性要求我们在对变换滤波前，先将这个变换乘以(-1)x以便使其去中心化。同时，在反变换时再次使用它来去中心化。
由于DFT的对称性，边界上的点数及其反变换必须是偶数。这意味着在计算反变换之前，删除的系数（置为0）数量必须是偶数。因为变换已被中心化，所以我们将变换两端的一半数量的系数设为0，以便保持对称性。

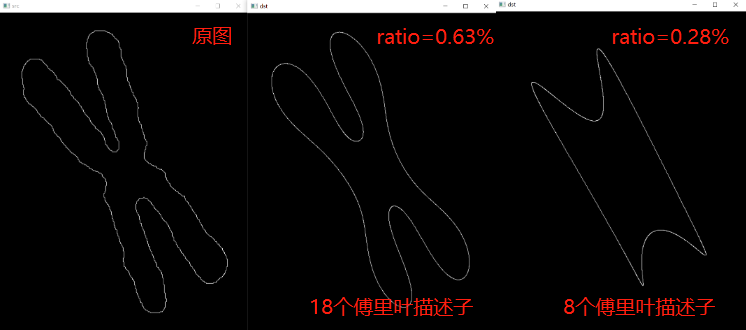
示例使用傅里叶描述子

下图显示了人类染色体的边界，它由2868个点组成，利用傅里叶变换得到对于的2868个傅里叶描述子。本例的目的是建业使用较少傅里叶描述子重建边界的效果。可以看出，只用18个描述子就可以保留原边界的主要形状特征：4个长凸起和2个深弯。

#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;

void FourierShapeDescriptors(vector<Point>& contour, double ratio, vector<Point>& output_contour)
{
	//1. 将轮廓变为复数图像
	Mat pointMat(contour.size(), 1, CV_32FC2); 
	Vec2f* p = pointMat.ptr<Vec2f>();
	for (size_t i = 0; i < contour.size(); i++)
	{
		p[i][0] = (float)contour[i].x;
		p[i][1] = (float)contour[i].y;
	}
	//2. 计算离散傅里叶变换的最优尺寸
	Mat paddedMat;
	int m = getOptimalDFTSize(pointMat.rows);
	int n = getOptimalDFTSize(pointMat.cols);
	copyMakeBorder(pointMat, paddedMat, 0, m- pointMat.rows, 0, n - pointMat.cols, BORDER_CONSTANT, Scalar::all(0));
	//3. 中心化
	p = paddedMat.ptr<Vec2f>();
	for (size_t i = 0; i < m; i++)
	{
		if (i % 2 != 0){
			p[i][0] = - p[i][0];
			p[i][1] = - p[i][1];
		}
	}
	//4. 傅里叶变换
	Mat dftMat;
	dft(paddedMat, dftMat, DFT_COMPLEX_INPUT | DFT_COMPLEX_OUTPUT);
	
	//5. 保留重构边界的描述子
	int number = cvRound(m * ratio) & -2; // a & -2 代表最大不超过a的偶数
	int number_remove = (m - number) / 2;
	dftMat.rowRange(0, number_remove) = Scalar::all(0);	//删除系数(设置为0)
	dftMat.rowRange(dftMat.rows - number_remove, dftMat.rows) = Scalar::all(0);
	//6. 傅里叶反变换
	Mat idftMat;
	idft(dftMat, idftMat, DFT_COMPLEX_INPUT | DFT_COMPLEX_OUTPUT | DFT_SCALE);
	//7. 去中心化
	p = idftMat.ptr<Vec2f>();
	for (size_t i = 0; i < m; i++)
	{
		if (i % 2 != 0) {
			p[i][0] = -p[i][0];
			p[i][1] = -p[i][1];
		}
	}
	//8. 裁剪为原来大小
	Mat dst = idftMat.rowRange(0, contour.size()).clone();
	dst.convertTo(dst, CV_32SC2);

	//9. 由图像Mat变回轮廓点vector<Point>
	Point point;
	for (size_t i = 0; i < contour.size(); i++)
	{
		point.x = dst.ptr<cv::Vec2i>(i)[0][0];
		point.y = dst.ptr<cv::Vec2i>(i)[0][1];
		output_contour.push_back(point);
	}
}

int main() {
	Mat src = imread("./4.tif", 0);
    Mat binImg;
    threshold(src, binImg, 50, 255, THRESH_BINARY);
    vector<vector<Point>> contours;
    findContours(binImg, contours, RETR_EXTERNAL, CHAIN_APPROX_NONE);
	Mat markImg = Mat::zeros(src.size(), CV_8U);
	vector<Point> output_contour;
	FourierShapeDescriptors(contours[0], 0.0028, output_contour);
	vector<vector<Point>> output_contours={ output_contour };
	drawContours(markImg, output_contours, 0, Scalar(255), 1);
    return 0;
}

2.4 统计矩

就像标记图那样，变量的统计矩是适用于二维边界的一维表示的有用描述子。1.4节的标记图，可以视为变量r的一个普通离散函数g(r)，令g(r)=z，形成直方图p(z)，将p归一化，使其元素之和等于1，那么p(z)就是值z出现的概率估计。z关于其平均值的n阶矩是

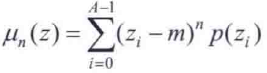
其中m是z的均值，A是不同z的个数。一阶矩与标记图的形状直接相关，二阶矩度量曲线相对于直线平均值的扩展程度，三阶矩则是关于平均值的对称性的测量。OpenCV 提供了函数cv::moments()计算图像矩

Moments moments( InputArray array, //输入参数可以是光栅图像(单通道、8位或浮点的二维数组)或二维数组；
                 bool binaryImage = false );//默认值false。若此参数取true，则所有非零像素为1,此参数仅对于图像使用

当输入是边界点时，返回的矩常用来计算质心坐标x=m10/m00，y=m01/m00（也可以用cv::connectedComponentsWithStats计算质心）；以及边界包围的面积area = m00(和cv::contourArea一样)。

示例用矩计算边界中心

Mat src = imread("./3.png", 0);
Mat binImg;
threshold(src, binImg, 50, 255, THRESH_BINARY);
vector<vector<Point>> contours;
findContours(binImg, contours, RETR_EXTERNAL, CHAIN_APPROX_NONE);
Mat markImg = Mat::zeros(src.size(), CV_8UC3);
drawContours(markImg, contours, -1, Scalar(255, 255, 255), 1);
vector<Point2f> centroid(contours.size());
for (int i = 0; i < contours.size(); i++)
{
	Moments m = moments(contours[i], false);
	Point centroid(m.m10 / m.m00, m.m01 / m.m00);
	circle(markImg, centroid, 3, Scalar(0, 255, 0), -1);
}