【图像处理笔记】图像分割之区域生长、区域分离与聚合
0 引言
本章的大多数分割算法都基于图像灰度值的两个基本性质之一:不连续性和相似性。第一类方法根据灰度的突变(如边缘)将图像分割为多个区域:首先寻找边缘线段,然后将这些线段连接为边界的方法来识别区域。第二类方法根据一组预定义的准则把一幅图像分割为多个区域:上一节根据像素性质(如灰度值或颜色)的分布进行阈值分割;本节将讨论直接寻找区域的分割技术。
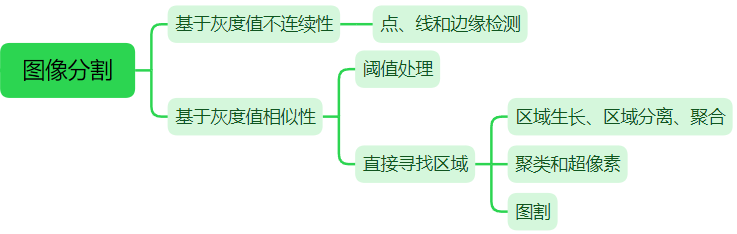
1 区域生长
区域生长是指根据预定义的准则,将像素或子区域组合为更大区域的过程。是以区域为处理对象,基于区域内部和区域之间的同异性,尽量保持区域中像素的临近性和一致性的统一 。
区域生长的基本方法是,对于一组“种子”点,通过把与种子具有相同预定义性质(如灰度或颜色范围)的邻域像素合并到种子像素所在的区域中,再将新像素作为新的种子不断重复这一过程,直到没有满足条件的像素为止。
- 种子点的选取经常采用人工交互方法实现,也可以寻找目标物体并提取物体内部点,或利用其它算法找到的特征点作为种子点。
- 相似性准则的选取不仅取决于所考虑的问题,而且取决于可用图像数据的类型。图像是单色图像时,必须使用一组基于 灰度级和空间性质的描述子(如矩或纹理)来分析区域。
- 区域生长过程中要考虑连通性,将灰度级相同的像素组合为一个区域而不考虑连通性,会得到毫无意义的分割结果。
- 区域生长还需制定停止规则。不再有像素满足加入某个区域的准则时,这个区域生长就应停止。像灰度值、纹理和彩色这样的准则,本质上是局部准则,都未考虑区域生长的“历史”。可以使用大小、候选像素与迄今为止已生长像素之间的相似度(比如平均灰度)、正在增长的区域形状等。
区域生长方法的步骤:
(1)对图像自上而下、从左向右扫描,找到第 1 个还没有访问过的像素,将该像素作为种子 (x0, y0);
(2)以 (x0, y0) 为中心, 考虑其 4 邻域或 8 邻域像素 (x, y),如果其邻域满足生长准则 则将 (x, y) 与 (x0, y0) 合并到同一区域,同时将 (x, y) 压入堆栈;
(3)从堆栈中取出一个像素,作为种子 (x0, y0) 继续步骤(2);
(4)当堆栈为空时返回步骤(1);
(5)重复步骤(1)-(4),直到图像中的每个点都被访问过,算法结束。
示例 使用区域生长分割图像
下面是焊缝(水平深色区域)的8比特X射线图像,图像中含有几条裂缝和孔隙(水平横贯图像中心的明亮区域)。下面通过分割这个有缺陷的焊缝区域来说明区域生长的应用。这些区域可用在焊缝检测或自动焊接系统控制等应用中。
#include<opencv2/opencv.hpp>
using namespace std;
using namespace cv;
void regionGrow(Mat& src, Mat& mask, vector<Point>& seeds, int thresh, Mat& dst){
dst = Mat::zeros(src.size(), CV_8UC1);
while(seeds.size()>0){
Point currentPoint = seeds.back();
dst.at<uchar>(currentPoint.y, currentPoint.x) = 255;// 将对应位置的点标记为255
seeds.pop_back(); //标记后就删
Point dps[] = { Point(-1,-1), Point(0,-1), Point(1,-1), Point(1,0), Point(1,1), Point(0,1), Point(-1,1), Point(-1,0) };
for (size_t i = 0; i < 8; i++)// 8邻接连通
{
Point tmpPoint = currentPoint + dps[i];
if (!tmpPoint.inside(Rect(0, 0, src.cols, src.rows))) continue;//判断是否出界
// 计算灰度差
int gray_diff = src.at<uchar>(currentPoint.y, currentPoint.x) - src.at<uchar>(tmpPoint.y, tmpPoint.x);
if (abs(gray_diff) < thresh && dst.at<uchar>(tmpPoint.y, tmpPoint.x) == 0 && mask.at<uchar>(tmpPoint.y, tmpPoint.x) == 255)
seeds.push_back(tmpPoint);
}
}
}
int main() {
Mat src = imread("./16.tif", 0);
Mat markImg;
cvtColor(src, markImg, COLOR_GRAY2BGR);
Mat binImg, mask, dst;
threshold(src, binImg, 254, 255, THRESH_BINARY);// 高阈值产生种子区域
Mat labels, stats, centroids; // 连通域,获得质心点
int nccomps = connectedComponentsWithStats(binImg, labels, stats, centroids);
vector<Point> seeds;
for (size_t i = 0; i < nccomps; i++)
{
Point p((int)centroids.at<double>(i,0), (int)centroids.at<double>(i, 1));
if (src.at<uchar>(p.y, p.x) > 200)
//circle(markImg, p, 1, Scalar(0, 255, 0));
seeds.push_back(p);
}
threshold(src, mask, 190, 255, THRESH_BINARY);
regionGrow(src, mask, seeds,50, dst);
return 0;
}


2 区域分离与聚合
区域分离与聚合算法的基本思想是将图像细分为一组不相交的区域,然后聚合或者分离这些区域。分离和聚合的判据是用户选择的谓词逻辑 Q,通常是目标区域特征一致性的测度,例如灰度均值和方差。分离过程先判断当前区域是否满足目标的特征测度,如果不满足则将当前区域分离为多个子区域进行判断;不断重复判断、分离,直到拆分到最小区域为止。区域分离的分割结果通常包含具有相同性质的邻接区域,通过聚合可以解决这个问题。仅当邻接区域的并集满足目标的特征测度,才将进行聚合。
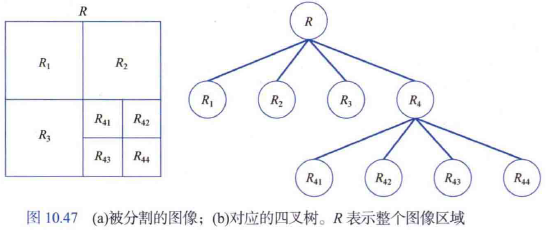
区域分离与聚合过程如下:
(1)把所有满足条件 Q(Ri)=False 的任何区域Ri分离为4个不相交的子区域;
(2)无法进一步分离时,把所有满足条件 Q(Rj∪Rk)=True 的相邻区域 Rj, Rk聚合;
(3)无法进一步聚合时,停止操作。
在步骤(2)中也可以简化为,两个邻接区域都各自满足条件是,聚合这两个区域。如下例所示,这一简化仍然能够产生较好的分割结果。
示例:使用区域分离和聚合分割图像
下面是天鹅星座环的一幅大小为566×566的X射线波段图像。本例的目的是分割(从图像中提取)围绕致密内部区域的“环装”松散物质。感兴趣区域中像素的平均灰度不超过125,并且标准差总是大于10。将四分区域的最小尺寸从32变到8的结果如下所示。其中,16×16的四分区域在捕捉外部区域的形状方面效果最好,8×8的四分区域结果中有一些黑色小方块,四分区域越小,小方块越多。在所有的情况下,分割后的区域是一个连通区域,完全分隔了平滑的内部区域和背景。因此有效地把图像分成了3个不同的区域,对应于图像中的三个主要特征:背景、致密区域和稀疏区域。
#include<opencv2/opencv.hpp>
using namespace std;
using namespace cv;
void splitMerge(Mat& src, Mat& dst, int h0, int w0, int h, int w, int maxMean, int minStd, int cell) {
Rect r = Rect(w0, h0, w, h) & Rect(0, 0, src.cols, src.rows);// 防止出界
Mat win = src(r);
Mat mean, stddev;
meanStdDev(win, mean, stddev);// 计算均值和标准差
if (mean.at<double>(0, 0) < maxMean && stddev.at<double>(0, 0) > minStd && h < 2 * cell && w<2 * cell)
// 满足条件,判为目标区域,设为白色
rectangle(dst, r, Scalar(255), -1);
else // 不满足条件
if(h>cell && w>cell){// 继续拆分
splitMerge(src, dst, h0, w0, (h + 1) / 2, (w + 1) / 2, maxMean, minStd, cell);
splitMerge(src, dst, h0+ (h + 1) / 2, w0, (h + 1) / 2, (w + 1) / 2, maxMean, minStd, cell);
splitMerge(src, dst, h0, w0+ (w + 1) / 2, (h + 1) / 2, (w + 1) / 2, maxMean, minStd, cell);
splitMerge(src, dst, h0 + (h + 1) / 2, w0 + (w + 1) / 2, (h + 1) / 2, (w + 1) / 2, maxMean, minStd, cell);
}
}
int main() {
Mat src = imread("./17.tif", 0);
Mat dst32 = Mat::zeros(src.size(), CV_8UC1);
Mat dst16 = Mat::zeros(src.size(), CV_8UC1);
Mat dst8 = Mat::zeros(src.size(), CV_8UC1);
// 均值上界和标准差下界,最小分割区域 cell=32, 16, 8
int maxMean = 95; int minStd = 10;
splitMerge(src, dst32, 0, 0, src.cols, src.rows, maxMean, minStd, 32);
splitMerge(src, dst16, 0, 0, src.cols, src.rows, maxMean, minStd, 16);
splitMerge(src, dst8, 0, 0, src.cols, src.rows, maxMean, minStd, 8);
imshow("src", src);
imshow("32x32", dst32);
imshow("16x16", dst16);
imshow("8x8", dst8);
waitKey(0);
return 0;
}

参考
1. 冈萨雷斯《数字图像处理(第四版)》Chapter 10(所有图片可在链接中下载)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号