霍夫变换原理及实现(Opencv C++)
已知一幅图像中的n个点,假设我们希望找到这些点中位于直线上的子集。一种可能的解决方法是,首先找到由每对点确定的所有直线,然后寻找靠近特定直线的那些点的所有子集。这种方法涉及寻找n(n-1)/2~n2条直线,然后将每个点与所有直线执行n(n(n-1))/2~n3次比较。在大多数应用中,这都是一项困难的计算任务。
原理
Hough提出了一种替代方法,通常称为霍夫变换。令(xi,yi)表示xy平面上的一点,并考虑一条直线的斜截式的通用公式yi=axi+b。过点(xi,yi)的直线有无数条,并且对于a和b的不同值,它们都满足公式yi=axi+b。然而,将该个公式写为b=-axi+yi,并考虑ab平面(也称为参数空间),将得到固定点(xi,yi)的单条直线的公式。此外,第二个点(xj,yj)在ab平面也有一条与之相关联的直线,它在ab平面中与(xi,yi)相关的直线在某个点(a',b')相交,其中a'是斜率,b'是包含xy平面中(xi,yi)和(xj,yj)的直线的截距(当然,我们假定这些直线不平行)。事实上,这条直线上的所有点在参数空间中都有相交于点(a',b')的直线。
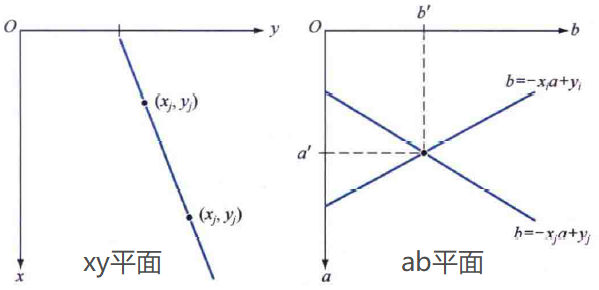
理论上,我们可以画出对应xy平面中的所有点(xk,yk)的参数空间直线,并且平面中的主要直线可以通过标志参数空间中大量直线相交的那些点来找到。然而,这种方法的一个难点是,当直线趋近于垂直方向时,a(直线的斜率)趋于无穷大。解决这个难点的方法之一是使用极坐标系:
![]()
水平直线有θ=0°,ρ等于正x截距。类似地,垂直直线有θ=90°,ρ等于正y截距;或者有θ=-90°,ρ等于负y截距。下图b中每条正弦曲线表示过xy平面中某点(xk,yk)的直线族。交点(ρ',θ')对应于图a中过点(xi,yi)和(xj,yj)的直线。

步骤
霍夫变换计算上的优点是可将ρθ参数空间划分为多个累加单元,如上图c所示,其中(ρmin, ρmax)和(θmin, θmax)是期望的参数范围:-90°≤θ≤90°和-D≤ρ≤D,D是图像中对角之间的最大距离。坐标(i,j)处具有累加值A(i,j)的单元对应于与参数空间坐标(ρi,θj)相关联的方格。具体步骤为:
(1)将这些单元设置为零;
(2)对xy平面的每个非背景点(xk,yk),令等于轴上每个允许的细分值,同时用方程ρ=xkcosθ+yksinθ解对应的ρ;
(3)将得到的值四舍五入到轴上最接近的允许单元值。若选择一个θq值后得到解ρ,则令A(p,q)+=1
循环(1)-(3)步,直至遍历完xy平面所有点,此时单元A(i,j)的k值意味着有k个点位于直线xkcosθ+yksinθ=ρ上。ρθ平面的细分数量决定能够这些点共线的精度。这种方法的计算次数与xy平面中非背景点的数量n成线性关系。
示例:下图为101×101像素的图,带有5个白点
#include<opencv2/opencv.hpp>
using namespace std;
using namespace cv;
void drawLine(Mat& markImg, int theta, int p) {
Point p1 = Point(int(p / sin(theta * CV_PI / 180)),0);
Point p2 = Point( int((p- (markImg.cols-1)*cos(theta * CV_PI / 180)) / sin(theta * CV_PI / 180)), markImg.cols - 1);
line(markImg, p1, p2, Scalar(0, 255, 0));
}
int main() {
int arr[180][142]={0};
Mat src = imread("./9.bmp", 0);
Mat markImg;
cvtColor(src, markImg, COLOR_GRAY2BGR);
for (int i = 0; i < src.rows; i++) {
for (int j = 0; j < src.cols; j++) {
if (src.at<uchar>(i, j) == 255) {
for (int theta = 0; theta < 180; theta++) {
int p = (int)round(i*cos(theta*CV_PI / 180)+j*sin(theta*CV_PI / 180)) ;
arr[theta][p] += 1;
}
}
}
}
for (int i = 0; i < 180; i++) {
for (int j = 0; j < 142; j++) {
if (arr[i][j] > 2)
drawLine(markImg, i, j);
}
}
imshow("src", src);
imshow("dst", markImg);
waitKey(0);
return 0;
}


cv::HoughLinesP
Opencv实现了以下三种霍夫线变换:
1.标准霍夫变换
提供一组参数对(ρi,θj)的积极和来表示检测到的直线,在opencv中通过函数HoughLines实现。
2.多尺度霍夫变换
3.累积概率霍夫变换
执行起来效率更高,输出检测到的直线的端点(x0,y0,x1,y1),在opencv中通过函数HoughLinesP实现。
void HoughLinesP( InputArray image, OutputArray lines, double rho, // rho 的步长 double theta, // 角度的步长,单位是度 int threshold, // 阈值 double minLineLength=0, // 线段的最小长度 double maxLineGap=0 ); // 线段之间的最小距离
示例:机场航拍图像找跑道
#include<opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int main() {
Mat src = imread("./9.tif", 0);
Mat markImg,gauImg, cannyImg;
cvtColor(src, markImg, COLOR_GRAY2BGR);
GaussianBlur(src, gauImg, Size(5, 5), 0);
Canny(gauImg, cannyImg, 120, 260, 3);
// 标准霍夫变换,直线检测
vector<Vec4i> lines;
HoughLinesP(cannyImg, lines, 1, CV_PI / 180.0, 100, 120, 20);
for (int i = 0; i < lines.size(); i++)
{
line(markImg, Point(lines[i][0], lines[i][1]), Point(lines[i][2], lines[i][3]), Scalar(0, 255, 0), 1, 8, 0);
}
imshow("src", src);
imshow("dst", markImg);
waitKey(0);
return 0;
}

参考:
1. 冈萨雷斯《数字图像处理(第四版)》Chapter 9 (所有图片可在链接中下载)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号