Canny边缘检测实现(Opencv C++)
Canny边缘检测是Canny在1986年提出来的,目前仍是图像边缘检测算法中最经典、先进的算法之一。canny方法基于如下三个基本目标:
1. 低错误率:所有边缘都应被找到,并且不应有虚假响应。
2. 最优定位:已定位的边缘必须尽可能接近真实边缘 。也就是说,由检测子标记为边缘的一点和真实边缘的中心之间的距离应最小。
3. 单个边缘点响应:对于每个真实的边缘点,检测子应只返回一个点。也就是说,真实边缘周围的局部最大数应该是最小的。这意味着检测子不应识别只存在单个边缘点的多个边缘像素。
canny的工作本质是,从数学上表达了前三个准则,并试图找到这些公式的最优解。
上篇博客介绍了边缘模型以及基本的边缘检测算法,接下来将了解Canny算法的步骤:
1. 使用高斯函数滤波器平滑输入图像
令f(x,y)表示输入图像,G(x,y)表示高斯函数:
![]()
我们用G和f卷积后得到平滑后的图像fs(x,y):
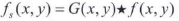
Mat gauImg; GaussianBlur(src, gauImg, Size(13, 13), 2);
2. 计算梯度幅度和角度图像
计算梯度:
![]()
分别计算梯度幅度M的方向α:
![]()
![]() 代码实现:
代码实现:
Mat grad_x, grad_y, grad_xy; Sobel(gauImg, grad_x, CV_32F, 1, 0, 3); Sobel(gauImg, grad_y, CV_32F, 0, 1, 3); Mat directImg, gradXY; divide(grad_y, grad_x, directImg); Mat gradX, gradY; convertScaleAbs(grad_x, gradX); convertScaleAbs(grad_y, gradY); gradXY = gradX + gradY;
3. 非极大值抑制
利用非极大值抑制,细化梯度图像在局部极大值附近包含的一些宽脊。这种方法的实质是规定法线(梯度向量)的多个离散方向。例如,在一个3×3区域内,对于一个过该区域中心点的边缘,我们可以定义4个方向:水平,垂直,+45度和-45度,分别为d1,d2,d3,d4。对于任意点(x,y)为中心的3×3区域,我们将非极大值抑制方案表述如下:
1. 寻找最接近α(x,y)的方向dk。
2. 令K表示梯度幅值在(x,y)处的值。若K小于dk方向上的点(x,y)的一个或两个邻点处的幅度值,令g(x,y)=0(抑制);否则,令g(x,y)=K。
对x和y的所有值重复这一过程,产生一幅与梯度幅值图像大小相同的非极大值抑制图像g(x,y)。例如下图的边缘点,方向均是垂直方向,感兴趣的点为p2和p8,如果p5大于等于这两点,则保留该点,不然令该点为0(抑制)。
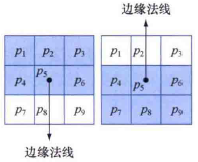
代码实现:将梯度法线分为4个方向,根据4个方向找相邻感兴趣的两个点的梯度幅值
void NMS(Mat& grad_x, Mat& grad_y,Mat& gradXY, Mat& directImg, Mat& dst) {
dst = gradXY.clone();
for (int i = 1; i < grad_x.rows - 1; i++) {
for (int j = 1; j < grad_x.cols - 1; j++) {
directImg.at<float>(i, j) = atan(directImg.at<float>(i, j));
int P1 = (int)gradXY.at<uchar>(i - 1, j - 1);
int P2 = (int)gradXY.at<uchar>(i - 1, j);
int P3 = (int)gradXY.at<uchar>(i - 1, j + 1);
int P4 = (int)gradXY.at<uchar>(i, j - 1);
int P5 = (int)gradXY.at<uchar>(i, j);
int P6 = (int)gradXY.at<uchar>(i, j + 1);
int P7 = (int)gradXY.at<uchar>(i + 1, j - 1);
int P8 = (int)gradXY.at<uchar>(i + 1, j);
int P9 = (int)gradXY.at<uchar>(i + 1, j + 1);
// 边缘法线水平 —
if (directImg.at<float>(i, j) <= CV_PI / 8 && directImg.at<float>(i, j) >= -CV_PI / 8)
if (P5 < P4 || P5 < P6)
dst.at<uchar>(i, j) = 0;
// 边缘法线45° \
if (directImg.at<float>(i, j) > CV_PI / 8 && directImg.at<float>(i, j) < CV_PI / 8 * 3)
if (P5 < P1 || P5 < P9)
dst.at<uchar>(i, j) = 0;
// 边缘法线垂直 |
if ((directImg.at<float>(i, j) >= CV_PI / 8 * 3 && directImg.at<float>(i, j) <= CV_PI / 2) ||
(directImg.at<float>(i, j) <= -CV_PI / 8 * 3 && directImg.at<float>(i, j) >= -CV_PI / 2))
if (P5 < P2 || P5 < P8)
dst.at<uchar>(i, j) = 0;
// 边缘法线-45° /
if (directImg.at<float>(i, j) < -CV_PI / 8 && directImg.at<float>(i, j) > -CV_PI / 8 * 3)
if (P5 < P3 || P5 < P7)
dst.at<uchar>(i, j) = 0;
}
}
}
通常为了更加精确的计算,在跨梯度方向的两个相邻像素之间使用线性插值来得到要比较的像素梯度。在讨论时分为下面4种情况:
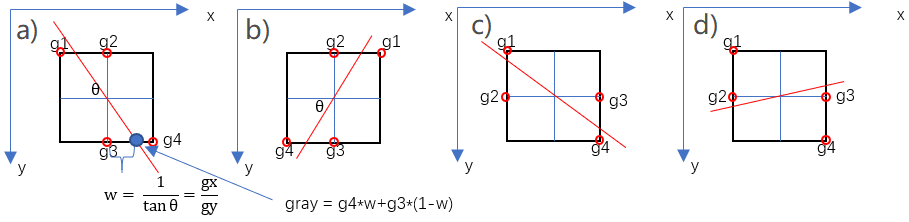
代码实现:线性插值计算感兴趣两点的梯度幅值
void NMS(Mat& grad_x, Mat& grad_y, Mat& gradXY, Mat& dst) {
dst = gradXY.clone();
for (int i = 1; i < grad_x.rows - 1; i++) {
for (int j = 1; j < grad_x.cols - 1; j++) {
float gx = grad_x.at<float>(i, j);
float gy = grad_y.at<float>(i, j);
int g1, g2, g3, g4; float w;
if (abs(gy) > abs(gx)){
g2 = gradXY.at<uchar>(i - 1, j);
g3 = gradXY.at<uchar>(i + 1, j);
w = abs(gx / gy);
if (gx * gy > 0) {
g1= gradXY.at<uchar>(i - 1, j - 1);
g4 = gradXY.at<uchar>(i + 1, j + 1);
}
else {
g1 = gradXY.at<uchar>(i - 1, j + 1);
g4 = gradXY.at<uchar>(i + 1, j - 1);
}
}
else {
g2 = gradXY.at<uchar>(i, j - 1);
g3 = gradXY.at<uchar>(i, j + 1);
w = abs(gy / gx);
if (gx * gy > 0) {
g1 = gradXY.at<uchar>(i - 1, j - 1);
g4 = gradXY.at<uchar>(i + 1, j + 1);
}
else {
g1 = gradXY.at<uchar>(i + 1, j - 1);
g4 = gradXY.at<uchar>(i - 1, j + 1);
}
}
float grad1 = g1 * w + g2 * (1 - w);
float grad2 = g4 * w + g3 * (1 - w);
if (gradXY.at<uchar>(i, j) < grad1 || gradXY.at<uchar>(i, j) < grad2)
dst.at<uchar>(i, j) = 0;
}
}
}
4. 使用双阈值处理和连通性分析来检测和连接边缘
双阈值处理是指设置两个阀值,分别为TL和TH。其中大于TH的都被检测为边缘,而低于TL的都被检测为非边缘。对于中间的像素点,如果与确定为边缘的像素点邻接,则判定为边缘;否则为非边缘。具体地说,高阈值得到的图像gH为强边缘,低阈值得到图像gL的弱边缘。强边缘均被认为是有效边缘,并被立即标记。较长的边缘容易被高阈值切断,可利用下面的步骤连接较长的边缘:
(a)在gH中定位下一个未被访问的边缘像素p;
(b)将gL(x,y)中中用8连通连接到p的所有若像素标记为有效边缘像素
(c)如果gH中的所有非零像素已被访问,则跳到步骤(d),否则返回步骤(a)
(d)将gL中未标记为有效边缘像素的所有像素设置为零
在这一过程的末尾,将来自gL(x,y)的所有非零像素附加到gH(x,y),形成canny算子输出的最终图像。
代码实现:利用了膨胀重建完成上面的过程
以gH为标记图,gL为模板,进行膨胀重建,若想了解形态学重建,移步链接
//膨胀重建
void dilateRestruct(Mat& mark, Mat& mould, Size dilate_size, Mat& dst) {
Mat dilateImg_pre = mark.clone();
Mat temp = mark.clone();
Mat cmp = Mat::zeros(mould.size(), CV_8UC1);
Mat element = getStructuringElement(MORPH_RECT, dilate_size);
int n = -1;
while (n != mould.cols * mould.rows) {
morphologyEx(dilateImg_pre, temp, MORPH_DILATE, element);
bitwise_and(temp, mould, temp);
compare(temp, dilateImg_pre, cmp, 0);
n = countNonZero(cmp);
dilateImg_pre = temp.clone();
}
dst = temp;
}
//双阈值
void double_threshold(Mat& src, int T_low, int T_high, Mat& dst) {
Mat g_h, g_l, g;
threshold(src, g_h, 65, 255, THRESH_BINARY);
threshold(src, g_l, 25, 255, THRESH_BINARY);
dilateRestruct(g_h, g_l, Size(3, 3), dst);
}
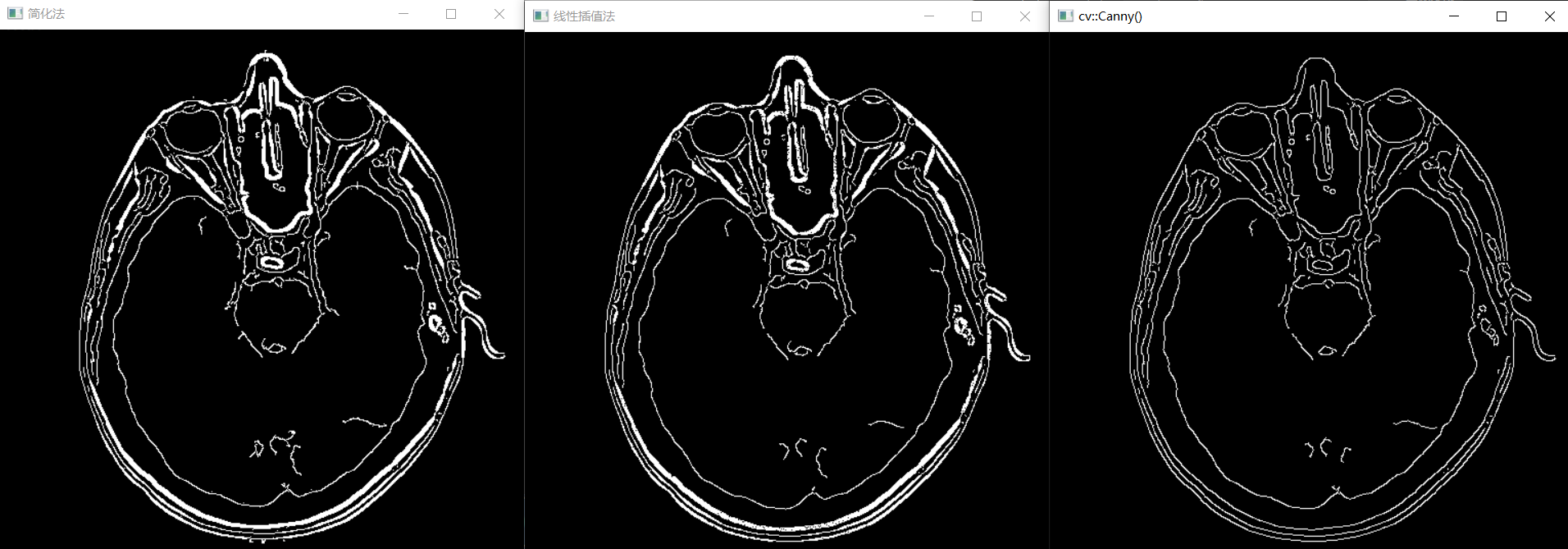
尽管非极大值抑制后的边缘要比原始梯度边缘细,但仍要粗于1像素。为得到1像素粗的边缘,通常要在步骤4后执行一次边缘细化算法(细化见链接)。
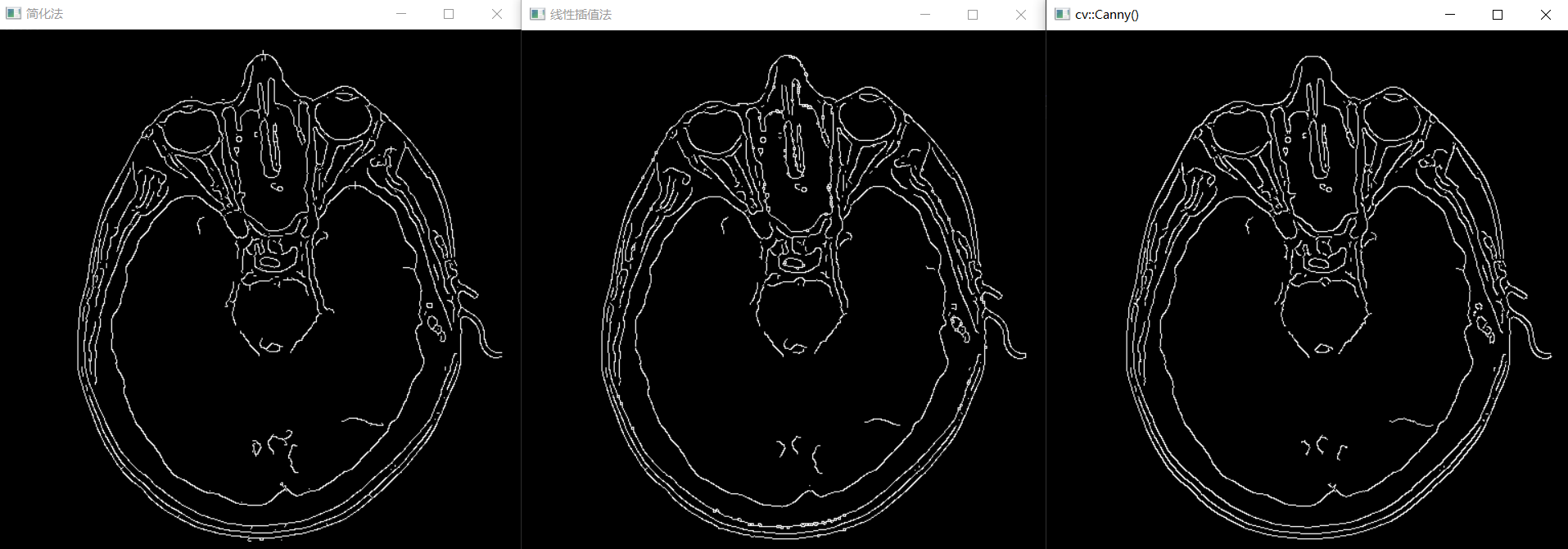
完整代码见链接
参考:
1. 冈萨雷斯《数字图像处理(第四版)》Chapter 10 (所有图片可在链接中下载)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号