【图像处理笔记】灰度级形态学

形态学图像处理是指，以数学形态学为工具从图像中提取表达和描绘区域形状的有用图像分量，如边界、骨架和凸壳等，以及预处理或后处理的形态学技术，如形态学滤波、细化和修剪等。形态学运算时用集合来定义的。在图像处理中，我们使用两类像素集合的形态学：目标元素和结构元（SE）。通常，目标定义为前景像素元素集合。结构元可以按照前景像素和背景像素来规定。此外，结构元有时会包含所谓的“不关心”元素，这意味着SE中这个特定元素的值无关紧要。

1 工具

本节首先把膨胀、腐蚀、开运算和闭运算的基本运算拓展到灰度图像。在接下来的讨论中，我们处理的是形如f(x,y)和b(x,y)的数字函数，其中f(x,y)是一幅灰度图像，b(x,y)是一个结构元。结构元是检查给定图像中特定特性的“探测器”。灰度级形态学中的结构元分为两类：非平坦结构元和平坦结构元，平坦结构元是指灰度剖面平坦，实际工作中很少使用灰度非平坦结构元，因此本节中的所有例子都基于单位高度的、对称的、平坦的、原点位于中心的结构元。

1.1 灰度腐蚀和膨胀

当平坦结构元b的原点是(x,y)时，它在(x,y)处对图像f的灰度腐蚀定义为，图像f与b重合区域中的最小值。结构元b在位置(x,y)处对图像f的腐蚀写为：

类似地，当b的反射的原点是(x,y)时，平坦结构元b在(x,y)处对图像f的膨胀，定义为图像f与b的反射重合区域中的最大值，即

示例：灰度X射线图像分别使用半径为2像素的圆形结构元腐蚀、膨胀图像

Mat src = imread("./7.png", 0);
Mat erodeImg, dilateImg;
Mat element = getStructuringElement(MORPH_ELLIPSE, Size(4, 4));
morphologyEx(src, erodeImg, MORPH_ERODE, element);
Mat element1 = getStructuringElement(MORPH_ELLIPSE, Size(4, 4));
morphologyEx(src, dilateImg, MORPH_DILATE, element1);

我们通常认为腐蚀后的灰度图像要比原图像暗，并且亮特征（相对于SE的大小）变小，暗特征变大。比如在上图中，erodeImg中小亮点的灰度已降低到看不见的程度，而深色特征变得更宽，背景变得略深。而dilateImg中，亮特征变大，暗特征变小，细黑线快看不见了，背景变得稍亮。

1.2 灰度开运算和闭运算

灰度图像开运算和闭运算的公式，形式上与二值图像开运算和闭运算的公式相同。结构元b对图像f的开运算是

开运算照例首先用b腐蚀f然后用b膨胀得到结果。类似地，b对f的闭运算是

 示例：灰度X射线图像分别使用a）半径为3像素的圆形结构元进行开运算，b）使用半径为5像素的结构元进行闭运算

Mat src = imread("./7.png", 0);
Mat openImg, closeImg;
Mat element = getStructuringElement(MORPH_ELLIPSE, Size(6, 6));
morphologyEx(src, openImg, MORPH_OPEN, element);
Mat element1 = getStructuringElement(MORPH_ELLIPSE, Size(10, 10));

 

openImg是使用半径为3的结构元做开运算得到的，不出所料，所有的亮特征都变小了，变小的程度取决于这些特征相对于结构元的大小。与腐蚀不同的是，开运算对图像中暗特征和背景的影响可以忽略不计。闭运算要去除比小亮点更大的小黑点，则需要更大的结构元。在closeImg中，亮细节和背景相对来说未受影响，但削弱了暗特征，削弱的程度取决于这些特征相对于结构元的大小。

2 灰度图像形态学算法

2.1 形态学平滑

由于开运算抑制比规定结构元小的亮细节，同时机会不影响暗细节，而闭运算的效果相反，因此我们通常组合使用这两种运算来平滑图像和去除噪声。

示例：天鹅星座环超新星图像使用半径为5像素的圆形结构元进行开运算+闭运算

Mat src = imread("./8.png", 0);
Mat openImg, closeImg;
Mat element = getStructuringElement(MORPH_ELLIPSE, Size(5, 5));
morphologyEx(src, openImg, MORPH_OPEN, element);
Mat element1 = getStructuringElement(MORPH_ELLIPSE, Size(5, 5));
morphologyEx(openImg, closeImg, MORPH_CLOSE, element1);

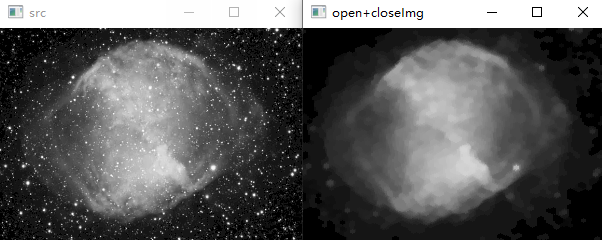
 2.2 形态学梯度

膨胀和腐蚀结合图像相减，可以得到灰度图像f的形态学梯度g，它定义为

使用这一公式得到的总体效果是，膨胀粗化图像中的区域，腐蚀收缩图像中的区域。膨胀腐蚀的差强调区域之间的边界。同质区域不受影响，因此相减运算会消除同质区域。最终结果是，边缘得到增强、同质区域的贡献得到抑制，进而产生“类导数”’（梯度）的效果。

示例：脑部CT图像膨胀和腐蚀结合图像相减

Mat src = imread("./9.png", 0);
Mat erodeImg, dilateImg;
Mat element = getStructuringElement(MORPH_ELLIPSE, Size(4, 4));
morphologyEx(src, erodeImg, MORPH_ERODE, element);
Mat element1 = getStructuringElement(MORPH_ELLIPSE, Size(4, 4));
morphologyEx(src, dilateImg, MORPH_DILATE, element1);
Mat sub = dilateImg - erodeImg;

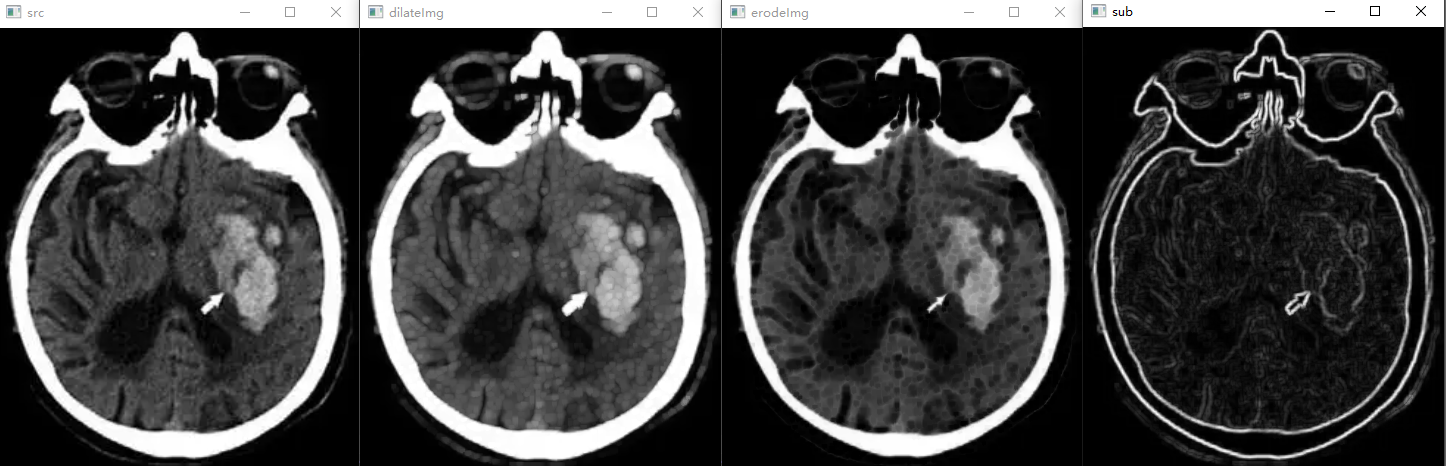
2.3 顶帽变换和底帽变换

图像相减结合开运算和闭运算，可以得到所谓的顶帽变换和底帽变换。灰度图像f的顶帽变换定义为f减去其开运算：

类似地，f的底帽变换定义为f的闭运算减去f：

这些变换的主要应用之一是，在开运算或闭运算中用一个结构元从图像中删除目标，而不是拟合将被删除的目标。然后，差运算得到一幅仅保留已删除分量的图像。顶帽变换用于暗背景上的亮目标，而底帽变换则用于亮背景上的暗目标。因此我们通常将这两个变换称为白顶帽变换和黑底帽变换。

示例：使用顶帽变换校正阴影

Mat src = imread("./10.png", 0);
Mat binImg, tophatImg, blackhatImg, dst;
// 1. Otsu最优阈值处理方法
threshold(src, binImg, 127, 255, THRESH_OTSU);

// 2. 顶帽变换校正阴影后Otsu
Mat element = getStructuringElement(MORPH_CROSS, Size(41, 41));
morphologyEx(src, tophatImg, MORPH_TOPHAT, element);
threshold(tophatImg, dst, 127, 255, THRESH_OTSU);

上面原图为一幅米粒图像，是在非均匀光照下得到的，图像底部和最右侧的暗色区域非常明显。中间图是用Otsu最优阈值处理方法得到的结果，由于非均匀光照，暗区域的分割出现了错误，有些米粒未从背景中提取出来（右下角），同时有些背景被当做了米粒（左上角）。右图中做了顶帽变换（先开运算删除目标得到背景图，再用原图减去背景图），背景变得很均匀，再做阈值分割提取所有米粒。

2.4 粒度测定

粒度测定是指确定图像中颗粒的大小分布。由于颗粒急剧无法整齐的分开，因此采用逐个识别颗粒的方法来计算颗粒的属两个非常困难。形态学可间接估计颗粒的大小分布，而不需要识别和测量各个颗粒。对于比背景亮且形状规则的颗粒，这种方法是用逐渐增大的结构元对图像进行开运算。基本思想是，某个特殊大小的开运算会对包含类似大小颗粒的输入图像的那些区域产生最大影响。对于开运算得到的每幅图像，我们计算像素之和。这个和值称为表面区域，它随结构元的增大而减小，因为开运算会减小图像的亮特征。这一过程得到一个一维阵列，阵列中的每个元素都是对应大小的结构元开运算后的像素之和。为了强调两个连续开运算之间的变化，我们计算一维阵列中相邻两个元素的差。画出差值的图像，曲线中的峰值就会指明图像中主要大小颗粒的分布。

示例：使用开运算进行粒度测定

Mat src = imread("./11.png", 0);
Mat openImg, dst;
int tempGray = sum(src)[0];
for (size_t i = 1; i < 36; i=i+2)
{
    Mat element = getStructuringElement(MORPH_ELLIPSE, Size(i, i));
    morphologyEx(src, openImg, MORPH_OPEN, element);
    int sumGray = sum(openImg)[0];
    int d = tempGray - sumGray;
    cout << d << endl;
    tempGray = sumGray;
    if (i%10==5)
        imshow("openImg(ksize="+to_string(i)+")", openImg);
}

  

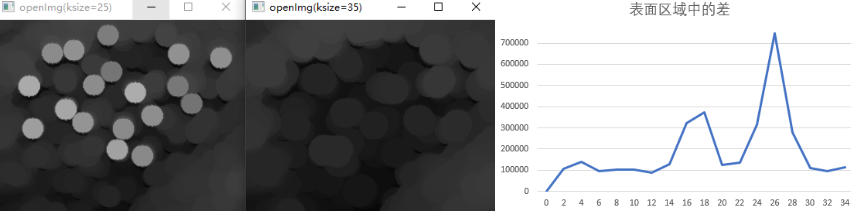
2.5 纹理分割

　　形态学的纹理分割是以纹理内容为基础，找到两个区域的边界，将图像分割为不同的区域。下图是一幅在亮背景上叠加了暗斑点的噪声图像。图像有两个纹理区域，左侧区域包括一些较小的斑点，而右侧区域包括一些较大的斑点。由于目标斑点比背景暗，可以用一个尺寸大于较小斑点的圆形结构元对图像进行闭运算，删除较小的斑点，就得到只有大斑点的图像。再用尺寸大于较大斑点的圆形结构元对图像进行开运算，可以删除较大斑点之间的亮间距，整个图像形成左侧亮色和右侧暗色两个区域。通过形态学梯度运算，就得到两个区域的边界。最后将形态学梯度获得的边界叠加到原图像上，就实现了左右两种不同纹理的区域分割。

示例：纹理分割

Mat src = imread("./12.png", 0);
Mat closeImg, dst, openImg, gradImg;
Mat element = getStructuringElement(MORPH_ELLIPSE, Size(19, 19));
morphologyEx(src, closeImg, MORPH_CLOSE, element);
Mat element1 = getStructuringElement(MORPH_ELLIPSE, Size(61, 61));
morphologyEx(closeImg, openImg, MORPH_OPEN, element1);
Mat element2 = getStructuringElement(MORPH_RECT, Size(3, 3));
morphologyEx(openImg, gradImg, MORPH_GRADIENT, element2);
bitwise_or(gradImg, src, dst);

 

 

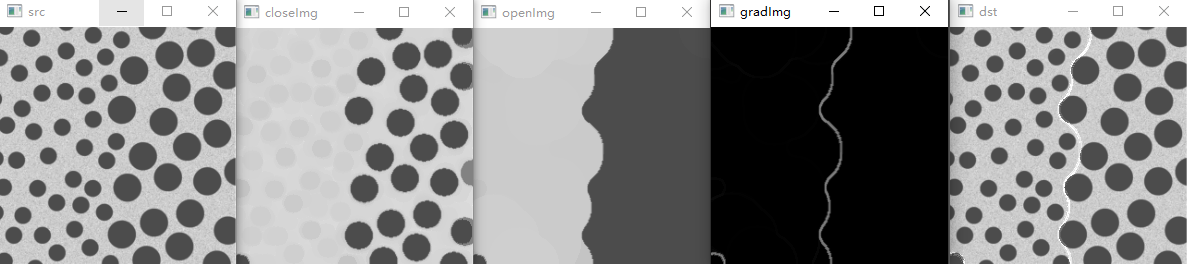
参考：

1. 冈萨雷斯《数字图像处理（第四版）》Chapter 9 （所有图片可在链接中下载）