【图像处理笔记】二值图像形态学

　　形态学图像处理是指，以数学形态学为工具从图像中提取表达和描绘区域形状的有用图像分量，如边界、骨架和凸壳等，以及预处理或后处理的形态学技术，如形态学滤波、细化和修剪等。形态学运算时用集合来定义的。在图像处理中，我们使用两类像素集合的形态学：目标元素和结构元（SE）。通常，目标定义为前景像素元素集合。结构元可以按照前景像素和背景像素来规定。此外，结构元有时会包含所谓的“不关心”元素，这意味着SE中这个特定元素的值无关紧要。

1 工具

1.1 腐蚀

前景像素的集合A，结构元B对A的腐蚀定义为

 式中，z是前景像素值。换句话说，这个公式指出B对A的腐蚀是所有点z的集合，条件是平移z后的B包含于A。

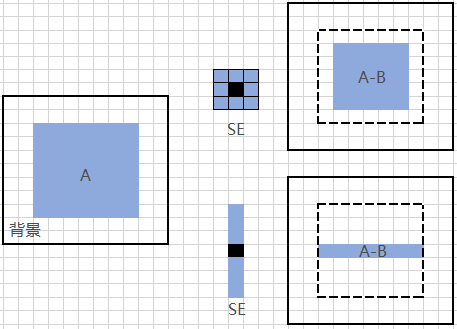
下图显示了腐蚀的一个例子。集合A（显示为蓝色）的元素是图像的前景像素，背景显示为白色。中间为两个不同的结构元SE，右边为（结构元所有元素都完全包含于A的）结构元原点的所有位移位置，即结构元对A的腐蚀。

opencv函数

void dilate //erode
(
    InputArray src,                    //输入源图像
    OutputArray dst,                   //目标图像，需要和源图像有一样的尺寸和类型
    InputArray kernel,                 //膨胀/腐蚀操作的核。当此值为NULL时，表示的是使用参考点位于中心3*3的核
    Point anchor = Point(-1, -1),      //Point类型的anchor，锚的位置，其有默认值（-1，-1），表示锚位于中心
    int iterations=1,                  //表示dilate的次数，默认值为1
    int borderType = BORDER_CONSTANT,  //用于推断图像外部像素某种边界模式，默认值为BORDER_DEFAULT
)

其中，kernel可以通过getStructuringElement函数获得，该函数会返回指定形状和尺寸的结构元素。一般在调用erode以及dilate函数之前，先定义一个Mat类型的变量来获得getStructuringElement函数的返回值。

Mat getStructuringElement(
　　int shape,                  //内核形状，有三种形状可以选择，MORPH_RECT（矩形）；MORPH_CROSS（交叉形）；MORPH_ELLIPSE（椭圆形）
　　Size esize,                 //内核的尺寸
　　Point anchor = Point(-1, -1)//锚点的位置
);

示例：

void onChangeTrackBar(int pos, void* userdata)
{
    Mat src = *(Mat*)(userdata);
    Mat dst;
    Mat element = getStructuringElement(MORPH_RECT, Size(pos, pos));
    erode(src, dst, element);
    imshow("erode", dst);
}
int main(){
    int pos = 0;
    int max_value = 20;
    Mat img;
    img = imread("./1.tif");
    if (img.empty()) return -1;
    namedWindow("erode", WINDOW_AUTOSIZE);
    imshow("erode", img);
    createTrackbar("pos", "erode", &pos, max_value, onChangeTrackBar,&img);
    waitKey();
    return 0;
}

1.2 膨胀

结构元B对集合A的膨胀定义为

B对A的膨胀是所有位移z的集合，条件是B相对于其原点反射后的前景元素与A的至少一个元素重叠。膨胀腐蚀类似于空间卷积，会逐步滑过集合A。但是膨胀腐蚀是以集合运算为基础的，是非线性运算；而卷积是乘积求和，是线性运算。

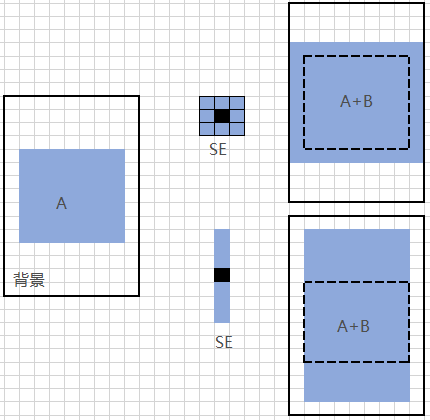
腐蚀是一种收缩或细化运算，而膨胀会“增长”或“粗化”二值图像中的目标。粗化的方式和宽度受所用结构元的大小和形状控制。

Opencv函数：

void dilate( InputArray src, OutputArray dst, InputArray kernel,
                          Point anchor = Point(-1,-1), int iterations = 1,
                          int borderType = BORDER_CONSTANT,
                          const Scalar& borderValue = morphologyDefaultBorderValue()

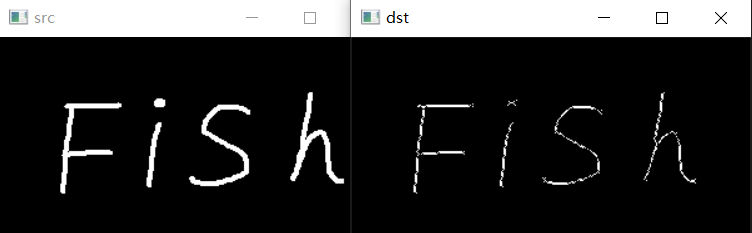
示例：使用膨胀修复图像中的断裂文字

Mat src = imread("./1.png");
Mat element = getStructuringElement(MORPH_RECT, Size(3,3));
Mat dst;
morphologyEx(src, dst, MORPH_DILATE, element);

1.3 开运算与闭运算

　　开运算通常平滑物体的轮廓、断开狭窄的狭颈、消除细长的突出物；闭运算同样平滑轮廓，但与开运算相反，它通常弥合狭窄的断裂和细长的沟壑，消除小孔，并填补轮廓中的缝隙。

结构元B对集合A的开运算定义为，首先B对A腐蚀，接着B对腐蚀结果膨胀：

 

类似的，结构元B对集合A的闭运算定义为，首先B对A膨胀，接着B对膨胀结果腐蚀：

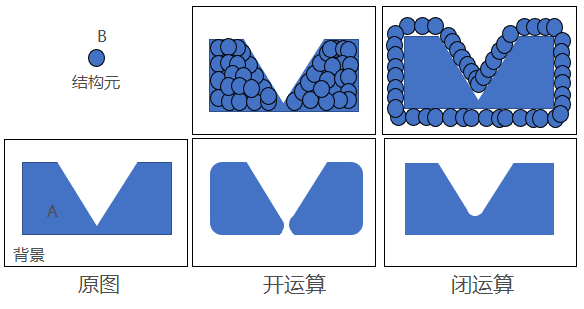
下图是包含一个集合（目标）A的图像，B是一个实心的圆形结构元。可以看出，B对A的开运算是B所有平移的并集，由于B不能拟合A中心位置的狭窄段，所以开运算是由两个不相交的子集组成的集合。闭运算是B的所有不与A重叠的平移的补集。

 示例： 使用开运算和闭运算进行形态学滤波

1.4 击中-击不中变换

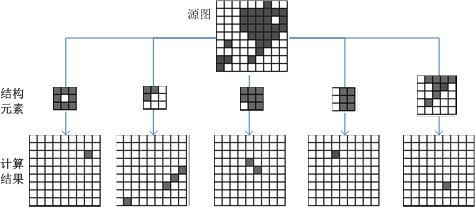
　　形态学击中-击不中变换（HMT）是形状检测的基本工具，常用于二值图像，通过定义一定形状的结构元素，然后在图像中寻找与该结构元素相同的区域，找到即为击中，找不到即为击不中。即在图像A中，找B（结构元structuring element）并输出其原点（origin）。

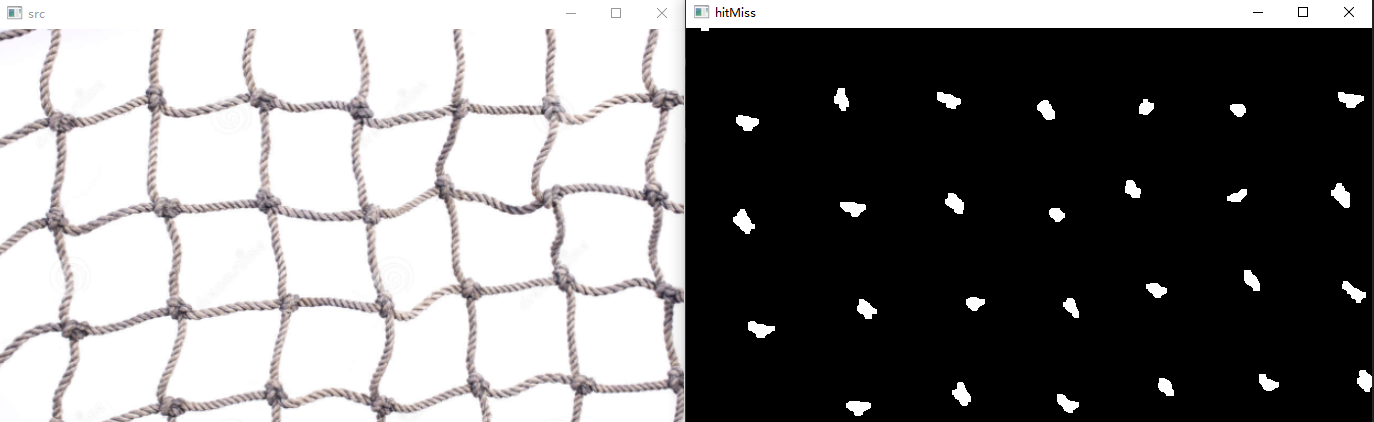
示例：找到绳子打结处

Mat src = imread("./3.png");
Mat gray, gauss, binary, hitImg, openImg;
cvtColor(src, gray, COLOR_BGR2GRAY);
GaussianBlur(gray, gauss, Size(5, 5), 0, 0);
threshold(gauss, binary, 0, 255, THRESH_BINARY_INV | THRESH_OTSU);
Mat kern = getStructuringElement(MORPH_CROSS, Size(11, 11));
morphologyEx(binary, hitImg, MORPH_HITMISS, kern);
Mat kern2 = getStructuringElement(MORPH_RECT, Size(3, 3));
morphologyEx(hitImg, openImg, MORPH_OPEN, kern2, Point(-1, -1), 2);

2 二值图像形态学算法

2.1 边界提取

前景像素集合A的边界ß(A)可按如下方式得到：首先使用合适的结构元B腐蚀A，然后求A和腐蚀结果的差集。也就是说，

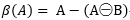示例：边界提取

Mat src = imread("./4.png",0);
Mat thr, dst, ero;
threshold(src, thr, 128, 255, THRESH_BINARY);
Mat kernel = getStructuringElement(MORPH_RECT, Size(3, 3));
morphologyEx(thr, ero, MORPH_ERODE, kernel);
subtract(thr, ero, dst);

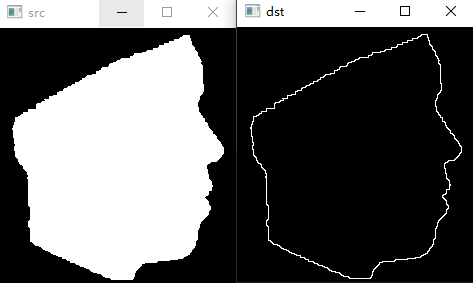
2.2 孔洞填充

　　孔洞是被前景像素连成的边框所包围的背景区域。本节将为图像中的空洞填充开发一个算法，这个算法是以集合膨胀、补集和交集为基础的。令A表示一个集合，其元素时8连通的边界，每个边界包围一个背景区域（及一个孔洞）。当给定每个孔洞中的一点后，目的就是用1填充所有的孔洞。公式为：

其中B表示对称结构元（以下将以 3×3 十字形结构元为例展开说明），I表示包含A的图像，Ic表示原图像的补集。每一步中与 Ic的交集操作，是将膨胀结果控制在感兴趣的范围内​​​，如果 Xk=Xk−1，则算法在迭代的第k步结束。然后，集合Xk包含所有被填充的孔洞，最终取集合Xk和A的并集即完成了该图像各个孔洞的填充任务。

但上述方法仅在已知孔洞中任意一点时使用，当该点未知，且孔洞数目较多时，这种方法的实用性较低。那么，有没有一种可以自动进行孔洞填充，无需知道任意孔洞的位置？

首先，一个孔洞可以被定义为由前景像素相连的边界所包围的一个背景区域，那么，该孔洞的边界，是连通的。利用这一点，对于一张图像I，找到边界中的任意一点，对该点进行膨胀，膨胀结果与Ic作交集（如此，遇到闭合区域不会膨胀进去），再对该交集结果作膨胀，再作交集，以此类推，直至所得的集合不再变化。

Mat I = imread("./2.png",0);
threshold(I, I, 128, 255, THRESH_BINARY);
Mat Ic,thr, dst, tmp, dilImg;
bitwise_not(I, Ic);
Mat mask = Mat::zeros(I.size(), CV_8UC1);
tmp = mask.clone();
mask.at<uchar>(0, 0) = 255;
Mat kernel = getStructuringElement(MORPH_CROSS, Size(3, 3));
int diff = -1;
while (diff!=0) {
    tmp = mask.clone();
    morphologyEx(mask, dilImg, MORPH_DILATE, kernel);
    bitwise_and(dilImg, Ic, mask);
    diff = sum(mask - tmp)[0];
}
bitwise_not(mask, dst);

泛洪算法——Flood Fill，（也称为种子填充——Seed Fill）是一种算法，用于确定连接到多维数组中给定节点的区域。 它被用在油漆程序的“桶”填充工具中，用于填充具有不同颜色的连接的，颜色相似的区域，并且在诸如围棋（Go）和扫雷（Minesweeper）之类的游戏中用于确定哪些块被清除。泛洪算法的基本原理就是从一个像素点出发，以此向周边的像素点扩充着色，直到图形的边界。在OpenCV中，漫水填充是填充算法中最通用的方法。

示例：漫水填充cv::floodFill()

Mat I = imread("./2.png",0);
threshold(I, I, 128, 255, THRESH_BINARY);
Mat dst;
Mat mask = I.clone();
floodFill(mask, Point(0, 0), 255);
bitwise_not(mask, mask);
dst = mask + I;

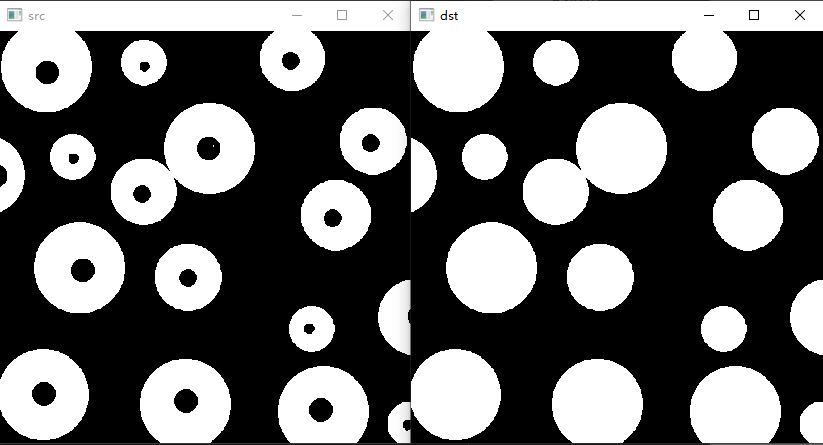
2.3 提取连通分量

　　从二值图像中提取连通分量是自动图像分析的核心步骤。冈萨雷斯《数字图像处理（第四版）》提供了一种提取连通分量的形态学算法，构造一个元素为0的阵列X0，其中对应连通分量的像素值为1，采用迭代过程可以得到所有的连通分量：

该算法与约束膨胀孔洞填充的思路相同，使用条件膨胀来限制膨胀的增长，但用I代替Ic以寻找前景点。

　　对于内含多个连通分量的图像A，从仅为连通分量A1内部的某个像素B开始，用3*3的结构元不断进行膨胀。由于其它连通分量与A1之间至少有一条像素宽度的空隙，每次膨胀都不会产生位于其它连通区域内的点。用每次膨胀后的图像与原始图像A取交集，就把膨胀限制在A1内部。随着集合B的不断膨胀，B的区域不断生长，但又被限制在连通分量A1的内部，最终就会充满整个连通分量A1，从而实现对连通分量A1的提取。

Mat dilImg, tmp1, sub, I;
Mat src = imread("./5.png",0);
threshold(src, I, 200, 255, THRESH_BINARY);
Mat tmp = I.clone();
Mat markImg = Mat::zeros(I.size(), CV_8UC3);
Mat mask = Mat::zeros(I.size(), CV_8UC1);
Mat kernel = getStructuringElement(MORPH_RECT, Size(3, 3));
vector<vector<Point>> cons;
while (countNonZero(tmp) != 0) {
    vector<Point> idx;
    findNonZero(tmp, idx);
    mask.at<uchar>(idx[0].y, idx[0].x) = 255;
    tmp1 = mask.clone();
    sub = mask.clone();
    while (countNonZero(sub) != 0)
    {
        morphologyEx(mask, dilImg, MORPH_DILATE, kernel);
        bitwise_and(dilImg, I, mask);
        sub = mask - tmp1;    
        tmp1 = mask.clone();
     }
     tmp -= mask;
}

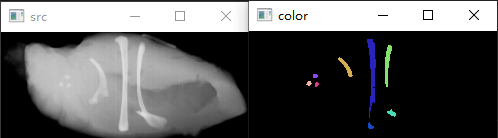
　　提取连通分量的过程也是对连通分量的标注，通常给图像中的每个连通区分配编号，在输出图像中该连通区内的所有的像素值赋值为对应的区域编号，这样的输出图像被称为标注图像。在opencv中，函数cv::connectedComponents()以及cv::connectedComponentsWithStats()都创建了这样的标记图。根据标记图，可以使不同区域有不同的颜色。

示例：cv::connectedComponentsWithStats()

#include <opencv2/opencv.hpp>
#include <algorithm>
#include <iostream>
using namespace std;
int main()
{
    cv::Mat src_img, img_bool, labels, stats, centroids, img_color, img_gray;

    if ((src_img = cv::imread("./5.PNG", 0)).empty())
    {
        cout << "load image error！";
        return -1;
    }
    cv::threshold(src_img, img_bool, 200, 255, cv::THRESH_BINARY);
    //连通域计算
    int nccomps = cv::connectedComponentsWithStats(
        img_bool, //二值图像
        labels,   //和原图一样大的标记图
        stats,    //nccomps×5的矩阵 表示每个连通区域的外接矩形和面积（pixel）
        centroids //nccomps×2的矩阵 表示每个连通区域的质心
    );
    //去除过小区域，初始化颜色表
    vector<cv::Vec3b> colors(nccomps);  ////8U形式的RGB彩色图像，灰度值范围为0~255
    colors[0] = cv::Vec3b(0, 0, 0); // background pixels remain black.
    for (int i = 1; i < nccomps; i++) {
        colors[i] = cv::Vec3b(rand() % 256, rand() % 256, rand() % 256);
        //去除面积小于10的连通域
        if (stats.at<int>(i, cv::CC_STAT_AREA) < 10)
            colors[i] = cv::Vec3b(0, 0, 0); // small regions are painted with black too.
    }
    //按照label值，对不同的连通域进行着色
    img_color = cv::Mat::zeros(src_img.size(), CV_8UC3);
    for (int y = 0; y < img_color.rows; y++)
        for (int x = 0; x < img_color.cols; x++)
        {
            int label = labels.at<int>(y, x);
            CV_Assert(0 <= label && label <= nccomps);
            img_color.at<cv::Vec3b>(y, x) = colors[label];
        }

    //统计降噪后的连通区域
    cv::cvtColor(img_color, img_gray, cv::COLOR_BGR2GRAY);
    cv::threshold(img_gray, img_gray, 1, 255, cv::THRESH_BINARY);
    nccomps = cv::connectedComponentsWithStats(img_gray, labels, stats, centroids);
    cv::imshow("src", src_img);
    cv::imshow("color", img_color);
    cv::waitKey();
    return 0;
}
创建标记图并上色

2.4 凸壳

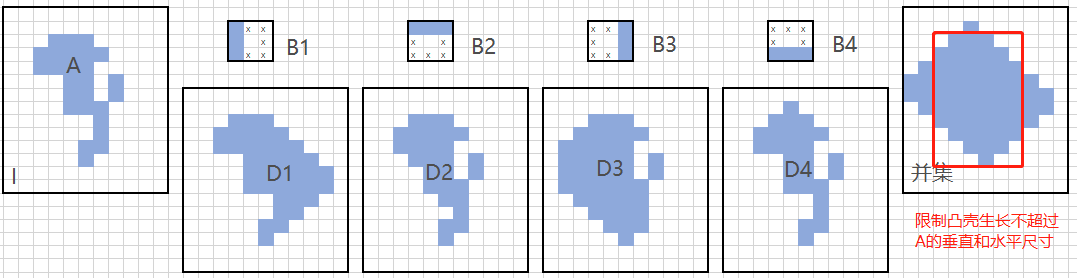
当且仅当数字集合A的欧式凸壳只包含于属于A的数字点，该数字集合A是凸的。一种简单的可视化方法是，用直（连续的）欧几里得线段连接其边界点，如果只有前景点包含于由这些线段形成的集合，那么集合是凸的。令Bi,i=1,2,3,4表示下图中的4个结构元。凸壳程序由如下形态学公式实现：

其中，X0i=I。分别用4个结构元做击中-击不中变换直至收敛，再求并集就是A的凸壳。为了防止凸壳增长到超出保证凸性所需的最小尺寸，设定限制凸壳不超过集合A的垂直和水平尺寸。

cv::ConvexHull()

cv::convexHull(
    InputArray points,      //输入候选点，来自findContours
    OutputArray hull,       //凸包
    Bool clockwise,          //顺时针方向
    Bool returnPoints,      //true表示返回点个数，如果第二个参数是vector<Point>则自动忽略
）

2.5 细化

图像细化（Image Thinning），一般指二值图像的骨架化（Image Skeletonization）的一种操作运算。所谓的细化就是经过一层层的剥离，从原来的图中去掉一些点，但仍要保持原来的形状，直到得到图像的骨架。骨架，可以理解为图象的中轴。

下面为链接中的细化方法

Mat src = imread("./6.png", 0);
Mat edge = src.clone();
Mat element = getStructuringElement(MORPH_CROSS, Size(3, 3));
Mat dst = Mat::zeros(src.size(), CV_8UC1);
Mat openImg, tmp;
int n = -1;
while (countNonZero(edge) != 0) {
    morphologyEx(edge, openImg, MORPH_OPEN, element); // 开运算
    subtract(edge, openImg, tmp); // 获得骨架子集
    bitwise_or(dst, tmp, dst); // 将删除的像素添加到骨架图
    morphologyEx(edge, edge, MORPH_ERODE, element); // 腐蚀，用于下一次迭代
}

 

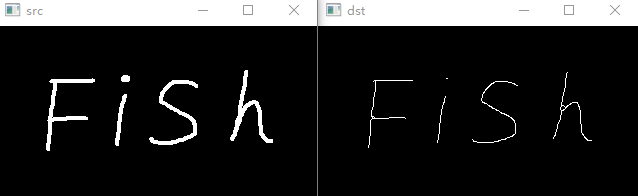
下面是论文 A fast parallel algorithm for thinning digital patterns的细化算法。

第一步：遍历考察所有的非零点，看是否满足以下4个条件：

a. 2<= p2+p3+p4+p5+p6+p7+p8+p9<=6

b. p2->p9的排列顺序中，01模式的数量为1，比如下面的图中，有p2p3 => 01, p6p7=>01,所以该像素01模式的数量为2。之所以要01模式数量为1，是要保证删除当前像素点后的连通性。

c. p2*p4*p6 = 0

d. p4*p6*p8 = 0

将满足以上四个条件的点删除（像素值置为0）

第二步：还是通过四个条件来判断点的去留 

a. 2<= p2+p3+p4+p5+p6+p7+p8+p9<=6

b. p2->p9的排列顺序中，01模式的数量(这里假设二值图非零值为1)为1。

c. p2*p4*p8 = 0

d. p2*p6*p8 = 0

可以看到其实在本质上，两大步骤中四个条件并没有很大的区别，只是在c、d两个条件上变成不同的方向。合并c、d两个条件就可以看到，只需要p2、p4、p6、p8四个像素值有一个为零，中心像素p1就该删除。

opencv实现

#include <opencv2/opencv.hpp>
#include <algorithm>
#include <iostream>
using namespace std;
using namespace cv;

void ThinOnce(Mat& pSrc, Mat& pDst, int flag) {
    int rows = pSrc.rows;
    int cols = pSrc.cols;
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            if (pSrc.at<float>(i, j) == 1.0f) {
                /// get 8 neighbors
                /// calculate C(p)
                int P2 = (int)pSrc.at<float>(i - 1, j);
                int P3 = (int)pSrc.at<float>(i - 1, j + 1);
                int P4 = (int)pSrc.at<float>(i, j + 1);
                int P5 = (int)pSrc.at<float>(i + 1, j + 1);
                int P6 = (int)pSrc.at<float>(i + 1, j);
                int P7 = (int)pSrc.at<float>(i + 1, j - 1);
                int P8 = (int)pSrc.at<float>(i, j - 1);
                int P9 = (int)pSrc.at<float>(i - 1, j - 1);
                int sum = P2 + P3 + P4 + P5 + P6 + P7 + P8 + P9; 
                int arr[9]{ P2, P3, P4, P5, P6, P7, P8, P9, P2 };
                int count = 0;
                for (int i = 0; i < 8; i++) {
                    if (arr[i] == 0 && arr[i + 1] == 1)
                        count++;
                }  
                if (flag == 0 && sum < 7 && sum > 1 && P2 * P4 * P6 == 0 && P4 * P6 * P8 == 0 && count == 1)
                    pDst.at<float>(i, j) = 0.0f;                 
                if (flag == 1 && sum < 7 && sum > 1 && P2 * P4 * P8 == 0 && P2 * P6 * P8 == 0 && count == 1)
                    pDst.at<float>(i, j) = 0.0f; 
            }
        }
    }
}
void thin(Mat& src, Mat& dst) {
    bool bDone = false;
    int rows = src.rows;
    int cols = src.cols;

    /// pad source and dst
    Mat p_enlarged_src, p_enlarged_dst;
    copyMakeBorder(src, p_enlarged_src, 1, 1, 1, 1, BORDER_CONSTANT, Scalar(0));
    p_enlarged_src.convertTo(p_enlarged_src, CV_32F, 1/255.0);
    p_enlarged_dst = p_enlarged_src.clone();

    Mat p_cmp = Mat::zeros(rows + 2, cols + 2, CV_8UC1);
    int iter = 0;
    while (bDone != true) {
        // sub-iteration
        int i = iter % 2; 
        ThinOnce(p_enlarged_src, p_enlarged_dst, i);
        // compare
        compare(p_enlarged_src, p_enlarged_dst, p_cmp, CMP_EQ);
        // check
        int num_non_zero = countNonZero(p_cmp);
        if (num_non_zero == (rows + 2) * (cols + 2)) {
            bDone = true;
        }
        // copy
        p_enlarged_dst.copyTo(p_enlarged_src);
        iter++;
    }
    // copy result
    dst = p_enlarged_dst({ 1, 1, cols, rows }).clone();
}

int main(int argc, char* argv[])
{
    Mat src = imread("./6.png", 0);
    Mat dst;
    thin(src, dst);
    imshow("src", src);
    imshow("dst", dst);
    waitKey(0);
    return 0;
} 

 

 

参考：

1. 冈萨雷斯《数字图像处理（第四版）》Chapter 9 （所有图片可在链接中下载）

2. 形态算法之提取连通分量

posted @ 2022-08-15 21:41  湾仔码农  阅读(1295)  评论(0)  编辑  收藏  举报