Opencv笔记(12)傅里叶变换
在之前了解的OpenCV为我们实现的图像变换,这些本质上是从图像到输出图像的映射,即输入仍是一幅图像。本章的傅里叶变换,输出数组的值在含义上和原图像的强度值大不相同,是输入图像的频域表示。
cv::dft()离散傅里叶变换
dft(InputArray src, // 输入图像,可以是实数或虚数
OutputArray dst, // 输出图像,其大小和类型取决于第三个参数flags
int flags = 0, // 转换的标识符,有默认值0
int nonzeroRows = 0);// 当这个参数不为0,函数会假设只有输入数组(没有设置DFT_INVERSE)的第一行或第一个输出数组(设置了DFT_INVERSE)包含非零值
flag参数
- DFT_INVERSE: 用一维或二维逆变换取代默认的正向变换
- DFT_SCALE: 缩放比例标识符,根据数据元素个数平均求出其缩放结果,如有N个元素,则输出结果以1/N缩放输出,常与DFT_INVERSE搭配使用。
- DFT_ROWS: 对输入矩阵的每一行执行正变换或逆变换;此标志允许您同时变换多个向量,并可用于减少执行3D和更高维度变换等的开销(有时比处理本身大几倍)。
- DFT_COMPLEX_OUTPUT: 对一维或二维的实数数组进行正向变换,这样的结果虽然是复数阵列,但拥有复数的共轭对称性(CCS),可以以一个和原数组尺寸大小相同的实数数组进行填充,这是最快的选择也是函数默认的方法。你可能想要得到一个全尺寸的复数数组(像简单光谱分析等等),通过设置标志位可以使函数生成一个全尺寸的复数输出数组。
- DFT_REAL_OUTPUT: 对一维二维复数数组进行逆向变换,这样的结果通常是一个尺寸相同的复数矩阵,但是如果输入矩阵有复数的共轭对称性(比如是一个带有DFT_COMPLEX_OUTPUT标识符的正变换结果),便会输出实数矩阵。
示例:
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int main() {
clock_t start, end;
start = clock();
int count = 0;
Mat src = imread("F:/wallpaper/1.jpg", 0);
//1. 放大到合适尺寸加速运算
Mat padded;
int opWidth = getOptimalDFTSize(src.cols);
int opHeight = getOptimalDFTSize(src.rows);
copyMakeBorder(src, padded, 0, opHeight - src.rows, 0, opWidth - src.cols, BORDER_REFLECT);
//2. dft 当输入是双通道时,两个通道分别代表实部和虚部
Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(),CV_32F) };
Mat comImg;
merge(planes, 2, comImg);
dft(comImg, comImg, DFT_COMPLEX_OUTPUT);
//3. 分离通道,显示幅值
split(comImg, planes);
Mat magMat;
magnitude(planes[0], planes[1], magMat);
magMat += Scalar::all(1);
log(magMat, magMat);
magMat = magMat(Rect(0, 0, magMat.cols & -2, magMat.rows & -2));
normalize(magMat, magMat, 0, 1, NORM_MINMAX);
//4. 把零频移到中心
Mat magImg(magMat.size(), CV_8UC1);
magMat.convertTo(magImg, CV_8UC1, 255, 0);
magMat = magMat(Rect(0, 0, magMat.cols & -2, magMat.rows & -2));
int cx = magImg.cols / 2;
int cy = magImg.rows / 2;
Mat q1 = magImg({ 0, 0, cx, cy });
Mat q2 = magImg({ 0, cy, cx, cy });
Mat q3 = magImg({ cx, 0, cx, cy });
Mat q4 = magImg({ cx, cy, cx, cy });
Mat temp;
q1.copyTo(temp);
q4.copyTo(q1);
temp.copyTo(q4);
q2.copyTo(temp);
q3.copyTo(q2);
temp.copyTo(q3);
end = clock();
cout << end - start << endl;
return 0;
}

低频信号对应图像内变化缓慢的灰度分量。高频信号对应图像内变化越来越快的灰度分量,是由灰度的尖锐过渡造成的,例如边界。从频谱图上可以看出,当将频谱移频到原点以后,图像中心比较亮。在频谱图中,一个点的亮暗主要与这个频率中点的数目和点的灰度值有关,也就是说在空间域中包含这种频率的点越多。而经过频移后,频率为0的部分,也就是傅里叶变换所得到的常量分量在图像中心,往外扩散,点所代表的频率越来越高。也说明了图像中的“能量”主要集中在低频部分。
cv::idft()离散傅里叶逆变换
dft()不仅可以实现离散傅里叶变换,也可以实现逆变换,dft(src, dst, flags | #DFT_INVERSE) 和idft(src, dst, flags)的效果相等。
void idft(InputArray src, OutputArray dst, int flags = 0, int nonzeroRows = 0);
cv::mulSpectrums()频谱乘法
void mulSpectrums(InputArray a, //输入图像(ccs or complex)
InputArray b, //和a一样为ccs格式单通道频谱or双通道复数频谱
OutputArray c, //目标数组,大小类型与输入一样
int flags, //只支持DFT_ROWS
bool conjB = false);//可选标志,用于决定在乘法操作前是否对第二个输入频谱取共轭。true表示取共轭;false表示不取
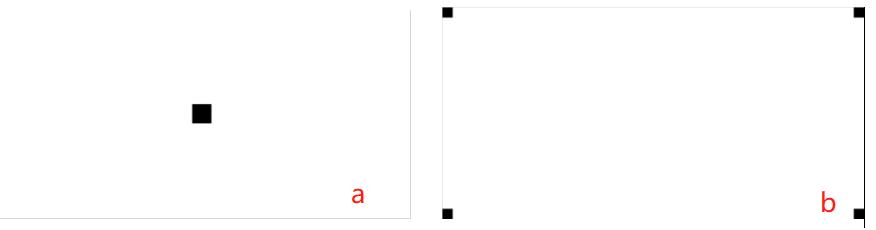
对于将零频移动到中心的频谱图,舍去中心的低频部分,只保留高频,增强图像细节,即用下图a中的mask与频谱图进行频谱乘法。如果没有移动频谱,即用下图b的mask相乘。
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int main() {
clock_t start, end;
start = clock();
int count = 0;
Mat src = imread("F:/wallpaper/1.jpg", 0);
//1. 放大到合适尺寸加速运算
Mat padded;
int opWidth = getOptimalDFTSize(src.cols);
int opHeight = getOptimalDFTSize(src.rows);
copyMakeBorder(src, padded, 0, opHeight - src.rows, 0, opWidth - src.cols, BORDER_REFLECT);
//2. dft 当输入是双通道时,两个通道分别代表实部和虚部
Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(),CV_32F) };
Mat comImg;
merge(planes, 2, comImg);
dft(comImg, comImg, DFT_COMPLEX_OUTPUT);
//3. 保留高频
int d = 100;
Mat mask(opHeight, opWidth, CV_8UC1, Scalar(1));
Rect r1(0, 0, d, d);
Rect r2(0, opHeight - d, d, d);
Rect r3(opWidth - d, 0, d, d);
Rect r4(opWidth-d, opHeight-d, d, d);
mask(r1).setTo(0);
mask(r2).setTo(0);
mask(r3).setTo(0);
mask(r4).setTo(0);
mask.convertTo(mask, CV_32F);
Mat maskImg;
Mat masks[] = { mask,mask };
merge(masks, 2, maskImg);
mulSpectrums(comImg, maskImg, comImg, DFT_ROWS);
//4. 傅里叶反变换
Mat dst;
idft(comImg, comImg, DFT_COMPLEX_OUTPUT);
split(comImg, planes);
magnitude(planes[0], planes[1], dst);
normalize(dst, dst, 0, 1, NORM_MINMAX);
dst.convertTo(dst, CV_8U, 255);
end = clock();
cout << end - start << endl;
return 0;
}
结果:


参考文献:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号