【论文笔记】AlexNet
【深度学习】总目录
由于受到计算机性能的影响,虽然LeNet在图像分类中取得了较好的成绩,但是并没有引起很多的关注。 直到2012年,Alex等人提出的AlexNet网络在ImageNet大赛上以远超第二名的成绩夺冠,卷积神经网络乃至深度学习重新引起了广泛的关注。
论文:《ImageNet Classification with Deep Convolutional Neural Networks》
1. Architecture
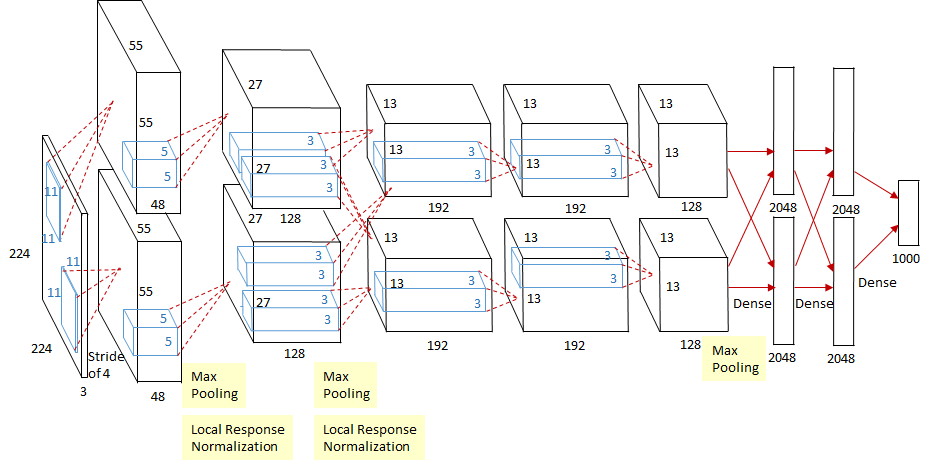
由于当时的GPU运算能力比较低,AlexNet通过两个GPU协同训练,因此文章给出的网络结构不太清晰,参见Netscope。该网络共包含8个权重层,其中5个卷积层,3个全连接层。上面这幅图的feature map维度需要综合上下两个GPU的结果,其输入为224*224*3的图片,第一层卷积层的kernel个数为96,size为11*11*3,步长为4,论文中两片GPU分别计算48个核。由于(224-11)/4 并不能整除,原文应该有误,正确图像尺寸为 227×227×3的图像,平时自己训练取pad=2就好啦。1,2卷积层后连有LRN层,不过此后的网络也证明LRN并非CNN中必须包含的层,甚至有些网络加入LRN后效果反而降低。每个LRN及最后层卷积层后跟有最大池化层,并且各个权重层均连有ReLU激活函数。全连接层后使用了Dropout解决过拟合。
1.1 ReLU Nonlinearity
在最初的感知机模型中,输入和输出的关系:y=Σwixi+b,只是单纯的线性关系。把神经网络看着一个巨大的变换矩阵M,其输入为所有训练样本组成的矩阵B,B=M·A。这样的网络结构有很大的局限性:即使用很多这样结构的网络层叠加,其输出和输入仍然是线性关系,无法处理有非线性关系的输入输出。因此,对每个神经元的输出做个非线性的转换也就是,将上面就加权求和的结果输入到一个非线性函数,也就是激活函数中。这样,由于激活函数的引入,多个网络层的叠加就不再是单纯的线性变换,而是具有更强的表现能力。标准的L-P神经元的输出一般使用tanh或sigmoid作为激活函数,但是这些饱和的非线性函数在计算梯度的时候都要比非饱和的非线性函数ReLUs慢很多。
- sigmoid
在网络层数较少时,sigmoid函数的特性能够很好的满足激活函数的作用:它把一个实数压缩至0到1之间,当输入的数字非常大的时候,结果会接近1;当输入非常大的负数时,则会得到接近0的结果。这种特性,能够很好的模拟神经元在受刺激后,是否被激活向后传递信息(输出为0,几乎不被激活;输出为1,完全被激活)。
sigmoid一个很大的问题就是梯度饱和。 观察sigmoid函数的曲线,当输入的数字较大(或较小)时,其函数值趋于不变,其导数变的非常的小。这样,在层数很多的的网络结构中,进行反向传播时,由于很多个很小的sigmoid导数累成,导致其结果趋于0,权值更新较慢。
- ReLU
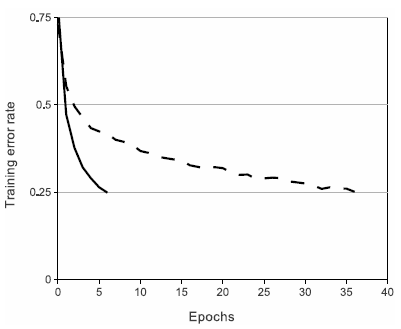
上图是使用ReLUs和tanh作为激活函数的典型四层网络的在数据集CIFAR-10s实验中,error rate达到到0.25时的收敛曲线,可以很明显的看到收敛速度的差距。虚线为tanh,实线是ReLUs。
1.2 Local Response Normalization
AlexNet中首次引入的归一化方法,但是在BatchNorm之后就很少使用这种方法了,所以简单了解下。
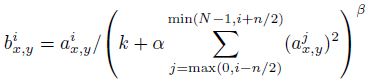
ai(x,y)代表的是ReLU在第i个kernel的(x, y)位置的输出,分母处对前面n/2个通道(最小为第0个通道)和后n/2个通道(最大为第d-1个通道)的对应位置的平方求和(共n+1个点)。k,n,α和β为超参数由验证集决定。一般设置k = 2, n = 5, α = 10-4, and β = 0:75。
1.3 Overlapping Pooling
一般的池化单元是不会重叠的,当移动的步长s小于池化的窗口长度z,这样就会出现重叠。当s=2,z=3,在top-1,和top-5中分别将error rate降低了0.4%和0.3%。同时在训练模型过程中,重叠的池化层更不容易过拟合。
2 Reducing Overfitting
2.1 Data Augmentation
对抗过拟合最简单有效的办法就是扩大训练集的大小,AlexNet中使用了两种增加训练集大小的方式:Image translations & horizontal reflections.对原始的256x256大小的图片随机裁剪为224x224大小,并进行随机翻转,这两种操作相当于把训练集扩大了32x32x2=2048倍。在测试时,AlexNet把输入图片与其水平翻转在四个角处与正中心共五个地方各裁剪下224x224大小的子图,即共裁剪出10个子图,均送入AlexNet中,并把10个softmax输出求平均。如果没有这些操作,AlexNet将出现严重的过拟合,使网络的深度不能达到这么深。AlexNet对RGB通道使用了PCA(主成分分析),对每个训练图片的每个像素,提取出RGB三个通道的特征向量与特征值,对每个特征值乘以一个α,α是一个均值0.1方差服从高斯分布的随机变量。
2.2 Dropout
Dropout是神经网络中一种非常有效的减少过拟合的方法,对每个神经元设置一个keep_prob用来表示这个神经元被保留的概率,如果神经元没被保留,换句话说这个神经元被“dropout”了,那么这个神经元的输出将被设置为0,在残差反向传播时,传播到该神经元的值也为0,因此可以认为神经网络中不存在这个神经元;而在下次迭代中,所有神经元将会根据keep_prob被重新随机dropout。相当于每次迭代,神经网络的拓扑结构都会有所不同,这就会迫使神经网络不会过度依赖某几个神经元或者说某些特征,因此,神经元会被迫去学习更具有鲁棒性的特征。
在AlexNet中,在训练时,每层的keep_prob被设置为0.5,而在测试时,所有的keep_prob都为1.0,也即关闭dropout,并把所有神经元的输出均乘以0.5,保证训练时和测试时输出的均值接近。当然,dropout只用于全连接层。没有dropout,AlexNet网络将会遭遇严重的过拟合,加入dropout后,网络的收敛速度慢了接近一倍。
3 pytorch代码实现
调用pytorch中的torchvision.model.AlexNet,输出其网络架构,如下:
model = torchvision.models.AlexNet() print(model)
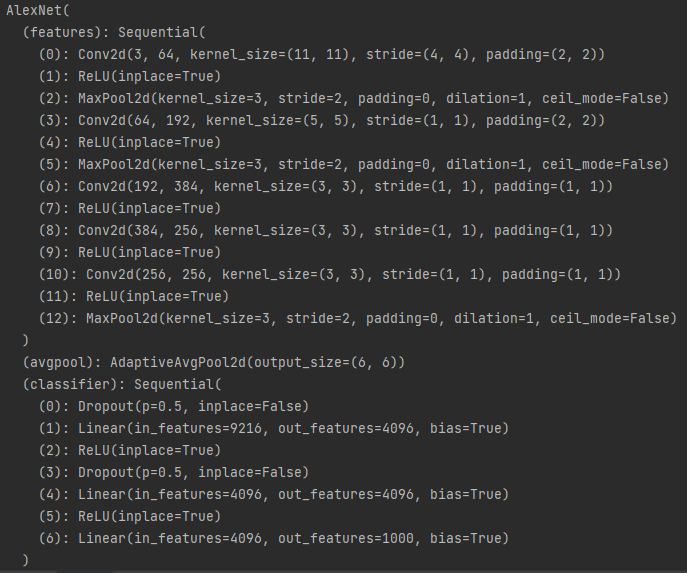
Tips:
- 卷积和线性层后面都加了ReLu
- 池化的k=3,s=2
import torch import torchvision from torch import nn from BasicModule import BasicModule class AlexNet(BasicModule): def __init__(self): super(AlexNet,self).__init__() self.model_name = "AlexNet" self.conv1 = nn.Conv2d(in_channels=1,out_channels=96,kernel_size=11,stride=4,padding=2) self.conv2 = nn.Conv2d(in_channels=96,out_channels=256,kernel_size=5,stride=1,padding=2) self.conv3 = nn.Conv2d(in_channels=256,out_channels=384,kernel_size=3,padding=1) self.conv4 = nn.Conv2d(in_channels=384,out_channels=384,kernel_size=3,padding=1) self.conv5 = nn.Conv2d(in_channels=384, out_channels=256, kernel_size=3,padding=1) self.pool1 = nn.MaxPool2d(kernel_size=3,stride=2) self.pool2 = nn.MaxPool2d(2) self.l1 = nn.Linear(9216,4096) self.l2 = nn.Linear(4096, 4096) self.l3 = nn.Linear(4096, 2) self.drop = nn.Dropout(0.5) def forward(self,x): batch_size = x.size(0) x = self.pool1(nn.ReLU(self.conv1(x))) x = self.pool1(nn.ReLU(self.conv2(x))) x = nn.ReLU(self.conv3(x)) x = nn.ReLU(self.conv4(x)) x = self.pool1(self.conv5(x)) x = x.view(batch_size, -1) x = self.drop(nn.ReLU(self.l1(x))) x = self.drop(nn.ReLU(self.l2(x))) x = self.l3(x) return x model = AlexNet() input = torch.randn(32,1,224,224) output = model(input) print(output.shape)
参考
3. AlexNet


 浙公网安备 33010602011771号
浙公网安备 33010602011771号