OpenCV笔记(9) calcHist绘制直方图
直方图只是简单地将数据归入预定义的组,并在每个组内进行计数。也可以选择对数据提取特征,再对特征进行计数,这里的特征可以是梯度的长度、梯度的方向、颜色或其他任何可以反应数据特点的特征。也就是说,直方图是一种用来揭示数据分布的统计特性的工具。
直方图在计算机视觉中的应用:
- 通过判断帧与帧之间边缘和颜色的统计量是否出现巨大变化,来检测视频中场景的变化。
- 通过使用兴趣点邻域内的特征组成的直方图,来辨识兴趣点。若将边缘、颜色、角点等等的直方图作为特征,可以使用分类器来进行目标识别。
- 提取视频中的颜色或边缘直方图序列,可以用来判断视频是否拷贝自网络。等等。
1 cv::calcHist():从数据创建直方图
函数cv::calcHist()可以从一个或者多个数组中创建直方图。直方图的维度和输入数组的维度或大小无关,而是取决于输入数组的数量。cv::calcHist()总共有三种形式,前两种使用“老式的”C风格数组,第三种使用STLvector模板类型的参数。
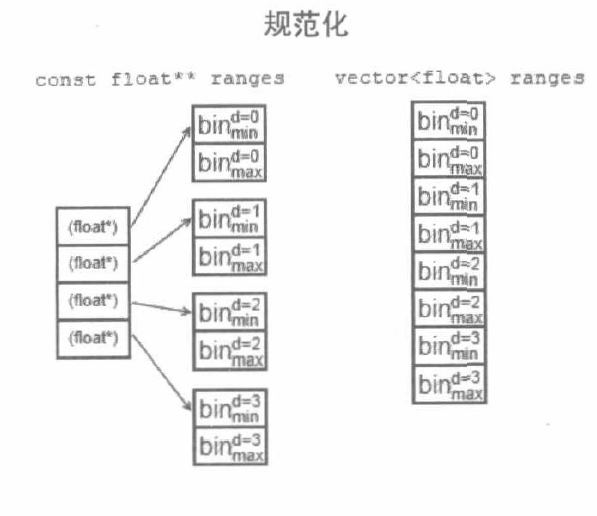
void calcHist( const Mat* images, int nimages,//指向C风格数组列表的指针,同时指定包含的数组个数 const int* channels, InputArray mask,//指定哪些通道要考虑,每个数组哪些像素要考虑 OutputArray hist, int dims, const int* histSize,//直方图计算的输出值,维度,维度中的区间个数 const float** ranges, bool uniform = true, bool accumulate = false );
//区间上下界,区间是否等长,在images得到的数据被累加进hist之前不要将其中的元素删除,重新分配,或置为零
void calcHist( const Mat* images, int nimages, const int* channels, InputArray mask, SparseMat& hist, int dims,//计算结果保存在稀疏矩阵中 const int* histSize, const float** ranges, bool uniform = true, bool accumulate = false );
void calcHist( InputArrayOfArrays images, const std::vector<int>& channels,//channel中的元素个数正是直方图的维度 InputArray mask, OutputArray hist, const std::vector<int>& histSize,//直方图每个维度需要分为多少个区间 const std::vector<float>& ranges,//指定最矮区间的下界,最高区间的上界 bool accumulate = false );
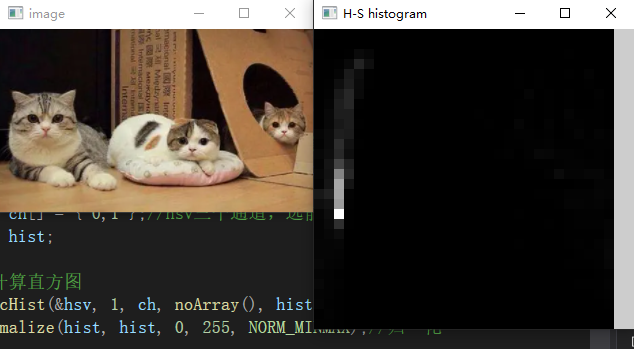
书P339示例13-1:从图片中计算色调(hue)-饱和度(saturation)直方图,然后绘制在网格中
#include <opencv.hpp> using namespace cv; using namespace std; int main() { Mat src = imread("D:\\Backup\\桌面\\a.PNG"); Mat hsv; cvtColor(src, hsv, COLOR_BGR2HSV); float h_ranges[] = { 0,180 };//色调,取值0-180,主要调节颜色 float s_ranges[] = { 0,256 }; //饱和度,取值0 - 255,255饱和度好,0饱和度差 const float* ranges[] = { h_ranges,s_ranges };//两个通道放一起 int histSize[] = { 30,32 };//h,s通道分别取30,32个区间 int ch[] = { 0,1 };//hsv三个通道,选前两个 Mat hist; //计算直方图 calcHist(&hsv, 1, ch, noArray(), hist, 2, histSize, ranges, true); normalize(hist, hist, 0, 255, NORM_MINMAX);//归一化
//画出直方图 int scale = 10;//二维直方图,每个格子10*10 Mat hist_img(histSize[0] * scale, histSize[1] * scale, CV_8UC3);//所需图片尺寸300*320 for (int h = 0; h < histSize[0]; h++) { for (int s = 0; s < histSize[1]; s++) { float hval = hist.at<float>(h, s);//取出hist rectangle(hist_img, Rect(h * scale, s * scale, scale, scale), Scalar::all(hval), -1); } } imshow("image", src); imshow("H-S histogram", hist_img); waitKey(); return 0; }
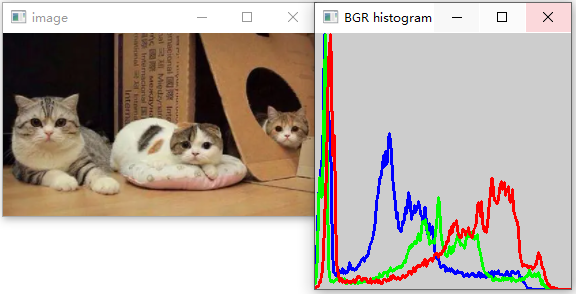
再来一个RGB的
#include <opencv.hpp> using namespace cv; using namespace std; int main() { Mat src = imread("D:\\Backup\\桌面\\a.PNG"); vector<Mat> bgrPlanes; split(src, bgrPlanes); float range[] = { 0,256 }; const float* ranges = { range }; int histSize = 256; vector<Mat> hist(3); vector<Scalar> color = { Scalar(255, 0, 0),Scalar(0, 255, 0),Scalar(0, 0, 255) }; Mat hist_img(histSize, histSize, CV_8UC3);//256*256的图放结果 //计算并绘制直方图 for (int i = 0; i < 3; i++) { calcHist(&bgrPlanes[i], 1, 0, noArray(), hist[i], 1, &histSize, &ranges, true); normalize(hist[i], hist[i], 0, 255, NORM_MINMAX);//归一化 for (int j = 1; j < histSize; j++) { line(hist_img, Point(j - 1, 256 - cvRound(hist[i].at<float>(j - 1))), Point(j, 256 - cvRound(hist[i].at<float>(j))), color[i], 2); } } imshow("image", src); imshow("BGR histogram", hist_img); waitKey(); return 0; }
2 基本直方图操作
2.1 归一化
可以简单使用数组的代数算子和操作来完成直方图归一化:
Mat normalized = my_hist / sum(my_hist)[0];
或者:
void normalize( InputArray src, InputOutputArray dst, double alpha = 1, double beta = 0, int norm_type = NORM_L2, int dtype = -1, InputArray mask = noArray());
void normalize( const SparseMat& src, SparseMat& dst, double alpha, int normType );
示例:
Possible usage with some positive example data: @code{.cpp} vector<double> positiveData = { 2.0, 8.0, 10.0 }; vector<double> normalizedData_l1, normalizedData_l2, normalizedData_inf, normalizedData_minmax; // Norm to probability (total count) // sum(numbers) = 20.0 // 2.0 0.1 (2.0/20.0) // 8.0 0.4 (8.0/20.0) // 10.0 0.5 (10.0/20.0) normalize(positiveData, normalizedData_l1, 1.0, 0.0, NORM_L1); // Norm to unit vector: ||positiveData|| = 1.0 // 2.0 0.15 // 8.0 0.62 // 10.0 0.77 normalize(positiveData, normalizedData_l2, 1.0, 0.0, NORM_L2);//对应L2范数 // Norm to max element // 2.0 0.2 (2.0/10.0) // 8.0 0.8 (8.0/10.0) // 10.0 1.0 (10.0/10.0) normalize(positiveData, normalizedData_inf, 1.0, 0.0, NORM_INF); // Norm to range [0.0;1.0] // 2.0 0.0 (shift to left border) // 8.0 0.75 (6.0/8.0) // 10.0 1.0 (shift to right border) normalize(positiveData, normalizedData_minmax, 1.0, 0.0, NORM_MINMAX); @endcode
2.2 二值化
将直方图二值化,并可以丢弃所有其中元素个数少于个给定值的区间,和归一化相同,二值化也可以不用任何特定的直方图方法来完成。用平时常用的标准数组二值化函数即可:
threshold( my_hist , my_threshold_hist , threshold , 0 , THRESH_TOZERO);//这个0此处没用
2.3 找出最显著的区间
有时你希望能找出所有元素个数高于某个给定阈值的区间,有时你只是希望能找出有最多元素的区间。这种情况多发生在使用直方图来表示概率分布的时候。这时你可以选择使用:
-
cv::minMaxLoc()
void minMaxLoc(InputArray src, double* minVal, double* maxVal = 0, Point* minLoc = 0, Point* maxLoc = 0, InputArray mask = noArray());
如果不需要计算某个结果,只需向其对应的变量传入NULL。如果有一个一维的vector<>数组,则可以使用cv::Mat(vec).reshape(1)来将其转为一个Nx1的二维数组。
稀疏数组的版本:
void minMaxLoc(const SparseMat& a, double* minVal, double* maxVal, int* minIdx = 0, int* maxIdx = 0);
如果是想找出一个n维非稀疏数组中的最大值或是最小值,则需要使用另一个函数:
-
cv::minMaxIdx()
void minMaxIdx(InputArray src, double* minVal, double* maxVal = 0, int* minIdx = 0, int* maxIdx = 0,
InputArray mask = noArray());
如果输入的src是一维的,应该将minIdx,maxIdx置为二维的。 因为函数内部将一维数组视为二维数组。
int max_idx[2]; double max_val; minMaxIdx(hist[0], NULL, &max_val, NULL, max_idx, noArray()); cout << "max_val = " << max_val << "at " << *max_idx;
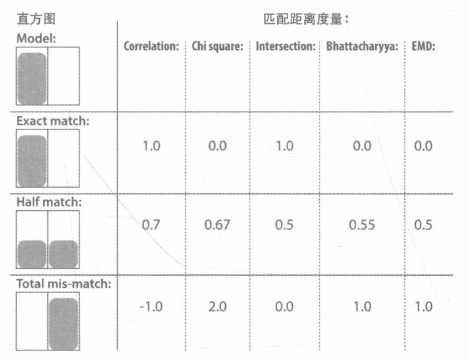
2.4 比较两个直方图 cv::compareHist()
通过特殊的判据对两个直方图的相似度进行度量。
double compareHist( InputArray H1, InputArray H2, int method ); double compareHist( const SparseMat& H1, const SparseMat& H2, int method );
可用的方法如下
- COMP_CORRL 相关性方法
- COMP_CHISQR_ALT 卡方方法,好但慢
- COMP_INTERSECT 交集法,在快速而粗略的匹配中效果很好
- COMP_BHATTACHARYYA 巴氏距离,好但慢
- EMD 最符合直觉的匹配效果,但计算速度更慢
3 复杂的直方图方法
3.1 EMD距离cv::EMD()
光照的变化会使颜色值产生大量的偏移,但这种偏移不改变颜色直方图的形状。核心的困难是对于两个形状相同、但只是相对平移的两个直方图,距离度量会给出一个很大的值。EMD是对平移不敏感的距离度量方法,基本思路是,度量将一部分(或全部)直方图搬到一个新位置要花的功夫。
float EMD( InputArray signature1, InputArray signature2,//以签名的方式传入数组参数 int distType, InputArray cost=noArray(), float* lowerBound = 0, OutputArray flow = noArray() );
首先,在调用函数前必须要将直方图转为签名的形式。签名要求是float类型的数组,每行包括直方图区间的计数值,接下来是该区间的坐标。
参数distType可以是曼哈顿距离(DIST_L1)、欧几里得距离(DIST_L2)、棋盘距离(DIST_C)或自定义距离(DIST_USER)。当使用自定义的距离度量时,用户通过cost参数传进一个(预计算好的)费用矩阵(这时费用矩阵是一个n1xn2的矩阵,n1和n2是signature1和signature2的大小。
参数lowerBound有两个功能(一个是作为输入,另一个是作为输出)。作为返回值时,它是两个直方图重心距离的下界。 为了计算这个下界,必须提供一个标准的距离度量方法(不可以是DIST_USER) ,同时两个签名的总权重必须相同(正如直方图归一化后的情况)。 如果选择提供一个下界,你必须将该值初始化为一个有意义的值。 低于这个下界的,EMD距离才会被计算。例如,如果你想无论何种情况都计算EMD距离,将lowerBound初始化为0即可。
下一个参数flow是一个可选的n1xn2矩阵,用来记录从signature1的第i个点流向 signature2的第j个点的质量。 本质上,这给出的是在计算整个EMD中质量的具体安排情况。
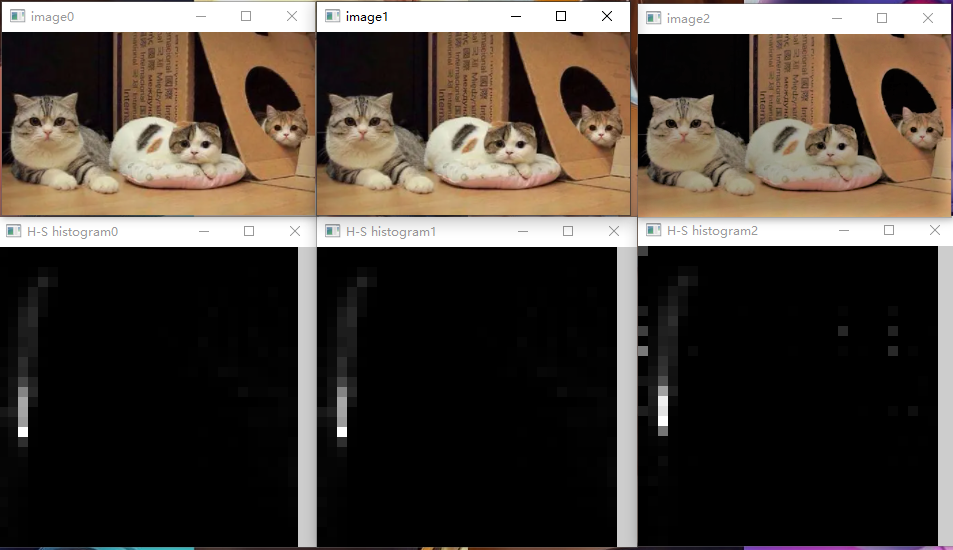
在上文第一个例子色调(hue)-饱和度(saturation)直方图上用EMD方法:
1. 载入多张图:本文用三张图作比较
(image0和image1相同,image2加了滤镜)
2. 创建空签名
vector<Mat> sig(3);
3. 签名要求是float类型的数组,每行包括直方图区间的计数值,接下来是该区间的坐标
vector<Vec3f> sigv;//sigv中的而每一个元素都是,3通道float类型的 Vect(Vec3f) sigv.push_back(Vec3f(hval, (float)h, (float)s)); //在sigv尾部插入
4. 把vector类型的sigv,变为Mat,每一行三个值。注意:局部变量函数结束堆栈会销毁,必须返回堆上的对象,利用clone深拷贝对象。
sig[i] = Mat(sigv).clone().reshape(1);
5. 全代码
#include <opencv.hpp> using namespace cv; using namespace std; int main() { vector<Mat> sig(3); //为calcHist()准备参数 float h_ranges[] = { 0,180 };//色调,取值0-180,主要调节颜色 float s_ranges[] = { 0,256 }; //饱和度,取值0 - 255,255饱和度好,0饱和度差 const float* ranges[] = { h_ranges,s_ranges };//两个通道放一起 int histSize[] = { 30,32 };//h,s通道分别取30,32个区间 int ch[] = { 0,1 };//hsv三个通道,选前两个 //加载三张图,计算三个直方图 vector<Mat> src(3); vector<Mat> hsv(3); vector<Mat> hist(3); for (int i = 0; i < 3; i++) { src[i] = imread("D:\\Backup\\桌面\\"+to_string(i+1)+".PNG"); cvtColor(src[i], hsv[i], COLOR_BGR2HSV); calcHist(&hsv[i], 1, ch, noArray(), hist[i], 2, histSize, ranges, true); normalize(hist[i], hist[i], 0, 255, NORM_MINMAX);//归一化 } //画出三个直方图 int scale = 10;//二维直方图,每个格子10*10 vector<Mat> hist_img(3); for (int i = 0; i < 3; i++) { vector<Vec3f> sigv; hist_img[i] = Mat(histSize[0] * scale, histSize[1] * scale, CV_8UC3); for (int h = 0; h < histSize[0]; h++) { for (int s = 0; s < histSize[1]; s++) { float hval = hist[i].at<float>(h, s); rectangle(hist_img[i], Rect(h * scale, s * scale, scale, scale), Scalar::all(hval), -1); if (hval != 0) sigv.push_back(Vec3f(hval, (float)h, (float)s)); } } sig[i] = Mat(sigv).clone().reshape(1); imshow("image" + to_string(i), src[i]); imshow("H-S histogram" + to_string(i), hist_img[i]); } cout << EMD(sig[0], sig[2], DIST_L2); waitKey(); return 0; }
结果:
EMD(sig[0], sig[1], DIST_L2)=0
EMD(sig[0], sig[2], DIST_L2)=1.94666
3.2 反向投影cv::calcBackProject()
void calcBackProject( const Mat* images, int nimages, const int* channels, InputArray hist, OutputArray backProject, const float** ranges, double scale = 1, bool uniform = true );
void calcBackProject( const Mat* images, int nimages, const int* channels, const SparseMat& hist, OutputArray backProject, const float** ranges, double scale = 1, bool uniform = true );
void calcBackProject( InputArrayOfArrays images, const std::vector<int>& channels, InputArray hist, OutputArray dst, const std::vector<float>& ranges, double scale );
示例:https://blog.csdn.net/keith_bb/article/details/70154219
#include <iostream> #include <opencv2/core.hpp> #include <opencv2/highgui.hpp> #include <opencv2/imgproc.hpp> using namespace std; using namespace cv; //定义全局变量 Mat srcImage, hsvImage, hueImage; const int hueBinMaxValue = 180; int hueBinValue = 25; //声明回调函数 void Hist_and_Backprojection(int, void*); int main() { srcImage = imread("E:\\解条形码\\barcode_new\\crop\\1.bmp"); //判断图像是否加载成功 if (srcImage.empty()) { cout << "图像加载失败" << endl; return -1; } else cout << "图像加载成功..." << endl << endl; //将图像转化为HSV图像 cvtColor(srcImage, hsvImage, CV_BGR2HSV); resize(hsvImage, hsvImage, Size(hsvImage.cols / 20, hsvImage.rows / 20)); //只使用图像的H参数 hueImage.create(hsvImage.size(), hsvImage.depth()); int ch[] = { 0,0 }; mixChannels(&hsvImage, 1, &hueImage, 1, ch, 1); //轨迹条参数设置 char trackBarName[20]; sprintf_s(trackBarName, "Hue bin:%d", hueBinMaxValue); namedWindow("SourceImage", WINDOW_AUTOSIZE); //创建轨迹条并调用回调函数 createTrackbar(trackBarName, "SourceImage", &hueBinValue, hueBinMaxValue, Hist_and_Backprojection); Hist_and_Backprojection(hueBinValue, 0); imshow("SourceImage", srcImage); waitKey(0); return 0; } void Hist_and_Backprojection(int, void*) { MatND hist; int histsize = MAX(hueBinValue, 2); float hue_range[] = { 0,180 }; const float* ranges = { hue_range }; //计算图像直方图并归一化处理 calcHist(&hueImage, 1, 0, Mat(), hist, 1, &histsize, &ranges, true, false); normalize(hist, hist, 0, 255, NORM_MINMAX, -1, Mat()); //获取反向投影 MatND backProjection; calcBackProject(&hueImage, 1, 0, hist, backProjection, &ranges, 1, true); //输出反向投影 imshow("BackProjection", backProjection); //绘制图像直方图 int w = 400; int h = 400; int bin_w = cvRound((double)w / histsize); Mat histImage = Mat::zeros(w, h, CV_8UC3); for (int i = 0; i < hueBinValue; i++) { rectangle(histImage, Point(i * bin_w, h), Point((i + 1) * bin_w, h - cvRound(hist.at<float>(i) * h / 255.0)), Scalar(0, 0, 255), -1); } imshow("HistImage", histImage); }
4 模板匹配cv::matchTemplate()
通过cv::matchTemplate()进行模板匹配并不基于直方图,而是使用一个图像块在输入图像上进行“滑动”,并使用下文要介绍的匹配方法来进行比较。
void matchTemplate( InputArray image, //单字节8位或浮点型灰度或彩色图片
InputArray templ,//一个包含给定物体的(和当前图片相似的)另一张图片上取的图片块。 OutputArray result, //结果存放在result中,它是大小为(image.width-templ.width + 1, image. height -templ.height + 1)的单通道以整数字节或浮点存储的图片。
int method, //匹配方法
InputArray mask = noArray() );
匹配方法:
enum TemplateMatchModes { TM_SQDIFF = 0, //方差匹配法 TM_SQDIFF_NORMED = 1, //归一化方差匹配法 TM_CCORR_NORMED = 3, //归一化互相关匹配法 TM_CCOEFF = 4, //相关系数匹配法 TM_CCOEFF_NORMED = 5 //归一化相关系数匹配法 };
一旦使用cv: :matchTemplate()获得result,我们就可以使用cv: :minMaxloc()或是cv: :minMaxidx()找到最优匹配出现的位置。 同样,为了避免随机性引起的该位置恰好匹配得很好, 我们希望确保在找到的最优匹配的邻域内也有不错的匹配结果。 好的匹配点附近也应该有很好的匹配值, 因为在进行匹配时,对模板位置进行轻微的扰动,并不会引起结果的剧烈变化。你可以在寻找最大匹配值(对于选用相关性判据或是相关系数判据)或者最小值(对于选取方差判据)前,先对结果进行轻微的平滑。 这时,形态学算子可以帮你的忙。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号