[Data]Segment Tree
Segment Tree——线段树
线段树是一种二叉搜索树,它将一个单元划分为几个单元,实际应用是应开4*N空间防止越界。
线段树中的节点可以用来存区间和,区间最小值,最大值都可以。
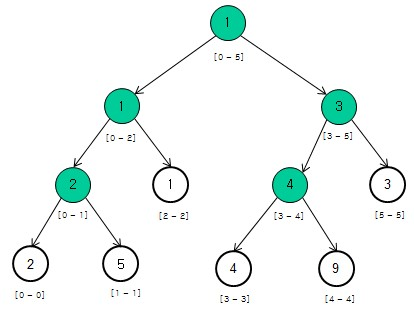
图中的栗子就是对于数组[2,5,1,4,9,3]中维护区间最小值。
当线段树为叶子节点时,它其实就是原数组中的一个元素而已。
为非叶子节点,代表它的所有子树节点所包含的区间的最小值。
由于线段树是平均分割左右子树的,所以它是完全二叉树,对于一棵有n个叶子节点的线段树,
它一定有n-1个非叶子节点,所以它的总节点数为2*n-1。
build——建树
我们用一个数组来存线段树节点,在当前节点,它的左右儿子节点分别为2*n与2*n+1,我们可以从根节点开始,平分左右区间,
递归创建线段树。

void build(int o,int l,int r) { int mid; if(l==r) { tree[o]=a[l]; return; } else { mid=(l+r)/2; dfs(2*o,l,mid); dfs(2*o+1,mid+1,r); tree[o]=tree[o*2]+tree[o*2+1]; } }
query——查询
当我们要查询一个区间的和时(栗子),我们可以把这个区间分散成好几个区间,在当前区间,如果这个区间被要查询的区间完全包含,那么可以直接返回。
如果没有,我们就需判断,它的左右区间与查询区间是否有交集,若有,便递归进入。

void query(int root,int l,int r) { if(l>r) return; if(l>end||r<start) return; if(start<=l&&end>=r) { ans+=tree[root]; return; } push(root,l,r); int mid=(l+r)/2; if(start<=mid) query(root*2,l,mid); if(end>mid) query(root*2+1,mid+1,r); }
单点更新
从根节点更新,判断更新节点所在位置,递归进入左右子节点,但因为更新时它的父节点会产生影响,所以在递归到叶子节点后需回溯更新它的父节点。
区间更新
我们推出了一个叫做“延迟标记"的新产品 ,表明这个点是否需要进行某种修改,若不为0,则需进行修改并下传标记,自己消除标记。
以下是区间每个数加上x。

void push(int root,int l,int r) { int mid=(l+r)/2; if(add[root]!=0) { add[root*2]+=add[root]; add[root*2+1]+=add[root]; tree[root*2]+=add[root]*(mid-l+1); tree[root*2+1]+=add[root]*(r-mid); add[root]=0; } } void update(int root,int l,int r) { if(l>end||r<start) return; if(l>=start&&r<=end) { add[root]+=ad; tree[root]+=ad*(r-l+1); return; } push(root,l,r); int mid=(l+r)/2; update(root*2,l,mid); update(root*2+1,mid+1,r); tree[root]=tree[root*2]+tree[root*2+1]; }
注意!若操作中有要求区间乘某个数,那么注意要先乘后加,因为你先加后乘会使实际数值偏大!

1 void push(int root,int l,int r) 2 { 3 int mid=(l+r)/2; 4 if(aadd[root]!=1) 5 { 6 add[root*2]=aadd[root]*add[root*2]%p; 7 add[root*2+1]=aadd[root]*add[root*2+1]%p; 8 aadd[root*2]=aadd[root]*aadd[root*2]%p; 9 aadd[root*2+1]=aadd[root]*aadd[root*2+1]%p; 10 tree[root*2]=aadd[root]*tree[root*2]%p; 11 tree[root*2+1]=aadd[root]*tree[root*2+1]%p; 12 aadd[root]=1; 13 } 14 if(add[root]!=0) 15 { 16 add[root*2]+=add[root]; 17 add[root*2]%=p; 18 add[root*2+1]+=add[root]; 19 add[root*2+1]%=p; 20 tree[root*2]+=add[root]*(mid-l+1); 21 tree[root*2]%=p; 22 tree[root*2+1]+=add[root]*(r-mid); 23 tree[root*2+1]%=p; 24 add[root]=0; 25 } 26 } 27 long long query(int root,int l,int r) 28 { 29 if(l>end||r<start) 30 return 0; 31 if(start<=l&&end>=r) 32 { 33 return tree[root]; 34 } 35 push(root,l,r); 36 int mid=(l+r)/2; 37 return (query(root*2,l,mid)+query(root*2+1,mid+1,r))%p; 38 }
总代码
luogu 3372

#include<cstdio> #include<algorithm> using namespace std; long long int a[400000]={0},tree[400000]={0},ql,qr,add[400000]={0},end,start,ad,ans=0; void dfs(int o,int l,int r) { int mid; if(l==r) { tree[o]=a[l]; return; } else { mid=(l+r)/2; dfs(2*o,l,mid); dfs(2*o+1,mid+1,r); tree[o]=tree[o*2]+tree[o*2+1]; } } void push(int root,int l,int r) { int mid=(l+r)/2; if(add[root]!=0) { add[root*2]+=add[root]; add[root*2+1]+=add[root]; tree[root*2]+=add[root]*(mid-l+1); tree[root*2+1]+=add[root]*(r-mid); add[root]=0; } } void query(int root,int l,int r) { if(l>r) return; if(l>end||r<start) return; if(start<=l&&end>=r) { ans+=tree[root]; return; } push(root,l,r); int mid=(l+r)/2; if(start<=mid) query(root*2,l,mid); if(end>mid) query(root*2+1,mid+1,r); } void update(int root,int l,int r) { if(l>end||r<start) return; if(l>=start&&r<=end) { add[root]+=ad; tree[root]+=ad*(r-l+1); return; } push(root,l,r); int mid=(l+r)/2; update(root*2,l,mid); update(root*2+1,mid+1,r); tree[root]=tree[root*2]+tree[root*2+1]; } int main() { int n,i,c,s; scanf("%d%d",&n,&c); for(i=1;i<=n;i++) scanf("%lld",&a[i]); dfs(1,1,n); for(i=1;i<=c;i++) { scanf("%d%lld%lld",&s,&start,&end); if(s==1) { scanf("%lld",&ad); update(1,1,n); } else { ans=0; query(1,1,n); //for (int j=1;j<=n*2-1;j++){ // printf("%d %d\n",j,tree[j]); // } printf("%lld\n",ans); } } return 0;}
luogu 3373

#include<cstdio> #include<algorithm> #include<cstring> using namespace std; long long int a[400000]={0},tree[400000]={0},ql,qr,add[400000]={0},end,start,ad, aadd[400000],k,p; void dfs(int o,int l,int r) { aadd[o]=1; add[o]=0; int mid; if(l==r) { tree[o]=a[l]%p; } else { mid=(l+r)/2; dfs(2*o,l,mid); dfs(2*o+1,mid+1,r); tree[o]=(tree[o*2]+tree[o*2+1])%p; } } void push(int root,int l,int r) { int mid=(l+r)/2; if(aadd[root]!=1) { add[root*2]=aadd[root]*add[root*2]%p; add[root*2+1]=aadd[root]*add[root*2+1]%p; aadd[root*2]=aadd[root]*aadd[root*2]%p; aadd[root*2+1]=aadd[root]*aadd[root*2+1]%p; tree[root*2]=aadd[root]*tree[root*2]%p; tree[root*2+1]=aadd[root]*tree[root*2+1]%p; aadd[root]=1; } if(add[root]!=0) { add[root*2]+=add[root]; add[root*2]%=p; add[root*2+1]+=add[root]; add[root*2+1]%=p; tree[root*2]+=add[root]*(mid-l+1); tree[root*2]%=p; tree[root*2+1]+=add[root]*(r-mid); tree[root*2+1]%=p; add[root]=0; } } long long query(int root,int l,int r) { if(l>end||r<start) return 0; if(start<=l&&end>=r) { return tree[root]; } push(root,l,r); int mid=(l+r)/2; return (query(root*2,l,mid)+query(root*2+1,mid+1,r))%p; } void update(int root,int l,int r,int ad) { if(l>end||r<start) return; if(l>=start&&r<=end) { add[root]+=ad; add[root]%=p; tree[root]+=ad*(r-l+1); tree[root]%=p; return; } push(root,l,r); int mid=(l+r)/2; update(root*2,l,mid,ad); update(root*2+1,mid+1,r,ad); tree[root]=(tree[root*2]+tree[root*2+1])%p; } void cheng(int root,int l,int r,int k) { if(l>end||r<start) return; if(l>=start&&r<=end) { add[root]*=k; add[root]%=p; aadd[root]*=k; aadd[root]%=p; tree[root]*=k; tree[root]=tree[root]%p; return; } push(root,l,r); int mid=(l+r)/2; cheng(root*2,l,mid,k); cheng(root*2+1,mid+1,r,k); tree[root]=(tree[root*2]+tree[root*2+1])%p; } int main() { long long int n,i,c,s; scanf("%lld%lld%lld",&n,&c,&p); for(i=1;i<=n;i++) scanf("%lld",&a[i]); dfs(1,1,n); for(i=1;i<=n;i++) aadd[i]=1; for(i=1;i<=c;i++) { scanf("%lld",&s); if(s==1) { scanf("%lld%lld%lld",&start,&end,&k); cheng(1,1,n,k); } if(s==2) { scanf("%lld%lld%lld",&start,&end,&ad); update(1,1,n,ad); } else if(s==3) { scanf("%lld%lld",&start,&end); printf("%lld\n",query(1,1,n)%p); } } return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号