P2495 [SDOI2011] 消耗战 （虚树优化 dp）
2024.11.14
虚树优化 dp 模板题
想出树形 dp 简单。
优化需要注意到无用的转移很多，因为 \(\sum k\) 小，所以如果能将单次 dp 减小到 \(O(k)\) 就可以做了。
想到虚树很好保留了树的必要形态，在这上面 dp 就可以了。
考虑 \(m=1\)。只需要简单的树形 dp，设 \(f_i\) 表示 \(i\) 子树中的关键点都到不了 \(i\) 点的最小代价。转移枚举子节点 \(v\)，有：
若 \(v\) 点为关键点，\(f_u=f_u+w(u,v)\)。
否则，\(f_u=f_u+\min(f_v,w(u,v))\)。
如果每次询问都跑一遍，复杂度 \(O(nm)\)。考虑优化。
我们发现这题最关键的一点是，我们转移时访问的点很多都是无用的。事实上，我们只需要保存关键点以及关键点的 \(lca\) 即可转移。所以我们需要建出一棵新树满足这样的要求。
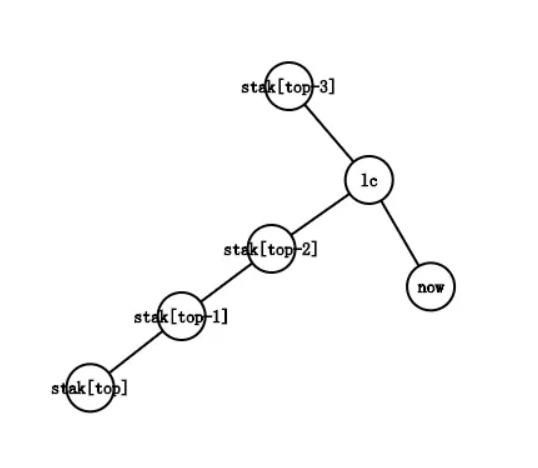
虚树，在原树中保留关键点以及两两的公共祖先和树根所构成的树。如何建出虚树？先将关键点按 \(dfs\) 序从小到大排序。我们考虑不断用栈维护一条最右链，当枚举一个关键点 \(v\) 时，求出 \(rt=lca(s[top],v)\)，有以下情况：
若 \(rt=s[top]\)，说明 \(v\) 在当前最右链上，直接将 \(v\) 插入栈即可。
否则，考虑一直弹栈直到没有点的深度大于 \(rt\)，弹栈的同时连边，最后再插入 \(v\)。这部分细节多，这里只是概述简要思想，具体要用图才能说清楚。下图为一般情况。
到现在，建立虚树的代码呼之欲出。
void build() {
std::sort(a + 1, a + k + 1, cmp); //按 dfs 序排序
st[++top] = 1;
for(int i = 1; i <= k; i++) {
int rt = lca(a[i], st[top]);
while(top && dep[st[top - 1]] >= dep[rt]) {
add(st[top - 1], st[top]), top--;
} //弹栈时连边
if(st[top] != rt) {
add(rt, st[top]), st[top] = rt;
} //特殊情况，rt 为新点，连边后覆盖 st[top]
st[++top] = a[i]; //最后插入 v
}
while(top > 1) {
add(st[top - 1], st[top]);
top--;
} //最后连上最右链
top = 0;
}
在这题里，虚树的边显然是路径上的最小值，倍增预处理即可。
建好虚树后在虚树上跑树形 dp 即可。总复杂度是 \(O(\sum k\log \sum k)=O(n\log n)\)。
#include <bits/stdc++.h>
#define pii std::pair<int, i64>
#define fi first
#define se second
#define pb push_back
typedef long long i64;
const i64 iinf = 0x3f3f3f3f, linf = 0x3f3f3f3f3f3f3f3f;
const int N = 250010;
int n, m, k, tot;
int a[N];
int anc[N][20], dfn[N], dep[N];
i64 mn[N][20];
std::vector<pii> V[N];
void dfs(int u, int fa) {
anc[u][0] = fa;
dfn[u] = ++tot;
dep[u] = dep[fa] + 1;
for(int j = 1; j <= 19; j++) {
anc[u][j] = anc[anc[u][j - 1]][j - 1];
mn[u][j] = std::min(mn[u][j - 1], mn[anc[u][j - 1]][j - 1]);
}
for(auto v : V[u]) {
if(v.fi == fa) continue;
mn[v.fi][0] = v.se;
dfs(v.fi, u);
}
}
int lca(int u, int v) {
if(dep[u] < dep[v]) std::swap(u, v);
for(int i = 19; i >= 0; i--) if(dep[anc[u][i]] >= dep[v]) u = anc[u][i];
if(u == v) return u;
for(int i = 19; i >= 0; i--) if(anc[u][i] != anc[v][i]) u = anc[u][i], v = anc[v][i];
return anc[u][0];
}
int cnt;
int h[N];
struct node {
int to, nxt;
i64 w;
} e[N << 1];
void add(int u, int v, i64 w) {
e[++cnt].to = v, e[cnt].nxt = h[u], e[cnt].w = w;
h[u] = cnt;
}
bool cmp(int a, int b) {
return dfn[a] < dfn[b];
}
i64 calc(int u, int v) {
i64 ret = linf;
for(int i = 19; i >= 0; i--) {
if(dep[anc[u][i]] > dep[v]) ret = std::min(ret, mn[u][i]), u = anc[u][i];
}
return std::min(ret, mn[u][0]);
}
int st[N], top;
void build() {
std::sort(a + 1, a + k + 1, cmp);
st[++top] = 1;
for(int i = 1; i <= k; i++) {
int rt = lca(a[i], st[top]);
while(top && dep[st[top - 1]] >= dep[rt]) {
i64 dis = calc(st[top], st[top - 1]);
add(st[top - 1], st[top], dis), top--;
}
if(st[top] != rt) {
i64 dis = calc(st[top], rt);
add(rt, st[top], dis), st[top] = rt;
}
st[++top] = a[i];
}
while(top > 1) {
i64 dis = calc(st[top], st[top - 1]);
add(st[top - 1], st[top], dis);
top--;
}
top = 0;
}
bool vis[N];
i64 f[N];
void dp(int u, int fa) {
for(int i = h[u]; i; i = e[i].nxt) {
int v = e[i].to; i64 w = e[i].w;
if(v == fa) continue;
dp(v, u);
if(vis[v]) f[u] += w;
else f[u] += std::min(f[v], w);
f[v] = 0, vis[v] = 0;
}
h[u] = 0;
}
void Solve() {
std::cin >> n;
for(int i = 1; i < n; i++) {
int u, v, w;
std::cin >> u >> v >> w;
V[u].pb({v, w}), V[v].pb({u, w});
}
dfs(1, 0);
std::cin >> m;
while(m--) {
std::cin >> k;
for(int i = 1; i <= k; i++) {
std::cin >> a[i];
vis[a[i]] = 1;
}
build();
dp(1, 0);
std::cout << f[1] << "\n"; f[1] = 0;
cnt = 0;
}
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
Solve();
return 0;
}
