P7219 [JOISC2020] 星座 3 (笛卡尔树+整体dp)
2024.11.14
笛卡尔树+整体 dp(线段树合并维护 dp)
能够发现要满足题目条件,只需要考虑到所有极大矩形就可以了。
极大矩形是哪些?因为顶部确定,如果知道底的位置,向左右两端尽可能延伸得到的矩形就是一个极大矩形。
那么一个极大矩形就只会被这段区间(列)的星星影响。要满足条件,也就意味着极大矩形中最多只有一颗星星。
选出的点很少啊,那么让选出的点价值最大就可以了。
最值问题可以考虑 dp,什么样的结构能够刻画这样一个阶段(一个极大矩形就只会被这段区间(列)的星星影响)?实际上就是笛卡尔树。那就在树上 dp 就行了。
每个阶段只需要记录最高的那个星星足够了。转移是子树合并信息的形式。
可以用线段树合并或者启发式合并,一个复杂度小,一个码量小。
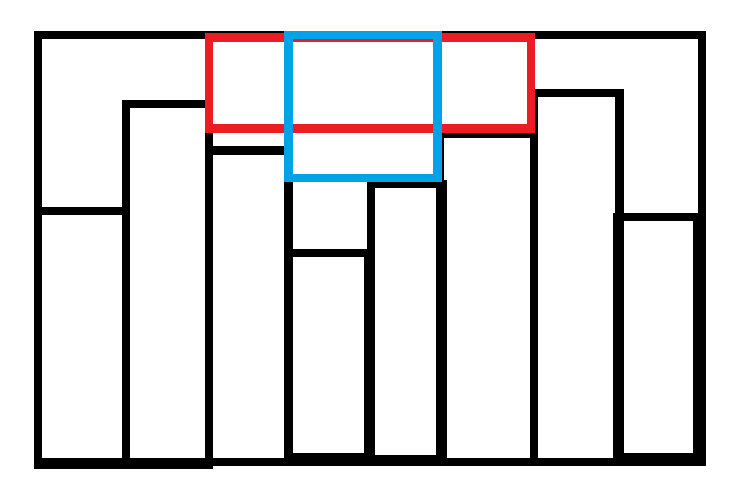
考虑转化题意,不存在矩形为星座,即对于每个极大矩形中都只有一颗星星。而观察题目的方格,对于两个位置是否能够成为一个矩形,只和两个位置的区间最大值(小白船的位置)有关 ①。图中的红蓝矩形即为两个极大矩形。
将删除星星的最小代价改为最多能够取多少点 ②。明显是 dp 的问题,所以看到 ①②,这里有个 trick,建出笛卡尔树,在树上求解。
我们思考在笛卡尔树上求解有什么好处。首先在大根笛卡尔树下,对于每个节点,都对应着一个极大矩形,即以自身高度为底,向左右上延伸的极大矩形。这样在遍历完整棵树后,我们相当于考虑了所有极大矩形。对于每个星星,影响的矩形是树上自叶子结点到某节点的一条链。
考虑树形 dp。观察到转移时只会被最高的星星所影响,设 \(f_{i,j}\) 表示当前在 \(i\) 节点,当前所有选中星星的高度最大值为 \(j\) 的最大权值和。有转移:
当 \(j>a_i\) 时,
星星放在第 \(i\) 列,\(f_{i,j}=f_{ls,k}+f_{rs,k}+v_i(k\le a_i)\)
放在左右两边,\(f_{i,j}=\max(f_{ls,j}+f_{rs,k})(k\le a_i)\) 或 \(f_{i,j}=\max(f_{ls,k}+f_{rs,j})(k\le a_i)\)
当 \(j\le a_i\) 时,
\(f_{i,j}=\max(f_{ls,k}+f_{rs,p})(k,p\le j)\)。
我们发现转移位置都是一段区间,并且直接开是开不下 \(f\) 数组的,可以用动态开点线段树维护。
考虑整体 dp,即线段树合并维护 dp。对于 \(j>a_i\),需要区间询问、单点修改 \(\max\),区间加;对于 \(j\le a_i\),此时每个位置的转移依赖自身,如果考虑每个转移,复杂。可以发现转移一直是前缀最大值,于是只需要用左右子树的最大值修改其中一个位置,保证后面能够转移到即可。
注意线段树合并时不一定要同时转移左右子树,可以一个一个和父亲合并转移,处理好 \(i\) 与左右子树的关系。
复杂度 \(O(n\log n)\)。
#include <bits/stdc++.h>
#define pii std::pair<int, i64>
#define fi first
#define se second
#define pb push_back
typedef long long i64;
const int N = 2e5 + 10;
int n, m, tot;
int a[N], st[N], top;
i64 sum;
std::vector<pii> point[N];
int tr[N][2];
struct seg {
int ls, rs;
i64 mx, lzg;
} t[N * 40];
void pushup(int u, int ls, int rs) {
t[u].mx = std::max(t[ls].mx, t[rs].mx);
}
void gtag(int u, i64 v) {
if(u) t[u].mx += v, t[u].lzg += v;
}
void pd(int u) {
if(!t[u].lzg) return;
gtag(t[u].ls, t[u].lzg), gtag(t[u].rs, t[u].lzg);
t[u].lzg = 0;
}
void ins(int &u, int l, int r, int x, i64 y) {
if(!u) u = ++tot;
if(l == r) {
t[u].mx = std::max(t[u].mx, y);
return;
}
int mid = (l + r) >> 1;
pd(u);
if(x <= mid) ins(t[u].ls, l, mid, x, y);
else ins(t[u].rs, mid + 1, r, x, y);
pushup(u, t[u].ls, t[u].rs);
}
void mdf(int u, int l, int r, int L, int R, i64 x) {
if(L <= l && r <= R) {
gtag(u, x);
return;
}
int mid = (l + r) >> 1;
pd(u);
if(L <= mid) mdf(t[u].ls, l, mid, L, R, x);
if(R > mid) mdf(t[u].rs, mid + 1, r, L, R, x);
pushup(u, t[u].ls, t[u].rs);
}
void mg(int p1, int p2, int l, int r) {
if(l == r) {
t[p1].mx = std::max(t[p1].mx, t[p2].mx);
return;
}
int mid = (l + r) >> 1;
pd(p1), pd(p2);
if(t[p1].ls && t[p2].ls) mg(t[p1].ls, t[p2].ls, l, mid);
else if(t[p2].ls) t[p1].ls = t[p2].ls;
if(t[p1].rs && t[p2].rs) mg(t[p1].rs, t[p2].rs, mid + 1, r);
else if(t[p2].rs) t[p1].rs = t[p2].rs;
pushup(p1, t[p1].ls, t[p1].rs);
}
i64 query(int u, int l, int r, int L, int R) {
if(L <= l && r <= R) {
return t[u].mx;
}
int mid = (l + r) >> 1;
i64 ret = 0;
pd(u);
if(L <= mid) ret = std::max(ret, query(t[u].ls, l, mid, L, R));
if(R > mid) ret = std::max(ret, query(t[u].rs, mid + 1, r, L, R));
return ret;
}
void dp(int u, int v, int h) {
i64 lv = query(u, 1, n, 1, h), rv = query(v, 1, n, 1, h);
mdf(u, 1, n, h + 1, n, rv), mdf(v, 1, n, h + 1, n, lv);
mg(u, v, 1, n);
ins(u, 1, n, h, lv + rv);
}
void dfs(int u) {
for(auto x : point[u]) {
ins(u, 1, n, x.fi, x.se);
}
if(tr[u][0]) dfs(tr[u][0]), dp(u, tr[u][0], a[u]);
if(tr[u][1]) dfs(tr[u][1]), dp(u, tr[u][1], a[u]);
}
void Solve() {
std::cin >> n;
tot = n;
for(int i = 1; i <= n; i++) {
std::cin >> a[i];
int now = top;
while(now && a[st[now]] < a[i]) now--;
if(now) tr[st[now]][1] = i;
if(now < top) tr[i][0] = st[now + 1];
st[++now] = i;
top = now;
}
std::cin >> m;
for(int i = 1; i <= m; i++) {
int x, y;
i64 c;
std::cin >> x >> y >> c;
point[x].pb({y, c});
sum += c;
}
dfs(st[1]);
std::cout << sum - t[st[1]].mx << "\n";
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
Solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号