P8162 [JOI 2022 Final] 让我们赢得选举 （贪心+dp）

P8162 [JOI 2022 Final] 让我们赢得选举

upd 2024.11.14

贪心+dp

看完题目，觉得挺难。随着时间推移，协作者们可能在不同位置，怎么考虑？

如果考虑协作者们一起做事，会不会最优呢？事实证明是会的。所以同一时刻有且只有一个州在演讲。这就简化了思考量。

现在怎么考虑演讲的顺序？一个发现是如果最终获得了若干协作者，那么按 \(B_i\) 从小到大的顺序演讲一定最优。

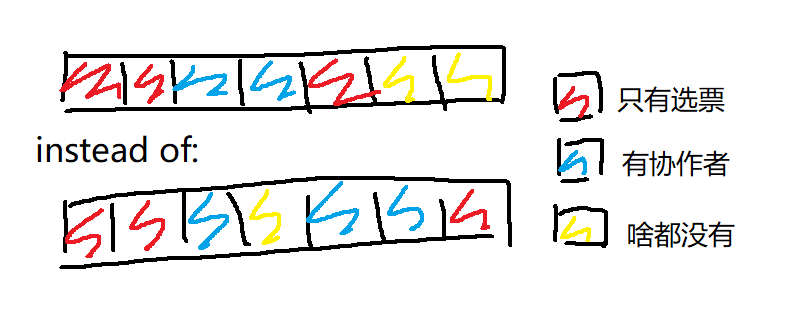
那么我们就可以考虑将序列按照 \(B_i\) 排序，我们的演讲就是从左到右的。现在可以考虑 dp 了吧。设状态 \(f_{i,j,k}\) 表示考虑到前 \(i\) 个州，有 \(j\) 张选票，\(k\) 个协作者的最小耗时。

复杂度太高了，怎么优化？观察协作者的分布，如果一个协作者前面有没有选票的州，那么这位协作者完全可以换成在前面获得。并不影响后面的时间。画个图。

你可以发现前面是一段一定有选票的前缀！那么如果当前只考虑前缀，我们就只需要知道协作者的个数就可以了。

剩下的后面的部分一定是 \(A_i\) 最小的前几个，用个背包也可以求。

题目要求最小耗时，可以考虑贪心和dp。

先考虑贪心。首先，假如我们此时有 \(b\) 个州得到了选票和协作者，那么下一次演讲一定是 \(b\) 个协作者和自己一起去同一个州演讲，时间为 \(\frac{a_i/b_i}{b+1}\)，这样我们的时间一定不会浪费掉。

接下来，若我们已经知道了方案，此时已知每个州是得到选票（\(A\) 类）、得到选票+协作者（\(B\) 类）、不演讲（\(C\) 类）中的一种，我们又可以继续贪心。设有 \(b\) 个 \(B\) 类州，那么我们一定是按从小到大的顺序最先得到所有 \(B\) 类州， \(A\) 类点的答案就是 \(\sum \frac{a_i}{b+1}\)（只受 \(b\) 的影响），这样做时间一定最短。

于是启发我们把序列按 \(b_i\) 从小到大排序，这样在考虑到第 \(i\) 个是 \(B\) 类州时，不会受到后面的影响。接下来可以枚举 \(b\)，对每个 \(b\) 求解。考虑 dp。

设 \(f_{i,j,k}\) 表示考虑到第 \(i\) 个，有 \(j\) 张选票，有 \(k\) 个协作者的最小时间。转移显然。那么 dp 的复杂度是 \(O(n^3)\)，加上枚举的 \(b\)，总复杂度是 \(O(n^4)\)。

考虑优化，继续贪心， 我们两个 \(B\) 类州之间有 \(C\) 类州，那么我们可以把右端的 \(B\) 类州与之间任意 \(C\) 类州互换，这样一定不差。以此类推就有 \(B\) 类州之间不存在 \(C\) 州，且序列最左端也不会有 \(C\) 类州。于是我们可以把序列分成两部分，左部分全是 \(A\) 或 \(B\) 类，右部分一定是 \(A\) 类或 \(C\) 类。如果我们只对左部分 dp，就可以省去 \(j\) 这一维了（因为左部分都有选票）。枚举断点 \(i\)，显然右部分的答案就是 \([i+1,n]\) 中选 \(k-i\) 个 \(a_i\) 的最小和，这个也可以用背包 \(O(n^2)\) 处理。于是每个 \(b\) 的答案就是 \(\min_{i=1}^n(f(i,b)+\frac{g(i+1,k-i)}{b+1})\)。dp 复杂度降到 \(O(n^2)\)，总复杂度是 \(O(n^3)\)。

#include <bits/stdc++.h>
#define pii std::pair<int, int>
#define fi first
#define se second
#define pb push_back

typedef long long i64;
const int N = 510;
int n, k;
struct node {
	int a, b;
} a[N];
bool cmp(node a, node b) {
	return a.b < b.b;
}
double f[N][N], g[N][N];
void Solve() {
	std::cin >> n >> k;

	int B = 0;
	for(int i = 1; i <= n; i++) {
		std::cin >> a[i].a >> a[i].b;
		if(a[i].b != -1) B++;
		a[i].b = ((a[i].b == -1) ? 0x3f3f3f3f : a[i].b);
	}

	std::sort(a + 1, a + n + 1, cmp);
	double ans = 0x3f3f3f3f;
	for(int i = 1; i <= n + 1; i++) {
		for(int j = 1; j <= n + 1; j++) g[i][j] = 600000;
	}
	for(int i = 1; i <= n + 1; i++) g[i][0] = 0;
	for(int i = n; i >= 1; i--) {
		for(int j = 1; j <= n - i + 1; j++) {
			g[i][j] = 600000;
			g[i][j] = std::min(g[i][j], g[i + 1][j]);
			g[i][j] = std::min(g[i][j], g[i + 1][j - 1] + a[i].a);
		}
	}
	for(int b = 0; b <= std::min(B, k); b++) {
		for(int i = 0; i <= n; i++) {
			for(int j = 0; j <= n; j++) f[i][j] = 600000;
		}
		f[0][0] = 0;
		for(int i = 1; i <= k; i++) {
			for(int j = 0; j <= b; j++) {
				f[i][j] = std::min(f[i][j], f[i - 1][j] + (double)(1.0 * a[i].a / (b + 1)));
				if(j - 1 >= 0) f[i][j] = std::min(f[i][j], f[i - 1][j - 1] + (double)(1.0 * a[i].b / j));
			}
		}
		for(int i = b; i <= k; i++) {
			ans = std::min(ans, f[i][b] + (double)(1.0 * g[i + 1][k - i] / (b + 1)));
		}
	}
	printf("%.15lf\n", ans);
}
int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
	Solve();

	return 0;
}