词法分析
词法分析器的任务是按照一定模式从源程序中识别出记号(token).
我们使用正规式描述这一模式,并通过有限自动机进行识别.
正规式与正规集
语言是在有限字母表上有限长字符串的集合.
正规式又称正则表达式, 是一种特殊的字符串用来描述一类的字符串的集合.
我们把可用正规式描述(其结构)的语言称为正规语言或正规集.
在介绍正规式之前, 我们先定义几个字符串集合中的概念:
-
\(\epsilon\): 空串, 没有字符的串不是空格由空格组成的串
-
并运算: $ L \cup M = {s| s \in L or s \in M }$
-
交运算: $ L \cap M = {s| s \in L and s \in M}$
-
连接运算: $ LM = {st | s \in L and t \in M } $ , 任意属于L的字符串与任意属于M的字符串按顺序连接
-
闭包运算: L* $ = L^0 \cup L \cup L^2 $ ..., 其中\(L^0 = {\epsilon}, L^2 = LL\)
-
正闭包: $ L+ = L \cup L^2... $
正规式采用递归定义:
-
\(\epsilon\)是正规式, 表示集合\({\epsilon}\)
-
任意字符a是正规式, 表示集合
-
若r和s是正规式, L(r)和L(s)是它们则:
-
r|s是正规式, 表示的集合为$ L(r) \cup L(s)$
-
rs是正规式, 表示的集合为$ L(r)L(s) $
-
r是正规式, 表示的集合为L(r)
-
r+是正规式, 表示的集合为$ L(r)+ $
-
上面同样定义了正则表达式的基本运算, 运算均为左结合, 优先级从高到低为闭包, 连接, 交并运算,正规式运算可以使用括号改变顺序.
两个正规式描述的集合相同则称它们是等价的, 也就是说正规式和集合之间是多对一的关系.
有限自动机
不确定的有限自动机(Nondeterministic Finite Automaton, NFA)是识别模式的方法, 我们用状态图来描述NFA.
下图的NFA用于识别正规式= < | <= | <> | = | > | >=

NFA的初始状态为0, 若其第一个字符为<则转移到状态1, 其它类推.
若下一个字符为=则转移到状态2并返回, 若下一个字符为>则转移到状态3并返回, 否则直接返回状态1.这里的返回是指以当前状态作为终态, 终止匹配.
上面的策略体现了最长匹配原则, 即达到状态1时不立即返回而是继续尝试状态2或状态3.
NFA识别字符串就是反复试探所有路径,直到到达终态后返回,或者到达不了终态后放弃.一般使用回溯法试探所有路径.
我们使用五个要素描述NFA:
-
状态集S
-
字母表
-
move(i, j)状态转移函数
-
S0初态
-
F终态集
状态转移函数接受两个参数, 当前状态和转移条件, 返回新的状态.
转移条件是指后续字符串满足该条件才会发生状态转移, 比如要求下一个字符为特定字符.
NFA的问题在于:
-
只有尝试了全部可能的路径,才能确定一个输入序列不被接受
-
识别过程中需要进行大量回溯,时间复杂度很高
NFA中对状态转移函数几乎没有限制, 允许其出现一对多的状态转移和\(\epsilon\)状态转移.
所谓\(\epsilon\)状态转移是指转移条件为空, 状态转移可以随意发生, 这种状态转移经常在识别闭包时出现.
确定的有限自动机 (Deterministic Finite Automaton, DFA)是NFA的一个特例,其最大的特点是其状态转移函数都是一对一的且不允许\(\epsilon\)状态转移.
因为NFA对状态转移不加限制在实际应用中带来很多问题, 通常我们将NFA转换为等价的DFA. 这里所谓的自动机等价是指它们识别同样的正规集.
以正规式(a|b)*abb为例, 其NFA可以表示为:
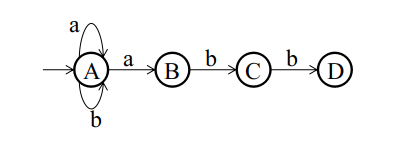
可以看到状态为0, 下一个字符为a时出现一对多的问题.
DFA的状态转移复杂一些:

词法分析器
构建词法分析器一般需要几个步骤:
-
用正规式描述记号的模式
-
为正规式设计NFA
-
将NFA转换为等价的DFA, 这一步称为确定化
-
优化DFA使其状态数最少, 这一步称为最小化
从正规式到NFA
Thompson算法可以用来为一个正规式构建NFA.
-
对\(\epsilon\), 构造NFA:

-
对字符a构造NFA:
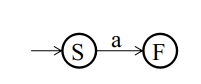
-
r和s是正规式, 它们的NFA为N(r)和N(s):
- r|s的NFA为:

- rs的NFA为:
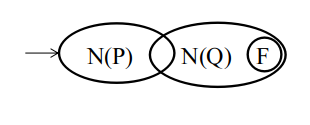
- r*的NFA为:

使用Thompsonn算法构造正规式(a|b)*abb的NFA, 自下而上构建:

作出状态转移图:

从NFA到DFA
基于NFA构造DFA的核心在于将一对多的状态转移确定化.
使用回溯法在发现无法匹配的路径后返回是一种自然的思路, 不过我们可以采用并行的方法.
当发现一对多的情况时我们可以同时试探所有路径, 当发现某条路径不通时直接放弃该路径不必回溯.
\(\epsilon\)闭包
为了消除\(\epsilon\)状态转移, 我们引入\(\epsilon\)闭包的概念:
从状态集T出发,不经任何字符可达到的状态的集合称为T的\(\epsilon\)闭包, 记作\(\epsilon(T)\)
建立一个集合V, 将T添加到V中, 遍历V中的每一个状态s, 将s可以通过\(\epsilon\)状态转移到达的状态添加到V中, 最终得到的V即为T的\(\epsilon\)闭包.
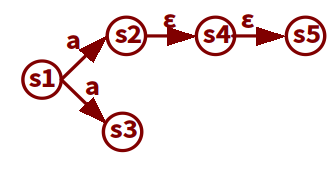
{s2}的\(\epsilon\)闭包为{s2, s4, s5}
为了便于叙述, 我们将从状态集S出发通过条件a可以到达的下一状态全体记作smove(S, a).则$ smove(\epsilon(T), \epsilon) \subset \epsilon(T) $
我们可以把\(\epsilon\)闭包当做一个状态来看待:

在(a|b)*abb的NFA上识别输入序列abb:
-
计算初态集: $ \epsilon({0}) = {0, 1, 2, 4, 7} = A $
-
由A出发经条件a到达: $ \epsilon(smove(A,a)) = {1, 2, 3, 4, 6, 7, 8} = B $
-
由B出发经条件b到达: $ \epsilon(smove(B, b)) = {1, 2, 4, 5, 6, 7, 9} = C $
-
由C出发经条件b到达: $ \epsilon(smove(C, b)) = {1, 2, 4, 5, 6, 7, 10} = D $
-
10为终态,接受
识别abab:
-
计算初态集: $ \epsilon({0}) = {0, 1, 2, 4, 7} = A $
-
由A出发经条件a到达: $ \epsilon(smove(A,a)) = {1, 2, 3, 4, 6, 7, 8} = B $
-
由B出发经条件b到达: $ \epsilon(smove(B, b)) = {1, 2, 4, 5, 6, 7, 9} = C $
-
由C出发经条件a到达: $ \epsilon(smove(C, a)) = {1, 2, 3, 4, 6, 7, 8} = B $
-
由B出发经条件b到达: $ \epsilon(smove(B, b)) = {1, 2, 4, 5, 6, 7, 9} = C $
未到达终态, 不接受
子集构造法
算法流程:
- 初始化数据结构: DFA自动机D, 状态集的集合DS, 状态转义关系集DT
将epsilon({0})加入到DS中, 所有状态置为未标记
当DS中仍有未标记的状态集T时执行循环:
标记T
遍历每一个字符a: // 只有可以从T中转移出去的字符才有意义
令 S = epsilon(smove(T, a))
若S非空:
令DT(T, a) = S
若S不在DS中:
将S作为未标记的状态集加入DS
示例, 由(a|b)*abb的NFA构造DFA:

-
初始化:$ A = \epsilon({0}) = {0, 1, 2, 4, 7}; DS.append(A); $
-
$ B = \epsilon(smove(A, a)) = {1, 2, 3, 4, 6, 7, 8}; DS.append(B); DT(A, a) = B $
-
$ C = \epsilon(smove(A, b)) = {1, 2, 4, 5, 6, 7}; DS.append(C); DT(A, b) = C $
-
$ S = \epsilon(smove(B, a)) = {1, 2, 3, 4, 6, 7, 8}; S == B; DT(B, a) = B $
-
$ D = \epsilon(smove(B, b)) = {1, 2, 3, 4, 6, 7, 8}; DS.append(D); DT(B, b) = D $
-
$ S = \epsilon(smove(C, a)) = {1, 2, 3, 4, 6, 7, 8}; S == B; DT(C, a) = B $
-
$ S = \epsilon(smove(C, b)) = {1, 2, 4, 5, 6, 7}; S == C; DT(C, b) = C $
-
$ S = \epsilon(smove(D, a)) = {1, 2, 3, 4, 6, 7, 8}; S == B; DT(D, a) = B $
-
$ E = \epsilon(smove(D, b)) = {1, 2, 4, 5, 6, 7, 10}; DS.append(E); DT(D, b) = E $
-
$ S = \epsilon(smove(E, a)) = {1, 2, 3, 4, 6, 7, 8}; S == B; DT(E, a) = B $
-
$ S = \epsilon(smove(E, b)) = {1, 2, 4, 5, 6, 7}; S == C; DT(E, b) = C $\
根据DS和DT绘制状态转移图:

最小化DFA
首先引入可区分的概念:对于DFA中任意两个状态s和t, 接受输入字符串w, 若s和t转移到不同状态则称w对于s和t是可区分的.
最小化DFA的目的是使DFA的状态数最少, 定义一个DFA自动机的状态集为S, 终态集为F, 算法流程:
初始化U = {S-F, F}
遍历U中每一个状态集T:
初始化N = U
遍历T中任意状态的组合(s,t, ..):
若对于任意字符a, move(s,a)与move(t,a)均属于U中同一个状态集G:
将s,t划分入同一组, 使用新划分的组代替N中的G
若N == U退出, 以N作为最终划分
令U=N
遍历U中没一个状态集T:
从T中选择一个状态s, 令T中出发的状态转移改为从s出发, 到T的状态转移改为转移到s
清除所有死状态(只能转移到自身且不是终态)和不可达状态.
我们用该算法简化上面的DFA:

-
U =
-
U =
-
U =
AC可合并为一个状态:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号