Space Ant(极角排序)
Space Ant
http://poj.org/problem?id=1696
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 5371 | Accepted: 3343 |
Description
The most exciting space discovery occurred at the end of the 20th century. In 1999, scientists traced down an ant-like creature in the planet Y1999 and called it M11. It has only one eye on the left side of its head and just three feet all on the right side of its body and suffers from three walking limitations:
The pictures transmitted by the Discovery space ship depicts that plants in the Y1999 grow in special points on the planet. Analysis of several thousands of the pictures have resulted in discovering a magic coordinate system governing the grow points of the plants. In this coordinate system with x and y axes, no two plants share the same x or y.
An M11 needs to eat exactly one plant in each day to stay alive. When it eats one plant, it remains there for the rest of the day with no move. Next day, it looks for another plant to go there and eat it. If it can not reach any other plant it dies by the end of the day. Notice that it can reach a plant in any distance.
The problem is to find a path for an M11 to let it live longest.
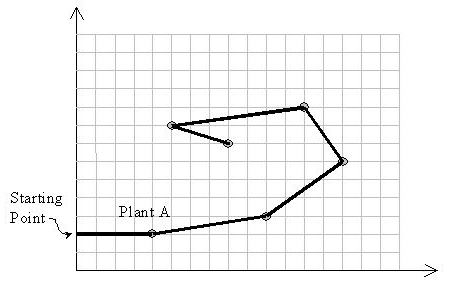
Input is a set of (x, y) coordinates of plants. Suppose A with the coordinates (xA, yA) is the plant with the least y-coordinate. M11 starts from point (0,yA) heading towards plant A. Notice that the solution path should not cross itself and all of the turns should be counter-clockwise. Also note that the solution may visit more than two plants located on a same straight line.
- It can not turn right due to its special body structure.
- It leaves a red path while walking.
- It hates to pass over a previously red colored path, and never does that.
The pictures transmitted by the Discovery space ship depicts that plants in the Y1999 grow in special points on the planet. Analysis of several thousands of the pictures have resulted in discovering a magic coordinate system governing the grow points of the plants. In this coordinate system with x and y axes, no two plants share the same x or y.
An M11 needs to eat exactly one plant in each day to stay alive. When it eats one plant, it remains there for the rest of the day with no move. Next day, it looks for another plant to go there and eat it. If it can not reach any other plant it dies by the end of the day. Notice that it can reach a plant in any distance.
The problem is to find a path for an M11 to let it live longest.
Input is a set of (x, y) coordinates of plants. Suppose A with the coordinates (xA, yA) is the plant with the least y-coordinate. M11 starts from point (0,yA) heading towards plant A. Notice that the solution path should not cross itself and all of the turns should be counter-clockwise. Also note that the solution may visit more than two plants located on a same straight line.

Input
The first line of the input is M, the number of test cases to be solved (1 <= M <= 10). For each test case, the first line is N, the number of plants in that test case (1 <= N <= 50), followed by N lines for each plant data. Each plant data consists of three integers: the first number is the unique plant index (1..N), followed by two positive integers x and y representing the coordinates of the plant. Plants are sorted by the increasing order on their indices in the input file. Suppose that the values of coordinates are at most 100.
Output
Output should have one separate line for the solution of each test case. A solution is the number of plants on the solution path, followed by the indices of visiting plants in the path in the order of their visits.
Sample Input
2 10 1 4 5 2 9 8 3 5 9 4 1 7 5 3 2 6 6 3 7 10 10 8 8 1 9 2 4 10 7 6 14 1 6 11 2 11 9 3 8 7 4 12 8 5 9 20 6 3 2 7 1 6 8 2 13 9 15 1 10 14 17 11 13 19 12 5 18 13 7 3 14 10 16
Sample Output
10 8 7 3 4 9 5 6 2 1 10 14 9 10 11 5 12 8 7 6 13 4 14 1 3 2
找到最左下的点,然后对极角排序即可

1 #include<cstdio> 2 #include<iostream> 3 #include<vector> 4 #include<cstring> 5 #include<algorithm> 6 #include<cmath> 7 using namespace std; 8 const double eps=1e-8; 9 const double INF=1e20; 10 const double PI=acos(-1.0); 11 const int maxp=1010; 12 int sgn(double x){ 13 if(fabs(x)<eps) return 0; 14 if(x<0) return -1; 15 else return 1; 16 } 17 inline double sqr(double x){return x*x;} 18 struct Point{ 19 int pos; 20 double x,y; 21 Point(){} 22 Point(double _x,double _y){ 23 x=_x; 24 y=_y; 25 } 26 void input(){ 27 scanf("%lf %lf",&x,&y); 28 } 29 void output(){ 30 printf("%.2f %.2f\n",x,y); 31 } 32 bool operator == (const Point &b)const{ 33 return sgn(x-b.x) == 0 && sgn(y-b.y)== 0; 34 } 35 bool operator < (const Point &b)const{ 36 return sgn(x-b.x)==0?sgn(y-b.y)<0:x<b.x; 37 } 38 Point operator - (const Point &b)const{ 39 return Point(x-b.x,y-b.y); 40 } 41 //叉积 42 double operator ^ (const Point &b)const{ 43 return x*b.y-y*b.x; 44 } 45 //点积 46 double operator * (const Point &b)const{ 47 return x*b.x+y*b.y; 48 } 49 //返回长度 50 double len(){ 51 return hypot(x,y); 52 } 53 //返回长度的平方 54 double len2(){ 55 return x*x+y*y; 56 } 57 //返回两点的距离 58 double distance(Point p){ 59 return hypot(x-p.x,y-p.y); 60 } 61 Point operator + (const Point &b)const{ 62 return Point(x+b.x,y+b.y); 63 } 64 Point operator * (const double &k)const{ 65 return Point(x*k,y*k); 66 } 67 Point operator / (const double &k)const{ 68 return Point(x/k,y/k); 69 } 70 71 //计算pa和pb的夹角 72 //就是求这个点看a,b所成的夹角 73 ///LightOJ1202 74 double rad(Point a,Point b){ 75 Point p=*this; 76 return fabs(atan2(fabs((a-p)^(b-p)),(a-p)*(b-p))); 77 } 78 //化为长度为r的向量 79 Point trunc(double r){ 80 double l=len(); 81 if(!sgn(l)) return *this; 82 r/=l; 83 return Point(x*r,y*r); 84 } 85 //逆时针转90度 86 Point rotleft(){ 87 return Point(-y,x); 88 } 89 //顺时针转90度 90 Point rotright(){ 91 return Point(y,-x); 92 } 93 //绕着p点逆时针旋转angle 94 Point rotate(Point p,double angle){ 95 Point v=(*this) -p; 96 double c=cos(angle),s=sin(angle); 97 return Point(p.x+v.x*c-v.y*s,p.y+v.x*s+v.y*c); 98 } 99 }; 100 101 struct Line{ 102 Point s,e; 103 Line(){} 104 Line(Point _s,Point _e){ 105 s=_s; 106 e=_e; 107 } 108 bool operator==(Line v){ 109 return (s==v.s)&&(e==v.e); 110 } 111 //根据一个点和倾斜角angle确定直线,0<=angle<pi 112 Line(Point p,double angle){ 113 s=p; 114 if(sgn(angle-PI/2)==0){ 115 e=(s+Point(0,1)); 116 } 117 else{ 118 e=(s+Point(1,tan(angle))); 119 } 120 } 121 //ax+by+c=0; 122 Line(double a,double b,double c){ 123 if(sgn(a)==0){ 124 s=Point(0,-c/b); 125 e=Point(1,-c/b); 126 } 127 else if(sgn(b)==0){ 128 s=Point(-c/a,0); 129 e=Point(-c/a,1); 130 } 131 else{ 132 s=Point(0,-c/b); 133 e=Point(1,(-c-a)/b); 134 } 135 } 136 void input(){ 137 s.input(); 138 e.input(); 139 } 140 void adjust(){ 141 if(e<s) swap(s,e); 142 } 143 //求线段长度 144 double length(){ 145 return s.distance(e); 146 } 147 //返回直线倾斜角 0<=angle<pi 148 double angle(){ 149 double k=atan2(e.y-s.y,e.x-s.x); 150 if(sgn(k)<0) k+=PI; 151 if(sgn(k-PI)==0) k-=PI; 152 return k; 153 } 154 //点和直线的关系 155 //1 在左侧 156 //2 在右侧 157 //3 在直线上 158 int relation(Point p){ 159 int c=sgn((p-s)^(e-s)); 160 if(c<0) return 1; 161 else if(c>0) return 2; 162 else return 3; 163 } 164 //点在线段上的判断 165 bool pointonseg(Point p){ 166 return sgn((p-s)^(e-s))==0&&sgn((p-s)*(p-e))<=0; 167 } 168 //两向量平行(对应直线平行或重合) 169 bool parallel(Line v){ 170 return sgn((e-s)^(v.e-v.s))==0; 171 } 172 //两线段相交判断 173 //2 规范相交 174 //1 非规范相交 175 //0 不相交 176 int segcrossseg(Line v){ 177 int d1=sgn((e-s)^(v.s-s)); 178 int d2=sgn((e-s)^(v.e-s)); 179 int d3=sgn((v.e-v.s)^(s-v.s)); 180 int d4=sgn((v.e-v.s)^(e-v.s)); 181 if((d1^d2)==-2&&(d3^d4)==-2) return 2; 182 return (d1==0&&sgn((v.s-s)*(v.s-e))<=0|| 183 d2==0&&sgn((v.e-s)*(v.e-e))<=0|| 184 d3==0&&sgn((s-v.s)*(s-v.e))<=0|| 185 d4==0&&sgn((e-v.s)*(e-v.e))<=0); 186 } 187 //直线和线段相交判断 188 //-*this line -v seg 189 //2 规范相交 190 //1 非规范相交 191 //0 不相交 192 int linecrossseg(Line v){ 193 int d1=sgn((e-s)^(v.s-s)); 194 int d2=sgn((e-s)^(v.e-s)); 195 if((d1^d2)==-2) return 2; 196 return (d1==0||d2==0); 197 } 198 //两直线关系 199 //0 平行 200 //1 重合 201 //2 相交 202 int linecrossline(Line v){ 203 if((*this).parallel(v)) 204 return v.relation(s)==3; 205 return 2; 206 } 207 //求两直线的交点 208 //要保证两直线不平行或重合 209 Point crosspoint(Line v){ 210 double a1=(v.e-v.s)^(s-v.s); 211 double a2=(v.e-v.s)^(e-v.s); 212 return Point((s.x*a2-e.x*a1)/(a2-a1),(s.y*a2-e.y*a1)/(a2-a1)); 213 } 214 //点到直线的距离 215 double dispointtoline(Point p){ 216 return fabs((p-s)^(e-s))/length(); 217 } 218 //点到线段的距离 219 double dispointtoseg(Point p){ 220 if(sgn((p-s)*(e-s))<0||sgn((p-e)*(s-e))<0) 221 return min(p.distance(s),p.distance(e)); 222 return dispointtoline(p); 223 } 224 //返回线段到线段的距离 225 //前提是两线段不相交,相交距离就是0了 226 double dissegtoseg(Line v){ 227 return min(min(dispointtoseg(v.s),dispointtoseg(v.e)),min(v.dispointtoseg(s),v.dispointtoseg(e))); 228 } 229 //返回点P在直线上的投影 230 Point lineprog(Point p){ 231 return s+(((e-s)*((e-s)*(p-s)))/((e-s).len2())); 232 } 233 //返回点P关于直线的对称点 234 Point symmetrypoint(Point p){ 235 Point q=lineprog(p); 236 return Point(2*q.x-p.x,2*q.y-p.y); 237 } 238 }; 239 240 Line L[100005]; 241 int book[100005]; 242 int n; 243 244 bool Check(Line a,Line b){ 245 if(sgn((a.s-a.e)^(b.s-a.e))*sgn((a.s-a.e)^(b.e-a.e))>0) return false; 246 if(sgn((b.s-b.e)^(a.s-b.e))*sgn((b.s-b.e)^(a.e-b.e))>0) return false; 247 if(sgn(max(a.s.x,a.e.x)-min(b.s.x,b.e.x))>=0&&sgn(max(b.s.x,b.e.x)-min(a.s.x,a.e.x))>=0 248 &&sgn(max(a.s.y,a.e.y)-min(b.s.y,b.e.y))>=0&&sgn(max(b.s.y,b.e.y)-min(a.s.y,a.e.y))>=0) 249 return true; 250 else return false; 251 } 252 253 Point p[105]; 254 int pos; 255 256 double dist(Point a,Point b){ 257 return (b-a)*(b-a); 258 } 259 260 bool cmp(Point a,Point b){ 261 double tmp=(a-p[pos])^(b-p[pos]); 262 if(sgn(tmp)>0){ 263 return true; 264 } 265 else if(sgn(tmp)<0){ 266 return false; 267 } 268 else return dist(p[pos],a)<dist(p[pos],b); 269 } 270 271 int main(){ 272 int T; 273 std::ios::sync_with_stdio(false); 274 cin>>T; 275 while(T--){ 276 int n; 277 cin>>n; 278 pos=1; 279 for(int i=1;i<=n;i++){ 280 cin>>p[i].pos>>p[i].x>>p[i].y; 281 } 282 Point tmp=p[1]; 283 int pp=1; 284 for(int i=2;i<=n;i++){ 285 if((p[i].y<tmp.y)||(p[i].y==tmp.y&&p[i].x<tmp.x)){ 286 tmp=p[i]; 287 pp=i; 288 } 289 } 290 swap(p[pp],p[1]); 291 vector<int>ve; 292 ve.push_back(p[1].pos); 293 for(int i=1;i<n;i++){ 294 sort(p+pos,p+n+1,cmp); 295 pos++; 296 ve.push_back(p[pos].pos); 297 } 298 cout<<n; 299 for(int i=0;i<ve.size();i++){ 300 cout<<" "<<ve[i]; 301 } 302 cout<<endl; 303 } 304 return 0; 305 }
posted on 2018-11-14 21:57 Fighting_sh 阅读(518) 评论(0) 编辑 收藏 举报




